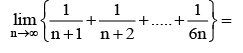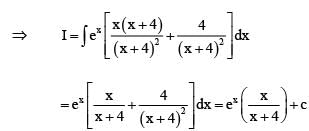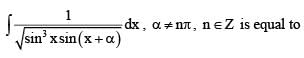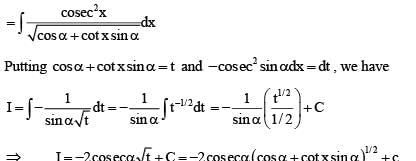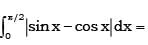All Exams >
JEE >
Chapter-wise Tests for JEE Main & Advanced >
All Questions
All questions of Definite Integrals for JEE Exam
Evaluate: 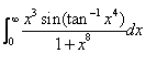
- a)1/2
- b)1/4
- c)1
- d)1/8
Correct answer is option 'B'. Can you explain this answer?
Evaluate: 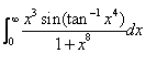
a)
1/2
b)
1/4
c)
1
d)
1/8

|
Sumair Sadiq answered |
This is maths questions I can explain it but you know it is not possible here because this app is not allow to take photo but try it ok let tan inverce 4x =t diff both side wrt x 4x³/1+x⁴ Ka square
x cube / 1+ x8 =dt/4 I = £ 0 se pie by 2 (because when x= 0 t = pie by 2and x = infinity then t = 0 )
I = 1/4 £ 0 se pie by 2 sin t l = 1/4 (- cos t limit 0 se pie by 2 )l = 1/4 ( - cos pie by 2 + cos 0) l = 1/4 ( 0+ 1) l= 1/4 × 1l= 1/4
use my WhatsApp number for further questions but only for study 7060398771
x cube / 1+ x8 =dt/4 I = £ 0 se pie by 2 (because when x= 0 t = pie by 2and x = infinity then t = 0 )
I = 1/4 £ 0 se pie by 2 sin t l = 1/4 (- cos t limit 0 se pie by 2 )l = 1/4 ( - cos pie by 2 + cos 0) l = 1/4 ( 0+ 1) l= 1/4 × 1l= 1/4
use my WhatsApp number for further questions but only for study 7060398771
The value of  is
is- a)0
- b)3/8
- c)4/3
- d)3/4
Correct answer is option 'C'. Can you explain this answer?
The value of  is
is
a)
0
b)
3/8
c)
4/3
d)
3/4
|
|
Poonam Reddy answered |
Since sinq is positive in interval (0, π)
Evaluate as limit of sum 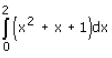
- a)20/5
- b)15/2
- c)20/3
- d)3/20
Correct answer is option 'C'. Can you explain this answer?
Evaluate as limit of sum 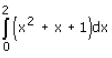
a)
20/5
b)
15/2
c)
20/3
d)
3/20
|
|
Om Desai answered |
∫(0 to 2)(x2 + x + 1)dx
= (0 to 2) [x3/3 + x2/2 + x]½
= [8/3 + 4/2 + 2]
= 40/6
= 20/3
= (0 to 2) [x3/3 + x2/2 + x]½
= [8/3 + 4/2 + 2]
= 40/6
= 20/3
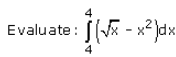
- a)-1
- b)zero
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
a)
-1
b)
zero
c)
1
d)
2

|
Praveen Kumar answered |
∫(0 to 4)(x)1/2 - x2 dx
= [[(x)3/2]/(3/2) - x2](0 to 4)
= [[2x3/2]/3 - x2](0 to 4)
= [[2(0)3/2]/3 - (0)2]] - [[2(4)3/2]/3 - (4)2]]
= 0-0
= 0
= [[(x)3/2]/(3/2) - x2](0 to 4)
= [[2x3/2]/3 - x2](0 to 4)
= [[2(0)3/2]/3 - (0)2]] - [[2(4)3/2]/3 - (4)2]]
= 0-0
= 0
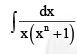 is equal to
is equal to- a)
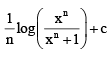
- b)
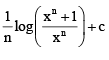
- c)
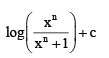
- d)

Correct answer is option 'A'. Can you explain this answer?
a)
b)
c)
d)
|
|
Aryan Khanna answered |
Putting xn = t so that n xn–1 dx = dt
The value of the integral 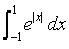 is:
is:- a)2e – 1
- b)2e + 1
- c)2e
- d)2(e – 1)
Correct answer is option 'D'. Can you explain this answer?
The value of the integral 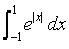 is:
is:
a)
2e – 1
b)
2e + 1
c)
2e
d)
2(e – 1)
|
|
Aryan Khanna answered |
Correct Answer : d
Explanation : ∫(-1 to 1) e|x| dx
∫(-1 to 0) e|x|dx + ∫(0 to 1) e|x|dx
e1 -1 + e1 - 1
=> 2(e - 1)
If 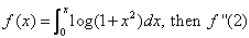 is
is- a)2/3
- b)4/5
- c)1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 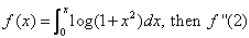 is
is
a)
2/3
b)
4/5
c)
1
d)
None of these
|
|
Om Desai answered |
In the question, it should be f’(2) instead of f”(2)
Explanation:- f(x) = ∫(0 to x) log(1+x2)
f’(x) = 2xdx/(1+x2)
f’(2) = 2(2)/(1+(2)2)
= 4/5
Explanation:- f(x) = ∫(0 to x) log(1+x2)
f’(x) = 2xdx/(1+x2)
f’(2) = 2(2)/(1+(2)2)
= 4/5
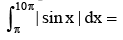
- a)20
- b)8
- c)10
- d)18
Correct answer is option 'D'. Can you explain this answer?
a)
20
b)
8
c)
10
d)
18
|
|
Hardik Handa answered |
Qqqqqqqqqqqqqq
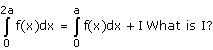
- a)
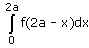
- b)
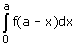
- c)
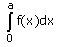
- d)
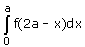
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Vikas Kapoor answered |
Option d is correct, because it is the property of definite integral
∫02a f(x) dx = ∫0a f(x) dx + ∫0a f(2a – x) dx
∫02a f(x) dx = ∫0a f(x) dx + ∫0a f(2a – x) dx

- a)0
- b) π/8
- c)π2/8
- d)π2/16
Correct answer is option 'D'. Can you explain this answer?
a)
0
b)
π/8
c)
π2/8
d)
π2/16
|
|
Gaurav Kumar answered |
By adding (i) and (ii), we get
Now, Put tan2x = t, we get
Find 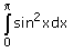
- a)π/4
- b)π/2
- c)4π
- d)2π
Correct answer is option 'B'. Can you explain this answer?
Find 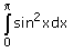
a)
π/4
b)
π/2
c)
4π
d)
2π
|
|
Vivek Patel answered |
Using trigonometric identities, we have
cos2x=cos2x-sin2x -(1) and cos2x+sin2x =1 -(2)
cos2x=1-sin2x , substituting this in equation (1) we get
cos2x=1-sin2x-sin2x=1-2sin2x
So,cos2x=1-2sin2x
2sin2x=1-cos2x
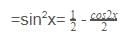
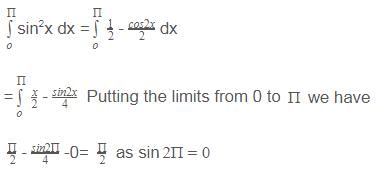
cos2x=cos2x-sin2x -(1) and cos2x+sin2x =1 -(2)
cos2x=1-sin2x , substituting this in equation (1) we get
cos2x=1-sin2x-sin2x=1-2sin2x
So,cos2x=1-2sin2x
2sin2x=1-cos2x
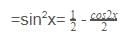
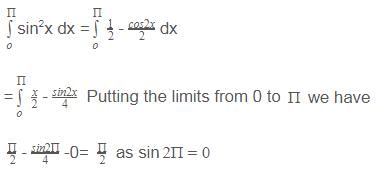
If 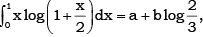 then
then- a)a = 3/2,b=3/2
- b)a = 3/4,b= - 3/4
- c)a = 3/4,b=3/2
- d)a = b
Correct answer is option 'C'. Can you explain this answer?
If 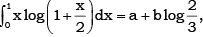 then
then
a)
a = 3/2,b=3/2
b)
a = 3/4,b= - 3/4
c)
a = 3/4,b=3/2
d)
a = b
|
|
Sanjeev Kumar answered |
Integrate it by parts taking log (1+ x/2 )as first function

- a)π/2
- b)0
- c) π/4
- d) π/3
Correct answer is option 'B'. Can you explain this answer?
a)
π/2
b)
0
c)
π/4
d)
π/3
|
|
Gaurav Kumar answered |
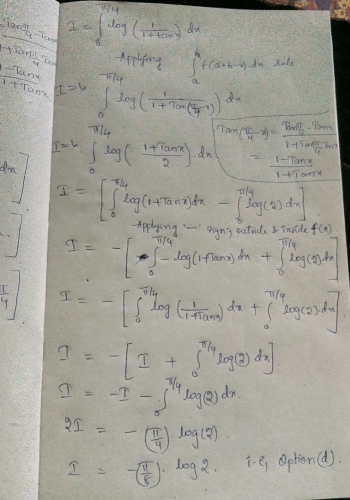
I = ∫0 π2 log(tan x).dx
I = ∫0 π2 log(cot x).dx
Adding both the equations, we get
2I = ∫0 π2 log(tanx) + log(cot x) dx
2I = ∫0 π2 log(1).dx
= 0
I = ∫0 π2 log(cot x).dx
Adding both the equations, we get
2I = ∫0 π2 log(tanx) + log(cot x) dx
2I = ∫0 π2 log(1).dx
= 0
 where [.] denote greatest integer function, is equal to
where [.] denote greatest integer function, is equal to- a)-2
- b)-1
- c)-3
- d)-4
Correct answer is option 'C'. Can you explain this answer?
a)
-2
b)
-1
c)
-3
d)
-4

|
Rishabh Gupta answered |
First we need to divide this integration in two different parts the first part we have to take the limits from - 1 to 0 and in the next part we have to take the integration from 0 to 1 . then in the first part of -1 to 0 just solve for the greatest internet function for -1 to 0 you will get -3 And do the similar thing for 1 to 0 part and you will 0. add -3 and 0 to get your answer.
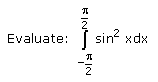
- a)π
- b)π/2
- c)2π
- d)π/4
Correct answer is option 'B'. Can you explain this answer?
a)
π
b)
π/2
c)
2π
d)
π/4

|
Tarun Kaushik answered |
For sin2(X), we will use the cos double angle formula:
cos(2X) = 1 - 2sin2(X)
The above formula can be rearranged to make sin2(X) the subject:
sin2(X) = 1/2(1 - cos(2X))
You can now rewrite the integration:
∫sin2(X)dX = ∫1/2(1 - cos(2X))dX
Because 1/2 is a constant, we can remove it from the integration to make the calculation simpler. We are now integrating:
1/2 x ∫(1 - cos(2X)) dX
= 1/2 x (X - 1/2sin(2X)) + C]-pi/4 to pi/4
∫sin2(X) dX = [1/2X - 1/4sin(2X)]-pi/4 to pi/4 + C
½[-pi/2] - 1/4sin(2(-pi/4)] - ½[pi/2] - 1/4sin(2(pi/4)]
= π/2
cos(2X) = 1 - 2sin2(X)
The above formula can be rearranged to make sin2(X) the subject:
sin2(X) = 1/2(1 - cos(2X))
You can now rewrite the integration:
∫sin2(X)dX = ∫1/2(1 - cos(2X))dX
Because 1/2 is a constant, we can remove it from the integration to make the calculation simpler. We are now integrating:
1/2 x ∫(1 - cos(2X)) dX
= 1/2 x (X - 1/2sin(2X)) + C]-pi/4 to pi/4
∫sin2(X) dX = [1/2X - 1/4sin(2X)]-pi/4 to pi/4 + C
½[-pi/2] - 1/4sin(2(-pi/4)] - ½[pi/2] - 1/4sin(2(pi/4)]
= π/2
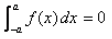
- a)if f(2a – x) = – f(x)
- b)if f(2a – x) = f(x)
- c)if f(- x) = f(x)
- d)if f(- x) = – f(x)
Correct answer is option 'D'. Can you explain this answer?
a)
if f(2a – x) = – f(x)
b)
if f(2a – x) = f(x)
c)
if f(- x) = f(x)
d)
if f(- x) = – f(x)
|
|
Om Desai answered |
∫(-a to a)f(x)dx
= ∫(0 to a) [f(x) + f(-x)] if f(x) is an odd function
⇒ f(-x) = -f(x)
= ∫(0 to a) [f(x) + f(-x)] if f(x) is an odd function
⇒ f(-x) = -f(x)
If  then P =
then P =- a)1/3
- b)1/4
- c)1/2
- d)1/5
Correct answer is option 'C'. Can you explain this answer?
If  then P =
then P =
a)
1/3
b)
1/4
c)
1/2
d)
1/5
|
|
Gaurav Kumar answered |
Comparing it with the given value, we get
The value of integral 
- a)2
- b)- 1
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
The value of integral 
a)
2
b)
- 1
c)
0
d)
1
|
|
Gaurav Kumar answered |
put t = 1/x ⇒ dt = -1/x2 as t = π/2 and π
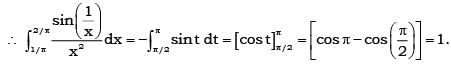
The value of 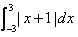 is:
is:- a)10
- b)17/2
- c)7/2
- d)5
Correct answer is option 'A'. Can you explain this answer?
The value of 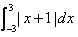 is:
is:
a)
10
b)
17/2
c)
7/2
d)
5

|
Sushil Kumar answered |
∫(-3 to 3) (x+1)dx
= ∫(-3 to -1) (x+1)dx + ∫(-1 to 3) (x+1) dx
= [x2 + x](-3 to -1) + [x2 + x](-1 to 3)
= [½ - 1 - (9/2 - 3)] + [9/2 + 3 - (½ - 1)]
= -[-4 + 2] + [4 + 4]
= -[-2] + [8]
= 10
If 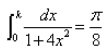 then the value of k is:
then the value of k is:- a)7/8
- b)5/8
- c)1/2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
If 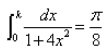 then the value of k is:
then the value of k is:
a)
7/8
b)
5/8
c)
1/2
d)
3/2

|
Sushil Kumar answered |
Let I=∫(0 to k) 1/[1 + 4x2]dx = π8
Now, ∫(0 to k) 1/[4(1/4 + x2)]dx
= 2/4[tan−1 2x]0 to k
= 1/2tan-1 2k − 0 = π/8
1/2tan−1 2k = π8
⇒ tan−1 2k = π/4
⇒ 2k = 1
∴ k = 1/2
Now, ∫(0 to k) 1/[4(1/4 + x2)]dx
= 2/4[tan−1 2x]0 to k
= 1/2tan-1 2k − 0 = π/8
1/2tan−1 2k = π8
⇒ tan−1 2k = π/4
⇒ 2k = 1
∴ k = 1/2
The value of 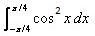 is:
is:- a)
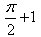
- b)
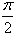
- c)
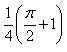
- d)
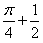
Correct answer is option 'D'. Can you explain this answer?
The value of 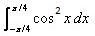 is:
is:
a)
b)
c)
d)
|
|
Samyak Jain answered |
1/2(cos π/2 + 1 -[cos(π/2-π/4)+1])=1/2+π/4
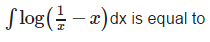
- a)log 2
- b)0
- c)
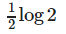
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
a)
log 2
b)
0
c)
d)
none of these

|
Shilpa Saha answered |
∫ log(1-x) dx - ∫ log x dx = 0
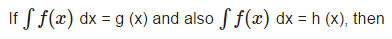
- a)g (x) h (s) = constant
- b)g (x) = h (x).
- c)g (x) - h (x) = constant
- d)h (x) + g (x) = constant
Correct answer is option 'C'. Can you explain this answer?
a)
g (x) h (s) = constant
b)
g (x) = h (x).
c)
g (x) - h (x) = constant
d)
h (x) + g (x) = constant

|
Seblewongel Girma answered |
Integration of a function can have many possibility by adding variable C.
for instance :
take integral of X^2=X^3/3 +C
integral of X^2 can be X^3/3 +1, X^3/3 +2.....
their d/CE is a constant.
for instance :
take integral of X^2=X^3/3 +C
integral of X^2 can be X^3/3 +1, X^3/3 +2.....
their d/CE is a constant.
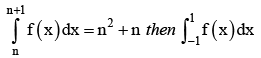
- a)0
- b)-2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
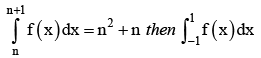
a)
0
b)
-2
c)
3
d)
4
|
|
Anilchoudhary answered |
I DON'T know detail answer but a trick can be applied here
put n = -1 then u get integration from -1 to 0
then put n= 0 you get answer from 0 to 1 then add both its a property of integration .
Find the distance travelled by a car moving with acceleration given by a(t)=Sin(t), if it moves from t = 0 sec to t = π/2 sec, if velocity of a car at t=0sec is 10 km/hr.- a)10.19 km
- b)19.13 km
- c)15.13 km
- d)13.13 km
Correct answer is option 'D'. Can you explain this answer?
Find the distance travelled by a car moving with acceleration given by a(t)=Sin(t), if it moves from t = 0 sec to t = π/2 sec, if velocity of a car at t=0sec is 10 km/hr.
a)
10.19 km
b)
19.13 km
c)
15.13 km
d)
13.13 km

|
Rohit Yadav answered |
Add constant automatically
We know that,
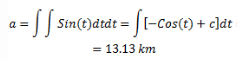
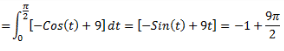
We know that,
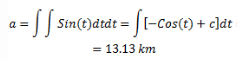
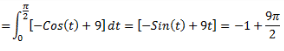
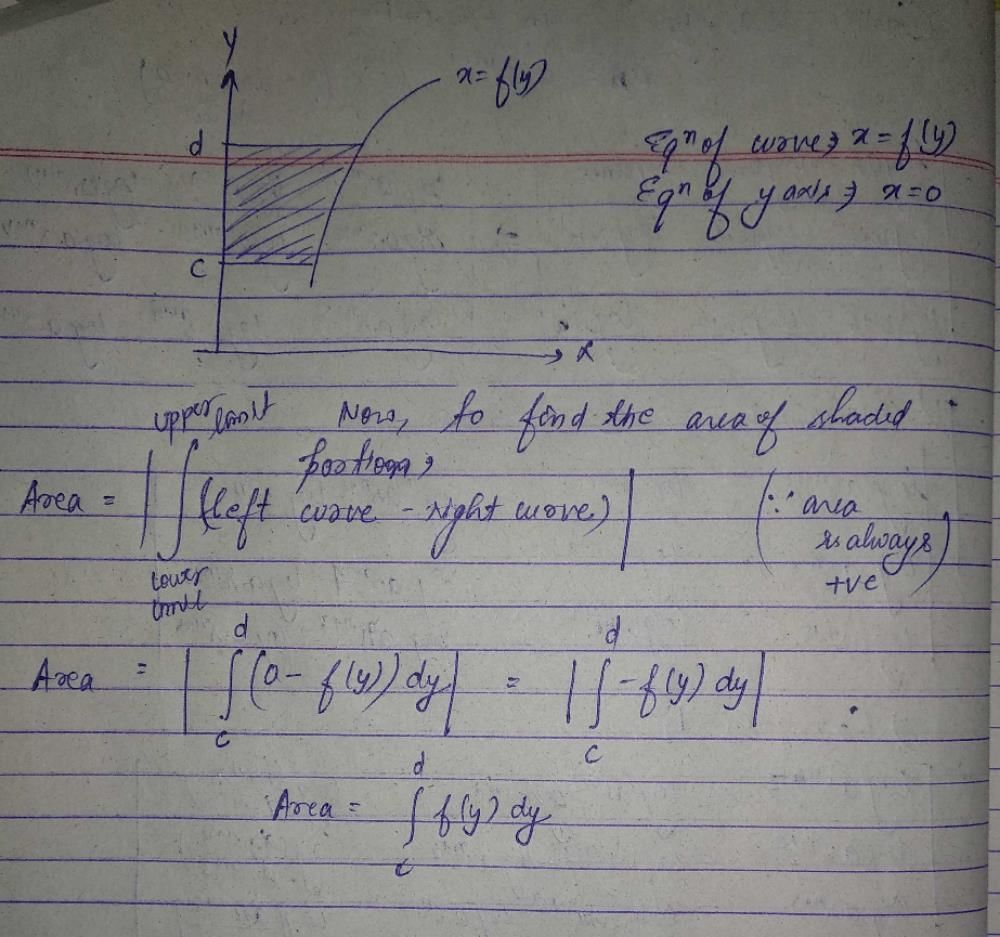
In 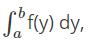 dy, what is ‘a’ called as?
dy, what is ‘a’ called as?
- a)Integration
- b)Upper limit
- c)Lower limit
- d)Limit of an integral
Correct answer is option 'C'. Can you explain this answer?
In 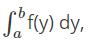 dy, what is ‘a’ called as?
dy, what is ‘a’ called as?
a)
Integration
b)
Upper limit
c)
Lower limit
d)
Limit of an integral
|
|
Anjali Sharma answered |
In 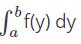 dy ‘a’ is the called as lower limit and ‘b’ is called the upper limit of the integral. The function f in
dy ‘a’ is the called as lower limit and ‘b’ is called the upper limit of the integral. The function f in 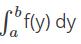 is called the integrand. The letter ‘y’ is a dummy symbol and can be replaced by any other symbol.
is called the integrand. The letter ‘y’ is a dummy symbol and can be replaced by any other symbol.
Chapter doubts & questions for Definite Integrals - Chapter-wise Tests for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Definite Integrals - Chapter-wise Tests for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup