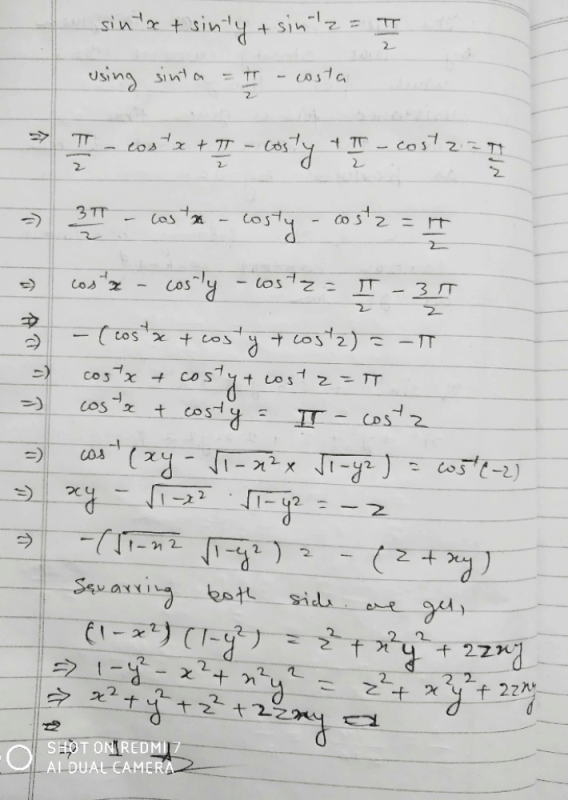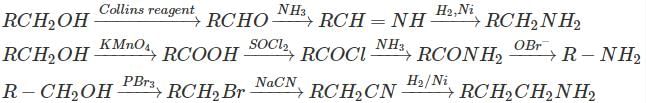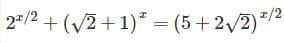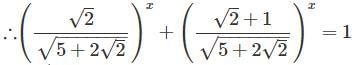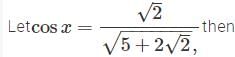All Exams >
JEE >
Mock Tests for JEE Main and Advanced 2026 >
All Questions
All questions of JEE Main Practice Tests for JEE Exam
The average degree of freedom per molecule of a gas is 6. The gas performs 25 J work, while expanding at constant pressure. The heat absorbed by the gas is:-- a)75 J
- b)100 J
- c)150 J
- d)125 J
Correct answer is option 'B'. Can you explain this answer?
The average degree of freedom per molecule of a gas is 6. The gas performs 25 J work, while expanding at constant pressure. The heat absorbed by the gas is:-
a)
75 J
b)
100 J
c)
150 J
d)
125 J
|
|
Rohit Jain answered |
Change in the internal energy of gas is
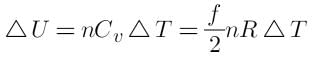
For a constant pressure process. Work done (W) = nRΔT
So heat absorbed by the gas is
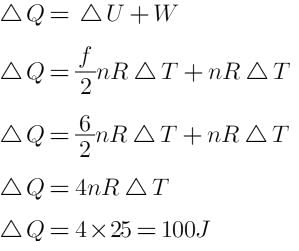
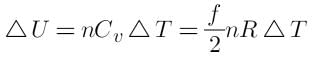
For a constant pressure process. Work done (W) = nRΔT
So heat absorbed by the gas is
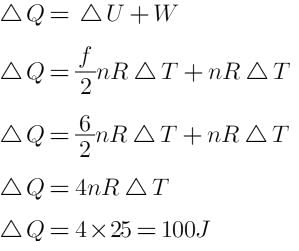
If sin 5x + sin 3 x + sin x = 0, then the value of x other than zero, lying between 0 < x < π/2 is- a)π/6
- b)π/12
- c)π/3
- d)π/4
Correct answer is option 'C'. Can you explain this answer?
If sin 5x + sin 3 x + sin x = 0, then the value of x other than zero, lying between 0 < x < π/2 is
a)
π/6
b)
π/12
c)
π/3
d)
π/4
|
|
Yash Patel answered |
1. sin 5x + sin x + sin 3x = 0
2 sin 3x . cos2x + sin3x = 0
sin 3x (2 cos 2x + 1) = 0, 0 ≤ x ≤π/2
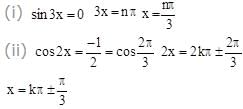
From both x = π / 3 (other than 0).
2 sin 3x . cos2x + sin3x = 0
sin 3x (2 cos 2x + 1) = 0, 0 ≤ x ≤π/2
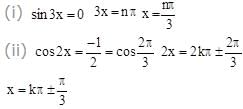
From both x = π / 3 (other than 0).
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is- a)t
- b)4t
- c)2t
- d)t/4
Correct answer is option 'C'. Can you explain this answer?
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is
a)
t
b)
4t
c)
2t
d)
t/4

|
Amit Yadav answered |
B
In the given figure a ring of mass m is kept on a horizontal surface while a body of equal mass 'm' attached through a string, which is wounded on the ring. When the system is released the ring rolls without slipping. Consider the following statements and choose the correct option.
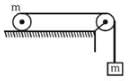
(i) acceleration of the centre of mass of ring is g/3
(ii) acceleration of the hanging particle is 2g/3
(iii) frictional force (on the ring) acts along forward direction
(iv) frictional force (on the ring) acts along backward direction- a)statement (i) and (ii) only
- b)statement (ii) and (iii) only
- c)statement (iii) and (iv) only
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
In the given figure a ring of mass m is kept on a horizontal surface while a body of equal mass 'm' attached through a string, which is wounded on the ring. When the system is released the ring rolls without slipping. Consider the following statements and choose the correct option.

(i) acceleration of the centre of mass of ring is g/3
(ii) acceleration of the hanging particle is 2g/3
(iii) frictional force (on the ring) acts along forward direction
(iv) frictional force (on the ring) acts along backward direction

(i) acceleration of the centre of mass of ring is g/3
(ii) acceleration of the hanging particle is 2g/3
(iii) frictional force (on the ring) acts along forward direction
(iv) frictional force (on the ring) acts along backward direction
a)
statement (i) and (ii) only
b)
statement (ii) and (iii) only
c)
statement (iii) and (iv) only
d)
none of these

|
Cstoppers Instructors answered |
Free body diagram of ring and mass is
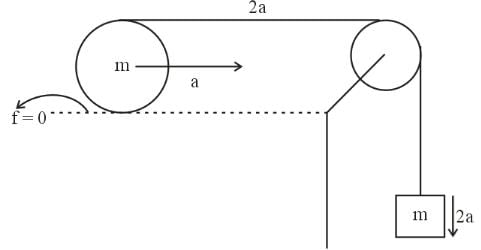
Since the ring is in pure rolling so its above point acceleration will be 2a and similarly acceleration of mass will be 2a.
The equation of motion of the system is
mg – T = m(2a) ......(1)
T = ma .......(2)
Substitute the value of T in equation (1)
mg - ma = 2ma
3ma = mg
a = g/3
So the acceleration of the center of the ring is, g/3
And acceleration of the hanging mass is 2a = 2g/3

Since the ring is in pure rolling so its above point acceleration will be 2a and similarly acceleration of mass will be 2a.
The equation of motion of the system is
mg – T = m(2a) ......(1)
T = ma .......(2)
Substitute the value of T in equation (1)
mg - ma = 2ma
3ma = mg
a = g/3
So the acceleration of the center of the ring is, g/3
And acceleration of the hanging mass is 2a = 2g/3
Two spherical bodies of mass M and 5 M and radii R and 2 R, respectively are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is- a)2.5 R
- b)4.5 R
- c)7.5 R
- d)1.5 R
Correct answer is option 'C'. Can you explain this answer?
Two spherical bodies of mass M and 5 M and radii R and 2 R, respectively are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is
a)
2.5 R
b)
4.5 R
c)
7.5 R
d)
1.5 R

|
Dipanjan Majumdar answered |
Let at O, a collision. If small sphere moves x distance and Big sphere moves (9R - c) distance.

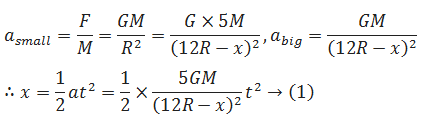
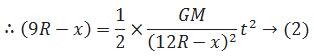
Divide eq (1) by eq (2)
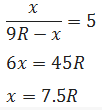
If the pairs of straight lines x2 - 2pxy - y2 = 0 and x2 - 2qxy - y2 = 0 be such that each pair bisects the angle between the other pair, then pq is equal to
Correct answer is '-1'. Can you explain this answer?
If the pairs of straight lines x2 - 2pxy - y2 = 0 and x2 - 2qxy - y2 = 0 be such that each pair bisects the angle between the other pair, then pq is equal to
|
|
Raghav Bansal answered |
Given equations are
x2 - 2qxy - y2 = 0 ... (1)
x2 - 2pxy - y2 = 0 ... (2)
Joint equations of angle bisector of the lines (i) and (ii) are same.
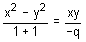
qx2 + 2xy - qy2 = 0 ... (3)
Now, (2) and (3) are same.
Taking ratio of their coefficients.
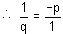
⇒ pq = -1
A shell is fired from a cannon with a speed of 100 ms-1 at an angle 30° with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1 : 2. The lighter fragment moves vertically upwards with an initial speed of 200 ms-1. What is the speed of the heavier fragment at the time of explosion?
- a)125 ms-1
- b)150 ms-1
- c)175 ms-1
- d)200 ms-1
Correct answer is option 'A'. Can you explain this answer?
A shell is fired from a cannon with a speed of 100 ms-1 at an angle 30° with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1 : 2. The lighter fragment moves vertically upwards with an initial speed of 200 ms-1. What is the speed of the heavier fragment at the time of explosion?
a)
125 ms-1
b)
150 ms-1
c)
175 ms-1
d)
200 ms-1
|
|
Ritu Singh answered |
Let's first find the initial velocities of the shell in the x and y directions.
v0x = v0 * cos(60�) = 100 * cos(60�) = 50 ms^(-1)
v0y = v0 * sin(60�) = 100 * sin(60�) = 86.60 ms^(-1)
Now, let's find the time it takes for the shell to reach the highest point of its trajectory. At the highest point, the vertical velocity will be zero. We can use the following equation:
v = u + at
0 = 86.60 - 9.81t
t = 8.83 s
Now we can find the horizontal distance traveled by the shell at the highest point:
x = v0x * t = 50 * 8.83 = 441.5 m
Next, we can find the total momentum of the shell just before the explosion. Since there is no external force in the horizontal direction, the horizontal momentum is conserved.
Momentum_before = Momentum_after
Let m1 be the mass of the lighter fragment and m2 be the mass of the heavier fragment (m2 = 2m1). The velocity of the lighter fragment after the explosion is given as 200 ms^(-1) in the vertical direction. The heavier fragment will have some velocity in both the x and y directions. Let's call these velocities v2x and v2y.
The initial momentum of the shell in the x direction is (m1 + m2) * v0x. Since there is no external force in the x direction, the momentum in the x direction is conserved. Thus:
(m1 + m2) * v0x = m1 * 0 + m2 * v2x
(m1 + m2) * 50 = 2m1 * v2x
In the y direction, the initial momentum of the shell is (m1 + m2) * 0 (because the shell is momentarily at rest at the highest point). Thus:
0 = m1 * 200 - m2 * v2y
0 = 200m1 - 2m1 * v2y
Now we have two equations and two unknowns, v2x and v2y. We can solve these equations simultaneously.
Divide the x-direction equation by 2m1:
50 = v2x
Now substitute this value into the y-direction equation:
0 = 200 - 2 * v2y
v2y = 100 ms^(-1)
Now, we can find the magnitude of the velocity of the heavier fragment (v2) using the Pythagorean theorem:
v2 = sqrt(v2x^2 + v2y^2) = sqrt(50^2 + 100^2) = 125 ms^(-1)
So the speed of the heavier fragment at the time of explosion is 125 ms^(-1). The correct answer is (a) 125 ms^(-1).
v0x = v0 * cos(60�) = 100 * cos(60�) = 50 ms^(-1)
v0y = v0 * sin(60�) = 100 * sin(60�) = 86.60 ms^(-1)
Now, let's find the time it takes for the shell to reach the highest point of its trajectory. At the highest point, the vertical velocity will be zero. We can use the following equation:
v = u + at
0 = 86.60 - 9.81t
t = 8.83 s
Now we can find the horizontal distance traveled by the shell at the highest point:
x = v0x * t = 50 * 8.83 = 441.5 m
Next, we can find the total momentum of the shell just before the explosion. Since there is no external force in the horizontal direction, the horizontal momentum is conserved.
Momentum_before = Momentum_after
Let m1 be the mass of the lighter fragment and m2 be the mass of the heavier fragment (m2 = 2m1). The velocity of the lighter fragment after the explosion is given as 200 ms^(-1) in the vertical direction. The heavier fragment will have some velocity in both the x and y directions. Let's call these velocities v2x and v2y.
The initial momentum of the shell in the x direction is (m1 + m2) * v0x. Since there is no external force in the x direction, the momentum in the x direction is conserved. Thus:
(m1 + m2) * v0x = m1 * 0 + m2 * v2x
(m1 + m2) * 50 = 2m1 * v2x
In the y direction, the initial momentum of the shell is (m1 + m2) * 0 (because the shell is momentarily at rest at the highest point). Thus:
0 = m1 * 200 - m2 * v2y
0 = 200m1 - 2m1 * v2y
Now we have two equations and two unknowns, v2x and v2y. We can solve these equations simultaneously.
Divide the x-direction equation by 2m1:
50 = v2x
Now substitute this value into the y-direction equation:
0 = 200 - 2 * v2y
v2y = 100 ms^(-1)
Now, we can find the magnitude of the velocity of the heavier fragment (v2) using the Pythagorean theorem:
v2 = sqrt(v2x^2 + v2y^2) = sqrt(50^2 + 100^2) = 125 ms^(-1)
So the speed of the heavier fragment at the time of explosion is 125 ms^(-1). The correct answer is (a) 125 ms^(-1).
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is p/q, then p is equal to
Correct answer is '2'. Can you explain this answer?
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is p/q, then p is equal to

|
Learners Habitat answered |
Number of horses = 5
∴ Probability that 'A' cannot win the race 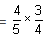
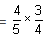
Probability that 'A' must win the race = 1 - Probability that 'A' cannot win the race
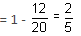
Directions: The answer to this question is a single-digit integer, ranging from 0 to 9. Enter the correct digit in the box given below. Q. A 40 cm diameter pipe branches into two pipes of diameters 10 cm and 20 cm each. If the average velocities of water that flows through 10 cm and 20 cm pipes are 6 m/s and 2 m/s, respectively, then the speed of the water that flows through the 40 cm pipe (in m/s) is (Answer up to nearest integer)
Correct answer is '1'. Can you explain this answer?

|
Rohan Chakraborty answered |
Volume flow = Area of cross-section x average speed

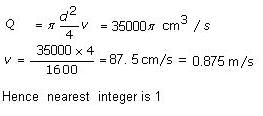
If the binding energy of an electron in a hydrogen atom is 13.6 eV, then the energy required to remove the electron from the first excited state of Li++ is- a)30.6 eV
- b)13.6 eV
- c)3.4 eV
- d)122.4 eV
Correct answer is option 'A'. Can you explain this answer?
If the binding energy of an electron in a hydrogen atom is 13.6 eV, then the energy required to remove the electron from the first excited state of Li++ is
a)
30.6 eV
b)
13.6 eV
c)
3.4 eV
d)
122.4 eV
|
|
Krishna Iyer answered |
Binding energy of the electron,
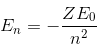
Hence, for n = 2:
Binding energy, E2 = 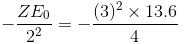
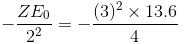
E2 = -30.6 eV
Energy required to remove the electron from the first excited state of Li++ = 30.6 eV
Arrhenius relation is described as K= A e-Ea/RT which of the following statement is correct regarding activation energy- a)Lower activation energy reactions are more susceptible to temperature change
- b)Higher activation energy reactions are more susceptible to temperature change
- c)Activation energy is thermo dynamical concept while rate is kinetic concept both are fundamentally different
- d)Activation energy is of reaction is independent from temperature.
Correct answer is option 'B'. Can you explain this answer?
Arrhenius relation is described as K= A e-Ea/RT which of the following statement is correct regarding activation energy
a)
Lower activation energy reactions are more susceptible to temperature change
b)
Higher activation energy reactions are more susceptible to temperature change
c)
Activation energy is thermo dynamical concept while rate is kinetic concept both are fundamentally different
d)
Activation energy is of reaction is independent from temperature.

|
Avi Chawla answered |
K= 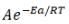
Differentiating with respect to T
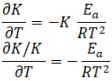
Here we can see that on increasing temperature those reaction having high value of Ea will be more susceptible to change in rate.
Hence, option (b) is correct.
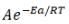
Differentiating with respect to T
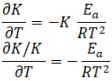
Here we can see that on increasing temperature those reaction having high value of Ea will be more susceptible to change in rate.
Hence, option (b) is correct.
The number of values of a for which the pair of lines represented by 3ax2 + 5xy + (a2 - 2)y2 = 0, perpendicular to each other, is
Correct answer is '2'. Can you explain this answer?
The number of values of a for which the pair of lines represented by 3ax2 + 5xy + (a2 - 2)y2 = 0, perpendicular to each other, is
|
|
Neha Pillai answered |
Perpendicular Lines:
In order to determine the number of values of 'a' for which the pair of lines represented by the given equation are perpendicular, we need to understand the conditions for two lines to be perpendicular.
Two lines are perpendicular if the product of their slopes is -1. The slope of a line is given by the coefficient of x divided by the coefficient of y in the equation of the line.
Equation Analysis:
The given equation is: 3ax^2 + 5xy + (a^2 - 2)y^2 = 0
To find the slopes of the lines represented by this equation, we need to convert it into the standard form of a line equation, which is in the form of ax + by + c = 0.
Converting the Equation:
Let's convert the given equation into the standard form by rearranging the terms:
3ax^2 + 5xy + (a^2 - 2)y^2 = 0
3ax^2 + 5xy + a^2y^2 - 2y^2 = 0
3ax^2 + 5xy + a^2y^2 = 2y^2
Now, let's divide the entire equation by y^2 to get rid of the quadratic terms:
(3ax^2 + 5xy + a^2y^2) / y^2 = 2y^2 / y^2
3ax^2 / y^2 + 5xy / y^2 + a^2 = 2
Simplifying further:
3a(x/y)^2 + 5(x/y) + a^2 = 2
Now, let's consider x/y as a new variable, say 'm':
3am^2 + 5m + a^2 - 2 = 0
Conditions for Perpendicular Lines:
For two lines to be perpendicular, the product of their slopes should be -1. Therefore, we need to find the values of 'a' for which the slopes of the lines represented by the given equation satisfy this condition.
Calculating the Slopes:
The slope of the line represented by the given equation can be found by differentiating the equation with respect to x/y and solving for m.
Differentiating the equation 3am^2 + 5m + a^2 - 2 = 0 with respect to m:
6am + 5 = 0
m = -5/6a
Product of Slopes:
Now, let's find the product of the slopes of the two lines represented by the given equation:
m1 * m2 = (-5/6a) * (-5/6a) = 25/36a^2
Condition for Perpendicular Lines:
To find the values of 'a' for which the lines are perpendicular, we need the product of their slopes to be -1.
Therefore, 25/36a^2 = -1
36a^2 = -25
a^2 = -25/36
Solution:
The equation a^2 = -25/36 has no real solutions since the square of a real number cannot be negative.
Therefore, there are no values of 'a' for which
In order to determine the number of values of 'a' for which the pair of lines represented by the given equation are perpendicular, we need to understand the conditions for two lines to be perpendicular.
Two lines are perpendicular if the product of their slopes is -1. The slope of a line is given by the coefficient of x divided by the coefficient of y in the equation of the line.
Equation Analysis:
The given equation is: 3ax^2 + 5xy + (a^2 - 2)y^2 = 0
To find the slopes of the lines represented by this equation, we need to convert it into the standard form of a line equation, which is in the form of ax + by + c = 0.
Converting the Equation:
Let's convert the given equation into the standard form by rearranging the terms:
3ax^2 + 5xy + (a^2 - 2)y^2 = 0
3ax^2 + 5xy + a^2y^2 - 2y^2 = 0
3ax^2 + 5xy + a^2y^2 = 2y^2
Now, let's divide the entire equation by y^2 to get rid of the quadratic terms:
(3ax^2 + 5xy + a^2y^2) / y^2 = 2y^2 / y^2
3ax^2 / y^2 + 5xy / y^2 + a^2 = 2
Simplifying further:
3a(x/y)^2 + 5(x/y) + a^2 = 2
Now, let's consider x/y as a new variable, say 'm':
3am^2 + 5m + a^2 - 2 = 0
Conditions for Perpendicular Lines:
For two lines to be perpendicular, the product of their slopes should be -1. Therefore, we need to find the values of 'a' for which the slopes of the lines represented by the given equation satisfy this condition.
Calculating the Slopes:
The slope of the line represented by the given equation can be found by differentiating the equation with respect to x/y and solving for m.
Differentiating the equation 3am^2 + 5m + a^2 - 2 = 0 with respect to m:
6am + 5 = 0
m = -5/6a
Product of Slopes:
Now, let's find the product of the slopes of the two lines represented by the given equation:
m1 * m2 = (-5/6a) * (-5/6a) = 25/36a^2
Condition for Perpendicular Lines:
To find the values of 'a' for which the lines are perpendicular, we need the product of their slopes to be -1.
Therefore, 25/36a^2 = -1
36a^2 = -25
a^2 = -25/36
Solution:
The equation a^2 = -25/36 has no real solutions since the square of a real number cannot be negative.
Therefore, there are no values of 'a' for which
Mark the correct option.- a)Behaviour of moving charge along the circle is equivalent to current carrying circular coil for instantaneous value as well as for average value of magnetic field on its axis
- b) If two identical charge particles are moving symmetrically along a circle then its behaviour with respect to magnetic field on the axis is equivalent to current carrying coil for both average and instantaneous value
- c)For instantaneous value of magnetic field on the axis, the charge moving along a circle is equivalent to current carrying circular coil
- d)Both b and c
Correct answer is option 'B'. Can you explain this answer?
Mark the correct option.
a)
Behaviour of moving charge along the circle is equivalent to current carrying circular coil for instantaneous value as well as for average value of magnetic field on its axis
b)
If two identical charge particles are moving symmetrically along a circle then its behaviour with respect to magnetic field on the axis is equivalent to current carrying coil for both average and instantaneous value
c)
For instantaneous value of magnetic field on the axis, the charge moving along a circle is equivalent to current carrying circular coil
d)
Both b and c

|
Amrita Sarkar answered |
A charge moving along a circle is equivalent to a current carrying coil, but with respect to magnetic field on the axis of circle. It/ is equivalent only for average value of magnetic field and not for instantaneous values. While if two charge particles are moving symmetrically along a circle at diametrically opposite points then the average as well as instantaneous magnetic field on its axis is same as due to a current carrying coil.
The volumes of containers A and B, connected by a tube and a closed valve are V and 4 V, respectively. Both the containers A and B have the same ideal gas at pressures (temperatures) 5.0 ×105 Pa(300 K) and 1.0 ×105Pa (400 K), respectively. The valve is opened to allow the pressure to equalise, but the temperature of each container is kept constant at its initial value. Find the common pressure in the containers.- a)2.5 × 105 Pa
- b)2.0 × 105 Pa
- c)3.0 × 105 Pa
- d)1.5 × 105 Pa
Correct answer is option 'B'. Can you explain this answer?
The volumes of containers A and B, connected by a tube and a closed valve are V and 4 V, respectively. Both the containers A and B have the same ideal gas at pressures (temperatures) 5.0 ×105 Pa(300 K) and 1.0 ×105Pa (400 K), respectively. The valve is opened to allow the pressure to equalise, but the temperature of each container is kept constant at its initial value. Find the common pressure in the containers.
a)
2.5 × 105 Pa
b)
2.0 × 105 Pa
c)
3.0 × 105 Pa
d)
1.5 × 105 Pa

|
Dipanjan Majumdar answered |
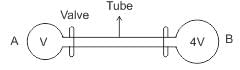
∴ p1 > p2 so, the equalise pressure of the p is reduced from p1
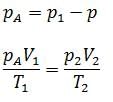
Given, T1 = 300
T2 = 400
V2 = 4V
p1 = 5 x 105
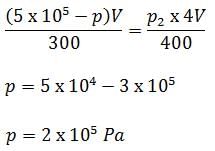
According to the kinetic theory of gases, between two successive collisions, a gas molecule travels- a)In a circular path
- b)In a wavy path
- c)In a straight line path
- d)With an accelerated velocity
Correct answer is option 'C'. Can you explain this answer?
According to the kinetic theory of gases, between two successive collisions, a gas molecule travels
a)
In a circular path
b)
In a wavy path
c)
In a straight line path
d)
With an accelerated velocity
|
|
Varun Kapoor answered |
According to kinetic theory, the gas molecules are in a state of constant rapid motion in all possible directions colliding in a random manner with one another and with the walls of the container and between two successive collisions, molecules travel in a straight line path but show haphazard motion due to collisions.
A circular disc of radius r and thickness r/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted to a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is- a)I/2
- b)2I/11
- c)I/10
- d)I/5
Correct answer is option 'D'. Can you explain this answer?
A circular disc of radius r and thickness r/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted to a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
a)
I/2
b)
2I/11
c)
I/10
d)
I/5

|
Akshita Nair answered |
Volume oc circular disc = surface of area x thickness
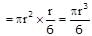
The mass of the circular disc and sphere are the same
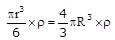
where R is the radius of the sphere,
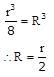
Moment of interia of a circluar disc

Moment of interia of solid sphere
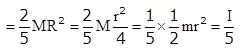
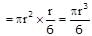
The mass of the circular disc and sphere are the same
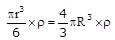
where R is the radius of the sphere,
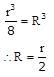
Moment of interia of a circluar disc

Moment of interia of solid sphere
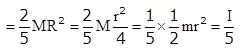
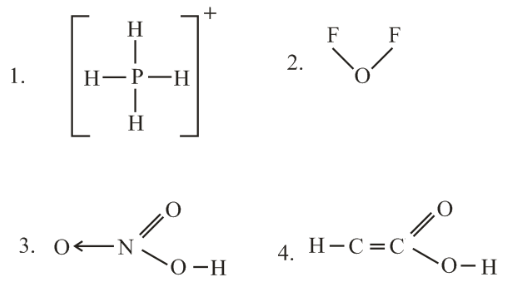
The number of P-O-P bridges in the structures of phosphorus pentoxide and phosphorus trioxide is- a)6, 6
- b)5, 5
- c)5, 6
- d)6, 5
Correct answer is option 'A'. Can you explain this answer?
The number of P-O-P bridges in the structures of phosphorus pentoxide and phosphorus trioxide is
a)
6, 6
b)
5, 5
c)
5, 6
d)
6, 5
|
|
Deepika Sen answered |
Understanding P-O-P Bridges in Phosphorus Compounds
Phosphorus pentoxide (P2O5) and phosphorus trioxide (P2O3) are two important phosphorus oxides that exhibit different bonding structures. The concept of P-O-P (phosphorus-oxygen-phosphorus) bridges is crucial in understanding their molecular frameworks.
Phosphorus Pentoxide (P2O5)
- P2O5 is known to have a dimeric structure consisting of two phosphorus atoms connected by oxygen atoms.
- In its anhydrous form, it primarily exists as a cyclic structure with multiple bridging oxygens.
- The number of P-O-P bridges in P2O5 is 6, as it forms a network with six oxygen atoms linking the phosphorus centers.
Phosphorus Trioxide (P2O3)
- P2O3 features a different structural arrangement compared to P2O5.
- It has a more polymeric structure with fewer bridging oxygens.
- The number of P-O-P bridges in P2O3 is 5, due to the presence of fewer oxygen linkages between the phosphorus atoms.
Summary of Bridges
- Phosphorus Pentoxide (P2O5): 6 P-O-P bridges
- Phosphorus Trioxide (P2O3): 5 P-O-P bridges
Conclusion
The correct answer to the question regarding the number of P-O-P bridges in phosphorus pentoxide and phosphorus trioxide is option 'A': 6 bridges in P2O5 and 5 bridges in P2O3. This understanding of the structural differences underscores the significance of bridging oxygens in determining the properties of these phosphorus oxides.
Phosphorus pentoxide (P2O5) and phosphorus trioxide (P2O3) are two important phosphorus oxides that exhibit different bonding structures. The concept of P-O-P (phosphorus-oxygen-phosphorus) bridges is crucial in understanding their molecular frameworks.
Phosphorus Pentoxide (P2O5)
- P2O5 is known to have a dimeric structure consisting of two phosphorus atoms connected by oxygen atoms.
- In its anhydrous form, it primarily exists as a cyclic structure with multiple bridging oxygens.
- The number of P-O-P bridges in P2O5 is 6, as it forms a network with six oxygen atoms linking the phosphorus centers.
Phosphorus Trioxide (P2O3)
- P2O3 features a different structural arrangement compared to P2O5.
- It has a more polymeric structure with fewer bridging oxygens.
- The number of P-O-P bridges in P2O3 is 5, due to the presence of fewer oxygen linkages between the phosphorus atoms.
Summary of Bridges
- Phosphorus Pentoxide (P2O5): 6 P-O-P bridges
- Phosphorus Trioxide (P2O3): 5 P-O-P bridges
Conclusion
The correct answer to the question regarding the number of P-O-P bridges in phosphorus pentoxide and phosphorus trioxide is option 'A': 6 bridges in P2O5 and 5 bridges in P2O3. This understanding of the structural differences underscores the significance of bridging oxygens in determining the properties of these phosphorus oxides.
A metal conductor of length 1 m rotates vertically about one of its ends at angular velocity 5 radian per second. If the horizontal component of Earth's magnetic field is 0.2 x 10-4 T, then the emf developed between the two ends of the conductor is- a)5 μV
- b)50 μV
- c)5 mV
- d)50 mV
Correct answer is option 'B'. Can you explain this answer?
A metal conductor of length 1 m rotates vertically about one of its ends at angular velocity 5 radian per second. If the horizontal component of Earth's magnetic field is 0.2 x 10-4 T, then the emf developed between the two ends of the conductor is
a)
5 μV
b)
50 μV
c)
5 mV
d)
50 mV
|
|
Chirag Verma answered |
Induced e.m.f. = 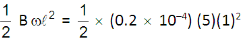
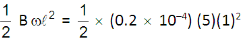
∴ Induced e.m.f = 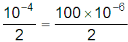
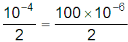
= 50 μV
If statement (P →q) → (q →r) is false, then truth values of statements p,q and r respectively can be- a)FTF
- b)TTT
- c)FFF
- d)FTT
Correct answer is option 'A'. Can you explain this answer?
If statement (P →q) → (q →r) is false, then truth values of statements p,q and r respectively can be
a)
FTF
b)
TTT
c)
FFF
d)
FTT

|
Anand Khanna answered |
If (P →q) →(q →r) is false then (p →q) must be true and (q →r) must be false.
Now,
If P →q is true then P & q both can be true or false :
If q →r is false then q must be true and r must be false
So when both condition i.e. P →q true and q → r false satisfy then q is true, r is false and P can be true or false
Now,
If P →q is true then P & q both can be true or false :
If q →r is false then q must be true and r must be false
So when both condition i.e. P →q true and q → r false satisfy then q is true, r is false and P can be true or false
Which is the most volatile?- a)CH3CH2CH2NH2
- b)(CH3)3N
- c)CH3CH2NHCH3
- d)CH3–CH2–OH
Correct answer is option 'B'. Can you explain this answer?
Which is the most volatile?
a)
CH3CH2CH2NH2
b)
(CH3)3N
c)
CH3CH2NHCH3
d)
CH3–CH2–OH
|
|
Chirag Verma answered |
Volatile nature Volatile nature ∝ 1 / Boiling point
(CH3)3N → No H-bond (less Boiling point)
Hence it is most volatile.
The coefficient of x5 in the expansion of (1 + x)21 + (1 + x)22 +...+(1 + x)30 is- a)51C5
- b)9C5
- c)31C6 - 21C6
- d)30C5 + 20C5
Correct answer is option 'C'. Can you explain this answer?
The coefficient of x5 in the expansion of (1 + x)21 + (1 + x)22 +...+(1 + x)30 is
a)
51C5
b)
9C5
c)
31C6 - 21C6
d)
30C5 + 20C5
|
|
Ananya Das answered |
(1 + x)21 + (1 + x)22 +...+(1 + x)30
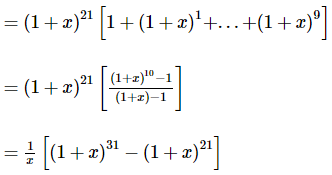
∴ Coefficient of x5 in the given expression
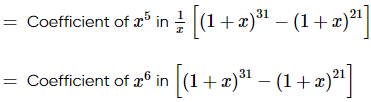
= 31C6 - 21C6
Three point charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown in the figure. If the net electrostatic energy of the configuration is zero, then what is the value of 10×∣Q/q∣? [Take √2 =1.4]
Correct answer is '6'. Can you explain this answer?
Three point charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown in the figure. If the net electrostatic energy of the configuration is zero, then what is the value of 10×∣Q/q∣? [Take √2 =1.4]
|
|
Neha Sharma answered |
Net electrostatic energy of the configuration will be
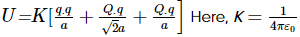
Putting U = 0, we get
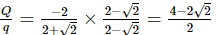
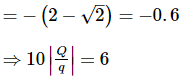
The total number of isotopes of hydrogen and number of radioactive isotopes among them, respectively, are:- a)2 and 0
- b)3 and 2
- c)3 and 1
- d)2 and 1
Correct answer is option 'C'. Can you explain this answer?
The total number of isotopes of hydrogen and number of radioactive isotopes among them, respectively, are:
a)
2 and 0
b)
3 and 2
c)
3 and 1
d)
2 and 1
|
|
Geetika Chakraborty answered |
Isotopes of Hydrogen:
- Hydrogen is the first element in the periodic table and has an atomic number of 1.
- The atomic number determines the number of protons in an atom.
- Hydrogen typically has one proton in its nucleus, but it can have different numbers of neutrons, resulting in isotopes.
- Isotopes of an element have the same number of protons but different numbers of neutrons.
Isotopes of Hydrogen:
- There are three isotopes of hydrogen: protium, deuterium, and tritium.
- Protium is the most common isotope and has one proton and no neutrons.
- Deuterium has one proton and one neutron.
- Tritium has one proton and two neutrons.
Radioactive Isotopes of Hydrogen:
- Radioactive isotopes are isotopes that have an unstable nucleus and undergo radioactive decay.
- This means that they emit radiation in the form of particles or electromagnetic waves.
- Among the isotopes of hydrogen, only tritium is radioactive.
- Tritium undergoes beta decay, where a neutron in the nucleus converts into a proton, emitting a beta particle (electron) and a neutrino.
Correct Answer:
- According to the given options, the correct answer is option 'C' which states that there are 3 isotopes of hydrogen and 1 of them is radioactive.
- This is true as there are indeed three isotopes of hydrogen: protium, deuterium, and tritium.
- Among these, tritium is the only radioactive isotope.
- The other options are incorrect because they either state an incorrect number of isotopes or an incorrect number of radioactive isotopes.
- Hydrogen is the first element in the periodic table and has an atomic number of 1.
- The atomic number determines the number of protons in an atom.
- Hydrogen typically has one proton in its nucleus, but it can have different numbers of neutrons, resulting in isotopes.
- Isotopes of an element have the same number of protons but different numbers of neutrons.
Isotopes of Hydrogen:
- There are three isotopes of hydrogen: protium, deuterium, and tritium.
- Protium is the most common isotope and has one proton and no neutrons.
- Deuterium has one proton and one neutron.
- Tritium has one proton and two neutrons.
Radioactive Isotopes of Hydrogen:
- Radioactive isotopes are isotopes that have an unstable nucleus and undergo radioactive decay.
- This means that they emit radiation in the form of particles or electromagnetic waves.
- Among the isotopes of hydrogen, only tritium is radioactive.
- Tritium undergoes beta decay, where a neutron in the nucleus converts into a proton, emitting a beta particle (electron) and a neutrino.
Correct Answer:
- According to the given options, the correct answer is option 'C' which states that there are 3 isotopes of hydrogen and 1 of them is radioactive.
- This is true as there are indeed three isotopes of hydrogen: protium, deuterium, and tritium.
- Among these, tritium is the only radioactive isotope.
- The other options are incorrect because they either state an incorrect number of isotopes or an incorrect number of radioactive isotopes.
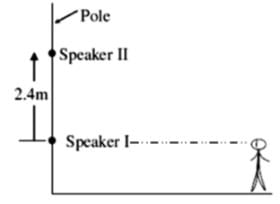
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)- a)a
- b)b
- c)c
- d)d
Correct answer is '7'. Can you explain this answer?
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)
a)
a
b)
b
c)
c
d)
d

|
Lekshmi Bose answered |
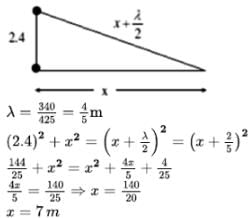
Let x be maximum distance of person from speaker | when he hears no sound (i.e, minimal)
In which one of the following pairs is the radius of the second species greater than that of the first?- a)Na, Mg
- b)Li+, Be2+
- c)Ba2+, Sr2+
- d)O2−, N3−
Correct answer is option 'D'. Can you explain this answer?
In which one of the following pairs is the radius of the second species greater than that of the first?
a)
Na, Mg
b)
Li+, Be2+
c)
Ba2+, Sr2+
d)
O2−, N3−
|
|
Meera Bajaj answered |
Explanation:
Species Comparison:
- The radius of an ion is determined by its electron configuration and the number of protons in its nucleus.
- In general, as you move down a group in the periodic table, the radius of the ions increases due to the addition of new electron shells.
Comparison of Species in each Pair:
a) Na, Mg
- Na is a neutral atom with 11 electrons and Mg is a neutral atom with 12 electrons.
- Mg has a greater number of protons in its nucleus compared to Na, so Mg has a smaller radius than Na.
b) Li+, Be2+
- Li+ has lost one electron compared to the neutral atom Li, so it has a smaller radius.
- Be2+ has lost two electrons compared to the neutral atom Be, so it has an even smaller radius than Li+.
c) Ba2+, Sr2+
- Both Ba and Sr are in the same group in the periodic table, meaning they have the same number of electron shells.
- Since Ba2+ has a greater nuclear charge due to its higher number of protons compared to Sr2+, Ba2+ has a smaller radius.
d) O2-, N3-
- O2- has gained two electrons compared to the neutral atom O, resulting in a larger radius for O2-.
- N3- has gained three electrons compared to the neutral atom N, resulting in a larger radius for N3-.
- Therefore, in this pair, the radius of the second species (N3-) is greater than that of the first species (O2-).
Therefore, the correct answer is option 'D' - O2-, N3-.
Species Comparison:
- The radius of an ion is determined by its electron configuration and the number of protons in its nucleus.
- In general, as you move down a group in the periodic table, the radius of the ions increases due to the addition of new electron shells.
Comparison of Species in each Pair:
a) Na, Mg
- Na is a neutral atom with 11 electrons and Mg is a neutral atom with 12 electrons.
- Mg has a greater number of protons in its nucleus compared to Na, so Mg has a smaller radius than Na.
b) Li+, Be2+
- Li+ has lost one electron compared to the neutral atom Li, so it has a smaller radius.
- Be2+ has lost two electrons compared to the neutral atom Be, so it has an even smaller radius than Li+.
c) Ba2+, Sr2+
- Both Ba and Sr are in the same group in the periodic table, meaning they have the same number of electron shells.
- Since Ba2+ has a greater nuclear charge due to its higher number of protons compared to Sr2+, Ba2+ has a smaller radius.
d) O2-, N3-
- O2- has gained two electrons compared to the neutral atom O, resulting in a larger radius for O2-.
- N3- has gained three electrons compared to the neutral atom N, resulting in a larger radius for N3-.
- Therefore, in this pair, the radius of the second species (N3-) is greater than that of the first species (O2-).
Therefore, the correct answer is option 'D' - O2-, N3-.
In which of the following case, increase in concentration of ion cause increase in Ecell?- a)Pt(H2)|H+(Ag)
- b)Ag,AgCl|Cl−(aq)
- c)Pt|Quinhydrone|H+(aq
- d)Ag|Ag+(aq)
Correct answer is option 'B'. Can you explain this answer?
In which of the following case, increase in concentration of ion cause increase in Ecell?
a)
Pt(H2)|H+(Ag)
b)
Ag,AgCl|Cl−(aq)
c)
Pt|Quinhydrone|H+(aq
d)
Ag|Ag+(aq)
|
|
Meera Bajaj answered |
Explanation:
Increasing the concentration of ions can affect the cell potential in different types of electrochemical cells. Let's analyze the given cases to determine which one shows an increase in Ecell with an increase in ion concentration.
Case B: Ag, AgCl|Cl⁻(aq)
- In this case, the presence of Cl⁻ ions in the solution can react with AgCl to form more Ag+ ions, increasing their concentration.
- The reaction can be represented as: AgCl(s) ⇌ Ag+(aq) + Cl⁻(aq)
- As the concentration of Ag+ ions increases, the equilibrium of the cell reaction shifts to the right, increasing the cell potential (Ecell).
- Therefore, in this case, an increase in ion concentration causes an increase in Ecell.
Other Cases:
- Case A: Pt(H2)|H+(Ag) - This is a hydrogen electrode, and changing the H+ ion concentration does not affect the cell potential significantly.
- Case C: Pt|Quinhydrone|H+(aq) - The cell potential is determined by the redox reaction involving quinhydrone and is not directly influenced by the H+ ion concentration.
- Case D: Ag|Ag+(aq) - The cell potential is primarily determined by the Ag/Ag+ redox couple and is not significantly affected by the Ag+ ion concentration.
Therefore, the correct answer is option B, where an increase in ion concentration leads to an increase in Ecell.
Increasing the concentration of ions can affect the cell potential in different types of electrochemical cells. Let's analyze the given cases to determine which one shows an increase in Ecell with an increase in ion concentration.
Case B: Ag, AgCl|Cl⁻(aq)
- In this case, the presence of Cl⁻ ions in the solution can react with AgCl to form more Ag+ ions, increasing their concentration.
- The reaction can be represented as: AgCl(s) ⇌ Ag+(aq) + Cl⁻(aq)
- As the concentration of Ag+ ions increases, the equilibrium of the cell reaction shifts to the right, increasing the cell potential (Ecell).
- Therefore, in this case, an increase in ion concentration causes an increase in Ecell.
Other Cases:
- Case A: Pt(H2)|H+(Ag) - This is a hydrogen electrode, and changing the H+ ion concentration does not affect the cell potential significantly.
- Case C: Pt|Quinhydrone|H+(aq) - The cell potential is determined by the redox reaction involving quinhydrone and is not directly influenced by the H+ ion concentration.
- Case D: Ag|Ag+(aq) - The cell potential is primarily determined by the Ag/Ag+ redox couple and is not significantly affected by the Ag+ ion concentration.
Therefore, the correct answer is option B, where an increase in ion concentration leads to an increase in Ecell.
The half-life of a radioisotope is six hours. If the initial mass of the isotope is 200 g, then the mass (in g) remaining after 24 hours undecayed will be (Nearest integer)
Correct answer is '13'. Can you explain this answer?
The half-life of a radioisotope is six hours. If the initial mass of the isotope is 200 g, then the mass (in g) remaining after 24 hours undecayed will be (Nearest integer)
|
|
Neha Joshi answered |
Radioactive decay follows first order kinetics.
Number of half-lives (t1/2) = 24/6 = 4
Nt = N0(1/2)4 = N0/16.
1 g of the element will reduce to 1/16g.
Therefore, mass of the radioisotope remaining 1/16 x 200 = 12.5 g = 13 g
Which of the following are substituted purines?A. AdenineB. UracilC. GuanineD. Cytosine- a)Only A and B
- b)Only A and C
- c)Only A and D
- d)Only B and C
Correct answer is option 'B'. Can you explain this answer?
Which of the following are substituted purines?
A. Adenine
B. Uracil
C. Guanine
D. Cytosine
a)
Only A and B
b)
Only A and C
c)
Only A and D
d)
Only B and C
|
|
Sarita Yadav answered |
Adenine and guanine are substituted purines.
Hence, option (b) is correct.
How many of the following are reducing carbohydrates Glucose, Fructose, Sucrose, Lactose, Maltose, Galactose, Cellobiose, Cellulose, Starch, Arabinose, Ribose
Correct answer is '8'. Can you explain this answer?
How many of the following are reducing carbohydrates Glucose, Fructose, Sucrose, Lactose, Maltose, Galactose, Cellobiose, Cellulose, Starch, Arabinose, Ribose
|
|
Sahil Sengupta answered |
Reducing Carbohydrates
• Reducing carbohydrates are those which can act as reducing agents, they have a free aldehyde or ketone group.
• Glucose, fructose, sucrose, lactose, maltose, galactose, cellobiose, and arabinose are reducing carbohydrates.
Non-reducing Carbohydrates
• Non-reducing carbohydrates do not have a free aldehyde or ketone group.
• Cellulose and starch are non-reducing carbohydrates.
• Ribose is a reducing sugar but it is not considered as reducing carbohydrate as it is a monosaccharide.
Answer
Out of the given carbohydrates, eight are reducing carbohydrates, and they are glucose, fructose, sucrose, lactose, maltose, galactose, cellobiose, and arabinose. Glucose, fructose, and galactose are monosaccharides, whereas sucrose, lactose, and maltose are disaccharides. Cellobiose is a reducing disaccharide, whereas arabinose is a reducing pentose sugar. Cellulose and starch are non-reducing carbohydrates as they do not have a free aldehyde or ketone group. Ribose is a reducing sugar, but it is not considered a reducing carbohydrate as it is a monosaccharide.
• Reducing carbohydrates are those which can act as reducing agents, they have a free aldehyde or ketone group.
• Glucose, fructose, sucrose, lactose, maltose, galactose, cellobiose, and arabinose are reducing carbohydrates.
Non-reducing Carbohydrates
• Non-reducing carbohydrates do not have a free aldehyde or ketone group.
• Cellulose and starch are non-reducing carbohydrates.
• Ribose is a reducing sugar but it is not considered as reducing carbohydrate as it is a monosaccharide.
Answer
Out of the given carbohydrates, eight are reducing carbohydrates, and they are glucose, fructose, sucrose, lactose, maltose, galactose, cellobiose, and arabinose. Glucose, fructose, and galactose are monosaccharides, whereas sucrose, lactose, and maltose are disaccharides. Cellobiose is a reducing disaccharide, whereas arabinose is a reducing pentose sugar. Cellulose and starch are non-reducing carbohydrates as they do not have a free aldehyde or ketone group. Ribose is a reducing sugar, but it is not considered a reducing carbohydrate as it is a monosaccharide.
The plane passing through the point (−2, −2, 2) and containing the line joining the points
(1, 1, 1) and (1, −1, 2) makes intercepts on the coordinates axes then sum of the lengths of intercepts is
- a)3
- b)4
- c)6
- d)12
Correct answer is option 'D'. Can you explain this answer?
The plane passing through the point (−2, −2, 2) and containing the line joining the points
(1, 1, 1) and (1, −1, 2) makes intercepts on the coordinates axes then sum of the lengths of intercepts is
(1, 1, 1) and (1, −1, 2) makes intercepts on the coordinates axes then sum of the lengths of intercepts is
a)
3
b)
4
c)
6
d)
12

|
Dipika Choudhury answered |
Equation of any plane passing through (−2, −2, 2) is
a(x + 2) + b(y + 2) + c(z – 2) = 0
Since it contains the line joining the points (1, 1, 1) and (1, −1, 2), it contains these points as well
so that
3a + 3b – c = 0
and 3a + b + 0 = 0
Solving we get
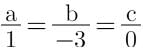
and thus the equation of the plane is
(x + 2) - 3(y + 2) = 0
x+3y-4=0
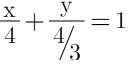
Intercepts on axes = 4, 4/3
The required sum= 4+(4/3)=16/3
a(x + 2) + b(y + 2) + c(z – 2) = 0
Since it contains the line joining the points (1, 1, 1) and (1, −1, 2), it contains these points as well
so that
3a + 3b – c = 0
and 3a + b + 0 = 0
Solving we get
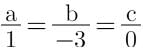
and thus the equation of the plane is
(x + 2) - 3(y + 2) = 0
x+3y-4=0
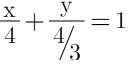
Intercepts on axes = 4, 4/3
The required sum= 4+(4/3)=16/3
An alternating voltage having frequency of 50 cycles/sec and maximum voltage 220 V is supplied to a circuit containing a pure inductance of 0.02 H and a pure resistance of 10 Ω in series. The value of maximum current in circuit is-- a)16.52 A
- b)18.64 A
- c)20.18 A
- d)22. 73 A
Correct answer is option 'B'. Can you explain this answer?
An alternating voltage having frequency of 50 cycles/sec and maximum voltage 220 V is supplied to a circuit containing a pure inductance of 0.02 H and a pure resistance of 10 Ω in series. The value of maximum current in circuit is-
a)
16.52 A
b)
18.64 A
c)
20.18 A
d)
22. 73 A

|
Harshitha Nambiar answered |
Impendance of L.R series circut
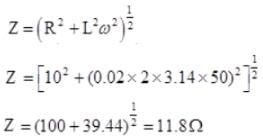
Value of current
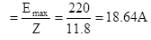
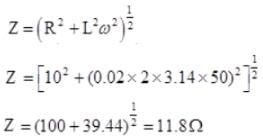
Value of current
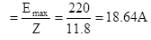
A steel ball of mass 60 g falls from a height 0.8 m on the horizontal surface of a massive slab. The coefficient of restitution between the ball and the slab is e = 0.4; the total momentum imparted to the slab by the ball after numerous bounces is- a)0.56 Ns
- b)0.64 Ns
- c)0.72 Ns
- d)0.78 Ns
Correct answer is option 'A'. Can you explain this answer?
A steel ball of mass 60 g falls from a height 0.8 m on the horizontal surface of a massive slab. The coefficient of restitution between the ball and the slab is e = 0.4; the total momentum imparted to the slab by the ball after numerous bounces is
a)
0.56 Ns
b)
0.64 Ns
c)
0.72 Ns
d)
0.78 Ns

|
Roshni Chavan answered |
Let v be the velocity of the ball on reaching the slab.
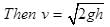
By Newton's law of collision, the velocity v ' after the first im pact is v ' = ev (upward direction).
Similarly, v"=ev' = e2v; v' " = e3v an d so on.
Mom entum im parted to the slab after the first im pact
= mv - (-mv') = m (v + v')
= mv (1 + e )
Similarly, the momentum imparted in the second impact = m(v ' + v ") = m (v ' + e v')
= mv'( 1 + e) = m ( l + e) ev
Momentum im parted to the slab in the third impact
= m (v" + v' " )
= m (v " + ev" )
= m ( 1 + e )v "
= m ( 1 + e ) e2v and so on.
∴ total momentum imparted
= mv ( 1 + e) + mve ( 1 + e)+ mve2( 1 + e) + ...
= mv ( 1 + e) (1 + e + e2 + e3 + ....)
as e < 1
By Newton's law of collision, the velocity v ' after the first im pact is v ' = ev (upward direction).
Similarly, v"=ev' = e2v; v' " = e3v an d so on.
Mom entum im parted to the slab after the first im pact
= mv - (-mv') = m (v + v')
= mv (1 + e )
Similarly, the momentum imparted in the second impact = m(v ' + v ") = m (v ' + e v')
= mv'( 1 + e) = m ( l + e) ev
Momentum im parted to the slab in the third impact
= m (v" + v' " )
= m (v " + ev" )
= m ( 1 + e )v "
= m ( 1 + e ) e2v and so on.
∴ total momentum imparted
= mv ( 1 + e) + mve ( 1 + e)+ mve2( 1 + e) + ...
= mv ( 1 + e) (1 + e + e2 + e3 + ....)
as e < 1
The area bounded by y = 2 – |2 – x|; then k =________
then k =________
Correct answer is '4'. Can you explain this answer?
The area bounded by y = 2 – |2 – x|; then k =________
then k =________
 then k =________
then k =________ |
|
Preeti Iyer answered |
The equation y = 2 - |2 - x| defines two lines:
y = 2 - (2 - x) = x for x >= 2
y = 2 - (-2 + x) = 4 - x for x < 2
The area bounded by these lines is a rectangle with base 2 and height 2. The area of this rectangle is k = 2 * 2 = 4.
Therefore, the value of k is 4.
Which of the following pairs of physical quantities does not have same dimensional formula ?- a)Work and torque
- b)Angular momentum and Planck's constant
- c)Tension and surface tension
- d)Impulse and linear momentum
Correct answer is option 'C'. Can you explain this answer?
Which of the following pairs of physical quantities does not have same dimensional formula ?
a)
Work and torque
b)
Angular momentum and Planck's constant
c)
Tension and surface tension
d)
Impulse and linear momentum
|
|
Divyansh Choudhary answered |
Explanation:
To determine which pair of physical quantities does not have the same dimensional formula, we need to compare the dimensions of each quantity.
Let's analyze each pair:
a) Work and torque:
- Work is defined as the product of force and displacement. Its dimensions can be expressed as [M^1 L^2 T^-2].
- Torque is defined as the product of force and perpendicular distance from the axis of rotation. Its dimensions can be expressed as [M^1 L^2 T^-2].
- The dimensional formulas of work and torque are the same, [M^1 L^2 T^-2]. Therefore, option 'a' is not the correct answer.
b) Angular momentum and Planck's constant:
- Angular momentum is defined as the product of moment of inertia and angular velocity. Its dimensions can be expressed as [M^1 L^2 T^-1].
- Planck's constant is a fundamental constant in quantum mechanics and its dimensions can be expressed as [M^1 L^2 T^-1].
- The dimensional formulas of angular momentum and Planck's constant are the same, [M^1 L^2 T^-1]. Therefore, option 'b' is not the correct answer.
c) Tension and surface tension:
- Tension is the force transmitted through a string, rope, cable, or any other type of flexible connector. Its dimensions can be expressed as [M^1 L^1 T^-2].
- Surface tension is the force per unit length acting perpendicular to an imaginary line drawn on the surface of a liquid. Its dimensions can be expressed as [M^1 T^-2].
- The dimensional formulas of tension and surface tension are different. Therefore, option 'c' is the correct answer.
d) Impulse and linear momentum:
- Impulse is defined as the change in momentum of an object. Its dimensions can be expressed as [M^1 L^1 T^-1].
- Linear momentum is defined as the product of mass and velocity. Its dimensions can be expressed as [M^1 L^1 T^-1].
- The dimensional formulas of impulse and linear momentum are the same, [M^1 L^1 T^-1]. Therefore, option 'd' is not the correct answer.
Therefore, the correct answer is option 'C' - Tension and surface tension.
To determine which pair of physical quantities does not have the same dimensional formula, we need to compare the dimensions of each quantity.
Let's analyze each pair:
a) Work and torque:
- Work is defined as the product of force and displacement. Its dimensions can be expressed as [M^1 L^2 T^-2].
- Torque is defined as the product of force and perpendicular distance from the axis of rotation. Its dimensions can be expressed as [M^1 L^2 T^-2].
- The dimensional formulas of work and torque are the same, [M^1 L^2 T^-2]. Therefore, option 'a' is not the correct answer.
b) Angular momentum and Planck's constant:
- Angular momentum is defined as the product of moment of inertia and angular velocity. Its dimensions can be expressed as [M^1 L^2 T^-1].
- Planck's constant is a fundamental constant in quantum mechanics and its dimensions can be expressed as [M^1 L^2 T^-1].
- The dimensional formulas of angular momentum and Planck's constant are the same, [M^1 L^2 T^-1]. Therefore, option 'b' is not the correct answer.
c) Tension and surface tension:
- Tension is the force transmitted through a string, rope, cable, or any other type of flexible connector. Its dimensions can be expressed as [M^1 L^1 T^-2].
- Surface tension is the force per unit length acting perpendicular to an imaginary line drawn on the surface of a liquid. Its dimensions can be expressed as [M^1 T^-2].
- The dimensional formulas of tension and surface tension are different. Therefore, option 'c' is the correct answer.
d) Impulse and linear momentum:
- Impulse is defined as the change in momentum of an object. Its dimensions can be expressed as [M^1 L^1 T^-1].
- Linear momentum is defined as the product of mass and velocity. Its dimensions can be expressed as [M^1 L^1 T^-1].
- The dimensional formulas of impulse and linear momentum are the same, [M^1 L^1 T^-1]. Therefore, option 'd' is not the correct answer.
Therefore, the correct answer is option 'C' - Tension and surface tension.
The number of positive integral values of x satisfying the equation [x/13] = [x/17] is n, where [⋅] denotes the greatest integer function, then n/3 is equal to
Correct answer is '9'. Can you explain this answer?
The number of positive integral values of x satisfying the equation [x/13] = [x/17] is n, where [⋅] denotes the greatest integer function, then n/3 is equal to
|
|
Rajeev Choudhary answered |
[x] represents the greatest integer less than or equal to x. We can rewrite the equation as follows:
[x/13] = [x/17]
This equation can be rewritten as:
13([x/13]) = 17([x/17])
13([x/13]) = 17([x/13] + [x/17])
13([x/13]) = 17([x/13] + 1)
13([x/13]) = 17([x/13]) + 17
-4([x/13]) = 17
([x/13]) = -17/4
Since the greatest integer less than or equal to -17/4 is -5, there are no positive integral values of x satisfying the equation. Therefore, n = 0.
[x/13] = [x/17]
This equation can be rewritten as:
13([x/13]) = 17([x/17])
13([x/13]) = 17([x/13] + [x/17])
13([x/13]) = 17([x/13] + 1)
13([x/13]) = 17([x/13]) + 17
-4([x/13]) = 17
([x/13]) = -17/4
Since the greatest integer less than or equal to -17/4 is -5, there are no positive integral values of x satisfying the equation. Therefore, n = 0.
Two vertical poles AL and BM of heights 20 m and 80 m respectively stand apart on a horizontal plane. If A and B be the feet of the poles and AM and BL intersect at P, then the height of P is equal to- a)50 m
- b)18 m
- c)16 m
- d)15 m
Correct answer is option 'C'. Can you explain this answer?
Two vertical poles AL and BM of heights 20 m and 80 m respectively stand apart on a horizontal plane. If A and B be the feet of the poles and AM and BL intersect at P, then the height of P is equal to
a)
50 m
b)
18 m
c)
16 m
d)
15 m
|
|
Sanaya Patel answered |
Given information:
- Heights of poles AL and BM are 20 m and 80 m respectively.
- P is the point where AM and BL intersect.
- We need to find the height of point P.
Solution:
Step 1: Find the distance AP and BP
- Using similar triangles, we can find the distance AP and BP.
- Let x be the distance AP and y be the distance BP.
- By similar triangles, we have x/20 = (x+y)/80.
- Solving this equation, we get x = 16 m and y = 64 m.
Step 2: Find the height of point P
- The height of point P is the sum of the heights of poles AL and BM at point P.
- Height of P = 20 + (80 - 64) = 20 + 16 = 36 m.
Therefore, the height of point P is 36 m, which is option 'C'.
A beam of light traveling in water strikes a glass plate which is also immersed in water. When the angle of incidence is 50 ° the reflected beam is found to be plane polarised. The refractive index of water is 4/3. The refractive index of the glass plate is (Given tan 50 ° = 1.198)- a)1.54
- b)1.57
- c)1.60
- d)1.63
Correct answer is option 'C'. Can you explain this answer?
A beam of light traveling in water strikes a glass plate which is also immersed in water. When the angle of incidence is 50 ° the reflected beam is found to be plane polarised. The refractive index of water is 4/3. The refractive index of the glass plate is (Given tan 50 ° = 1.198)
a)
1.54
b)
1.57
c)
1.60
d)
1.63

|
Amrita Sarkar answered |
by brewster's law,
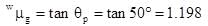
This is the refractive index of glass w.r.to water.
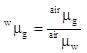
∴ refractive index of glass
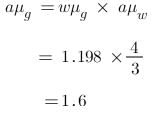
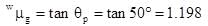
This is the refractive index of glass w.r.to water.
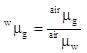
∴ refractive index of glass
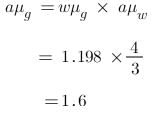
The differential equation whose solution is Ax2 + By2 = 1, where A and B are arbitrary constants, is of- a)second order and second degree
- b)first order and second degree
- c)first order and first degree
- d)second order and first degree
Correct answer is option 'D'. Can you explain this answer?
The differential equation whose solution is Ax2 + By2 = 1, where A and B are arbitrary constants, is of
a)
second order and second degree
b)
first order and second degree
c)
first order and first degree
d)
second order and first degree
|
|
Maya Sharma answered |
The Differential Equation Analysis
To determine the type of differential equation, we start with the given equation:
Ax² + By² = 1
where A and B are arbitrary constants.
Step 1: Understanding the Equation
- The equation represents an ellipse in the Cartesian coordinate system.
- Here, x and y are the variables, while A and B are constants defining the shape and orientation of the ellipse.
Step 2: Differentiating the Equation
To find the associated differential equation, we need to eliminate the constants A and B. We can do this by differentiating the given equation with respect to x:
- Differentiate implicitly:
d/dx (Ax² + By²) = d/dx(1)
This results in:
- 2Ax + 2Byy' = 0 (where y' = dy/dx)
Step 3: Rearranging the Equation
- Rearranging gives us:
2Byy' = -2Ax
- Thus, we can express y' in terms of x and y:
y' = -Ax/(By)
Step 4: Classifying the Differential Equation
Now, we analyze the resulting equation:
- Order: The highest derivative present is y', which is the first derivative. Therefore, it is a first-order differential equation.
- Degree: The equation is linear in terms of y', meaning there are no powers greater than one. Thus, it is of the first degree.
Final Classification
Based on the analysis, the correct classification of the differential equation is:
- First Order and First Degree
Thus, the answer is option 'D'.
To determine the type of differential equation, we start with the given equation:
Ax² + By² = 1
where A and B are arbitrary constants.
Step 1: Understanding the Equation
- The equation represents an ellipse in the Cartesian coordinate system.
- Here, x and y are the variables, while A and B are constants defining the shape and orientation of the ellipse.
Step 2: Differentiating the Equation
To find the associated differential equation, we need to eliminate the constants A and B. We can do this by differentiating the given equation with respect to x:
- Differentiate implicitly:
d/dx (Ax² + By²) = d/dx(1)
This results in:
- 2Ax + 2Byy' = 0 (where y' = dy/dx)
Step 3: Rearranging the Equation
- Rearranging gives us:
2Byy' = -2Ax
- Thus, we can express y' in terms of x and y:
y' = -Ax/(By)
Step 4: Classifying the Differential Equation
Now, we analyze the resulting equation:
- Order: The highest derivative present is y', which is the first derivative. Therefore, it is a first-order differential equation.
- Degree: The equation is linear in terms of y', meaning there are no powers greater than one. Thus, it is of the first degree.
Final Classification
Based on the analysis, the correct classification of the differential equation is:
- First Order and First Degree
Thus, the answer is option 'D'.
Find the angular speed of the meter stick, when a person throws it such that the centre of the stick is moving with a speed of 10 m s-1 vertically upwards & left end of stick with a speed of 20 m s-1 vertically upwards.- a)20 rad s-1
- b)10 rad s-1
- c)30 rad s-1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the angular speed of the meter stick, when a person throws it such that the centre of the stick is moving with a speed of 10 m s-1 vertically upwards & left end of stick with a speed of 20 m s-1 vertically upwards.
a)
20 rad s-1
b)
10 rad s-1
c)
30 rad s-1
d)
None of these
|
|
Gaurav Kumar answered |
Given velocity of centre C of the rod, vC = 10 m s−1
and velocity of end A of the rod vA = 20 m s−1
Let ω be the angular velocity of the rod.
Since vA > vC, thus the stick will rotate in clockwise direction.
Now using the relation, vA − vC = ωr, we get,
⇒ 20 − 10 = ω(l/2)
⇒10 = ω/2 rad s−1
⇒ ω = 20 rad s-1
Hence, the angular speed of the stick is 20 rad s−1.
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ..., 49. Then, the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals- a)1/7
- b)5/14
- c)1/50
- d)1/14
Correct answer is option 'D'. Can you explain this answer?
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ..., 49. Then, the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
a)
1/7
b)
5/14
c)
1/50
d)
1/14
|
|
Neha Joshi answered |
Any number in the set, S = {00, 01, 02, ...., 49} is of the form ab, where a ∈ {0, 1, 2, 3, 4} and b ∈ {0, 1, 2, ..., 9}
For the product of digits to be zero, the numbers must be of the form either a0, which are 5 in number because a ∈ {0, 1, 2, 3, 4} or of the form 0b, which are 10 in number because b ∈ {0, 1, 2, ..., 9}.
The only number common to both = 00
Thus, the number of numbers in S, the product of which is zero = 10 + 5 - 1 = 14
Of these, the number whose sum of digits is 8 is just one i.e. 08.
The required probability = 1/14
Chapter doubts & questions for JEE Main Practice Tests - Mock Tests for JEE Main and Advanced 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of JEE Main Practice Tests - Mock Tests for JEE Main and Advanced 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily