All Exams >
Commerce >
Applied Mathematics for Class 12 >
All Questions
All questions of Higher Order Derivatives for Commerce Exam
If xy = 2, then dy/dx is- a)-x2/2
- b)y2
- c)-2/x2
- d)-y/x
Correct answer is option 'D'. Can you explain this answer?
If xy = 2, then dy/dx is
a)
-x2/2
b)
y2
c)
-2/x2
d)
-y/x
|
Hansa Sharma answered |
xy = 2
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
Differentiate sin2(θ2 + 1) with respect to θ2- a)sin(2θ2 + 1)
- b)cos(2θ2 + 2)
- c)sin(2θ2 + 2)
- d)cos(2θ2 + 1)
Correct answer is option 'C'. Can you explain this answer?
Differentiate sin2(θ2 + 1) with respect to θ2
a)
sin(2θ2 + 1)
b)
cos(2θ2 + 2)
c)
sin(2θ2 + 2)
d)
cos(2θ2 + 1)
|
Gunjan Lakhani answered |
y = sin2(θ2+1)
v = θ2
dy/d(v) = dydθ/dvdθ
dy/dthη = sin2(V+1)
= 2sin(V+1)⋅cos(V+1)dv/dθ
= 2sin(θ2+1)cos(θ2+1)
= sin2(θ2+1).
v = θ2
dy/d(v) = dydθ/dvdθ
dy/dthη = sin2(V+1)
= 2sin(V+1)⋅cos(V+1)dv/dθ
= 2sin(θ2+1)cos(θ2+1)
= sin2(θ2+1).
If 3 sin(xy) + 4 cos (xy) = 5, then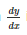 
= .....- a)
- b)
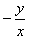
- c)
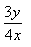
- d)
Correct answer is option 'B'. Can you explain this answer?
If 3 sin(xy) + 4 cos (xy) = 5, then = .....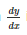
= .....a)
b)
c)
d)
|
Krishna Iyer answered |
3sinxy + 4cosxy = 5
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
- a)
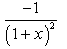
- b)
- c)
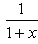
- d)
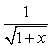
Correct answer is option 'A'. Can you explain this answer?
a)
b)
c)
d)
|
Sushil Kumar answered |
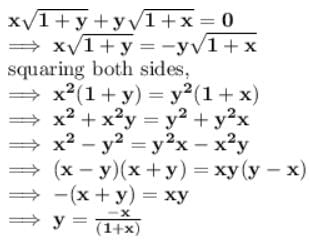
now differentiate y with respect to x,
dy/dx = -{[x d/dx(1+x) - (1+x)dx/dx]}/(1+x2)
= -1/(1+x)2
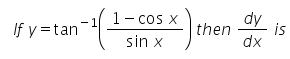
Correct answer is option 'A'. Can you explain this answer?
|
Aryan Khanna answered |
y = tan-1(1-cosx)/sinx
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
- a)
- b)
- c)
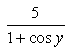
- d)
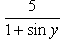
Correct answer is option 'C'. Can you explain this answer?
a)
b)
c)
d)
|
Poonam Reddy answered |
y + sin y = 5x
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
- a)
- b)
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
a)
b)
c)
d)
|
Suhani Dangarh answered |
Put x=tan thita. then you will get. 2 tan inverse x then differentiate
- a)
- b)
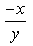
- c)
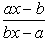
- d)
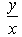
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
Rocky Gupta answered |
X^a y^b = (x + y)^(a + b)
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer
- a)
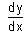
- b)
- c)
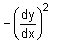
- d)
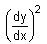
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
Knowledge Hub answered |
ey =1/ (x+5)
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
- a) Continuous at x = 0
- b) Continuous in (-1, 0)
- c) Differentiable at x = 1
- d) Differentiable in (-1, 1)
Correct answer is option 'A'. Can you explain this answer?
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
a)
Continuous at x = 0b)
Continuous in (-1, 0)c)
Differentiable at x = 1d)
Differentiable in (-1, 1)|
|
Asha Choudhury answered |
Solution:
To determine the continuity and differentiability of f(x), we need to evaluate left-hand limit, right-hand limit and the derivative of f(x) at every point in the domain of f(x).
Left-hand limit of f(x):
As x approaches 0 from the left, [x] approaches -1 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between -x and x. Thus, the left-hand limit of f(x) as x approaches 0 is:
lim x→0- f(x) = lim x→0- [x sin(px)] = lim x→0- (-x) = 0.
Right-hand limit of f(x):
As x approaches 0 from the right, [x] approaches 0 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between 0 and x. Thus, the right-hand limit of f(x) as x approaches 0 is:
lim x→0+ f(x) = lim x→0+ [x sin(px)] = lim x→0+ (0) = 0.
Since the left-hand limit and right-hand limit are equal, f(x) is continuous at x=0.
Derivative of f(x):
For x≠0, f(x) is piecewise linear with slope sin(px) and jump discontinuity at every integer multiple of 1/p. Therefore, f(x) is not differentiable at these points.
Since f(x) is continuous at x=0 and not differentiable at any other point, the correct answer is option 'A'.
To determine the continuity and differentiability of f(x), we need to evaluate left-hand limit, right-hand limit and the derivative of f(x) at every point in the domain of f(x).
Left-hand limit of f(x):
As x approaches 0 from the left, [x] approaches -1 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between -x and x. Thus, the left-hand limit of f(x) as x approaches 0 is:
lim x→0- f(x) = lim x→0- [x sin(px)] = lim x→0- (-x) = 0.
Right-hand limit of f(x):
As x approaches 0 from the right, [x] approaches 0 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between 0 and x. Thus, the right-hand limit of f(x) as x approaches 0 is:
lim x→0+ f(x) = lim x→0+ [x sin(px)] = lim x→0+ (0) = 0.
Since the left-hand limit and right-hand limit are equal, f(x) is continuous at x=0.
Derivative of f(x):
For x≠0, f(x) is piecewise linear with slope sin(px) and jump discontinuity at every integer multiple of 1/p. Therefore, f(x) is not differentiable at these points.
Since f(x) is continuous at x=0 and not differentiable at any other point, the correct answer is option 'A'.
- a)2t
- b)1/2a
- c)-t/2a
- d)t/4a
Correct answer is option 'B'. Can you explain this answer?
a)
2t
b)
1/2a
c)
-t/2a
d)
t/4a
|
Om Desai answered |
y = at4, x = 2at2
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
Differentiate sin x3 with respect to x3- a)sin x3
- b)cos x3
- c)– cos x3
- d)– sin x3
Correct answer is option 'B'. Can you explain this answer?
Differentiate sin x3 with respect to x3
a)
sin x3
b)
cos x3
c)
– cos x3
d)
– sin x3
|
Nabanita Bajaj answered |
Differentiating sin(x^3) with respect to x^3:
To differentiate sin(x^3) with respect to x^3, we can use the chain rule of differentiation. The chain rule states that if we have a composite function, the derivative is equal to the derivative of the outer function multiplied by the derivative of the inner function.
Mathematically, let's represent sin(x^3) as f(g(x)), where g(x) = x^3 and f(x) = sin(x).
- The derivative of g(x) = x^3 with respect to x^3 is simply 1, as x^3 is the inner function.
- The derivative of f(x) = sin(x) with respect to x is cos(x), as it is a standard result from trigonometry.
Now we can apply the chain rule:
df(g(x))/dx = df(g(x))/dg(x) * dg(x)/dx
Substituting the values:
df(g(x))/dg(x) = df(g(x))/dx^3 = cos(x^3)
dg(x)/dx = dg(x)/dx^3 = 1
Therefore,
df(g(x))/dx = cos(x^3) * 1 = cos(x^3)
So, the correct answer is option 'B', which is cos(x^3).
To differentiate sin(x^3) with respect to x^3, we can use the chain rule of differentiation. The chain rule states that if we have a composite function, the derivative is equal to the derivative of the outer function multiplied by the derivative of the inner function.
Mathematically, let's represent sin(x^3) as f(g(x)), where g(x) = x^3 and f(x) = sin(x).
- The derivative of g(x) = x^3 with respect to x^3 is simply 1, as x^3 is the inner function.
- The derivative of f(x) = sin(x) with respect to x is cos(x), as it is a standard result from trigonometry.
Now we can apply the chain rule:
df(g(x))/dx = df(g(x))/dg(x) * dg(x)/dx
Substituting the values:
df(g(x))/dg(x) = df(g(x))/dx^3 = cos(x^3)
dg(x)/dx = dg(x)/dx^3 = 1
Therefore,
df(g(x))/dx = cos(x^3) * 1 = cos(x^3)
So, the correct answer is option 'B', which is cos(x^3).
If f(x) = x + cot x,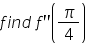 
- a)-4
- b)2
- c)4
- d)-2
Correct answer is option 'C'. Can you explain this answer?
If f(x) = x + cot x,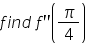
a)
-4
b)
2
c)
4
d)
-2
|
|
Aryan Khanna answered |
f(x) = x + cot x
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
Find the second derivative of excosx- a)-2exsinx
- b)-exsinx
- c)ex(sinx + cosx)
- d)-2excosx
Correct answer is option 'A'. Can you explain this answer?
Find the second derivative of excosx
a)
-2exsinx
b)
-exsinx
c)
ex(sinx + cosx)
d)
-2excosx
|
Rounak Nair answered |
**Solution:**
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
- a)
- b)
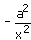
- c)
- d)none
Correct answer is option 'B'. Can you explain this answer?
a)
b)
c)
d)
none
|
|
Nikita Singh answered |
Difference equation are the equations used in discrete time systems and difference equations are similar to the differential equation in continuous systems.
Derivative of cos 
with respect to x is- a)
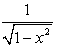
- b)
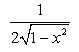
- c)
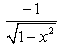
- d)
Correct answer is option 'D'. Can you explain this answer?
Derivative of cos with respect to x is
with respect to x isa)
b)
c)
d)
|
Ashim Pattanaik answered |
Let x= cos2A then root of 1+cos2A /2 = cosA .So cos^-1( cosA) =A=(cos^-1 x )/2.Then by using derivative we can find out -1/2root 1-x^2
Find the differential coefficient y = (sec 5x)5x - a)log ( sec 5x) + 5x log (tan 5x)
- b)5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
- c)(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
- d)log (sec 5x) + 5x tan 5x
Correct answer is option 'B'. Can you explain this answer?
Find the differential coefficient y = (sec 5x)5x
a)
log ( sec 5x) + 5x log (tan 5x)
b)
5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
c)
(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
d)
log (sec 5x) + 5x tan 5x
|
Angelica Das answered |
Take log of both sides then differentiate with respect to x. then replace the value of y in the equation
Differentiate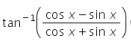 
with respect to x. - a)-1
- b)
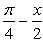
- c)π/4 − x
- d)1
Correct answer is option 'A'. Can you explain this answer?
Differentiate 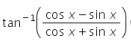with respect to x.
with respect to x. a)
-1
b)
c)
π/4 − x
d)
1
|
|
Krishna Iyer answered |
(cosx − sinx)/(cosx + sinx) = (1 − tanx)/(1 + tanx)
tan(A − B) = (tanA − tanB)/(1 + tanAtanB)
= tan(π/4−x)
putting this value in question.
tan−1 tan(π/4−x)
π/4 − x.
tan(A − B) = (tanA − tanB)/(1 + tanAtanB)
= tan(π/4−x)
putting this value in question.
tan−1 tan(π/4−x)
π/4 − x.
so d(π/4 − x)/dx = -1
- a)π/2
- b)∞
- c)1
Correct answer is option 'C'. Can you explain this answer?
a)
π/2
b)
∞
c)
1
|
Uday Chakraborty answered |
x = a(t+sin t)
⟹dx/dt = a(1+cos t)
And y = a(1−cos t)
⟹dy/dt = a[0−(−sin t)]
=a sin t
Therefore, dy/dx = a sin t/(a(1+cos t))
= 2sin t/2 cos t/2)/(2cos^2 t/2)
=tan(t/2)
At pi/2 = tan(pi/2) = 1
⟹dx/dt = a(1+cos t)
And y = a(1−cos t)
⟹dy/dt = a[0−(−sin t)]
=a sin t
Therefore, dy/dx = a sin t/(a(1+cos t))
= 2sin t/2 cos t/2)/(2cos^2 t/2)
=tan(t/2)
At pi/2 = tan(pi/2) = 1
The general solution of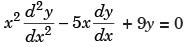
is- a)(c1 + c2x)e3x
- b)(c1 + c2 In x)x3
- c)(c1 + c2 x)x3
- d)(c1 + c2 In x)ex3
Correct answer is option 'B'. Can you explain this answer?
The general solution of
a)
(c1 + c2x)e3x
b)
(c1 + c2 In x)x3
c)
(c1 + c2 x)x3
d)
(c1 + c2 In x)ex3
|
Varun Kapoor answered |
The operator form of given equation is (x2D2 – 5xD + 9)y = 0 ...(*)
Let x = et ⇒ t = log x D′ ≡ d / dt
D ≡ d / dt
We have x2D2 = D′(D′ – 1)
xD = D′
[D′(D′ – 1) – 5D′ + 9]y = 0
The A.E. is m2 – 6m + 9 = 0
(m – 3)2 = 0, m = 3, 3
The C.F. is y = (c
The solution of (*) is
y = (c1 + c2 log x) x3.
Let x = et ⇒ t = log x D′ ≡ d / dt
D ≡ d / dt
We have x2D2 = D′(D′ – 1)
xD = D′
[D′(D′ – 1) – 5D′ + 9]y = 0
The A.E. is m2 – 6m + 9 = 0
(m – 3)2 = 0, m = 3, 3
The C.F. is y = (c
1
+ c2t)e3t The solution of (*) is
y = (c1 + c2 log x) x3.
Differentiate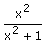 
with respect to x2- a)
- b)
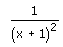
- c)
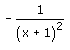
- d)
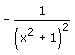
Correct answer is option 'A'. Can you explain this answer?
Differentiate 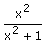with respect to x2
with respect to x2a)
b)
c)
d)
|
Saikat Dasgupta answered |
If you are studying maths, then you should learn the Quotient Rule for Differentiation, and practice how to use it:
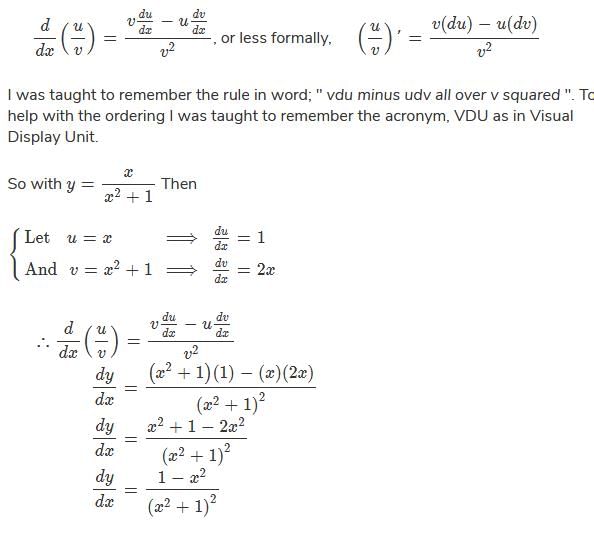
Find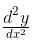 
; x = 20 (cos t + t sin t) and y = 20 ( sin t - t cos t)
- a)Sec2t / 20t
- b)Sec3t / 20t3
- c)Sec3t / 20t
- d)Sec3t / 30t
Correct answer is option 'C'. Can you explain this answer?
Find 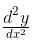; x = 20 (cos t + t sin t) and y = 20 ( sin t - t cos t)
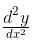; x = 20 (cos t + t sin t) and y = 20 ( sin t - t cos t)a)
Sec2t / 20t
b)
Sec3t / 20t3
c)
Sec3t / 20t
d)
Sec3t / 30t
|
|
Hansa Sharma answered |
x = 20(cost + tsint)
differentiate x with respect to t,
dx/dt = 20{d(cost)/dt + d(tsint)/dt]
= 20[-sint + {t. d(sint)/dt + sint.dt/dt}]
= 20[ -sint + tcost + sint]
= -20t.cost
hence, dx/dt = -20t.cost -----(1)
y = 20(sint - tcost)
differentiate y with respect to t,
dy/dt = 20[d(sint)/dt - d(tcost)/dt ]
= 20[cost - {t.d(cost)/dt + cost.dt/dt}]
= 20[cost +tsint -cost]
= 20t.sint
hence, dy/dt = 20t.sint -------(2)
dividing equations (2) by (1),
dy/dx = 20t.sint/20t.cost
dy/dx = tant
now again differentiate with respect to x
d²y/dx² = sec²t. dt/dx ------(3)
now from equation (1),
dx/dt = 20t.cost
so, dt/dx =1/at.cost put it in equation (3),
e.g., d²y/dx² = sec²t. 1/20t.cost
d²y/dx² = sec³t/20t
differentiate x with respect to t,
dx/dt = 20{d(cost)/dt + d(tsint)/dt]
= 20[-sint + {t. d(sint)/dt + sint.dt/dt}]
= 20[ -sint + tcost + sint]
= -20t.cost
hence, dx/dt = -20t.cost -----(1)
y = 20(sint - tcost)
differentiate y with respect to t,
dy/dt = 20[d(sint)/dt - d(tcost)/dt ]
= 20[cost - {t.d(cost)/dt + cost.dt/dt}]
= 20[cost +tsint -cost]
= 20t.sint
hence, dy/dt = 20t.sint -------(2)
dividing equations (2) by (1),
dy/dx = 20t.sint/20t.cost
dy/dx = tant
now again differentiate with respect to x
d²y/dx² = sec²t. dt/dx ------(3)
now from equation (1),
dx/dt = 20t.cost
so, dt/dx =1/at.cost put it in equation (3),
e.g., d²y/dx² = sec²t. 1/20t.cost
d²y/dx² = sec³t/20t
Chapter doubts & questions for Higher Order Derivatives - Applied Mathematics for Class 12 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Higher Order Derivatives - Applied Mathematics for Class 12 in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Applied Mathematics for Class 12
64 videos|110 docs|63 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup