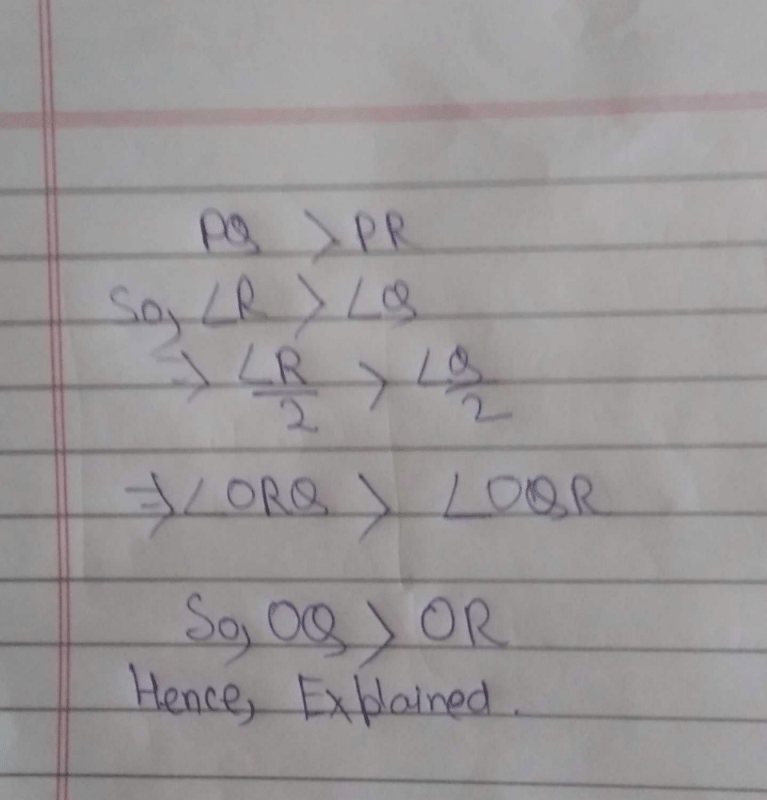All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Triangles for Class 9 Exam
If AB = QR, BC=RP and CA = QP, then which of the following holds?
- a)△BCA ≅ △PQR
- b)△ABC ≅ △PQR
- c)△CBA ≅ △PQR
- d)△CAB ≅ △PQR
Correct answer is option 'D'. Can you explain this answer?
If AB = QR, BC=RP and CA = QP, then which of the following holds?
a)
△BCA ≅ △PQR
b)
△ABC ≅ △PQR
c)
△CBA ≅ △PQR
d)
△CAB ≅ △PQR
|
|
Vani Patel answered |
It is not possible to determine which of the options holds based on the given information.
In the adjoining figure, BC = AC. If ∠ACD = 115∘, the ∠A is

- a)70∘
- b)57.5∘
- c)65∘
- d)50∘
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, BC = AC. If ∠ACD = 115∘, the ∠A is
a)
70∘
b)
57.5∘
c)
65∘
d)
50∘
|
|
C K Academy answered |
In △ABC,
∠ACD+∠ACB = 180∘ (Linear pair)
115∘+∠ACB =180∘
∠ACB = 180∘−115∘=65∘
x + x + 65∘ = 180∘
2x = 180∘- 65∘
2x = 115∘
x = 57.5∘
∠ACD+∠ACB = 180∘ (Linear pair)
115∘+∠ACB =180∘
∠ACB = 180∘−115∘=65∘
x + x + 65∘ = 180∘
2x = 180∘- 65∘
2x = 115∘
x = 57.5∘
In ΔABC and ΔPBC, AB = BP and AC = PC. Can you say whether the triangles are congruent to each other or not:- a)Yes, by ASA Congruence theorem they are congruent
- b)Yes, by SAS Congruence theorem they are congruent
- c)No, they are not congruent
- d)Yes, by SSS Congruence theorem they are congruent
Correct answer is option 'D'. Can you explain this answer?
In ΔABC and ΔPBC, AB = BP and AC = PC. Can you say whether the triangles are congruent to each other or not:
a)
Yes, by ASA Congruence theorem they are congruent
b)
Yes, by SAS Congruence theorem they are congruent
c)
No, they are not congruent
d)
Yes, by SSS Congruence theorem they are congruent
|
|
Sachi Shah answered |
Given that AB = BP and AC = PC, we need to determine whether triangles ABC and PBC are congruent or not. Let's analyze the options one by one.
a) Yes, by ASA Congruence theorem they are congruent.
According to the ASA (Angle-Side-Angle) Congruence theorem, two triangles are congruent if they have two corresponding angles and the included side equal. However, in this case, we only know that the corresponding sides are equal, but we don't have any information about the angles. Therefore, we cannot conclude that the triangles are congruent using the ASA Congruence theorem.
b) Yes, by SAS Congruence theorem they are congruent.
According to the SAS (Side-Angle-Side) Congruence theorem, two triangles are congruent if they have two corresponding sides and the included angle equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides, but we don't have any information about the included angle. Therefore, we cannot conclude that the triangles are congruent using the SAS Congruence theorem.
c) No, they are not congruent.
This option suggests that the triangles are not congruent without providing any reasoning. We cannot simply say that the triangles are not congruent without any valid justification.
d) Yes, by SSS Congruence theorem they are congruent.
According to the SSS (Side-Side-Side) Congruence theorem, two triangles are congruent if they have three corresponding sides equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides. Additionally, we know that BC = BC since it is a common side. Therefore, all three corresponding sides of the triangles are equal, satisfying the condition for congruence by the SSS Congruence theorem. Hence, we can conclude that the triangles ABC and PBC are congruent.
In conclusion, the correct answer is option 'd'. The triangles ABC and PBC are congruent by the SSS Congruence theorem as all three corresponding sides are equal.
a) Yes, by ASA Congruence theorem they are congruent.
According to the ASA (Angle-Side-Angle) Congruence theorem, two triangles are congruent if they have two corresponding angles and the included side equal. However, in this case, we only know that the corresponding sides are equal, but we don't have any information about the angles. Therefore, we cannot conclude that the triangles are congruent using the ASA Congruence theorem.
b) Yes, by SAS Congruence theorem they are congruent.
According to the SAS (Side-Angle-Side) Congruence theorem, two triangles are congruent if they have two corresponding sides and the included angle equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides, but we don't have any information about the included angle. Therefore, we cannot conclude that the triangles are congruent using the SAS Congruence theorem.
c) No, they are not congruent.
This option suggests that the triangles are not congruent without providing any reasoning. We cannot simply say that the triangles are not congruent without any valid justification.
d) Yes, by SSS Congruence theorem they are congruent.
According to the SSS (Side-Side-Side) Congruence theorem, two triangles are congruent if they have three corresponding sides equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides. Additionally, we know that BC = BC since it is a common side. Therefore, all three corresponding sides of the triangles are equal, satisfying the condition for congruence by the SSS Congruence theorem. Hence, we can conclude that the triangles ABC and PBC are congruent.
In conclusion, the correct answer is option 'd'. The triangles ABC and PBC are congruent by the SSS Congruence theorem as all three corresponding sides are equal.
In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :- a)6 cm
- b)8 cm
- c)7 cm
- d)10 cm
Correct answer is option 'B'. Can you explain this answer?
In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :
a)
6 cm
b)
8 cm
c)
7 cm
d)
10 cm
|
|
Prasenjit Menon answered |
Given:
- QR < 2pq="" -="" />
- PR = PQ + 10
- PQ + QR + PR = 40
To find:
The length of the smallest side of the triangle PQR.
Solution:
1. Simplify the first equation:
QR < 2pq="" -="" 2="" />
QR + 2 < 2pq="" />
PQ > (QR + 2)/2
2. Substitute PR and PQ in terms of QR in the third equation:
PQ + QR + PR = 40
((QR + 2)/2) + QR + ((QR + 2)/2 + 10) = 40
3QR + 14 = 40
3QR = 26
QR = 8.67
3. Substitute QR into the first equation to find PQ:
PQ > (QR + 2)/2
PQ > (8.67 + 2)/2
PQ > 5.34
4. Substitute PQ and QR into the second equation to find PR:
PR = PQ + 10
PR = 5.34 + 10
PR = 15.34
5. Check that the sum of all sides is 40:
PQ + QR + PR = 5.34 + 8.67 + 15.34 = 29.35
6. Since PQ is the smallest side, the answer is 8 cm (rounded to the nearest whole number).
Therefore, the length of the smallest side of the triangle PQR is 8 cm.
- QR < 2pq="" -="" />
- PR = PQ + 10
- PQ + QR + PR = 40
To find:
The length of the smallest side of the triangle PQR.
Solution:
1. Simplify the first equation:
QR < 2pq="" -="" 2="" />
QR + 2 < 2pq="" />
PQ > (QR + 2)/2
2. Substitute PR and PQ in terms of QR in the third equation:
PQ + QR + PR = 40
((QR + 2)/2) + QR + ((QR + 2)/2 + 10) = 40
3QR + 14 = 40
3QR = 26
QR = 8.67
3. Substitute QR into the first equation to find PQ:
PQ > (QR + 2)/2
PQ > (8.67 + 2)/2
PQ > 5.34
4. Substitute PQ and QR into the second equation to find PR:
PR = PQ + 10
PR = 5.34 + 10
PR = 15.34
5. Check that the sum of all sides is 40:
PQ + QR + PR = 5.34 + 8.67 + 15.34 = 29.35
6. Since PQ is the smallest side, the answer is 8 cm (rounded to the nearest whole number).
Therefore, the length of the smallest side of the triangle PQR is 8 cm.
If the bisector of the angle A of a △ABC is perpendicular to the base BC of the triangle then the triangle ABC is :
- a)Obtuse Angled
- b)Isosceles
- c)Scalene
- d)Equilateral
Correct answer is option 'B'. Can you explain this answer?
If the bisector of the angle A of a △ABC is perpendicular to the base BC of the triangle then the triangle ABC is :
a)
Obtuse Angled
b)
Isosceles
c)
Scalene
d)
Equilateral

|
Imk Pathshala answered |
If the bisector of angle A of a triangle is perpendicular to the base BC of the triangle then the triangle ABC is:
B: Isosceles
Solution:
- The angle bisector of angle A divides the angle into two equal parts.
- For this bisector to be perpendicular to base BC, angles B and C must be equal.
- This means that triangle ABC has two equal sides opposite these equal angles.
- Therefore, triangle ABC is isosceles.
B: Isosceles
Solution:
- The angle bisector of angle A divides the angle into two equal parts.
- For this bisector to be perpendicular to base BC, angles B and C must be equal.
- This means that triangle ABC has two equal sides opposite these equal angles.
- Therefore, triangle ABC is isosceles.
If the altitudes from two vertices of a triangle to the opposite sides are equal, then the triangles is
- a)Scalene
- b)Isosceles
- c)Equilateral
- d)Right-angled
Correct answer is option 'B'. Can you explain this answer?
If the altitudes from two vertices of a triangle to the opposite sides are equal, then the triangles is
a)
Scalene
b)
Isosceles
c)
Equilateral
d)
Right-angled
|
|
Swati Verma answered |
Given:
BE = CD
Concept Used:
When 2 sides of a triangle are equal, then it is isosceles.
When 2 angles and 1 side of 2 triangles is equal, then both the triangles are similar.
Calculations:
In △ABE and △ACD,
BE = CD (Given)
∠BEA = ∠CDA (90° each)
∠BAE = ∠CAD (Common Angle)
∠ABE = ∠ACE (By Sum angle property)
⇒ △ABE is similar to △ACD
⇒ AB = AC
∴ If the altitudes from two vertices of a triangle to the opposite sides are equal, then the triangle is isosceles.
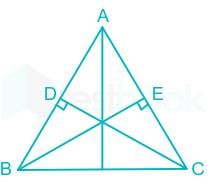
In the adjoining figure, the rule by which △ABC ≅ △ADC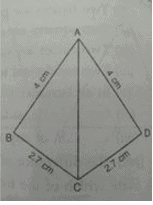
- a)AAS
- b)RHS
- c)SSS
- d)SAS
Correct answer is option 'C'. Can you explain this answer?
In the adjoining figure, the rule by which △ABC ≅ △ADC
a)
AAS
b)
RHS
c)
SSS
d)
SAS

|
Let's Tute answered |
In the given figure, we need to determine the rule by which ∆ABC is congruent to ∆ADC.
Observations:
- Side AC: This side is common to both triangles.
- Side AB = AD: Both sides are 4 cm.
- Side BC = CD: Both sides are 2.7 cm.
Rule for Congruence:
Since all three corresponding sides of the triangles are equal (AB = AD, BC = CD, AC = AC), the triangles satisfy the Side-Side-Side (SSS) congruence rule.
Correct Answer:
c) SSS
In the adjoining fig, PQ = PR. If ∠QPR = 48∘, then value of x is: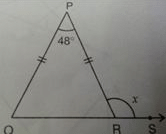
- a)114∘
- b)96∘
- c)132∘
- d)104∘
Correct answer is option 'A'. Can you explain this answer?
In the adjoining fig, PQ = PR. If ∠QPR = 48∘, then value of x is:
a)
114∘
b)
96∘
c)
132∘
d)
104∘

|
EduRev Class 9 answered |
- In triangle PQR, PQ = PR , making it an isosceles triangle.
- In an isosceles triangle, the angles opposite the equal sides are equal.
- Given angle QPR = 48 degrees ,
let angle PQR = angle PRQ = y
- The sum of angles in a triangle is 180.
- Therefore, y + y + 48 = 180
- Solving: 2y = 132 degrees
therefore y = 66 degrees
angle y + angle x = 180 degrees
66 + angle x = 180 degree
angle x = 180-66
angle x = 132 degree
In △ABC, AB=5 cm and BC=6 cm. Then, the length of AC cannot be- a)3.8 cm
- b)3.4 cm
- c)4cm
- d)3.6 cm
Correct answer is option 'B'. Can you explain this answer?
In △ABC, AB=5 cm and BC=6 cm. Then, the length of AC cannot be
a)
3.8 cm
b)
3.4 cm
c)
4cm
d)
3.6 cm
|
|
Ananya Das answered |
in triangle ABC
AB = 2.5 cm
BC = 6 cm
AC = ?
in any triangle sum of two sides > third side
=> AB + BC > AC
=> 2.5 + 6 > AC
=> AC < 8.5
AB + AC > BC
=> 2.5 + AC > 6
=> AC > 3.5
BC + AC > AB
=> 6 + AC > 2.5
=> AC > -3.5
Taking all together
3.5 < AC < 8.5
3.6 , 3.8 & 4 lies betwenn them
but not 3.4
Hence Length of AC can not be 3.4 cm
In the adjoining figure, BC = AD, CA⊥AB and BD⊥AB. The rule by which △ABC ≅ △BAD is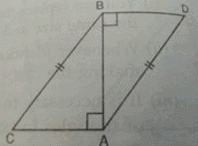
- a)ASA
- b)SAS
- c)RHS
- d)SSS
Correct answer is option 'C'. Can you explain this answer?
In the adjoining figure, BC = AD, CA⊥AB and BD⊥AB. The rule by which △ABC ≅ △BAD is
a)
ASA
b)
SAS
c)
RHS
d)
SSS

|
Sohan Mandal answered |
In ∆ABC and ∆BAD,
AB = common side
BC = AD ( given , side opposite to right angle of a
triangle is it's hypotenuse )
angle CAB = angle ABD( right angle )
therefore, ∆ABC and ∆BAD are congruent by RHS rule of congruence
AB = common side
BC = AD ( given , side opposite to right angle of a
triangle is it's hypotenuse )
angle CAB = angle ABD( right angle )
therefore, ∆ABC and ∆BAD are congruent by RHS rule of congruence
In △ABC, if ∠A = 45∘ and ∠B = 70∘, then the shortest and the longest sides of the triangle are respectively,- a)BC,AB
- b)AB,AC
- c)AB,BC
- d)BC,AC
Correct answer is option 'D'. Can you explain this answer?
In △ABC, if ∠A = 45∘ and ∠B = 70∘, then the shortest and the longest sides of the triangle are respectively,
a)
BC,AB
b)
AB,AC
c)
AB,BC
d)
BC,AC
|
|
Prateek Kushwaha answered |
We know . opposite side of longest angle is longer
so AC is longer side
and short angle is A
so opposite side BC is shorter side
so AC is longer side
and short angle is A
so opposite side BC is shorter side
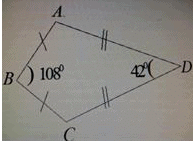
In figure, ABCD is a quadrilateral in which AB = BC and AD = DC. Measure of ∠BCD is:
- a)30∘
- b)72∘
- c)150∘
- d)105∘
Correct answer is option 'D'. Can you explain this answer?
In figure, ABCD is a quadrilateral in which AB = BC and AD = DC. Measure of ∠BCD is:
a)
30∘
b)
72∘
c)
150∘
d)
105∘

|
EduRev Class 9 answered |
In ΔABC ,as it is isoceles so,
∠BCA=36° [ (180°-108°)/2 ]
In ΔADC ,as it is isoceles so,
∠DCA=69° [ (180°-42°)/2 ]
∠BCD=∠BCA+∠DCA
∠BCD=36°+69°
∠BCD=105°
∠BCA=36° [ (180°-108°)/2 ]
In ΔADC ,as it is isoceles so,
∠DCA=69° [ (180°-42°)/2 ]
∠BCD=∠BCA+∠DCA
∠BCD=36°+69°
∠BCD=105°
In triangle PQR, PQ = PR and R = 65°, then P = ?
- a)75°
- b)50°
- c)40°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
In triangle PQR, PQ = PR and R = 65°, then P = ?
a)
75°
b)
50°
c)
40°
d)
120°
|
|
Gaurav Kumar answered |
By using the theorem,If two sides of a triangle are equal then the opposite angles to the sides are equal.
⇒ if PQ=PR then ∠Q=∠R
in triangle PQR,
⇒ ∠P+∠Q+∠R=180°
⇒ ∠P+∠Q+∠Q=180° (∵∠Q=∠R)
⇒ ∠P+65°+65°=180°
⇒ ∠P+130°=180°
⇒ ∠P=180°-130°
⇒ ∠P=50
⇒ if PQ=PR then ∠Q=∠R
in triangle PQR,
⇒ ∠P+∠Q+∠R=180°
⇒ ∠P+∠Q+∠Q=180° (∵∠Q=∠R)
⇒ ∠P+65°+65°=180°
⇒ ∠P+130°=180°
⇒ ∠P=180°-130°
⇒ ∠P=50
Two equilateral triangles are congruent when:
- a)Their areas are proportional
- b)Their sides are equal
- c)Their sides are proportional
- d)Their angles are equal
Correct answer is option 'B'. Can you explain this answer?
Two equilateral triangles are congruent when:
a)
Their areas are proportional
b)
Their sides are equal
c)
Their sides are proportional
d)
Their angles are equal

|
EduRev Class 9 answered |
Explanation: For two equilateral triangles to be congruent, their corresponding sides must be equal in length. In congruent triangles, all corresponding sides and angles are identical. While equilateral triangles always have equal angles (60°), congruence is specifically determined by the equality of sides.
Choose the correct statement- a)Two right triangles are congruent, if hypotenuse and a side of one are respectively equal to the hypotenuse and a side of the other triangle
- b)If thee altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles
- c)If any two sides of a right triangle are respectively are equal to two sides of the other right triangle, then the two triangles are congruent
- d)Sides opposite equal angles may be unequal
Correct answer is option 'A'. Can you explain this answer?
Choose the correct statement
a)
Two right triangles are congruent, if hypotenuse and a side of one are respectively equal to the hypotenuse and a side of the other triangle
b)
If thee altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles
c)
If any two sides of a right triangle are respectively are equal to two sides of the other right triangle, then the two triangles are congruent
d)
Sides opposite equal angles may be unequal

|
Let's Tute answered |
Answer: A
Explanation:
Option A is correct because the Hypotenuse-Side (HS) congruence criterion states that if the hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of another right triangle, the two triangles are congruent.
Option A is correct because the Hypotenuse-Side (HS) congruence criterion states that if the hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of another right triangle, the two triangles are congruent.
Other options are incorrect:
- B: This statement is partially correct but not universally true for all cases, as the altitude bisecting the opposite side guarantees an isosceles triangle only under specific conditions.
- C: The congruence of two right triangles cannot be guaranteed if just any two sides are equal; the Hypotenuse-Leg or another criterion must be specified.
- D: If the angles are equal, the opposite sides must also be equal, making this statement incorrect.
In the adjoining figure, ABCD is a quadrilateral in which AD = CB and AB = CD, then ∠ACB is equal to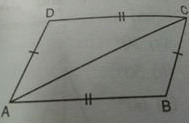
- a)∠CAD
- b)∠ACD
- c)∠BAD
- d)∠BAC
Correct answer is option 'A'. Can you explain this answer?
In the adjoining figure, ABCD is a quadrilateral in which AD = CB and AB = CD, then ∠ACB is equal to
a)
∠CAD
b)
∠ACD
c)
∠BAD
d)
∠BAC
|
|
Jiya Chandrapu answered |
The answer is a because , if we take them as alternate interior angles , then angle acb is equal to angle cad
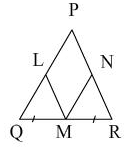
In isosceles ΔPQR, PQ = PR, M is the mid point of QR. LM ⊥ PQ, MN ⊥ PR. By which criterion of congruency is ΔQLM 0 ≅ ΔMNR.
- a)SAS
- b)RHS
- c)SSS
- d)AAS
Correct answer is option 'D'. Can you explain this answer?
In isosceles ΔPQR, PQ = PR, M is the mid point of QR. LM ⊥ PQ, MN ⊥ PR. By which criterion of congruency is ΔQLM 0 ≅ ΔMNR.
a)
SAS
b)
RHS
c)
SSS
d)
AAS

|
EduRev Class 9 answered |
∠LQ = ∠MNR,
∠Q = ∠R
QM = MR,
Hence, ΔQLM ≅ ΔMNR (by AAS)
It is not possible to construct a triangle when its sides are:- a)6 cm, 7 cm, 7 cm
- b)5.4 cm, 2.3 cm, 3 cm
- c)8.3 cm, 3.4 cm, 6.1 cm
- d)3 cm, 5 cm, 5 cm
Correct answer is option 'B'. Can you explain this answer?
It is not possible to construct a triangle when its sides are:
a)
6 cm, 7 cm, 7 cm
b)
5.4 cm, 2.3 cm, 3 cm
c)
8.3 cm, 3.4 cm, 6.1 cm
d)
3 cm, 5 cm, 5 cm
|
|
Dipika Chopra answered |
Explanation:
To construct a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. This is known as the triangle inequality theorem. Let's check each option:
a) 6 cm, 7 cm, 7 cm
- 6 + 7 > 7, 7 + 7 > 6, 6 + 7 > 7
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
b) 5.4 cm, 2.3 cm, 3 cm
- 5.4 + 2.3 < 3,="" 5.4="" +="" 3="" />< 2.3,="" 2.3="" +="" 3="" />< />
- The sum of the lengths of the two smaller sides is less than the length of the largest side, so it is not possible to construct a triangle with these side lengths.
c) 8.3 cm, 3.4 cm, 6.1 cm
- 8.3 + 3.4 > 6.1, 8.3 + 6.1 > 3.4, 3.4 + 6.1 > 8.3
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
d) 3 cm, 5 cm, 5 cm
- 3 + 5 > 5, 3 + 5 > 5, 5 + 5 > 3
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
Therefore, the correct answer is option B, as it is not possible to construct a triangle with side lengths 5.4 cm, 2.3 cm, and 3 cm.
To construct a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. This is known as the triangle inequality theorem. Let's check each option:
a) 6 cm, 7 cm, 7 cm
- 6 + 7 > 7, 7 + 7 > 6, 6 + 7 > 7
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
b) 5.4 cm, 2.3 cm, 3 cm
- 5.4 + 2.3 < 3,="" 5.4="" +="" 3="" />< 2.3,="" 2.3="" +="" 3="" />< />
- The sum of the lengths of the two smaller sides is less than the length of the largest side, so it is not possible to construct a triangle with these side lengths.
c) 8.3 cm, 3.4 cm, 6.1 cm
- 8.3 + 3.4 > 6.1, 8.3 + 6.1 > 3.4, 3.4 + 6.1 > 8.3
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
d) 3 cm, 5 cm, 5 cm
- 3 + 5 > 5, 3 + 5 > 5, 5 + 5 > 3
- The sum of any two sides is greater than the third side, so it is possible to construct a triangle with these side lengths.
Therefore, the correct answer is option B, as it is not possible to construct a triangle with side lengths 5.4 cm, 2.3 cm, and 3 cm.
In triangle ABC and triangle DEF, if AB/DE = AC/DF = BC/EF, then the triangles are:- a)Similar
- b)Congruent
- c)Isosceles
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
In triangle ABC and triangle DEF, if AB/DE = AC/DF = BC/EF, then the triangles are:
a)
Similar
b)
Congruent
c)
Isosceles
d)
None of the above

|
Vedha Thanu answered |
What is the valency for zinc chloric class 9
In triangles ABC and DEF, AB = FD and ∠A=∠D. The two triangles will be congruent by SAS axiom if :
- a)BC = EF
- b)AC = EF
- c)AC = DE
- d)BC = DE
Correct answer is option 'C'. Can you explain this answer?
In triangles ABC and DEF, AB = FD and ∠A=∠D. The two triangles will be congruent by SAS axiom if :
a)
BC = EF
b)
AC = EF
c)
AC = DE
d)
BC = DE
|
|
Hina Sharma answered |
BC = EF. The angles ∠ABC and ∠DEF are also congruent. Therefore, the triangles ABC and DEF are congruent by the Side-Angle-Side (SAS) congruence criterion.
In an isosceles right angled triangle, the measures of the acute angles are- a)40°, 50°
- b)35°, 55°
- c)45°, 45°
- d)60°, 30°
Correct answer is option 'C'. Can you explain this answer?
In an isosceles right angled triangle, the measures of the acute angles are
a)
40°, 50°
b)
35°, 55°
c)
45°, 45°
d)
60°, 30°
|
|
Anshika Rajput answered |
Bcz sum of all angles is 180 nd one is 90 ..also other two are equal as triangle is isoceles ...so .the angles are 45 nd 45
In the adjoining figure, AB = BC and ∠ABD = ∠CBD, then another angle which measures 30∘ is
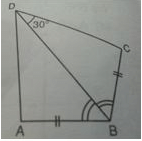
- a)∠BCD
- b)∠BDA
- c)∠BAD
- d)∠BCA
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, AB = BC and ∠ABD = ∠CBD, then another angle which measures 30∘ is

a)
∠BCD
b)
∠BDA
c)
∠BAD
d)
∠BCA
|
|
Pooja Shah answered |
The two triangles are congruent by SAS congruency.
D is a Point on the Side BC of a △ABC such that AD bisects ∠BAC then:- a)BD = CD
- b)CD > CA
- c)BD > BA
- d)BA > BD
Correct answer is option 'D'. Can you explain this answer?
D is a Point on the Side BC of a △ABC such that AD bisects ∠BAC then:
a)
BD = CD
b)
CD > CA
c)
BD > BA
d)
BA > BD
|
|
Sarita Reddy answered |
Correct, option 'D' is the correct answer.
When AD bisects ∠BAC, it means that angle BAC is split into two equal angles, BDA and BAC. Since BDA and BAC are equal, it means that angle BDA is half of angle BAC, and angle BAC is twice angle BDA.
Therefore, angle BAD is less than angle BAC.
As the angle BAC is greater than angle BAD, then it follows that side BA is greater than side BD.
Therefore, BA > BD.
In a triangle, the sum of the two smaller sides will always be greater than the largest side, which is called the triangle inequality theorem.
In the adjoining Figure, AB = AC and BD = CD. The ratio ∠ABD : ∠ACD is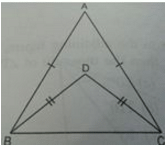
- a)It is 1 : 1
- b)It is 2 : 1
- c)It is 1 : 2
- d)It is 2 : 3
Correct answer is option 'A'. Can you explain this answer?
In the adjoining Figure, AB = AC and BD = CD. The ratio ∠ABD : ∠ACD is
a)
It is 1 : 1
b)
It is 2 : 1
c)
It is 1 : 2
d)
It is 2 : 3
|
|
Maroof Khan answered |
Because both angle line segments is equal
In ΔABC if AB = BC then:- a)∠A < ∠C
- b)∠C > ∠A
- c)∠A = ∠C
- d)∠B > ∠C
Correct answer is option 'C'. Can you explain this answer?
In ΔABC if AB = BC then:
a)
∠A < ∠C
b)
∠C > ∠A
c)
∠A = ∠C
d)
∠B > ∠C
|
|
Rochana Singh answered |
**Explanation:**
The given statement states that AB is equal to BC. Let's understand this statement and its implications in detail.
**Understanding the Statement:**
- AB = BC means the length of line segment AB is equal to the length of line segment BC.
- In simpler terms, the distance between point A and point B is the same as the distance between point B and point C.
**Implications:**
- If AB = BC, it implies that the triangle ABC is an isosceles triangle.
- An isosceles triangle is a triangle that has two sides of equal length.
- In this case, since AB = BC, the triangle ABC has two sides AB and BC that are equal.
- The third side AC can be of any length.
**Explanation of Options:**
a) A ≠ C: This option states that point A is not equal to point C. However, the given statement AB = BC does not provide any information about the equality of points A and C. So, this option is incorrect.
b) C ≠ A: This option states that point C is not equal to point A. Similar to the explanation for option a), the given statement AB = BC does not provide any information about the equality of points A and C. So, this option is incorrect.
c) A = C: This option states that point A is equal to point C. The given statement AB = BC does not directly mention anything about the equality of points A and C. However, since AB = BC, it implies that the two sides of the triangle ABC (AB and BC) are equal. And in an isosceles triangle, the angles opposite to the equal sides are also equal. So, angle A = angle C. Therefore, this option is correct.
d) B ≠ C: This option states that point B is not equal to point C. Similar to the explanation for option a), the given statement AB = BC does not provide any information about the equality of points B and C. So, this option is incorrect.
Therefore, the correct answer is option 'C' - A = C.
The given statement states that AB is equal to BC. Let's understand this statement and its implications in detail.
**Understanding the Statement:**
- AB = BC means the length of line segment AB is equal to the length of line segment BC.
- In simpler terms, the distance between point A and point B is the same as the distance between point B and point C.
**Implications:**
- If AB = BC, it implies that the triangle ABC is an isosceles triangle.
- An isosceles triangle is a triangle that has two sides of equal length.
- In this case, since AB = BC, the triangle ABC has two sides AB and BC that are equal.
- The third side AC can be of any length.
**Explanation of Options:**
a) A ≠ C: This option states that point A is not equal to point C. However, the given statement AB = BC does not provide any information about the equality of points A and C. So, this option is incorrect.
b) C ≠ A: This option states that point C is not equal to point A. Similar to the explanation for option a), the given statement AB = BC does not provide any information about the equality of points A and C. So, this option is incorrect.
c) A = C: This option states that point A is equal to point C. The given statement AB = BC does not directly mention anything about the equality of points A and C. However, since AB = BC, it implies that the two sides of the triangle ABC (AB and BC) are equal. And in an isosceles triangle, the angles opposite to the equal sides are also equal. So, angle A = angle C. Therefore, this option is correct.
d) B ≠ C: This option states that point B is not equal to point C. Similar to the explanation for option a), the given statement AB = BC does not provide any information about the equality of points B and C. So, this option is incorrect.
Therefore, the correct answer is option 'C' - A = C.
In ΔABC if ∠A = ∠B, then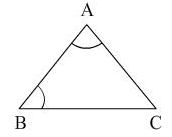
- a)AC ≠ BC
- b)AC = BC
- c)AB = AC
- d)AB = BC
Correct answer is option 'B'. Can you explain this answer?
In ΔABC if ∠A = ∠B, then
a)
AC ≠ BC
b)
AC = BC
c)
AB = AC
d)
AB = BC

|
Game Killer answered |
Becuase Sides opposite to equal angles are also equal.angle A = angle BBC is opposite to angle A and AC is opposite to angle B.Therefore, AC=BC in triangle ABC.
It is not possible to construct a triangle when the lengths of its sides are- a)4cm, 6cm, 6cm
- b)9.3cm, 5.2cm, 7.4cm
- c)6cm, 7cm, 8cm
- d)5.3cm, 2.2cm, 3.1cm
Correct answer is option 'D'. Can you explain this answer?
It is not possible to construct a triangle when the lengths of its sides are
a)
4cm, 6cm, 6cm
b)
9.3cm, 5.2cm, 7.4cm
c)
6cm, 7cm, 8cm
d)
5.3cm, 2.2cm, 3.1cm
|
|
Swati Verma answered |
For forming a triangle sum of any two sides must be greater than the third side.
In the adjoining figure, AB = AC and AD⊥BC. The rule by which △ABD ≅ △ACD is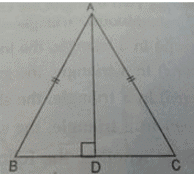
- a)SSS
- b)RHS
- c)SAS
- d)ASA
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, AB = AC and AD⊥BC. The rule by which △ABD ≅ △ACD is
a)
SSS
b)
RHS
c)
SAS
d)
ASA

|
Devansh Dalei answered |
SAS also may be applicable for this
The factor that causes a change in quantity demanded is- a)Price of the substitute good
- b)Price of the complementary good
- c)Price of the inputs
- d)Price of the given good
Correct answer is option 'D'. Can you explain this answer?
The factor that causes a change in quantity demanded is
a)
Price of the substitute good
b)
Price of the complementary good
c)
Price of the inputs
d)
Price of the given good

|
Deepa Sharma answered |
Correct option D. As there is inverse relation between quantity demanded and price.
In △ABC, ∠A = 35∘ and ∠B = 65∘, then the longest side of the triangle is:- a)AC
- b)BC
- c)AB
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In △ABC, ∠A = 35∘ and ∠B = 65∘, then the longest side of the triangle is:
a)
AC
b)
BC
c)
AB
d)
None of these
|
|
Atul Koyal answered |
Angle A is 35
Angle B is 65
Angle C will be 180-(35+65)
=180-100
=80
So angle C is the largest angle and as per the theorum the side opposite to larger angle is the largest.So side AB is the largest side.
Angle B is 65
Angle C will be 180-(35+65)
=180-100
=80
So angle C is the largest angle and as per the theorum the side opposite to larger angle is the largest.So side AB is the largest side.
In △ABC, if ∠B = 30∘ and ∠C = 70∘, then which of the following is the longest side?- a)AB
- b)BC
- c)AC
- d)AB or AC
Correct answer is option 'B'. Can you explain this answer?
In △ABC, if ∠B = 30∘ and ∠C = 70∘, then which of the following is the longest side?
a)
AB
b)
BC
c)
AC
d)
AB or AC
|
|
Prashansa Singh answered |
You are referring to a triangle, then the statement is incomplete. Please provide more information about the triangle and your question.
PQRS is a parallelogram, if the two diagonals are equal, then the measure of PQR is:- a)30°
- b)90°
- c)60°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
PQRS is a parallelogram, if the two diagonals are equal, then the measure of PQR is:
a)
30°
b)
90°
c)
60°
d)
120°

|
Imk Pathshala answered |
In a parallelogram, the diagonals are equal if and only if the parallelogram is a rectangle. This is because equal diagonals imply that the opposite angles are equal, and the only type of parallelogram where this happens is a rectangle.
In a rectangle, all angles are 90∘. Therefore, the measure of ∠PQR is: 90∘.
The altitude of an equilateral triangle of side a to any of its other sides from the opposite vertex is- a)
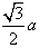
- b)
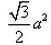
- c)
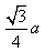
- d)
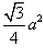
Correct answer is option 'A'. Can you explain this answer?
The altitude of an equilateral triangle of side a to any of its other sides from the opposite vertex is
a)
b)
c)
d)
|
|
Charming Rocky answered |
Option (a) is correct.. it can also be obtained by using Pythagoras theorem .. where base=a/2 and hypotenuse=a. .then altitude=. ...
In fig, AC = BC and ∠ACY = 140∘. Find X and Y:
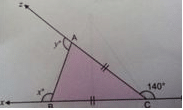
- a)95∘ and 150∘
- b)110∘ and 110∘
- c)50∘ and 120∘
- d)80∘ and 80∘
Correct answer is option 'B'. Can you explain this answer?
In fig, AC = BC and ∠ACY = 140∘. Find X and Y:
a)
95∘ and 150∘
b)
110∘ and 110∘
c)
50∘ and 120∘
d)
80∘ and 80∘

|
Imk Pathshala answered |
∠ACB = 40ο
as ABC is a isoceles trinagle
so ∠BAC = ∠ABC = a
a + a + 40 = 180ο
2a = 140ο
a = 70ο
x + a =180ο and y +a = 180ο
x = 110ο and y = 110ο
as ABC is a isoceles trinagle
so ∠BAC = ∠ABC = a
a + a + 40 = 180ο
2a = 140ο
a = 70ο
x + a =180ο and y +a = 180ο
x = 110ο and y = 110ο
Chapter doubts & questions for Triangles - Mathematics (Maths) Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Triangles - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|471 docs|57 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup