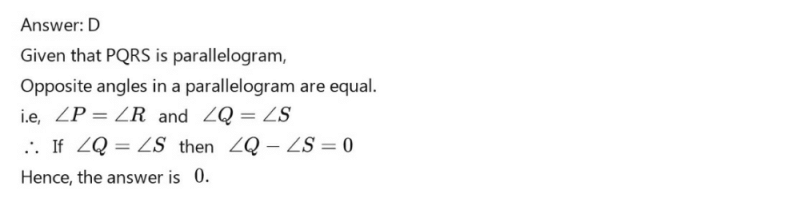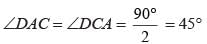All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Quadrilaterals for Class 9 Exam
In a parallelogram the sum of two consecutive angles is- a)360°
- b)100°
- c)180°
- d)90°
Correct answer is option 'C'. Can you explain this answer?
In a parallelogram the sum of two consecutive angles is
a)
360°
b)
100°
c)
180°
d)
90°
|
|
Maroof Khan answered |
Because sum of parallelogram is 180degree
Which of the following is not true for a parallelogram? - a)Diagonals bisect each other
- b)Opposite sides are equal
- c)Opposite angles are equal
- d)Opposite angles are bisected by the diagonals
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not true for a parallelogram?
a)
Diagonals bisect each other
b)
Opposite sides are equal
c)
Opposite angles are equal
d)
Opposite angles are bisected by the diagonals

|
Imk Pathshala answered |
The statement that opposite angles are bisected by the diagonals is not generally true. This property does not hold for every parallelogram; it only occurs in special cases such as a rectangle or a rhombus under certain conditions.
Thus, the option that is not always true for a parallelogram is:
Option D: Opposite angles are bisected by the diagonals.
Option D: Opposite angles are bisected by the diagonals.
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is a - a)Parallelogram
- b)Trapezium
- c)Rectangle
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is a
a)
Parallelogram
b)
Trapezium
c)
Rectangle
d)
None of these
|
|
Namrata Desai answered |
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is a Parallelogram.
Explanation:
A quadrilateral is a polygon with four sides. Let's consider a quadrilateral ABCD, where AB, BC, CD, and DA are the four sides.
Now, let's join the mid-points of the consecutive sides of the quadrilateral. Let the midpoints of AB, BC, CD, and DA be E, F, G, and H respectively.
To prove that the figure formed is a parallelogram, we need to show that opposite sides are parallel and equal in length.
1. Opposite sides are parallel:
- Join EF and GH. These diagonals divide the quadrilateral ABCD into four triangles: AEF, BFG, CGH, and DHG.
- By the Midpoint Theorem, EF is parallel to AB and GH is parallel to CD.
- Similarly, EG is parallel to AD and FH is parallel to BC.
- Therefore, opposite sides EF and GH are parallel, and opposite sides EG and FH are parallel.
2. Opposite sides are equal in length:
- By the Midpoint Theorem, EF = 1/2 AB and GH = 1/2 CD.
- Similarly, EG = 1/2 AD and FH = 1/2 BC.
- Therefore, opposite sides EF and GH are equal in length, and opposite sides EG and FH are equal in length.
Since the figure has opposite sides parallel and equal in length, it satisfies the definition of a parallelogram.
Hence, the figure formed by joining the mid-points of consecutive sides of a quadrilateral is a parallelogram.
Note: It is important to note that the converse of this statement is also true. That is, if a quadrilateral is a parallelogram, then the midpoints of its sides will form a parallelogram.
Explanation:
A quadrilateral is a polygon with four sides. Let's consider a quadrilateral ABCD, where AB, BC, CD, and DA are the four sides.
Now, let's join the mid-points of the consecutive sides of the quadrilateral. Let the midpoints of AB, BC, CD, and DA be E, F, G, and H respectively.
To prove that the figure formed is a parallelogram, we need to show that opposite sides are parallel and equal in length.
1. Opposite sides are parallel:
- Join EF and GH. These diagonals divide the quadrilateral ABCD into four triangles: AEF, BFG, CGH, and DHG.
- By the Midpoint Theorem, EF is parallel to AB and GH is parallel to CD.
- Similarly, EG is parallel to AD and FH is parallel to BC.
- Therefore, opposite sides EF and GH are parallel, and opposite sides EG and FH are parallel.
2. Opposite sides are equal in length:
- By the Midpoint Theorem, EF = 1/2 AB and GH = 1/2 CD.
- Similarly, EG = 1/2 AD and FH = 1/2 BC.
- Therefore, opposite sides EF and GH are equal in length, and opposite sides EG and FH are equal in length.
Since the figure has opposite sides parallel and equal in length, it satisfies the definition of a parallelogram.
Hence, the figure formed by joining the mid-points of consecutive sides of a quadrilateral is a parallelogram.
Note: It is important to note that the converse of this statement is also true. That is, if a quadrilateral is a parallelogram, then the midpoints of its sides will form a parallelogram.
ABCD is a ||gm and X, Y are the mid - points of sides AB and CD respectively, then- a)AXCY is rectangle
- b)AXCY is square
- c)AXCY is parallelogram
- d)AXCY is rhombus.
Correct answer is option 'C'. Can you explain this answer?
ABCD is a ||gm and X, Y are the mid - points of sides AB and CD respectively, then
a)
AXCY is rectangle
b)
AXCY is square
c)
AXCY is parallelogram
d)
AXCY is rhombus.
|
|
Meera Rana answered |
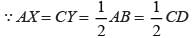

And also,
AB || CD, or AX || CY
∵ AX = CY and AX || CY
∴ AXCY is a ||gm
(∴ one pair of sides are equal and parallel)
In which of the following figures are the diagonals equal?- a)Rectangle
- b)Parallelogram
- c)Rhombus
- d)Trapezium
Correct answer is option 'A'. Can you explain this answer?
In which of the following figures are the diagonals equal?
a)
Rectangle
b)
Parallelogram
c)
Rhombus
d)
Trapezium
|
|
Sadhana Patel answered |
Diagonals in Different Figures:
In order to determine which of the given figures have equal diagonals, let's explore the properties of each figure.
a) Rectangle:
- A rectangle is a quadrilateral with four right angles.
- Opposite sides of a rectangle are parallel and congruent.
- Diagonals of a rectangle bisect each other, meaning they intersect at their midpoint.
- The diagonals of a rectangle are equal in length.
b) Parallelogram:
- A parallelogram is a quadrilateral with opposite sides that are parallel and congruent.
- The diagonals of a parallelogram bisect each other.
- However, the diagonals of a parallelogram are not necessarily equal in length.
c) Rhombus:
- A rhombus is a quadrilateral with all sides of equal length.
- Opposite sides of a rhombus are parallel.
- The diagonals of a rhombus bisect each other.
- Moreover, the diagonals of a rhombus are perpendicular to each other.
- The diagonals of a rhombus are not necessarily equal in length.
d) Trapezium:
- A trapezium is a quadrilateral with at least one pair of parallel sides.
- The diagonals of a trapezium do not necessarily bisect each other.
- Moreover, the diagonals of a trapezium are not necessarily equal in length.
Conclusion:
From the above analysis, we can conclude that the diagonals are equal in a rectangle but not in a parallelogram, rhombus, or trapezium. Therefore, the correct answer is option 'A' - Rectangle.
In order to determine which of the given figures have equal diagonals, let's explore the properties of each figure.
a) Rectangle:
- A rectangle is a quadrilateral with four right angles.
- Opposite sides of a rectangle are parallel and congruent.
- Diagonals of a rectangle bisect each other, meaning they intersect at their midpoint.
- The diagonals of a rectangle are equal in length.
b) Parallelogram:
- A parallelogram is a quadrilateral with opposite sides that are parallel and congruent.
- The diagonals of a parallelogram bisect each other.
- However, the diagonals of a parallelogram are not necessarily equal in length.
c) Rhombus:
- A rhombus is a quadrilateral with all sides of equal length.
- Opposite sides of a rhombus are parallel.
- The diagonals of a rhombus bisect each other.
- Moreover, the diagonals of a rhombus are perpendicular to each other.
- The diagonals of a rhombus are not necessarily equal in length.
d) Trapezium:
- A trapezium is a quadrilateral with at least one pair of parallel sides.
- The diagonals of a trapezium do not necessarily bisect each other.
- Moreover, the diagonals of a trapezium are not necessarily equal in length.
Conclusion:
From the above analysis, we can conclude that the diagonals are equal in a rectangle but not in a parallelogram, rhombus, or trapezium. Therefore, the correct answer is option 'A' - Rectangle.
The line segment joining the mid -points of the diagonals of a trapezium is- a)Parallel to the non-parallel sides
- b)Parallel to the parallel sides and equal ti the sum of the parallel sides.
- c)Parallel to the parallel sides and equal to the difference of the parallel sides.
- d)Parallel to the parallel sides, and , equal to half of the difference of the parallel sides.
Correct answer is option 'D'. Can you explain this answer?
The line segment joining the mid -points of the diagonals of a trapezium is
a)
Parallel to the non-parallel sides
b)
Parallel to the parallel sides and equal ti the sum of the parallel sides.
c)
Parallel to the parallel sides and equal to the difference of the parallel sides.
d)
Parallel to the parallel sides, and , equal to half of the difference of the parallel sides.

|
Nikhil Jain answered |
Understanding the Trapezium
A trapezium (or trapezoid) is a four-sided figure with at least one pair of parallel sides. Let's denote the parallel sides as 'a' and 'b', where 'a' is the longer side and 'b' is the shorter side.
Midpoints of the Diagonals
When we join the midpoints of the diagonals of a trapezium, we create a line segment. This segment has specific properties that relate to the trapezium's structure.
Properties of the Line Segment
- Parallelism: The line segment connecting the midpoints of the diagonals is always parallel to the parallel sides of the trapezium.
- Length: The length of this segment is equal to half of the difference of the lengths of the parallel sides. This means:
- If 'a' is the length of the longer parallel side and 'b' is the length of the shorter parallel side, then the length of the segment is given by (a - b)/2.
Conclusion
Therefore, the correct answer is option 'D': The line segment joining the midpoints of the diagonals of a trapezium is parallel to the parallel sides and equal to half of the difference of the parallel sides. This property can be useful in various geometrical problems and proofs involving trapeziums.
A trapezium (or trapezoid) is a four-sided figure with at least one pair of parallel sides. Let's denote the parallel sides as 'a' and 'b', where 'a' is the longer side and 'b' is the shorter side.
Midpoints of the Diagonals
When we join the midpoints of the diagonals of a trapezium, we create a line segment. This segment has specific properties that relate to the trapezium's structure.
Properties of the Line Segment
- Parallelism: The line segment connecting the midpoints of the diagonals is always parallel to the parallel sides of the trapezium.
- Length: The length of this segment is equal to half of the difference of the lengths of the parallel sides. This means:
- If 'a' is the length of the longer parallel side and 'b' is the length of the shorter parallel side, then the length of the segment is given by (a - b)/2.
Conclusion
Therefore, the correct answer is option 'D': The line segment joining the midpoints of the diagonals of a trapezium is parallel to the parallel sides and equal to half of the difference of the parallel sides. This property can be useful in various geometrical problems and proofs involving trapeziums.
In a quadrilateral, the angles are in the ratio 1 : 2 : 3 : 4. What is the value of largest angle?- a)108°
- b)144°
- c)136°
- d)124°
Correct answer is option 'B'. Can you explain this answer?
In a quadrilateral, the angles are in the ratio 1 : 2 : 3 : 4. What is the value of largest angle?
a)
108°
b)
144°
c)
136°
d)
124°
|
|
Nilofer Singh answered |
B)144
Let the four angles be 1x, 2x, 3x, and 4x respectively.
Since the sum of angles in a quadrilateral is 360 degrees, we have:
1x + 2x + 3x + 4x = 360
10x = 360
x = 36
Therefore, the largest angle is 4x = 4(36) = 144 degrees.
Let the four angles be 1x, 2x, 3x, and 4x respectively.
Since the sum of angles in a quadrilateral is 360 degrees, we have:
1x + 2x + 3x + 4x = 360
10x = 360
x = 36
Therefore, the largest angle is 4x = 4(36) = 144 degrees.
If the length of each side of rhombus is 15 cm and one of its diagonals is 24 cm what is length of other diagonal?- a)16 cm
- b)14 cm
- c)18 cm
- d)12 cm
Correct answer is option 'C'. Can you explain this answer?
If the length of each side of rhombus is 15 cm and one of its diagonals is 24 cm what is length of other diagonal?
a)
16 cm
b)
14 cm
c)
18 cm
d)
12 cm
|
|
Prachi Sharma answered |
Given information:
- Length of each side of the rhombus = 15 cm
- Length of one diagonal = 24 cm
To find: Length of the other diagonal
Properties of a rhombus:
1. All sides of a rhombus are equal in length.
2. The diagonals of a rhombus bisect each other at right angles.
Using these properties, we can solve the problem.
Solution:
Let's denote the length of the other diagonal as 'd'.
Step 1: Find the length of the other side of the rhombus.
Since all sides of a rhombus are equal in length, the length of each side is 15 cm.
Step 2: Find the length of the diagonals.
The diagonals of a rhombus bisect each other at right angles. This means that they divide the rhombus into four congruent right-angled triangles.
Using the Pythagorean theorem, we can find the length of the diagonals.
In each right-angled triangle, the hypotenuse is the length of the diagonal, and the two legs are the lengths of the sides of the rhombus.
Applying the Pythagorean theorem:
(15/2)^2 + (d/2)^2 = (24/2)^2
225/4 + d^2/4 = 144
225 + d^2 = 576
d^2 = 576 - 225
d^2 = 351
Taking the square root of both sides:
d = √351
d ≈ 18.7 cm (rounded to the nearest tenth)
Step 3: Choose the correct option.
The question asks for the length of the other diagonal, so the answer is approximately 18.7 cm, which is closest to option (c) 18 cm.
Therefore, the correct answer is option (c) 18 cm.
- Length of each side of the rhombus = 15 cm
- Length of one diagonal = 24 cm
To find: Length of the other diagonal
Properties of a rhombus:
1. All sides of a rhombus are equal in length.
2. The diagonals of a rhombus bisect each other at right angles.
Using these properties, we can solve the problem.
Solution:
Let's denote the length of the other diagonal as 'd'.
Step 1: Find the length of the other side of the rhombus.
Since all sides of a rhombus are equal in length, the length of each side is 15 cm.
Step 2: Find the length of the diagonals.
The diagonals of a rhombus bisect each other at right angles. This means that they divide the rhombus into four congruent right-angled triangles.
Using the Pythagorean theorem, we can find the length of the diagonals.
In each right-angled triangle, the hypotenuse is the length of the diagonal, and the two legs are the lengths of the sides of the rhombus.
Applying the Pythagorean theorem:
(15/2)^2 + (d/2)^2 = (24/2)^2
225/4 + d^2/4 = 144
225 + d^2 = 576
d^2 = 576 - 225
d^2 = 351
Taking the square root of both sides:
d = √351
d ≈ 18.7 cm (rounded to the nearest tenth)
Step 3: Choose the correct option.
The question asks for the length of the other diagonal, so the answer is approximately 18.7 cm, which is closest to option (c) 18 cm.
Therefore, the correct answer is option (c) 18 cm.
The figure formed by joining the mid-points of the adjacent sides of a square is - a)Parallelogram
- b)Rectangle
- c)Rhombus
- d)Square
Correct answer is option 'D'. Can you explain this answer?
The figure formed by joining the mid-points of the adjacent sides of a square is
a)
Parallelogram
b)
Rectangle
c)
Rhombus
d)
Square
|
|
Samarth Rane answered |
Explanation:
To understand why the figure formed by joining the mid-points of the adjacent sides of a square is a square, let's consider a square ABCD.
Definition:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
Construction:
- Let P, Q, R, and S be the midpoints of AB, BC, CD, and DA respectively.
- Join PQ, QR, RS, and SP.
Proof:
- To prove that the figure formed by joining the mid-points of the adjacent sides of a square is a square, we need to show that all four sides are equal in length and all four angles are equal to 90 degrees.
All four sides are equal in length:
- In a square ABCD, all four sides are equal. Therefore, AB = BC = CD = DA.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we have PQ || AB, QR || BC, RS || CD, and SP || DA.
- By the midpoint theorem, we know that PQ = QR = RS = SP.
- Therefore, all four sides of the figure formed by joining the mid-points are equal in length.
All four angles are equal to 90 degrees:
- In a square ABCD, all four angles are equal to 90 degrees.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we can see that PQ is parallel to AB and QR is parallel to BC.
- Since AB and BC are perpendicular to each other, PQ and QR are also perpendicular to each other.
- Similarly, RS is perpendicular to CD and SP is perpendicular to DA.
- Therefore, all four angles of the figure formed by joining the mid-points are equal to 90 degrees.
Conclusion:
- Since all four sides of the figure formed by joining the mid-points of the adjacent sides of a square are equal in length and all four angles are equal to 90 degrees, the figure is a square.
- Hence, option 'D', square, is the correct answer.
To understand why the figure formed by joining the mid-points of the adjacent sides of a square is a square, let's consider a square ABCD.
Definition:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
Construction:
- Let P, Q, R, and S be the midpoints of AB, BC, CD, and DA respectively.
- Join PQ, QR, RS, and SP.
Proof:
- To prove that the figure formed by joining the mid-points of the adjacent sides of a square is a square, we need to show that all four sides are equal in length and all four angles are equal to 90 degrees.
All four sides are equal in length:
- In a square ABCD, all four sides are equal. Therefore, AB = BC = CD = DA.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we have PQ || AB, QR || BC, RS || CD, and SP || DA.
- By the midpoint theorem, we know that PQ = QR = RS = SP.
- Therefore, all four sides of the figure formed by joining the mid-points are equal in length.
All four angles are equal to 90 degrees:
- In a square ABCD, all four angles are equal to 90 degrees.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we can see that PQ is parallel to AB and QR is parallel to BC.
- Since AB and BC are perpendicular to each other, PQ and QR are also perpendicular to each other.
- Similarly, RS is perpendicular to CD and SP is perpendicular to DA.
- Therefore, all four angles of the figure formed by joining the mid-points are equal to 90 degrees.
Conclusion:
- Since all four sides of the figure formed by joining the mid-points of the adjacent sides of a square are equal in length and all four angles are equal to 90 degrees, the figure is a square.
- Hence, option 'D', square, is the correct answer.
ABCD is a parallelogram in which the bisectors of angles ∠A and ∠B intersect at point P then ∠APB is
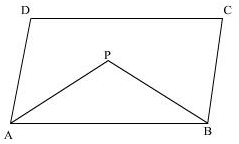
- a)45°
- b)90°
- c)60°
- d)80°
Correct answer is option 'B'. Can you explain this answer?
ABCD is a parallelogram in which the bisectors of angles ∠A and ∠B intersect at point P then ∠APB is
a)
45°
b)
90°
c)
60°
d)
80°

|
Imk Pathshala answered |
Since ABCD is a Parallelogram. Therefore,
AD || BC
AB is a transversal . Therefore ,
A + B = 180°. [ Consecutive interior angles]
Multiply both sides by 1/2 ,
1/2 A + 1/2 B = 1/2 (180°)
1/2 A + 1/2 B = 90° __【1】
Since, AP and PB are angle bisectors of A and B . Therefore,
Angle 1 = 1/2 A
Angle 2 = 1/2 B
Substitute the values in【1】,
Angle 1 + Angle 2 = 90°____【2】
Now, in ∆ APB,
1 + APB + 2 = 180°
90° + APB = 180°. [From 【2】]
APB = 90°
- HENCE PROVED
AD || BC
AB is a transversal . Therefore ,
A + B = 180°. [ Consecutive interior angles]
Multiply both sides by 1/2 ,
1/2 A + 1/2 B = 1/2 (180°)
1/2 A + 1/2 B = 90° __【1】
Since, AP and PB are angle bisectors of A and B . Therefore,
Angle 1 = 1/2 A
Angle 2 = 1/2 B
Substitute the values in【1】,
Angle 1 + Angle 2 = 90°____【2】
Now, in ∆ APB,
1 + APB + 2 = 180°
90° + APB = 180°. [From 【2】]
APB = 90°
- HENCE PROVED
ABCD is a parallelogram in which W, X, Y, Z are mid - points of sides AB, BC, CD and DA respectively. AC is the diagonal, then which of the following is correct?- a)YZ = AC
- b)YZ = 1/2
- c)YZ = 2/4
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
ABCD is a parallelogram in which W, X, Y, Z are mid - points of sides AB, BC, CD and DA respectively. AC is the diagonal, then which of the following is correct?
a)
YZ = AC
b)
YZ = 1/2
c)
YZ = 2/4
d)
None of these
|
|
Sagar Menon answered |
Understanding the Parallelogram ABCD
In the parallelogram ABCD, we have midpoints W, X, Y, and Z on sides AB, BC, CD, and DA respectively. The points W, X, Y, and Z form a new quadrilateral, which has some interesting properties.
Properties of Midpoints in a Parallelogram
- In any quadrilateral, the segment connecting the midpoints of two sides is parallel to the third side and half its length.
- The line segment connecting midpoints Y and Z (YZ) will be parallel to the diagonal AC and half its length.
Finding the Length of YZ
- Since Y and Z are the midpoints of sides CD and DA respectively, YZ is parallel to AC.
- By the property of midpoints in a parallelogram, we know that YZ = 1/2 * AC.
Conclusion
- Therefore, YZ = 1/2 AC is the correct relation.
- This means that option 'b' (YZ = 1/2 AC) is indeed correct.
In summary, when considering the midpoints of the sides of a parallelogram, the segment connecting these midpoints will be half the length of the diagonal it is parallel to. Thus, it is confirmed that YZ = 1/2 AC.
In the parallelogram ABCD, we have midpoints W, X, Y, and Z on sides AB, BC, CD, and DA respectively. The points W, X, Y, and Z form a new quadrilateral, which has some interesting properties.
Properties of Midpoints in a Parallelogram
- In any quadrilateral, the segment connecting the midpoints of two sides is parallel to the third side and half its length.
- The line segment connecting midpoints Y and Z (YZ) will be parallel to the diagonal AC and half its length.
Finding the Length of YZ
- Since Y and Z are the midpoints of sides CD and DA respectively, YZ is parallel to AC.
- By the property of midpoints in a parallelogram, we know that YZ = 1/2 * AC.
Conclusion
- Therefore, YZ = 1/2 AC is the correct relation.
- This means that option 'b' (YZ = 1/2 AC) is indeed correct.
In summary, when considering the midpoints of the sides of a parallelogram, the segment connecting these midpoints will be half the length of the diagonal it is parallel to. Thus, it is confirmed that YZ = 1/2 AC.
The perimeter of a parallelogram is 24 cm. If the longer side measures 8 cm. Then what is the measure of shroter side?- a)4 cm
- b)6 cm
- c)2 cm
- d)None of There
Correct answer is option 'A'. Can you explain this answer?
The perimeter of a parallelogram is 24 cm. If the longer side measures 8 cm. Then what is the measure of shroter side?
a)
4 cm
b)
6 cm
c)
2 cm
d)
None of There
|
|
Shilpa Choudhury answered |
Perimeter of ||gm = 2(a + b) = 24 cm
⇒ a + b = 12 cm
Given a = 8 cm
then 8 + b = 12 cm
⇒ b = 4 cm
⇒ a + b = 12 cm
Given a = 8 cm
then 8 + b = 12 cm
⇒ b = 4 cm
The resulting figure obtained from joining the consecutive mid points of side of a square is- a)Rectangle
- b)Square
- c)Trapezium
- d)Rhombus
Correct answer is option 'B'. Can you explain this answer?
The resulting figure obtained from joining the consecutive mid points of side of a square is
a)
Rectangle
b)
Square
c)
Trapezium
d)
Rhombus

|
Prerna Chavan answered |
There are several ways to approach this problem, but one of the most straightforward methods is to draw a square and label its sides and midpoints. Let's go through the solution step by step.
Step 1: Draw a square
Start by drawing a square with all sides of equal length. Label the four corners as A, B, C, and D.
Step 2: Label the midpoints
Next, label the midpoints of each side of the square. Let's call the midpoint on AB as E, BC as F, CD as G, and DA as H.
Step 3: Join the midpoints
Now, join the midpoints consecutively. That is, join E and F, F and G, G and H, and finally, H and E.
Step 4: Observe the resulting figure
Take a moment to observe the resulting figure formed by joining the consecutive midpoints. You will notice that it is a smaller square inside the original square.
Step 5: Identify the shape
Based on our observation, we can conclude that the resulting figure obtained from joining the consecutive midpoints of the sides of a square is another square. Therefore, the correct answer is option 'B' - Square.
Explanation:
When we join the consecutive midpoints of the sides of a square, we are essentially connecting the midpoints of each side. This creates a smaller square inside the original square. This smaller square shares the same center and orientation as the original square, but its sides are shorter in length. Therefore, the resulting figure is another square. This can be proven mathematically as well using properties of similar triangles and the fact that the diagonals of a square bisect each other at right angles.
In conclusion, the correct answer is option 'B' - Square.
Step 1: Draw a square
Start by drawing a square with all sides of equal length. Label the four corners as A, B, C, and D.
Step 2: Label the midpoints
Next, label the midpoints of each side of the square. Let's call the midpoint on AB as E, BC as F, CD as G, and DA as H.
Step 3: Join the midpoints
Now, join the midpoints consecutively. That is, join E and F, F and G, G and H, and finally, H and E.
Step 4: Observe the resulting figure
Take a moment to observe the resulting figure formed by joining the consecutive midpoints. You will notice that it is a smaller square inside the original square.
Step 5: Identify the shape
Based on our observation, we can conclude that the resulting figure obtained from joining the consecutive midpoints of the sides of a square is another square. Therefore, the correct answer is option 'B' - Square.
Explanation:
When we join the consecutive midpoints of the sides of a square, we are essentially connecting the midpoints of each side. This creates a smaller square inside the original square. This smaller square shares the same center and orientation as the original square, but its sides are shorter in length. Therefore, the resulting figure is another square. This can be proven mathematically as well using properties of similar triangles and the fact that the diagonals of a square bisect each other at right angles.
In conclusion, the correct answer is option 'B' - Square.
Two opposite angles of a parallelogram are (3x - 2)° and (50 - x)°. Find the smallest angle.- a)37°
- b)43°
- c)47°
- d)57°
Correct answer is option 'A'. Can you explain this answer?
Two opposite angles of a parallelogram are (3x - 2)° and (50 - x)°. Find the smallest angle.
a)
37°
b)
43°
c)
47°
d)
57°
|
|
Shilpa Choudhury answered |
∵ The opposite angles of a parallelogram are equal.
∴ (3x-2)° = (50 -x)°
⇒ 4x = 52°
⇒ x = 13°
∴ (3x - 2)° = 37°
∴ (50 - x)° = 37°
∴ (3x-2)° = (50 -x)°
⇒ 4x = 52°
⇒ x = 13°
∴ (3x - 2)° = 37°
∴ (50 - x)° = 37°
If an angle of a parallelogram is two third of its adjacent angle what is the measure of smallest angle of parallelogram?- a)81°
- b)72°
- c)54°
- d)108°
Correct answer is option 'B'. Can you explain this answer?
If an angle of a parallelogram is two third of its adjacent angle what is the measure of smallest angle of parallelogram?
a)
81°
b)
72°
c)
54°
d)
108°
|
|
Shilpa Choudhury answered |
Let the angle be x°
∴ Its adjacent angle = (180 - x)°
A/Q,
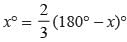
⇒ 3x° = 360° - 2x°
⇒ 5x = 360°
⇒ x = 72°
∴ Its adjacent angle = (180 - x)°
A/Q,
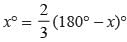
⇒ 3x° = 360° - 2x°
⇒ 5x = 360°
⇒ x = 72°
In ΔABC, AD is the median through A and E is the mid-point of AD. BE produced meets AC in F. then which of the following is correct?

- a)

- b)

- c)

- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In ΔABC, AD is the median through A and E is the mid-point of AD. BE produced meets AC in F. then which of the following is correct?


a)

b)

c)

d)
None of these
|
|
Rohit Sharma answered |
∵ AD is the median of ΔABC
∴ BD = DC
Through D, draw DR || BF

Now, in ΔBFC,
DR || BF and D is the mid-point of BC
∴ R should be the mid-point of FC (according to converse of mid-point theorem)
∴ FR = RC ...(i)
Similarly, in ΔADR
E is the mid-point of AD and EF || DR
∴ F should be the mid-point of AR
∴ FR = AF ...(ii)
Using (i) and (ii)
FR = RC = AF
⇒ AC = 3AF
⇒
∴ BD = DC
Through D, draw DR || BF

Now, in ΔBFC,
DR || BF and D is the mid-point of BC
∴ R should be the mid-point of FC (according to converse of mid-point theorem)
∴ FR = RC ...(i)
Similarly, in ΔADR
E is the mid-point of AD and EF || DR
∴ F should be the mid-point of AR
∴ FR = AF ...(ii)
Using (i) and (ii)
FR = RC = AF
⇒ AC = 3AF
⇒

Which of the following statements is true about the diagonal of a parallelogram?- a)A diagonal of a parallelogram divides it into two congruent triangles.
- b)A diagonal of a parallelogram divides it into two unequal triangles.
- c)A diagonal of a parallelogram does not divide it into triangles.
- d)A diagonal of a parallelogram always forms an isosceles triangle.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements is true about the diagonal of a parallelogram?
a)
A diagonal of a parallelogram divides it into two congruent triangles.
b)
A diagonal of a parallelogram divides it into two unequal triangles.
c)
A diagonal of a parallelogram does not divide it into triangles.
d)
A diagonal of a parallelogram always forms an isosceles triangle.

|
EduRev Class 9 answered |
Answer: A
Solution:
A diagonal of a parallelogram divides the parallelogram into two congruent triangles. This is a fundamental property of parallelograms as stated in Theorem 8.1.
Correct Answer: (A) A diagonal of a parallelogram divides it into two congruent triangles.
Solution:
A diagonal of a parallelogram divides the parallelogram into two congruent triangles. This is a fundamental property of parallelograms as stated in Theorem 8.1.
Correct Answer: (A) A diagonal of a parallelogram divides it into two congruent triangles.
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. What is the sum of largest and smallest angle of quadrilateral? - a)168°
- b)192°
- c)144°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. What is the sum of largest and smallest angle of quadrilateral?
a)
168°
b)
192°
c)
144°
d)
None of these
|
|
Swati Verma answered |
Let the angles be 3x,5x,9x and 13x
∴ Sum of largest and smallest angle = 3x + 13x = 16x
A/Q,
3x + 5x + 9x + 13x = 360°
⇒ 30x = 360° ⇒ x = 12
∴ 16x = 16 × 12° = 192°
∴ Sum of largest and smallest angle = 3x + 13x = 16x
A/Q,
3x + 5x + 9x + 13x = 360°
⇒ 30x = 360° ⇒ x = 12
∴ 16x = 16 × 12° = 192°
In a triangle, the line segment joining the midpoints of two sides has which of the following properties?- a)It is perpendicular to the third side.
- b)It is equal in length to the third side.
- c)It is parallel to the third side and half of its length.
- d)It divides the triangle into two congruent triangles.
Correct answer is option 'C'. Can you explain this answer?
In a triangle, the line segment joining the midpoints of two sides has which of the following properties?
a)
It is perpendicular to the third side.
b)
It is equal in length to the third side.
c)
It is parallel to the third side and half of its length.
d)
It divides the triangle into two congruent triangles.

|
Imk Pathshala answered |
Answer: C
Solution:
In a triangle, if a line segment joins the midpoints of two sides, it is parallel to the third side and half of its length. This is derived from the property of midpoints and parallelograms formed in the figure.
Correct Answer: (C) It is parallel to the third side and half of its length.
Solution:
In a triangle, if a line segment joins the midpoints of two sides, it is parallel to the third side and half of its length. This is derived from the property of midpoints and parallelograms formed in the figure.
Correct Answer: (C) It is parallel to the third side and half of its length.
Which of the following statements correctly proves that each angle of a rectangle is a right angle?- a)Opposite angles of a rectangle are supplementary.
- b)Interior angles on the same side of a transversal in a rectangle are always 90°.
- c)A rectangle is a parallelogram where one angle is a right angle, and all opposite and adjacent angles are equal to 90°.
- d)A rectangle does not follow the property of a parallelogram.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements correctly proves that each angle of a rectangle is a right angle?
a)
Opposite angles of a rectangle are supplementary.
b)
Interior angles on the same side of a transversal in a rectangle are always 90°.
c)
A rectangle is a parallelogram where one angle is a right angle, and all opposite and adjacent angles are equal to 90°.
d)
A rectangle does not follow the property of a parallelogram.

|
Imk Pathshala answered |
Answer: C
Solution:
A rectangle is a parallelogram where one angle is a right angle (90 degrees). Using the properties of parallelograms:
Solution:
A rectangle is a parallelogram where one angle is a right angle (90 degrees). Using the properties of parallelograms:
- Interior angles on the same side of the transversal add up to 180 degrees
- Opposite angles are equal.
Since one angle is 90 degrees , all other angles (∠B,∠C,∠D) are also 90 degrees
Correct Answer: (C) A rectangle is a parallelogram where one angle is a right angle, and all opposite and adjacent angles are equal to 90°.
Correct Answer: (C) A rectangle is a parallelogram where one angle is a right angle, and all opposite and adjacent angles are equal to 90°.
The angles of a quadrilateral are 98°, 92°,70° respectively. What is the measure of 4th angle? - a)92°
- b)98°
- c)100°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The angles of a quadrilateral are 98°, 92°,70° respectively. What is the measure of 4th angle?
a)
92°
b)
98°
c)
100°
d)
None of these
|
|
Shilpa Choudhury answered |
Let the measure of 4th angle be x°
∴ 98° + 92° +70° + x° = 180° × 2 = 360°
⇒ x° = 100°
∴ 98° + 92° +70° + x° = 180° × 2 = 360°
⇒ x° = 100°
D is the mid-point of side AB of a parallelogram ABCD. A line through B parallel to PD meets DC at Q and AD produced at R, then which of the following is correct?- a)AR = BC
- b)
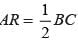
- c)AR = 2BC
- d)AR = 3BC
Correct answer is option 'C'. Can you explain this answer?
D is the mid-point of side AB of a parallelogram ABCD. A line through B parallel to PD meets DC at Q and AD produced at R, then which of the following is correct?
a)
AR = BC
b)
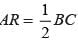
c)
AR = 2BC
d)
AR = 3BC
|
|
Shilpa Choudhury answered |
In DABR
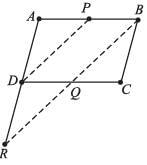
DP ∥ BR, and P is the mid-point of side AB
∴ Using mid-point theorem (converse) Point P is the mid - point of AB and is parallel to BR.
∴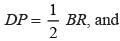
D will be the mid -point of side AR
∴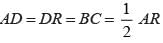
⇒ AR = 2BC

DP ∥ BR, and P is the mid-point of side AB
∴ Using mid-point theorem (converse) Point P is the mid - point of AB and is parallel to BR.
∴
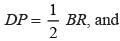
D will be the mid -point of side AR
∴
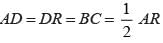
⇒ AR = 2BC
AN and CP are perpendiculars to the diagonal BD of a parallelogram ABCD. Choose the correct option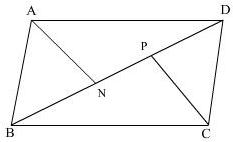
- a)AN ≠ CP
- b)AN > CP
- c)AN < CP
- d)AN = CP
Correct answer is option 'D'. Can you explain this answer?
AN and CP are perpendiculars to the diagonal BD of a parallelogram ABCD. Choose the correct option
a)
AN ≠ CP
b)
AN > CP
c)
AN < CP
d)
AN = CP

|
EduRev Class 9 answered |
Here, AN and CP are perpendiculars dropped from points A and C, respectively, to the diagonal BD of the parallelogram ABCD.
From properties of parallelograms and the perpendiculars drawn from vertices to the diagonal, it can be concluded that the two perpendiculars AN and CP must be equal in length. This is because in any parallelogram, the perpendicular distances from opposite vertices to the diagonal are always equal.
Thus, the correct option is: d) AN = CP
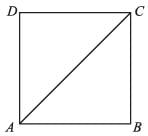
ABCD is a square. What is the value of ∠ACD ?
- a)40°
- b)45°
- c)50°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
ABCD is a square. What is the value of ∠ACD ?


a)
40°
b)
45°
c)
50°
d)
30°
|
|
Shilpa Choudhury answered |
∵ ABCD is a square
∴ ∠D = 90° and AD = DC = AB = BC In DADC
AD = DC
∴ ∠CAD = ∠ACD, and
∠D + ∠ACD + ∠CAD = 180°
⇒ 90° + 2 ∠ACD = 180°
⇒ ∠ACD =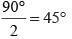
∴ ∠D = 90° and AD = DC = AB = BC In DADC
AD = DC
∴ ∠CAD = ∠ACD, and
∠D + ∠ACD + ∠CAD = 180°
⇒ 90° + 2 ∠ACD = 180°
⇒ ∠ACD =
If consecutive sides of a parallelogram are equal then it is a (none of the angle ≠ 90°)- a)Kite
- b)Rectangle
- c)Rhombus
- d)Square
Correct answer is option 'C'. Can you explain this answer?
If consecutive sides of a parallelogram are equal then it is a (none of the angle ≠ 90°)
a)
Kite
b)
Rectangle
c)
Rhombus
d)
Square
|
|
Swati Verma answered |
Rhombus is a parallelogram having consecutive sides equal and none of the angles equal a right angle.
The angles of a quadrilateral are in the ratio 2:4:5:7. What is the difference between largest and smallest angle? - a)80°
- b)100°
- c)60°
- d)90°
Correct answer is option 'B'. Can you explain this answer?
The angles of a quadrilateral are in the ratio 2:4:5:7. What is the difference between largest and smallest angle?
a)
80°
b)
100°
c)
60°
d)
90°
|
|
Shilpa Choudhury answered |
Let the angles be 2x, 4x,5x and 7x respectively.
∴ Difference between largest and smallest angle = lx - 2x = 5x
∵ Sum of all angles of a quadrilateral = 360°
⇒ 2x + 4x + 5x + lx = 360°
⇒ 18x=360°
⇒ x = 20°
∴ Required difference
= 7x - 2x = 5x
= 5 x 20° = 100°
∴ Difference between largest and smallest angle = lx - 2x = 5x
∵ Sum of all angles of a quadrilateral = 360°
⇒ 2x + 4x + 5x + lx = 360°
⇒ 18x=360°
⇒ x = 20°
∴ Required difference
= 7x - 2x = 5x
= 5 x 20° = 100°
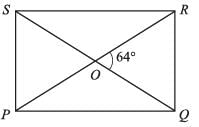
The diagonals of a rectangle PQRS meet at O. If ∠SOR = 64° then Find ∠OAC ?
- a)60°
- b)58°
- c)62°
- d)64°
Correct answer is option 'B'. Can you explain this answer?
The diagonals of a rectangle PQRS meet at O. If ∠SOR = 64° then Find ∠OAC ?


a)
60°
b)
58°
c)
62°
d)
64°
|
|
Shilpa Choudhury answered |
∵ Diagonals of a rectangle bisect each other and are also equal in length.
∴ In DPOS,
OP = OS
⇒ ∠OPS = ∠OSP
(angles opposite to equal sides are equal)
Also,
∠POS + ∠OSP + ∠OPS = 180°
⇒ 2∠OPS = 180° - ∠POS
= 180° - 64° (∵ ∠POS + ∠QOR) {vertically opposite∠s}
⇒
∴ In DPOS,
OP = OS
⇒ ∠OPS = ∠OSP
(angles opposite to equal sides are equal)
Also,
∠POS + ∠OSP + ∠OPS = 180°
⇒ 2∠OPS = 180° - ∠POS
= 180° - 64° (∵ ∠POS + ∠QOR) {vertically opposite∠s}
⇒

Chapter doubts & questions for Quadrilaterals - Mathematics (Maths) Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadrilaterals - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|471 docs|57 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily