Class 9 Exam > Class 9 Questions > The figure formed by joining the mid-points o...
Start Learning for Free
The figure formed by joining the mid-points of the adjacent sides of a square is
- a)Parallelogram
- b)Rectangle
- c)Rhombus
- d)Square
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The figure formed by joining the mid-points of the adjacent sides of a...
P, Q, R and S are the mid-points of BA, BC, CD and DA respectively.
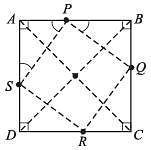
∴ AP = AS = PB = BQ = QC
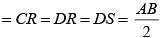
∴ In ΔAPS
AP = AS

Similarly
Similarly ∠ASP = ∠APS =∠BPQ = ∠BQP = ∠CQR
= ∠CRQ = ∠DSR = ∠DRS = 45°
Now ∠P + ∠ASP + ∠APS = 180°
⇒ ∠P = 90°
Similarly,
∠P = ∠Q = ∠R = ∠S = 90°
∴ PQRS is a parallelogram having each of its angles = 90°
Now
using midpoint theorem in DABC and DACD
SR = PQ = 1/2 AC, and in DS ABD and BDC
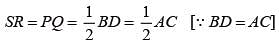
∴ SP = PQ = QR = RS
∴ PQRS is a square

∴ AP = AS = PB = BQ = QC
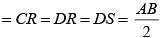
∴ In ΔAPS
AP = AS

Similarly
Similarly ∠ASP = ∠APS =∠BPQ = ∠BQP = ∠CQR
= ∠CRQ = ∠DSR = ∠DRS = 45°
Now ∠P + ∠ASP + ∠APS = 180°
⇒ ∠P = 90°
Similarly,
∠P = ∠Q = ∠R = ∠S = 90°
∴ PQRS is a parallelogram having each of its angles = 90°
Now
using midpoint theorem in DABC and DACD
SR = PQ = 1/2 AC, and in DS ABD and BDC
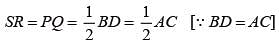
∴ SP = PQ = QR = RS
∴ PQRS is a square
Free Test
FREE
| Start Free Test |
Community Answer
The figure formed by joining the mid-points of the adjacent sides of a...
Explanation:
To understand why the figure formed by joining the mid-points of the adjacent sides of a square is a square, let's consider a square ABCD.
Definition:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
Construction:
- Let P, Q, R, and S be the midpoints of AB, BC, CD, and DA respectively.
- Join PQ, QR, RS, and SP.
Proof:
- To prove that the figure formed by joining the mid-points of the adjacent sides of a square is a square, we need to show that all four sides are equal in length and all four angles are equal to 90 degrees.
All four sides are equal in length:
- In a square ABCD, all four sides are equal. Therefore, AB = BC = CD = DA.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we have PQ || AB, QR || BC, RS || CD, and SP || DA.
- By the midpoint theorem, we know that PQ = QR = RS = SP.
- Therefore, all four sides of the figure formed by joining the mid-points are equal in length.
All four angles are equal to 90 degrees:
- In a square ABCD, all four angles are equal to 90 degrees.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we can see that PQ is parallel to AB and QR is parallel to BC.
- Since AB and BC are perpendicular to each other, PQ and QR are also perpendicular to each other.
- Similarly, RS is perpendicular to CD and SP is perpendicular to DA.
- Therefore, all four angles of the figure formed by joining the mid-points are equal to 90 degrees.
Conclusion:
- Since all four sides of the figure formed by joining the mid-points of the adjacent sides of a square are equal in length and all four angles are equal to 90 degrees, the figure is a square.
- Hence, option 'D', square, is the correct answer.
To understand why the figure formed by joining the mid-points of the adjacent sides of a square is a square, let's consider a square ABCD.
Definition:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
Construction:
- Let P, Q, R, and S be the midpoints of AB, BC, CD, and DA respectively.
- Join PQ, QR, RS, and SP.
Proof:
- To prove that the figure formed by joining the mid-points of the adjacent sides of a square is a square, we need to show that all four sides are equal in length and all four angles are equal to 90 degrees.
All four sides are equal in length:
- In a square ABCD, all four sides are equal. Therefore, AB = BC = CD = DA.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we have PQ || AB, QR || BC, RS || CD, and SP || DA.
- By the midpoint theorem, we know that PQ = QR = RS = SP.
- Therefore, all four sides of the figure formed by joining the mid-points are equal in length.
All four angles are equal to 90 degrees:
- In a square ABCD, all four angles are equal to 90 degrees.
- In the figure formed by joining the mid-points of the adjacent sides of the square, we can see that PQ is parallel to AB and QR is parallel to BC.
- Since AB and BC are perpendicular to each other, PQ and QR are also perpendicular to each other.
- Similarly, RS is perpendicular to CD and SP is perpendicular to DA.
- Therefore, all four angles of the figure formed by joining the mid-points are equal to 90 degrees.
Conclusion:
- Since all four sides of the figure formed by joining the mid-points of the adjacent sides of a square are equal in length and all four angles are equal to 90 degrees, the figure is a square.
- Hence, option 'D', square, is the correct answer.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer?
Question Description
The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer?.
The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The figure formed by joining the mid-points of the adjacent sides of a square isa)Parallelogramb)Rectanglec)Rhombusd)SquareCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Test: The Fundamental Unit of Life- Case Based Type Questions- 1
Test | 10 questions
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























