All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Circles for Class 9 Exam
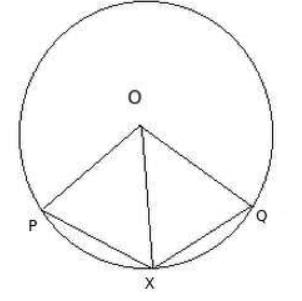
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is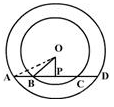
- a)20 cm
- b)50 cm
- c)60 cm
- d)43 cm
Correct answer is option 'C'. Can you explain this answer?
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is
a)
20 cm
b)
50 cm
c)
60 cm
d)
43 cm
|
|
Sarthak Satav answered |
Here OPA is right angle triangle
given OP = 16 cm
AO = 34 cm
AP = ?
using Pythagoras theorem :
AO² = OP² + AP²
34² = 16² + AP²
1156 = 256 + AP²
1156 - 256 = AP²
900 = AP²
*√900 = AP*
30 = AP
Since AD is a straight line and O is at center of both circles
AD = AP + PD
AD = AP + AP
AD = 2AP
AD = 2 x 30
*AD = 60 CM*
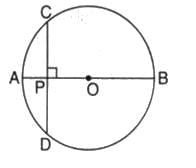
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is
- a)16 cm
- b)20 cm
- c)10 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is

a)
16 cm
b)
20 cm
c)
10 cm
d)
8 cm

|
EduRev Class 9 answered |
AP+PB=AB [diameter of circle]
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
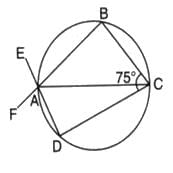
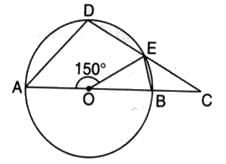
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is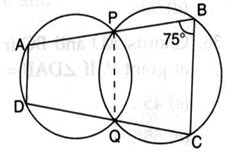
- a)75o
- b)125o
- c)105o
- d)150o
Correct answer is option 'C'. Can you explain this answer?
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is
a)
75o
b)
125o
c)
105o
d)
150o
|
|
Zachary Foster answered |
In the given figure, the points A, B, C, and D form a cyclic quadrilateral because they lie on the circumferences of the two intersecting circles.
The opposite angles of a cyclic quadrilateral are supplementary, i.e.,
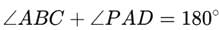
It is given that ∠ABC=75∘
Using the property of cyclic quadrilaterals:
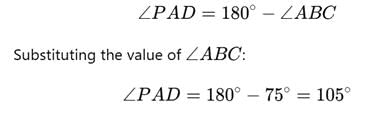
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'B'. Can you explain this answer?
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Zachary Foster answered |
Let AB be the chord of the circle with center O
.

Given that AB = Radius of the circle.
Also, AO = BO = Radius
∴ ΔOAB is an equilateral triangle.
Thus, ∠AOB = ∠OBA = ∠OAB = 60°
Also, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = 1/2 (∠AOB)
⇒ ∠ACB = 1/2 (60°) = 30°
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115o, then the measure of ∠CAE is 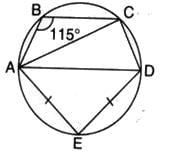
- a)70o
- b)90o
- c)80o
- d)60o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115o, then the measure of ∠CAE is

a)
70o
b)
90o
c)
80o
d)
60o

|
Nclex Coaching Centre answered |
Since AD is the diameter, the angle subtended by the diameter at any point on the circle is always 90∘. Therefore:
∠ACD = 90∘
Given AE = DE, triangle ADE is isosceles. Therefore:
∠DAE =∠DEA
Since ABCD is a cyclic quadrilateral, opposite angles of a cyclic quadrilateral sum to 180∘:
∠ABC + ∠ADC = 180∘
Substituting ∠ABC=115∘
∠ADC =180∘−115∘= 65∘
In triangle ADE, since AE = DE, we have:
∠DAE=∠DEA
As ∠ADC=65∘(external angle of triangle ADE), we know that:
∠DAE = 1 / 2 × 65∘= 32.5∘
Finding ∠CAE: Since ∠CAE=∠DAE, we find:
∠CAE = 70∘
Chords AB and CD intersect at right angles. If ∠BAC = 40o, then ∠ABD is equal to
- a)45o
- b)50o
- c)60o
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Chords AB and CD intersect at right angles. If ∠BAC = 40o, then ∠ABD is equal to
a)
45o
b)
50o
c)
60o
d)
none of these
|
|
Zachary Foster answered |
The correct answer is 50°
GIVEN: Chords AB and CD intersect at right angle. ∠BAC = 40°
TO FIND: ∠ABD
SOLUTION
We can simply solve the above problem as follows;
Let the point of intersection of the chord be 'O'.
∠AOC = 90°
Therefore,
In ΔAOC
∠AOC + ∠OAC + ∠ACO = 180°
90 + 40 + ∠ACO = 180
∠ACO = 180- 130 = 50°
Now,
AO :CO = 5:4 [since larger angle denotes shorter length]
Therefore,
Ratio of-
OB:OD=4:5 [ since they intersect and ratio gets changed]
or,
∠OBD:∠ODB=5:4 [larger length has smaller ratio]
Therefore,
∠OBD+∠ODB+90=180
5x + 4x + 90 = 180
9x + 90 = 180
x + 10 = 20
x = 10
∠OBD = 5 × 10 = 50°
Since,
∠OBD = ∠ABD
Therefore,
∠ABD = 50°
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to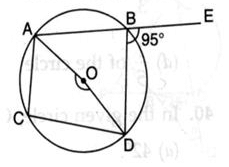
- a)190o
- b)170o
- c)180o
- d)175o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to
a)
190o
b)
170o
c)
180o
d)
175o
|
|
Zachary Foster answered |
AE is a straight line so,
angle ABD + angle EBD = 180°
angle ABD + 95° = 180°
angle ABD = 180° - 95°
angle ABD = 85°
so, it is interior angle of circle
So, angle AOD is double of angle suspended on the circle
angle AOD = 2ABD
angle AOD = 2(85°)
angle AOD = 170°
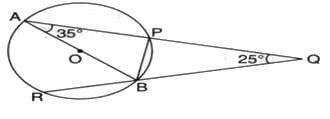
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is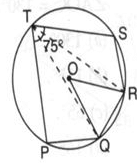
- a)25o
- b)20o
- c)50o
- d)75o
Correct answer is option 'C'. Can you explain this answer?
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is
a)
25o
b)
20o
c)
50o
d)
75o

|
Kyojuro Rengoku answered |
PQ=QR=RS
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to
- a)120o
- b)100o
- c)80o
- d)75o
Correct answer is option 'C'. Can you explain this answer?
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to
a)
120o
b)
100o
c)
80o
d)
75o

|
Let's Tute answered |
Given, ABCD is a parallelogram and AEFD is a cyclic quadrilateral.
∠BEF=80∘
Now, ∠ADC=∠BEF=80∘ (Angle of a cyclic quadrilateral is equal to the opposite exterior angle )
Also, now in parallelogram ABCD,
∠ABC=∠ADC=80∘ (Opposite angles of a parallelogram are equal)
∠BEF=80∘
Now, ∠ADC=∠BEF=80∘ (Angle of a cyclic quadrilateral is equal to the opposite exterior angle )
Also, now in parallelogram ABCD,
∠ABC=∠ADC=80∘ (Opposite angles of a parallelogram are equal)
The region between chord and either of the arc is called- a)a sector
- b)a semicircle
- c)a segment
- d)a quarter circle
Correct answer is option 'C'. Can you explain this answer?
The region between chord and either of the arc is called
a)
a sector
b)
a semicircle
c)
a segment
d)
a quarter circle

|
Nclex Coaching Centre answered |
The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle. The segment formed by minor arc along with chord, is called minor segment and the segment formed by major arc, is called the major segment.
In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to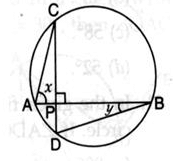
- a)75o
- b)90o
- c)45o
- d)60o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to
a)
75o
b)
90o
c)
45o
d)
60o
|
|
Zachary Foster answered |
In the circle, AB and CD are two chords which intersect each other at P at right angle i.e. ∠CPB=90o.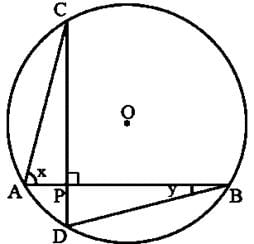

∠CAB and ∠CDB are in the same segment.
∴ ∠CDB=∠CAB=x
Now, in ΔPDB, Ext. ∠CPB=∠D+∠DBP
⇒90o = x+y (∵CD⊥AB)
Hence, x+y = 90o
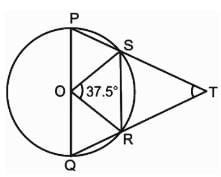
In the given figure ∠SOR = 37.5° find the value of ∠PTQ.
- a)60°
- b)67°
- c)45°
- d) 71.25°
Correct answer is option 'D'. Can you explain this answer?
In the given figure ∠SOR = 37.5° find the value of ∠PTQ.


a)
60°
b)
67°
c)
45°
d)
71.25°

|
EduRev Class 9 answered |
∠SOR = 37.5°
∠SQT = 1/2 ∠SOR (Angle at the circumference is half of the angle at the centre)
⇒ 37.5°/2
⇒ 18.75°
∠QSP = 90° (angle made from the diameter to the circumference is 90°)
Now,
∠PSQ + ∠QST = 180° (Linear pair angle)
∠QST = 180° - 90° = 90°
In ∆QST,
∠STQ = 180° - (90° + 18.75°)
⇒ ∠STQ = 71.25°
BC is a diameter of the circle and ∠BAO = 60o . Then ∠ADC is equal to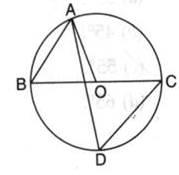
- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'C'. Can you explain this answer?
BC is a diameter of the circle and ∠BAO = 60o . Then ∠ADC is equal to
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Swati Malkani answered |
Option C is correct i.e 60 degree
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75o, ∠ABD = 58o and ∠ADC = 77o , AC and BD intersect at P. the measure of ∠DPC is

- a)92o
- b)105o
- c)90o
- d)94o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75o, ∠ABD = 58o and ∠ADC = 77o , AC and BD intersect at P. the measure of ∠DPC is

a)
92o
b)
105o
c)
90o
d)
94o

|
Varsha Pawar answered |
ANS:- let ∠PBC = x
∠ADC + ∠ABC = 180... ( opposite angles of a cyclic quadrilateral are supplementary)
77+ ∠ABD + x =180.. (∠ABC =∠ABD + x)
77+58+x =180.
135 + x =180
x = 180-135
x =45
∠PBC=45..(1)
Now , in ∆ADB,
∠ABD+∠BAD+ ∠ADB=180
58+75+ ∠ADB=180.
133+∠ADB=180.
∠ADB=180-133
∠ADB=47.
Here,. ∠ACB = ∠ADB... (angles in the same segment are equal)
Therefore,. ∠ACB=47....(2)
Now in ∆DPC,
∠DPC = ∠ACB + ∠PBC ..(exterior angle theoram.)
∠DPC= 47+45.... [from(1) and (2)]
Therefore,. ∠DPC=92.
∠ADC + ∠ABC = 180... ( opposite angles of a cyclic quadrilateral are supplementary)
77+ ∠ABD + x =180.. (∠ABC =∠ABD + x)
77+58+x =180.
135 + x =180
x = 180-135
x =45
∠PBC=45..(1)
Now , in ∆ADB,
∠ABD+∠BAD+ ∠ADB=180
58+75+ ∠ADB=180.
133+∠ADB=180.
∠ADB=180-133
∠ADB=47.
Here,. ∠ACB = ∠ADB... (angles in the same segment are equal)
Therefore,. ∠ACB=47....(2)
Now in ∆DPC,
∠DPC = ∠ACB + ∠PBC ..(exterior angle theoram.)
∠DPC= 47+45.... [from(1) and (2)]
Therefore,. ∠DPC=92.
In the given figure if ∠CAB = 49o and ∠ADC = 43o, then the measure of ∠ACB is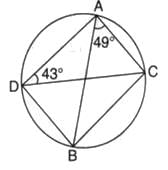
- a)92o
- b)88o
- c)74o
- d)96o
Correct answer is option 'B'. Can you explain this answer?
In the given figure if ∠CAB = 49o and ∠ADC = 43o, then the measure of ∠ACB is

a)
92o
b)
88o
c)
74o
d)
96o
|
|
Zachary Foster answered |
Angle ADC = Angle CBA(: AC is the same point that makes the angle ADC and angle CBA.)
43° = Angle CBA
In triangle ACB
Angle BAC + Angle ACB + Angle ABC = 180°
49° + Angle ACB +43° = 180°
180° - 92° = ∠ACB
88° = Angle ACB
43° = Angle CBA
In triangle ACB
Angle BAC + Angle ACB + Angle ABC = 180°
49° + Angle ACB +43° = 180°
180° - 92° = ∠ACB
88° = Angle ACB
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40o and 30o respectively. Then, the measure of ∠AOC is 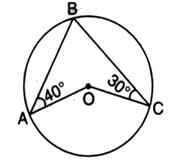
- a)170o
- b)120o
- c)110o
- d)140o
Correct answer is option 'D'. Can you explain this answer?
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40o and 30o respectively. Then, the measure of ∠AOC is

a)
170o
b)
120o
c)
110o
d)
140o
|
|
C K Academy answered |
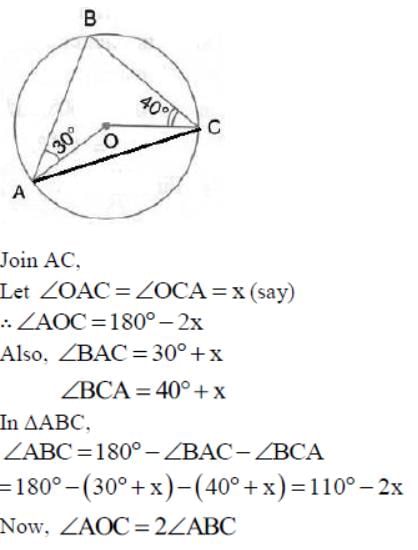
(Angle at the centre is double the angle at the circumference subtended by the same chord)
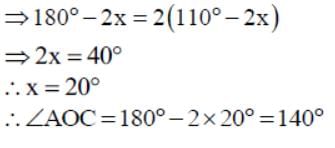
Two equal chords AB and CD of a circle are such that the length of perpendicular OE on CD = 5 cm. If OF is the perpendicular on AB, then OF =- a)5 cm
- b)2.5 cm
- c)10 cm
- d)15 cm
Correct answer is option 'A'. Can you explain this answer?
Two equal chords AB and CD of a circle are such that the length of perpendicular OE on CD = 5 cm. If OF is the perpendicular on AB, then OF =
a)
5 cm
b)
2.5 cm
c)
10 cm
d)
15 cm
|
|
Rudra Shandilya answered |
Equal chords are equidistant from the centre, so length of OF=OE=5 cm
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. The length of the common chord is- a)5 cm
- b)8 cm
- c)6 cm
- d)10 cm
Correct answer is option 'C'. Can you explain this answer?
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. The length of the common chord is
a)
5 cm
b)
8 cm
c)
6 cm
d)
10 cm
|
|
Zachary Foster answered |
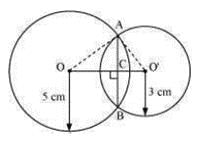
Let the radius of the circle centered at O and O' be 5 cm and 3 cm respectively.
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
∴ AC = CB
⇒ 52 = AC2 + x2
⇒ 25 − x2 = AC2 ...(1)
In ΔO'AC,
O'A2 = AC2 + O'C2
⇒ 32 = AC2 + (4 − x)2
⇒ 9 = AC2 + 16 + x2 − 8x
⇒ AC2 = − x2 − 7 + 8x ... (2)
From equations (1) and (2), we obtain
25 − x2 = − x2 − 7 + 8x
8x = 32
x = 4
Therefore, the common chord will pass through the centre of the smaller circle i.e., O' and hence, it will be the diameter of the smaller circle.
AC2 = 25 − x2 = 25 − 42 = 25 − 16 = 9
∴ AC = 3 m
Length of the common chord AB = 2 AC = (2 × 3) m = 6 m
The perpendicular distance of a chord 8 cm long from the centre of a circle of radius 5 cm is- a)2 cm
- b)9 cm
- c)4 cm
- d)3 cm
Correct answer is option 'D'. Can you explain this answer?
The perpendicular distance of a chord 8 cm long from the centre of a circle of radius 5 cm is
a)
2 cm
b)
9 cm
c)
4 cm
d)
3 cm

|
Nclex Coaching Centre answered |
Consider a circle having center O with a chord. Let OA be the radius of the circle and AB be the chord. As given in the question, the radius of the circle is 5 cm and length of chord is 8 cm. Let the distance between the center of the circle and chord be OP. So, this can be shown diagrammatically as:
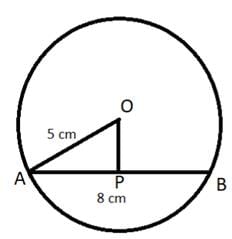
It is clear from the diagram that OP is perpendicular to AB. As OP is perpendicular to AB and passes through the center O, it will bisect the chord AB at P. Now the length of AP will be,
AP =1/2 × AB
AP =1/2 × AB
AP = 1/2 × 8
AP = 4 cm
Since, triangle OPA is a right-angle triangle, we can easily apply the Pythagoras theorem which can be stated as b2+p2 = h2 where b, p and h are base, perpendicular and hypotenuse of the respective triangle.
In ΔOPA,
Since, triangle OPA is a right-angle triangle, we can easily apply the Pythagoras theorem which can be stated as b2+p2 = h2 where b, p and h are base, perpendicular and hypotenuse of the respective triangle.
In ΔOPA,
AP2+OP2=AO2
OP2 = AO2 − AP2
OP2= 52−42
OP = 3 cm
Therefore, the distance of the chord AB from the center is 3 cm.
Therefore, the distance of the chord AB from the center is 3 cm.
Angle formed in minor segment of a circle is- a)a straight angle
- b)an acute angle
- c)a right angle
- d)an obtuse angle
Correct answer is option 'D'. Can you explain this answer?
Angle formed in minor segment of a circle is
a)
a straight angle
b)
an acute angle
c)
a right angle
d)
an obtuse angle
|
|
Zachary Foster answered |
Whenever a chord is drawn in a circle two segments are formed. One is called the minor segment while the other is called the major segment.
The angle formed by the chord in the minor segment will always be obtuse.
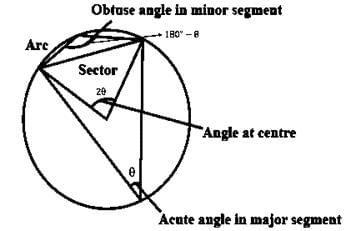
The angle formed by the chord in the minor segment will always be obtuse.

In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to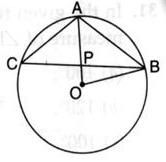
- a)72o
- b)98o
- c)90o
- d)96o
Correct answer is option 'D'. Can you explain this answer?
In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to
a)
72o
b)
98o
c)
90o
d)
96o

|
Nclex Coaching Centre answered |
For a regular n-sided polygon inscribed in a circle, the central angle subtended by each side is:
Central Angle = 360∘ / n
For the pentagon (n=5), the central angle subtended by AB is:
360∘ / 5 =72∘
For the hexagon (n=6), the central angle subtended by AC is:
360∘ / 6 = 60∘
The angle ∠APB between the two intersecting chords AB and AC can be calculated using the property of angles formed by intersecting chords: ∠APB = 1 /2 × (Sum of the arcs subtended by the opposite segments)
- Arc subtended by AB: 72∘
- Arc subtended by AC: 60∘
- The sum of the opposite arcs involved is: 72∘+120∘=192∘
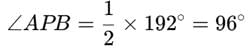
In the given figure, if ∠AOB = 80o and ∠ABC = 30o , then ∠CAO is equal to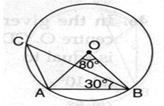
- a)30o
- b)60o
- c)80o
- d)40o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, if ∠AOB = 80o and ∠ABC = 30o , then ∠CAO is equal to
a)
30o
b)
60o
c)
80o
d)
40o

|
Namita Ranjan answered |
2ACB=AOB
ACB=40
CAB+ACB+ABC=180
CAB=180-70
CAB=110
since,OA=OB(radius)
OAB=OBA
AOB+OAB+OBA=180
2OBA=100
OBA=50
CAO=CAB-OBA=110-5O
CAO=60
ACB=40
CAB+ACB+ABC=180
CAB=180-70
CAB=110
since,OA=OB(radius)
OAB=OBA
AOB+OAB+OBA=180
2OBA=100
OBA=50
CAO=CAB-OBA=110-5O
CAO=60
In the given figure, a circle is centred at O. The value of x is :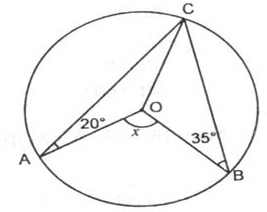
- a)55o
- b)70o
- c)110o
- d)125o
Correct answer is option 'C'. Can you explain this answer?
In the given figure, a circle is centred at O. The value of x is :
a)
55o
b)
70o
c)
110o
d)
125o

|
Nclex Coaching Centre answered |
Use the Property for Angles Subtended at the Center: The total angle subtended by the arc AB at the center O is given by:
∠AOB = 2 × ∠CAB + 2 × ∠CBA
Substitute the Given Values:
∠AOB = 2 × 20∘ + 2 × 35∘
Simplify: ∠AOB = 40∘+ 70∘= 110∘
In the given figure, the measure of angle BCD is
- a)100°
- b)75°
- c)60°
- d)50°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, the measure of angle BCD is
a)
100°
b)
75°
c)
60°
d)
50°

|
Nclex Coaching Centre answered |
The angle subtended by an arc at the center of the circle is twice the angle subtended by the same arc at any point on the circumference.
- ∠ABC=70∘, subtended by the arc AC.
- Therefore, the angle subtended by the same arc AC at the circumference on the opposite side (∠BCD) can be calculated.
∠BCD = 180∘ − (∠BAD + ∠ABC)
∠BCD = 180∘ − (50∘+70∘)
∠BCD = 60∘
In the given circle, O is the centre and ∠BDC = 42o. Then, ∠ACB is equal to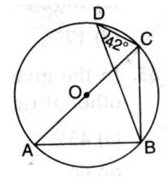
- a)58o
- b)42o
- c)52o
- d)48o
Correct answer is option 'D'. Can you explain this answer?
In the given circle, O is the centre and ∠BDC = 42o. Then, ∠ACB is equal to
a)
58o
b)
42o
c)
52o
d)
48o
|
|
Pooja Shah answered |
In ∆ BDC and ∆ BAC
Angle BAC = BDC
(angle made on same segment BC)
Since ABC is making right angle (90)
So,
In ∆ABC
ABC +BAC+ACB=180
(angle sum property of triangle)
90+42+ACB=180
ACB=180-132
ACB=48o
Angle BAC = BDC
(angle made on same segment BC)
Since ABC is making right angle (90)
So,
In ∆ABC
ABC +BAC+ACB=180
(angle sum property of triangle)
90+42+ACB=180
ACB=180-132
ACB=48o
The radius of a circle which has a 6 cm long chord, 4 cm away from the centre of the circle is- a)9 cm
- b)8 cm
- c)10 cm
- d)5 cm
Correct answer is option 'D'. Can you explain this answer?
The radius of a circle which has a 6 cm long chord, 4 cm away from the centre of the circle is
a)
9 cm
b)
8 cm
c)
10 cm
d)
5 cm
|
|
Zachary Foster answered |

In the right triangle OAP,
OA2 = OP2 +AP2 (By Pythagoras theorem)
OA2 = 42 + 32 (perpendicular from the centre of the circle bisects the chord , AP=3cm)
OA2 = 25
OA = 5
Hence the radius of the circle is 5 cm.
The length of chord which is at a distance of 12 cm from centre of circle of radius 13 cm is:- a)12 cm
- b)13 cm
- c)5 cm
- d)10 cm
Correct answer is option 'D'. Can you explain this answer?
The length of chord which is at a distance of 12 cm from centre of circle of radius 13 cm is:
a)
12 cm
b)
13 cm
c)
5 cm
d)
10 cm
|
|
Rajput Sanjanajamwal San answered |
The drawn right triangle;
Hypotenuse H= Radius of circle =13 cm.
P= perpendicular distance =12 cm, and
′L′ be the length of half-chord
(Note that By the property of Circle, Perpendicular drawn from Centre to Chord Bisects the Chord.)
By Pythagoras theorem, in the drawn right triangle shown in figure,
H2=L2+P2
L=132–122=5 cm
Now, length of the chord is 2.L=10cm
Therefore the length of chord will be 10 cm.
So, option D will be the answer.
Hypotenuse H= Radius of circle =13 cm.
P= perpendicular distance =12 cm, and
′L′ be the length of half-chord
(Note that By the property of Circle, Perpendicular drawn from Centre to Chord Bisects the Chord.)
By Pythagoras theorem, in the drawn right triangle shown in figure,
H2=L2+P2
L=132–122=5 cm
Now, length of the chord is 2.L=10cm
Therefore the length of chord will be 10 cm.
So, option D will be the answer.
Number of circles that can be drawn through three non-collinear points is- a)3
- b)1
- c)2
- d)0
Correct answer is option 'B'. Can you explain this answer?
Number of circles that can be drawn through three non-collinear points is
a)
3
b)
1
c)
2
d)
0
|
|
Aravind Menon answered |
Explanation:
To understand the number of circles that can be drawn through three non-collinear points, let's consider the given points as A, B, and C.
Definition:
A circle can be uniquely defined by three non-collinear points.
Proof:
To prove that only one circle can be drawn through three non-collinear points, we need to show that the center and radius of the circle can be uniquely determined.
Construction:
Let's construct a circle by taking two arbitrary points A and B as the endpoints of the diameter. The center of the circle will lie on the perpendicular bisector of AB.
Case 1:
If the third point C lies on the perpendicular bisector of AB, then the circle is uniquely determined. The center of the circle will be the midpoint of AB, and the radius will be half the distance between A and B.
Case 2:
If the third point C does not lie on the perpendicular bisector of AB, then the circle is not uniquely determined. Two possible circles can be drawn through the three non-collinear points.
Proof of Case 2:
To prove that two circles can be drawn through three non-collinear points, let's consider the following scenario. Assume that the points A, B, and C are not collinear, and the circle with center O and radius r is uniquely determined.
Construction:
Let's construct a line passing through C and perpendicular to AB. This line intersects the perpendicular bisector of AB at a point D.
Case 2.1:
If C lies on the same side of AB as D, then the circle with center O and radius r can be drawn.
Case 2.2:
If C lies on the opposite side of AB as D, then another circle with center O' and radius r can be drawn. The center O' will be the reflection of O with respect to AB.
Therefore, in this case, two circles can be drawn through three non-collinear points.
Conclusion:
In conclusion, the correct answer is option B) 1. Only one circle can be drawn through three non-collinear points.
To understand the number of circles that can be drawn through three non-collinear points, let's consider the given points as A, B, and C.
Definition:
A circle can be uniquely defined by three non-collinear points.
Proof:
To prove that only one circle can be drawn through three non-collinear points, we need to show that the center and radius of the circle can be uniquely determined.
Construction:
Let's construct a circle by taking two arbitrary points A and B as the endpoints of the diameter. The center of the circle will lie on the perpendicular bisector of AB.
Case 1:
If the third point C lies on the perpendicular bisector of AB, then the circle is uniquely determined. The center of the circle will be the midpoint of AB, and the radius will be half the distance between A and B.
Case 2:
If the third point C does not lie on the perpendicular bisector of AB, then the circle is not uniquely determined. Two possible circles can be drawn through the three non-collinear points.
Proof of Case 2:
To prove that two circles can be drawn through three non-collinear points, let's consider the following scenario. Assume that the points A, B, and C are not collinear, and the circle with center O and radius r is uniquely determined.
Construction:
Let's construct a line passing through C and perpendicular to AB. This line intersects the perpendicular bisector of AB at a point D.
Case 2.1:
If C lies on the same side of AB as D, then the circle with center O and radius r can be drawn.
Case 2.2:
If C lies on the opposite side of AB as D, then another circle with center O' and radius r can be drawn. The center O' will be the reflection of O with respect to AB.
Therefore, in this case, two circles can be drawn through three non-collinear points.
Conclusion:
In conclusion, the correct answer is option B) 1. Only one circle can be drawn through three non-collinear points.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer asAssertion : The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.Reason : Two or more circles are called concentric circles if and only if they have different centre and radii.- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
- d)Assertion is false but reason is true
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
Reason : Two or more circles are called concentric circles if and only if they have different centre and radii.
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
d)
Assertion is false but reason is true
|
|
Meera Rana answered |
Two or more circles are called concentric circles if and only if they have same centre but different radii.
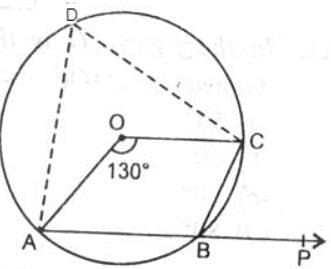
In the given figure, O is the centre of the circle and ∠AOC = 130o. Then ∠ABC is equal to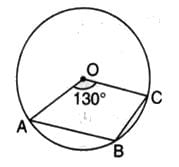
- a)115o
- b)130o
- c)65o
- d)165o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, O is the centre of the circle and ∠AOC = 130o. Then ∠ABC is equal to

a)
115o
b)
130o
c)
65o
d)
165o
|
|
Astha Shukla answered |
Here is the answer
360 degree - 130 degree =230 degree
Therefore, angle ABC =1/2reflex angle AOC
Angle ABC =1/2 230 degree
So, angle ABC =115 degree
Hope it helps you
360 degree - 130 degree =230 degree
Therefore, angle ABC =1/2reflex angle AOC
Angle ABC =1/2 230 degree
So, angle ABC =115 degree
Hope it helps you
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer asAssertion : A diameter of a circle is the longest chord of the circle and all diameters have equal length.Reason : Length of a diameter = radius.- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
Correct answer is option ''. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : A diameter of a circle is the longest chord of the circle and all diameters have equal length.
Reason : Length of a diameter = radius.
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
|
|
Swati Verma answered |
Length of diameter = 2 × radius.
So, Reason is false.
Also, chord is a line connecting two points on a circle. The farthest points are the ones which are collinear to the centre of the circle. Points collinear to the centre of the circle are joined by the diameter. Hence diameter is the longest chord. Assertion is correct but Reason is false.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer asAssertion : The circumference of a circle must be a positive real number.Reason : If r(>) 0 is the radius of the circle, then its circumference 2πr is a positive real number.- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
- d)Assertion is false but reason is true
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The circumference of a circle must be a positive real number.
Reason : If r(>) 0 is the radius of the circle, then its circumference 2πr is a positive real number.
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
d)
Assertion is false but reason is true
|
|
Aditi Sharma answered |
The circumference of a circle is its perimeter or distance around it. It is denoted by C in math formulas and has units of distance, such as millimeters (mm), centimeters (cm), meters (m), or inches (in). It is related to the radius, diameter, and pi using the following equations: C = πd. C = 2πr.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The measure of ∠AOC = 60º Reason : Angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by arc on the circumference.
Reason : Angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by arc on the circumference.
- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
- d)Assertion is false but reason is true.
Correct answer is option 'D'. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The measure of ∠AOC = 60º

Reason : Angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by arc on the circumference.
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
d)
Assertion is false but reason is true.
|
|
Meera Rana answered |
Join BO.
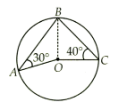
In ΔAOB , we have
OA = OB [radius]
∠OBA = ∠OAB
[Angle opposite to equal sides of a triangle are equal]
∠OBA = 30º ...(1)
Similarly, in ΔBOC , we get OB = OC
∠OCB = ∠OBC
∠OBC = 40º ...(2)
∠ABC = ∠OBA + ∠OBC
= 30º + 40º = 70º
[Using (1) and (2)]
Since angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by the arc on the circumference.
∠AOC = 2 x ∠ABC
= 2 x 70º = 140º
As the Assertion states that ∠AOC=60∘, it is false.
As the Assertion states that ∠AOC=60∘, it is false.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer asAssertion : The length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm is 17.32 cm.Reason : The perpendicular from the centre of a circle to a chord bisects the chord.- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
- d)Assertion is false but reason is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm is 17.32 cm.
Reason : The perpendicular from the centre of a circle to a chord bisects the chord.
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
d)
Assertion is false but reason is true.
|
|
Aditi Sharma answered |
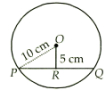
Let, PQ be a chord of a circle with centre O and radius 10cm. Draw OR ⊥PQ = .
Now, OP = 10cm and OR = 5cm
In right triangle ORP, we get
OP2 = PR2 + OR2
PR2 = OP2 - OR2
PR2 = 102 - 52 = 75
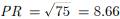
Since, the perpendicular from the centre to a chord bisects the chord.
Therefore, PQ = 2 x PR
= 2 x 8.66 = 17.32 cm
What fraction of the whole circle is minor arc RP in the given figure ?
- a)1/5 of the circle
- b)1/2 of the circle
- c)1/4 of the circle
- d)1/3 of the circle
Correct answer is option 'D'. Can you explain this answer?
What fraction of the whole circle is minor arc RP in the given figure ?
a)
1/5 of the circle
b)
1/2 of the circle
c)
1/4 of the circle
d)
1/3 of the circle
|
|
Zachary Foster answered |
- The central angle subtended by the minor arc RP is:Minor arc RP =∠POQ =120∘
- The fraction of the circle represented by the minor arc RP is:Fraction=Central Angle / Total Angle of the CircleSubstituting the values:Fraction = 120∘ / 360∘= 1 / 3
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer asAssertion : In an isosceles triangles ABC with AB = AC , a circle is passing through B and C intersects the sides AB and AC at D and E respectively. Then DE || BCReason : Exterior angle of a cyclic quadrilateral is equal to interior opposite angle of that quadrilateral- a)Both assertion and reason are true and reason is the correct explanation of assertion.
- b)Both assertion and reason are true but reason is not the correct explanation of assertion.
- c)Assertion is true but reason is false.
- d)Assertion is false but reason is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : In an isosceles triangles ABC with AB = AC , a circle is passing through B and C intersects the sides AB and AC at D and E respectively. Then DE || BC
Reason : Exterior angle of a cyclic quadrilateral is equal to interior opposite angle of that quadrilateral
a)
Both assertion and reason are true and reason is the correct explanation of assertion.
b)
Both assertion and reason are true but reason is not the correct explanation of assertion.
c)
Assertion is true but reason is false.
d)
Assertion is false but reason is true.
|
|
Aditya Shah answered |
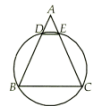
To prove DE || BC
i.e., ∠B ∠ADE .
In Δ ABC , we have
AB = AC
∠B = ∠C ...(1)
In the cyclic quadrilateral CBDE , side BD is produced to A. We know that an exterior angle of cyclic quadrilateral is equal to interior opposite angle of cyclic quadrilateral.
∠ADE = ∠C ...(2)
From (1) and (2), we get
∠B = ∠ADE .
Hence, DE || BC
A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90° and 110° respectively. Then the measure of angle BAC is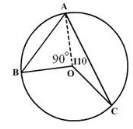
- a)40°
- b)80°
- c)75°
- d)50°
Correct answer is option 'B'. Can you explain this answer?
A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90° and 110° respectively. Then the measure of angle BAC is
a)
40°
b)
80°
c)
75°
d)
50°
|
|
Zachary Foster answered |
Given: ∠BOA=90∘ and ∠AOC=110∘
We know that angles around a point add up to 360∘
∴∠BOC+∠BOA+∠AOC=360∘
⇒∠BOC+90∘+110∘=360∘
⇒∠BOC=360∘−200∘
∠BOC=160∘
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
Arc BC is subtending ∠BOC at the center and ∠BAC on the remaining part of the circle, so ∠BOC=2×∠BAC
Chapter doubts & questions for Circles - Mathematics (Maths) Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circles - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|471 docs|57 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily