All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Heron's Formula for Class 9 Exam
The area of a triangle with base 8 cm and height 10 cm is
- a)20 cm2
- b)18 cm2
- c)80 cm2
- d)40 cm2
Correct answer is option 'D'. Can you explain this answer?
The area of a triangle with base 8 cm and height 10 cm is
a)
20 cm2
b)
18 cm2
c)
80 cm2
d)
40 cm2
|
|
Samaira Kapoor answered |
Given:
Base of the triangle = 8 cm
Height of the triangle = 10 cm
To find:
Area of the triangle
Formula:
Area of the triangle = 1/2 × base × height
Solution:
Substituting the given values in the formula, we get
Area of the triangle = 1/2 × 8 cm × 10 cm
Area of the triangle = 40 cm²
Therefore, the correct option is (d) 40 cm².
Base of the triangle = 8 cm
Height of the triangle = 10 cm
To find:
Area of the triangle
Formula:
Area of the triangle = 1/2 × base × height
Solution:
Substituting the given values in the formula, we get
Area of the triangle = 1/2 × 8 cm × 10 cm
Area of the triangle = 40 cm²
Therefore, the correct option is (d) 40 cm².
The area of quadrilateral PQRS, in which PQ = 7 cm, QR = 6 cm, RS = 12 cm, PS = 15 cm and PR = 9 cm:- a)74.98 cm2
- b)25.25 cm2
- c)75 cm2
- d)68.25 cm2
Correct answer is option 'A'. Can you explain this answer?
The area of quadrilateral PQRS, in which PQ = 7 cm, QR = 6 cm, RS = 12 cm, PS = 15 cm and PR = 9 cm:
a)
74.98 cm2
b)
25.25 cm2
c)
75 cm2
d)
68.25 cm2
|
|
Ishan Choudhury answered |
s = a + b + c /2 = 12 + 9 + 15 /2 = 18cm
Area of PRS = √s(s - a)(s - b)(s - c) = 54 cm^2
s = a + b + c /2 = 7 + 6 + 9 /2 = 11 cm
Area of RPQ = √s(s - a)(s - b)(s - c) = 20.98 cm^2
Area of Quadrilateral = Area of RPQ + Area of PRS
= 54 + 20.98
= 74.98 cm^2
The area of triangle, whose sides are 15 cm, 25 cm and 14 cm:
- a)18 √26 cm2
- b)15 √29 cm2
- c)17 √23 cm2
- d)20 √26 cm2
Correct answer is option 'A'. Can you explain this answer?
The area of triangle, whose sides are 15 cm, 25 cm and 14 cm:
a)
18 √26 cm2
b)
15 √29 cm2
c)
17 √23 cm2
d)
20 √26 cm2

|
Rohini Seth answered |
Let
a = 15cm
b = 25cm
c = 14cm
Semi-Perimeter = a + b + c / 2
= 15 + 25 + 14 / 2
= 54 / 2
= 27 cm.
Area Through Heron's Formula
= √s(s-a)(s-b)(s-c)
= √27(27-15)(27-25)(27-14)
= √27 × 12 × 2 × 13
= √3 × 3 × 3 × 2 × 2 × 3 × 13
= 3 × 3 × 2 √13
= 18 √13
a = 15cm
b = 25cm
c = 14cm
Semi-Perimeter = a + b + c / 2
= 15 + 25 + 14 / 2
= 54 / 2
= 27 cm.
Area Through Heron's Formula
= √s(s-a)(s-b)(s-c)
= √27(27-15)(27-25)(27-14)
= √27 × 12 × 2 × 13
= √3 × 3 × 3 × 2 × 2 × 3 × 13
= 3 × 3 × 2 √13
= 18 √13
The sides of a triangle are in the ratio 25 : 17 : 12 and its perimeter is 540m. The area of the triangle is- a)12000 m2
- b)5000 m2
- c)9000 m2
- d)10000 m2
Correct answer is option 'C'. Can you explain this answer?
The sides of a triangle are in the ratio 25 : 17 : 12 and its perimeter is 540m. The area of the triangle is
a)
12000 m2
b)
5000 m2
c)
9000 m2
d)
10000 m2
|
|
Arvind Singh answered |
perimeter = 540m
sides are in ratio 25:17:12
The sides are 25x , 17x , 12x where x is any positive no.
Now
25x + 17x + 12x = 540
54x = 540
x = 10
25x = 25 * 10 = 250
17x = 17*10 = 170
12x = 12*10 = 120
So, the sides are 250m , 170m & 120m.
now, the semi - perimeter is S = 540/2 = 270 m
we know the Heron's formula:-
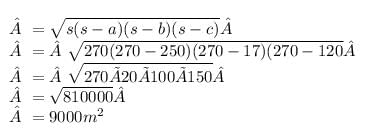
Area of triangle is 9000m^2
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
- a)32 cm2
- b)54 cm2
- c)67 cm2
- d)72cm2
Correct answer is option 'B'. Can you explain this answer?
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
a)
32 cm2
b)
54 cm2
c)
67 cm2
d)
72cm2
|
|
Krishna Iyer answered |
It is given that the sides of a triangle are in the ratio 3 : 4 : 5.
Let the length of sides are 3x, 4x and 5x.
It's perimeter is 36 cm.
3x+4x+5x = 36
12x = 36
x = 3
The value of x is 3. The length of sides are 9, 12, 15.
It is an right angled triangle because the sum of squares of two smaller sides is equal to the square of larger sides.
92 + 122 = 152
81 + 144 = 225
Here, the length of hypotenuse is 15 cm.
The area of triangle is
1/2 x 9 x12
54 cm2
The area of an equilateral triangle with perimeter 18x is:- a)9√3 sq. units
- b)9x2√3 sq. units
- c)18√3 sq. units
- d)18x2√3 sq. units
Correct answer is option 'B'. Can you explain this answer?
The area of an equilateral triangle with perimeter 18x is:
a)
9√3 sq. units
b)
9x2√3 sq. units
c)
18√3 sq. units
d)
18x2√3 sq. units
|
|
Amit Kumar answered |
let each side be a
so perimeter is 3a = 18x
a=6x
so area = √3a2/4
=√3*36x2/4
=9x2√3 sq. units
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?- a)32 cm2
- b)54 cm2
- c) 67 cm2
- d)72cm2
Correct answer is 'B'. Can you explain this answer?
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
a)
32 cm2
b)
54 cm2
c)
67 cm2
d)
72cm2
|
|
Ananya Das answered |
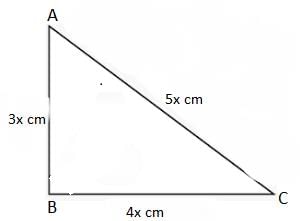
⇒ AB + BC + CA = 36 cm
⇒ 3x + 4x + 5x = 36 cm
⇒ 12x = 36
⇒ x = 3
∴ AB = 3x = 9
BC = 4x = 12
CA = 5x = 15
Now, (AB)2 + (BC)2
= (9)2 + (12)2
= 81 + 144
= 255
= (AC)2
Δ ABC is a right angle triangle and ∠B is right angle.
Area of Δ ABC = 1/2 (AB x BC)
= 1/2 (9 x12)
= 54 cm2
If each side of an equilateral triangle is increased by 2 cm, then its area increases by 3√3 cm2. The length of its each side and its area are respectively equal to
- a)3 cm, √3cm2
- b)2 cm, √3cm2
- c)2 cm, √8 cm2
- d)2 cm, √5 cm2
Correct answer is option 'B'. Can you explain this answer?
If each side of an equilateral triangle is increased by 2 cm, then its area increases by 3√3 cm2. The length of its each side and its area are respectively equal to
a)
3 cm, √3cm2
b)
2 cm, √3cm2
c)
2 cm, √8 cm2
d)
2 cm, √5 cm2

|
EduRev Class 9 answered |

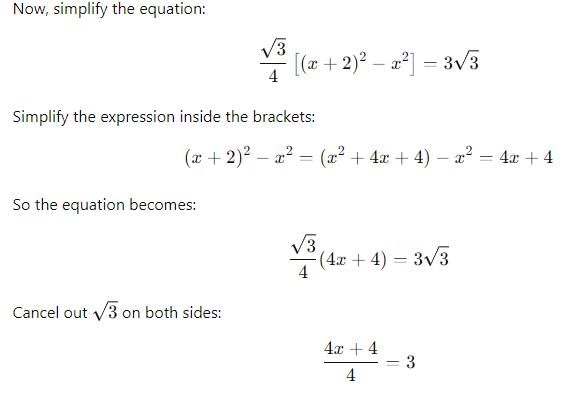

An isosceles right triangle has area 8 cm2. The length of its hypotenuse is :
- a)√16 cm
- b)√48 cm
- c)√32 cm
- d)√24 cm
Correct answer is option 'C'. Can you explain this answer?
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is :
a)
√16 cm
b)
√48 cm
c)
√32 cm
d)
√24 cm

|
Shrushti Barure answered |
Given : isosceles right angle triangle
therefore base = height
area of triangle = 8 cm ^2
to find : Hypotenuse
procedure : consider base=height=X
area of right triangle = 1/2×base× height = 8
= 1/2×X×X =8
= X^2/2 = 8
= X^2=16
=X=4
Hypotenuse^2=base^2+height ^2
H^2=4^2+4^2
H^2=16+16
H^2=32
therefore. H = 32^1/2
therefore base = height
area of triangle = 8 cm ^2
to find : Hypotenuse
procedure : consider base=height=X
area of right triangle = 1/2×base× height = 8
= 1/2×X×X =8
= X^2/2 = 8
= X^2=16
=X=4
Hypotenuse^2=base^2+height ^2
H^2=4^2+4^2
H^2=16+16
H^2=32
therefore. H = 32^1/2
The area of an isosceles right angled triangle of equal side 30 cm, is given as
- a)225√3 cm2
- b)900 cm2
- c)450 cm2
- d)900 cm2
Correct answer is option 'C'. Can you explain this answer?
The area of an isosceles right angled triangle of equal side 30 cm, is given as
a)
225√3 cm2
b)
900 cm2
c)
450 cm2
d)
900 cm2

|
Ankit Saha answered |
as it is right angle triangle so
area =1/2 x base x height
=1/2 x 30 x 30
= 450 cm2
area =1/2 x base x height
=1/2 x 30 x 30
= 450 cm2
The perimeter and area of a triangle whose sides are of lengths 3 cm, 4 cm and 5 cm respectively are
- a)12 cm, 12 cm2
- b)12 cm, 6 cm2
- c)6 cm, 12 cm2
- d)6 cm, 6 cm2
Correct answer is option 'B'. Can you explain this answer?
The perimeter and area of a triangle whose sides are of lengths 3 cm, 4 cm and 5 cm respectively are
a)
12 cm, 12 cm2
b)
12 cm, 6 cm2
c)
6 cm, 12 cm2
d)
6 cm, 6 cm2

|
Imk Pathshala answered |
The perimeter of the triangle is 12 cm and the area of the triangle is 6 cm.
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be
- a)24 cm2
- b)40 cm2
- c)80 cm2
- d)48 cm2
Correct answer is option 'A'. Can you explain this answer?
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be
a)
24 cm2
b)
40 cm2
c)
80 cm2
d)
48 cm2
|
|
Mehul Ghosh answered |
Solution:
Given,
Base of right triangle = 8 cm
Hypotenuse of right triangle = 10 cm
Let the height of the right triangle be h.
Using Pythagoras theorem, we have
(hypotenuse)2 = (base)2 + (height)2
102 = 82 + h2
100 = 64 + h2
h2 = 36
h = 6 cm
Therefore, the area of the right triangle is given by
Area = 1/2 x base x height
= 1/2 x 8 x 6
= 24 cm2
Hence, the correct option is (a) 24cm2.
Given,
Base of right triangle = 8 cm
Hypotenuse of right triangle = 10 cm
Let the height of the right triangle be h.
Using Pythagoras theorem, we have
(hypotenuse)2 = (base)2 + (height)2
102 = 82 + h2
100 = 64 + h2
h2 = 36
h = 6 cm
Therefore, the area of the right triangle is given by
Area = 1/2 x base x height
= 1/2 x 8 x 6
= 24 cm2
Hence, the correct option is (a) 24cm2.
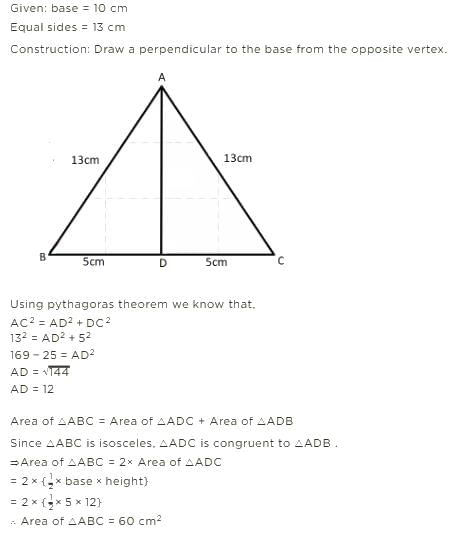
Each of the equal sides of an isosceles triangle is 2 cm greater than its height. If the base of the triangle is 12 cm, then its area is- a)40 cm2
- b)24 cm2
- c)48 cm2
- d)36 cm2
Correct answer is option 'C'. Can you explain this answer?
Each of the equal sides of an isosceles triangle is 2 cm greater than its height. If the base of the triangle is 12 cm, then its area is
a)
40 cm2
b)
24 cm2
c)
48 cm2
d)
36 cm2
|
|
Amit Sharma answered |

and, equating this with the basic area formula,
i.e. A = 1/2.h.b
Find the length of each side of an equilateral triangle having area of 9 root 3 cm square- a)36 cm
- b)5 cm
- c)15 cm
- d)6 cm
Correct answer is option 'D'. Can you explain this answer?
Find the length of each side of an equilateral triangle having area of 9 root 3 cm square
a)
36 cm
b)
5 cm
c)
15 cm
d)
6 cm
|
|
Sagnik Dasgupta answered |
Given area of equilateral triangle = 9√3 cm²
Also,
Area of the equilateral triangle = √3/4 × (side)²
So,
√3/4 × (side)² = 9√3
side² = (9√3 × 4)/√3
side² = 36
side = √36
side = 6cm
Also,
Area of the equilateral triangle = √3/4 × (side)²
So,
√3/4 × (side)² = 9√3
side² = (9√3 × 4)/√3
side² = 36
side = √36
side = 6cm
The area of an equilateral triangle of side 14 cm is- a)49√3 cm2
- b)56√3 cm2
- c)58√3 cm2
- d)18 cm2
Correct answer is option 'A'. Can you explain this answer?
The area of an equilateral triangle of side 14 cm is
a)
49√3 cm2
b)
56√3 cm2
c)
58√3 cm2
d)
18 cm2

|
Prisha Behera answered |
Side=14cm
area of equilateral triangle=(√3/4)×a^2 where a=side
using this formula,
(√3/4) × 14 ×14=49√3 cm^2
area of equilateral triangle=(√3/4)×a^2 where a=side
using this formula,
(√3/4) × 14 ×14=49√3 cm^2
In each side of a △ is halved then its perimeter will be decreased by
- a)25 %
- b)75 %
- c)50 %
- d)none
Correct answer is option 'C'. Can you explain this answer?
In each side of a △ is halved then its perimeter will be decreased by
a)
25 %
b)
75 %
c)
50 %
d)
none

|
Preeti Kumar answered |
The
perimeter of the triangle
is reduced by 50%
.Therefore, the
option (B)
is correct.Step-by-step explanation:
Consider that the sides of the triangle are a, b and c.
Perimeter
of the triangle is sum all three sided of the triangle.Perimeter of Δ 
Now, if the each side will be halved then, new perimeter P':
Percentage change in perimeter 
Here, the negative sign shows that the
new perimeter
of the triangle is reduced
by 50%.The area of a parallelogram whose base is 32 m and the corresponding altitude is 6 m isa)132 m2b)164 m2c)192m2d)None of the aboveCorrect answer is option 'C'. Can you explain this answer?
|
|
Ananya Das answered |
area of parallelogram = base x height
=32 x 6 = 192 m2
The area of an equilateral triangle of side 6 cm is- a)18 cm2
- b)9√3 cm2
- c)56√3 cm2
- d)58√3 cm2
Correct answer is option 'B'. Can you explain this answer?
The area of an equilateral triangle of side 6 cm is
a)
18 cm2
b)
9√3 cm2
c)
56√3 cm2
d)
58√3 cm2
|
|
Anshul Chatterjee answered |
The correct answer is b) 9 cm².
To find the area of an equilateral triangle, we can use the formula:
Area = (sqrt(3) / 4) * side^2
Given that the side of the equilateral triangle is 6 cm, we can substitute this value into the formula:
Area = (sqrt(3) / 4) * 6^2
= (sqrt(3) / 4) * 36
= (1.732 / 4) * 36
= 0.433 * 36
= 15.588
Therefore, the area of the equilateral triangle is approximately 15.588 cm², which rounds to 16 cm².
To find the area of an equilateral triangle, we can use the formula:
Area = (sqrt(3) / 4) * side^2
Given that the side of the equilateral triangle is 6 cm, we can substitute this value into the formula:
Area = (sqrt(3) / 4) * 6^2
= (sqrt(3) / 4) * 36
= (1.732 / 4) * 36
= 0.433 * 36
= 15.588
Therefore, the area of the equilateral triangle is approximately 15.588 cm², which rounds to 16 cm².
The perimeter of a rhombus is 20 cm. One of its diagonals is 8 cm. Then area of the rhombus is- a)24 cm2
- b)42 cm2
- c)18 cm2
- d)36 cm2
Correct answer is option 'A'. Can you explain this answer?
The perimeter of a rhombus is 20 cm. One of its diagonals is 8 cm. Then area of the rhombus is
a)
24 cm2
b)
42 cm2
c)
18 cm2
d)
36 cm2

|
Kavya Nambiar answered |
Given, Perimeter of a rhombus = 20 cm
Perimeter of a rhombus = 4*side
Hence, side = 20/4 = 5 cm.
Now, we know that the diagonals of a rhombus bisect each other at right angles (90 degree).
Hence 'a right angled triangle can be visualised with 'side' as the hypotenuse'.
diagonal length = 8 cm
Half the length (since diagonal bisects each other) = 8/2 = 4 cm
(d/2)^2 + (d1/2)^2 = 5^2
4^2 + (d1/2)^2 = 5^2
(d1/2)^2 = 9
d1/2 = 3
d1 = 3*2 = 6 cm
Hence other diagonal = 6 cm.
Area = 1/2 * d1*d = 1/2 * 8 * 6 = 24 cm^2
Hope it helps.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is- a)Rs. 2.00
- b)Rs. 2.16
- c)Rs. 2.48
- d)Rs. 3.00
Correct answer is option 'B'. Can you explain this answer?
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is
a)
Rs. 2.00
b)
Rs. 2.16
c)
Rs. 2.48
d)
Rs. 3.00
|
|
Reshma Menon answered |
To find the cost of painting the triangular board, we need to find the area of the triangle first.
**Finding the Area of the Triangle:**
We can use Heron's formula to find the area of the triangle when the lengths of its sides are known. Heron's formula states that the area of a triangle with sides a, b, and c is given by:
Area = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle and is calculated as:
s = (a + b + c) / 2
In this case, the lengths of the sides are given as 6 cm, 8 cm, and 10 cm. So, we can substitute these values into the formulas to find the area.
**Calculating the Semi-Perimeter:**
s = (6 + 8 + 10) / 2
= 24 / 2
= 12 cm
**Calculating the Area:**
Area = √(12(12-6)(12-8)(12-10))
= √(12 * 6 * 4 * 2)
= √(576)
= 24 cm²
So, the area of the triangular board is 24 cm².
**Calculating the Cost of Painting:**
The cost of painting is given as 9 paise per cm². To find the total cost, we need to multiply the area of the board by the cost per cm².
Cost = Area * Cost per cm²
= 24 cm² * 9 paise/cm²
= 216 paise
Since 1 rupee is equal to 100 paise, we can convert the cost to rupees by dividing by 100.
Cost = 216 paise / 100
= Rs. 2.16
Therefore, the cost of painting the triangular board is Rs. 2.16, which corresponds to option B.
**Finding the Area of the Triangle:**
We can use Heron's formula to find the area of the triangle when the lengths of its sides are known. Heron's formula states that the area of a triangle with sides a, b, and c is given by:
Area = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle and is calculated as:
s = (a + b + c) / 2
In this case, the lengths of the sides are given as 6 cm, 8 cm, and 10 cm. So, we can substitute these values into the formulas to find the area.
**Calculating the Semi-Perimeter:**
s = (6 + 8 + 10) / 2
= 24 / 2
= 12 cm
**Calculating the Area:**
Area = √(12(12-6)(12-8)(12-10))
= √(12 * 6 * 4 * 2)
= √(576)
= 24 cm²
So, the area of the triangular board is 24 cm².
**Calculating the Cost of Painting:**
The cost of painting is given as 9 paise per cm². To find the total cost, we need to multiply the area of the board by the cost per cm².
Cost = Area * Cost per cm²
= 24 cm² * 9 paise/cm²
= 216 paise
Since 1 rupee is equal to 100 paise, we can convert the cost to rupees by dividing by 100.
Cost = 216 paise / 100
= Rs. 2.16
Therefore, the cost of painting the triangular board is Rs. 2.16, which corresponds to option B.
Length of perpendicular drawn on longest side of a scale △ is- a)smallest
- b)largest
- c)No relation
- d)none
Correct answer is option 'A'. Can you explain this answer?
Length of perpendicular drawn on longest side of a scale △ is
a)
smallest
b)
largest
c)
No relation
d)
none
|
|
Sarita Reddy answered |
The correct answer is option 'A'.
In a triangle, the length of a perpendicular (or altitude) drawn from a vertex (corner) to the opposite side (the base) is called the "height" of the triangle. The base of the triangle can be any one of the three sides of the triangle, while the vertex from which the height is drawn is called the "apex".
When the longest side of a triangle is used as the base and a perpendicular is drawn from the opposite vertex (the apex), the resulting height is the smallest among all the possible heights that can be drawn on the triangle. This is because the longest side of the triangle will be the furthest away from the vertex, so the perpendicular will have to travel the greatest distance to reach the base, thus resulting in a shorter height.
Option A is correct as it states that the length of perpendicular drawn on longest side of a triangle is the smallest.
Option B,C,D are not correct as they do not match the statement about the length of perpendicular on the longest side of a triangle being the smallest.
In ∆ABC, angle A = 30°, side 'b' = 4 units, side 'c' = 6 units. Find the area of ∆ABC,
- a)8 cm2
- b)6 cm2
- c)5 cm2
- d)9 cm2
Correct answer is option 'B'. Can you explain this answer?
In ∆ABC, angle A = 30°, side 'b' = 4 units, side 'c' = 6 units. Find the area of ∆ABC,
a)
8 cm2
b)
6 cm2
c)
5 cm2
d)
9 cm2
|
|
Hiral Nambiar answered |
Given information:
Angle A = 30°
Side b = 4 units
Side c = 6 units
Step 1: Find side a using the Law of Cosines
Using the Law of Cosines formula:
a² = b² + c² - 2bc * cos(A)
a² = 4² + 6² - 2*4*6 * cos(30°)
a² = 16 + 36 - 48 * cos(30°)
a² = 52 - 48 * 0.866 (cos(30°) is approximately 0.866)
a² = 52 - 41.568
a² = 10.432
a ≈ √10.432
a ≈ 3.23 units
Step 2: Calculate the area of the triangle using the formula
Area of triangle ABC = 0.5 * b * c * sin(A)
Area = 0.5 * 4 * 6 * sin(30°)
Area = 0.5 * 24 * 0.5
Area = 6 cm²
Therefore, the correct answer is option b) 6 cm².
Angle A = 30°
Side b = 4 units
Side c = 6 units
Step 1: Find side a using the Law of Cosines
Using the Law of Cosines formula:
a² = b² + c² - 2bc * cos(A)
a² = 4² + 6² - 2*4*6 * cos(30°)
a² = 16 + 36 - 48 * cos(30°)
a² = 52 - 48 * 0.866 (cos(30°) is approximately 0.866)
a² = 52 - 41.568
a² = 10.432
a ≈ √10.432
a ≈ 3.23 units
Step 2: Calculate the area of the triangle using the formula
Area of triangle ABC = 0.5 * b * c * sin(A)
Area = 0.5 * 4 * 6 * sin(30°)
Area = 0.5 * 24 * 0.5
Area = 6 cm²
Therefore, the correct answer is option b) 6 cm².
The sides of a triangle are x, y and z. If x + y = 7 m, y + z = 9 m, and z + x = 8 m, then area of the triangle is :- a)6 m2
- b)5 m2
- c)7 m2
- d)4 m2
Correct answer is option 'A'. Can you explain this answer?
The sides of a triangle are x, y and z. If x + y = 7 m, y + z = 9 m, and z + x = 8 m, then area of the triangle is :
a)
6 m2
b)
5 m2
c)
7 m2
d)
4 m2
|
|
Raghav Bansal answered |
x + y = 7....(1)
y + z = 9....(2)
z + x = 8....(3)
So, 2(x+y+z) = 24
x+y+z = 12
Now, y + z = 9 then x = 3
z + x = 8 then y = 4
x + y = 7 then z = 5
We can see that, this becomes a right angled triangle.
Hence, Area of triangle = 1/2 * base * perpendicular
= 1/2 * 4 * 3
= 6 sq unit.
y + z = 9....(2)
z + x = 8....(3)
So, 2(x+y+z) = 24
x+y+z = 12
Now, y + z = 9 then x = 3
z + x = 8 then y = 4
x + y = 7 then z = 5
We can see that, this becomes a right angled triangle.
Hence, Area of triangle = 1/2 * base * perpendicular
= 1/2 * 4 * 3
= 6 sq unit.
The sides of a triangular flower bed are 5 m, 8 m and 11 m. the area of the flower bed is- a)√300 m2
- b)√330 m2
- c)21√4 m2
- d)4√21 m2
Correct answer is option 'D'. Can you explain this answer?
The sides of a triangular flower bed are 5 m, 8 m and 11 m. the area of the flower bed is
a)
√300 m2
b)
√330 m2
c)
21√4 m2
d)
4√21 m2
|
|
Saikat Iyer answered |
Using Heron's formula, we can calculate the area of the triangle:
s = (5 + 8 + 11)/2 = 12
A = √(s(s-5)(s-8)(s-11))
A = √(12(12-5)(12-8)(12-11))
A = √(12(7)(4)(1))
A = √(336)
A ≈ 18.33 m²
Therefore, the area of the flower bed is approximately 18.33 square meters.
s = (5 + 8 + 11)/2 = 12
A = √(s(s-5)(s-8)(s-11))
A = √(12(12-5)(12-8)(12-11))
A = √(12(7)(4)(1))
A = √(336)
A ≈ 18.33 m²
Therefore, the area of the flower bed is approximately 18.33 square meters.
The sides of a triangle are in the ratio of 5: 12: 13. If its perimeter is 60 cm, then what is its area?
- a)32 cm2
- b)120 cm²
- c)67 cm2
- d)72cm2
Correct answer is option 'B'. Can you explain this answer?
The sides of a triangle are in the ratio of 5: 12: 13. If its perimeter is 60 cm, then what is its area?
a)
32 cm2
b)
120 cm²
c)
67 cm2
d)
72cm2

|
Imk Pathshala answered |
Given that the sides of the triangle are in the ratio 5:12:13 and the perimeter is 60 cm, we can follow these steps:
- Find the actual side lengths: Let the common ratio factor be xxx.
So, the sides of the triangle are 5x, 12x, and 13x.The perimeter is the sum of the sides:5x+12x+13x=60
30x=60
x=2
- Therefore, the sides of the triangle are:5x=10 cm,12x=24 cm,13x=26 cm.
- Check if it's a right-angled triangle: The sides are in the ratio 5:12:13, which is a well-known Pythagorean triplet, meaning it is a right-angled triangle.
- Find the area: For a right-angled triangle, the area is:Area=12×Base×HeightHere, the base is 10 cm, and the height is 24 cm:Area=12×10×24=120 cm^2
Thus, the correct answer is:
1. 120 cm².
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be :- a)40 cm2
- b)48 cm2
- c)24 cm2
- d)80 cm2
Correct answer is option 'C'. Can you explain this answer?
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be :
a)
40 cm2
b)
48 cm2
c)
24 cm2
d)
80 cm2
|
|
Arjun Sharma answered |
Given,
base= 8cm
hypotenuse= 10cm
First, let us find the height of the triangle:
Let height = h
By applying pythagorean theorem
h 2 + 8 2 = 10 2
h 2 + 64 = 100
h 2 = 100 - 64
h 2 = 36
h = 6cm
Now let us find the area,
Area = 1/2 x b x h
= 1/2 x 8 x 6
= 1/2 x 48
= 24cm 2
Therefore, area of the right triangle = 24cm 2
There is a slide in a park. One of its side walls has been painted in some colour with a message “Keep the park green and Clean”. If sides of the wall are 15m, 11 m and 6 m, the area painted in colour is________.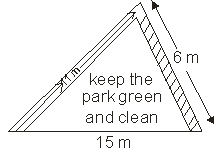
- a)20 √6 m2
- b)10 √2 m2
- c)20 √2 m2
- d)20 √3 m2
Correct answer is option 'C'. Can you explain this answer?
There is a slide in a park. One of its side walls has been painted in some colour with a message “Keep the park green and Clean”. If sides of the wall are 15m, 11 m and 6 m, the area painted in colour is________.
a)
20 √6 m2
b)
10 √2 m2
c)
20 √2 m2
d)
20 √3 m2

|
Soumya answered |
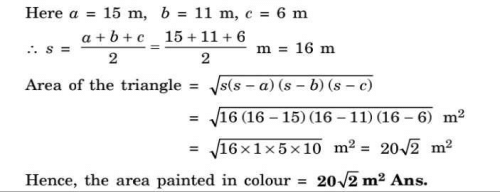
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is- a)√32 cm
- b)√16 cm
- c)√48 cm
- d)√24
Correct answer is option 'A'. Can you explain this answer?
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is
a)
√32 cm
b)
√16 cm
c)
√48 cm
d)
√24
|
|
Pramod Kumar answered |
Let 2 equal sides of isoceles right angled triangle be = x
Given,
Area = 8 cm2
so, 8=1/2×x×x
x=√16=4
Now , we have got the the other two sides of the triangle so let's apply Pythagoras theorem to get the length of hypotenuse
Let hypotenuse be = H
4^2+4^2=H^2
16+16=H^2
H=√32=4√2
Given,
Area = 8 cm2
so, 8=1/2×x×x
x=√16=4
Now , we have got the the other two sides of the triangle so let's apply Pythagoras theorem to get the length of hypotenuse
Let hypotenuse be = H
4^2+4^2=H^2
16+16=H^2
H=√32=4√2
The area of a rhombus of 96 cm2. If one of its diagonals is 16 cm, then the length of its side is
- a)6 cm
- b)8 cm
- c)12 cm
- d)10 cm
Correct answer is option 'D'. Can you explain this answer?
The area of a rhombus of 96 cm2. If one of its diagonals is 16 cm, then the length of its side is
a)
6 cm
b)
8 cm
c)
12 cm
d)
10 cm
|
|
Sanjivani Iyer answered |
Given:
Area of rhombus = 96 cm²
One diagonal = 16 cm
To find:
Length of a side of the rhombus
Formula used:
Area of rhombus = (d₁×d₂)/2, where d₁ and d₂ are the diagonals of the rhombus
Explanation:
1. We know that the area of a rhombus is given by the formula:
Area = (d₁×d₂)/2, where d₁ and d₂ are the diagonals of the rhombus.
Substituting the given values, we get:
96 = (16×d₂)/2
Simplifying, we get:
d₂ = (96×2)/16 = 12 cm
2. Now, we know that the diagonals of a rhombus are perpendicular bisectors of each other.
Hence, we can use the Pythagorean theorem to find the length of a side of the rhombus.
3. Let ABCD be a rhombus with diagonals AC and BD intersecting at O. Let OD = 8 cm (half of diagonal BD) and OB = x cm (one side of rhombus). Then, we have:
AO = OC = 8 cm (since diagonals bisect each other)
AB = CD = x (since opposite sides of a rhombus are equal)
Using Pythagoras theorem in triangle AOB, we get:
AB² = AO² + OB²
x² = 8² + x²
Simplifying, we get:
x² - x² = 64
2x² = 64
x² = 32
x = √32 = 4√2
Hence, the length of a side of the rhombus is 4√2 cm.
Therefore, the correct option is (d) 10 cm.
Area of rhombus = 96 cm²
One diagonal = 16 cm
To find:
Length of a side of the rhombus
Formula used:
Area of rhombus = (d₁×d₂)/2, where d₁ and d₂ are the diagonals of the rhombus
Explanation:
1. We know that the area of a rhombus is given by the formula:
Area = (d₁×d₂)/2, where d₁ and d₂ are the diagonals of the rhombus.
Substituting the given values, we get:
96 = (16×d₂)/2
Simplifying, we get:
d₂ = (96×2)/16 = 12 cm
2. Now, we know that the diagonals of a rhombus are perpendicular bisectors of each other.
Hence, we can use the Pythagorean theorem to find the length of a side of the rhombus.
3. Let ABCD be a rhombus with diagonals AC and BD intersecting at O. Let OD = 8 cm (half of diagonal BD) and OB = x cm (one side of rhombus). Then, we have:
AO = OC = 8 cm (since diagonals bisect each other)
AB = CD = x (since opposite sides of a rhombus are equal)
Using Pythagoras theorem in triangle AOB, we get:
AB² = AO² + OB²
x² = 8² + x²
Simplifying, we get:
x² - x² = 64
2x² = 64
x² = 32
x = √32 = 4√2
Hence, the length of a side of the rhombus is 4√2 cm.
Therefore, the correct option is (d) 10 cm.
The area of a triangle is 150 cm2 and its sides are in the ratio 3 : 4 : 5. What is its perimeter?- a)10 cm
- b)30 cm
- c)45 cm
- d)60 cm
Correct answer is option 'D'. Can you explain this answer?
The area of a triangle is 150 cm2 and its sides are in the ratio 3 : 4 : 5. What is its perimeter?
a)
10 cm
b)
30 cm
c)
45 cm
d)
60 cm

|
Samridhi Rane answered |
Here's the solution to your question:
Let coefficient of ratios be X
a = 3x
b = 4x
c = 5x
Using Heron's Formula,
s = (3+4+5)x2 = 12x/2 = 6x

Now,
a = 5*3 = 15 cm
b = 5*4 = 20 cm
c = 5*5 = 25 cm
Perimeter = 15+20+25 = 60 cm
So, Correct Answer is Option D.
You can learn more about Heron's formula by going through the link:
You can learn more about Heron's formula by going through the link:
The area of one triangular part of a rhombus ABCD is given as 125 cm2. The area of rhombus ABCD is- a)625 cm2
- b)500 cm2
- c)250 cm2
- d)2500 cm2
Correct answer is option 'B'. Can you explain this answer?
The area of one triangular part of a rhombus ABCD is given as 125 cm2. The area of rhombus ABCD is
a)
625 cm2
b)
500 cm2
c)
250 cm2
d)
2500 cm2

|
Jyothi Eshwari answered |
Ar one triangle =125cm^2
therefore ar four triangles =125cm^2×4=500cm^2
(since all 4 triangles of rhombus have equal area)
therefore ar four triangles =125cm^2×4=500cm^2
(since all 4 triangles of rhombus have equal area)
A carpenter had to make a triangle with sides 5, 6, 5 units. By mistake he made one with sides 5, 8, 5 units. The difference between their areas is:
a)16 sq unitsb)2 sq unitsc)4 sq unitsd)0 sq unitsCorrect answer is option 'D'. Can you explain this answer?
|
|
Pranjal Gupta answered |
area of actual triangle that he had to make
s = (5+5+6)/2
s= 8
a = √(8 x 3 x 3 x 2)
a1= 12 sq units
area of triangle that the carpenter made
s = (5+5+8)/2
s = 9
a = √(9 x 4 x 4 x 1)
a2 = 12 sq units
so difference a1 - a2 = 12 - 12 =0 sq units
Each side of an equilateral triangle measures 10 cm. Then the area of the triangle is- a)43.3 cm2
- b)43.1 cm2
- c)43.4 cm2
- d)43.2 cm2
Correct answer is option 'A'. Can you explain this answer?
Each side of an equilateral triangle measures 10 cm. Then the area of the triangle is
a)
43.3 cm2
b)
43.1 cm2
c)
43.4 cm2
d)
43.2 cm2
|
|
Kalyan Chauhan answered |
To find the area of an equilateral triangle, we can use the formula:
Area = (√3/4) * side^2
Given that each side of the equilateral triangle measures 10 cm, we can substitute this value into the formula:
Area = (√3/4) * 10^2
Simplifying the equation further:
Area = (√3/4) * 100
Calculating the value of (√3/4):
(√3/4) ≈ 0.433
Substituting this value back into the equation:
Area ≈ 0.433 * 100
Area ≈ 43.3 cm^2
Therefore, the correct answer is option 'A', 43.3 cm^2.
Area = (√3/4) * side^2
Given that each side of the equilateral triangle measures 10 cm, we can substitute this value into the formula:
Area = (√3/4) * 10^2
Simplifying the equation further:
Area = (√3/4) * 100
Calculating the value of (√3/4):
(√3/4) ≈ 0.433
Substituting this value back into the equation:
Area ≈ 0.433 * 100
Area ≈ 43.3 cm^2
Therefore, the correct answer is option 'A', 43.3 cm^2.
If the side of an equilateral triangle is 4 cm, then its area is- a)8√3 m2
- b)4√3 cm2
- c)12√3 cm2
- d)16√3 cm2
Correct answer is option 'B'. Can you explain this answer?
If the side of an equilateral triangle is 4 cm, then its area is
a)
8√3 m2
b)
4√3 cm2
c)
12√3 cm2
d)
16√3 cm2

|
Kaavya Chopra answered |
The area of an equilateral triangle can be found using the formula:
Area = (sqrt(3) / 4) * (side)^2
Plugging in the side length of 4 cm:
Area = (sqrt(3) / 4) * (4)^2
Area = (sqrt(3) / 4) * 16
Area = (1.732 / 4) * 16
Area = 0.433 * 16
Area = 6.928 cm^2
So the correct answer is 6.928 cm^2, not 8 cm^2.
Area = (sqrt(3) / 4) * (side)^2
Plugging in the side length of 4 cm:
Area = (sqrt(3) / 4) * (4)^2
Area = (sqrt(3) / 4) * 16
Area = (1.732 / 4) * 16
Area = 0.433 * 16
Area = 6.928 cm^2
So the correct answer is 6.928 cm^2, not 8 cm^2.
Length of perpendicular drawn on smallest side of scalene triangle is
- a)smallest
- b)No relation
- c)largest
- d)none
Correct answer is option 'C'. Can you explain this answer?
Length of perpendicular drawn on smallest side of scalene triangle is
a)
smallest
b)
No relation
c)
largest
d)
none
|
|
Anuj Sen answered |
Length of perpendicular drawn on smallest side of scalene triangle is always largest.
Semiperimeter of scalene triangle of side k, 2k and 3k is- a)k
- b)3k
- c)4k
- d)2k
Correct answer is option 'B'. Can you explain this answer?
Semiperimeter of scalene triangle of side k, 2k and 3k is
a)
k
b)
3k
c)
4k
d)
2k
|
|
Shraddha Mishra answered |
Introduction:
In this problem, we are given the sides of a scalene triangle as k, 2k, and 3k. We need to find the semiperimeter of this triangle.
Explanation:
To find the semiperimeter of a triangle, we need to add up all the sides of the triangle and divide the sum by 2.
The given sides of the triangle are k, 2k, and 3k.
Step 1:
Add up all the sides of the triangle:
k + 2k + 3k = 6k
Step 2:
Divide the sum by 2 to find the semiperimeter:
Semiperimeter = (6k)/2 = 3k
Conclusion:
Therefore, the semiperimeter of the given scalene triangle with sides k, 2k, and 3k is 3k. The correct answer is option 'B'.
In this problem, we are given the sides of a scalene triangle as k, 2k, and 3k. We need to find the semiperimeter of this triangle.
Explanation:
To find the semiperimeter of a triangle, we need to add up all the sides of the triangle and divide the sum by 2.
The given sides of the triangle are k, 2k, and 3k.
Step 1:
Add up all the sides of the triangle:
k + 2k + 3k = 6k
Step 2:
Divide the sum by 2 to find the semiperimeter:
Semiperimeter = (6k)/2 = 3k
Conclusion:
Therefore, the semiperimeter of the given scalene triangle with sides k, 2k, and 3k is 3k. The correct answer is option 'B'.
Chapter doubts & questions for Heron's Formula - Mathematics (Maths) Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Heron's Formula - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|471 docs|57 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup