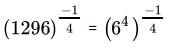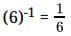All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Sample Papers with Solutions for Class 9 Exam
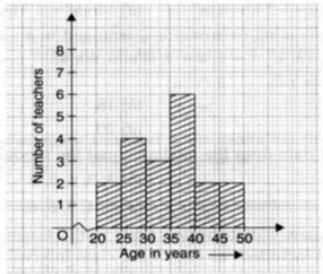
The graph given below shows the frequency distribution of the age of 22 teachers in a school. The number of teachers whose age is less than 40 years is
- a)17
- b)16
- c)15
- d)14
Correct answer is option 'C'. Can you explain this answer?
The graph given below shows the frequency distribution of the age of 22 teachers in a school. The number of teachers whose age is less than 40 years is


a)
17
b)
16
c)
15
d)
14

|
Gunjan Lakhani answered |
Add the values corresponding to the height of the bar before 40.
6 + 3 + 4 + 2 = 15
6 + 3 + 4 + 2 = 15
If (a, -2) lies on the graph of 3x - y = 10, then the value of a is
- a)8/3
- b)0
- c)4
- d)1
Correct answer is option 'A'. Can you explain this answer?
If (a, -2) lies on the graph of 3x - y = 10, then the value of a is
a)
8/3
b)
0
c)
4
d)
1
|
|
Meera Rana answered |
(a, -2) lies on the graph of 3x - y = 10
3(a) - (-2) = 10
3a + 2 = 10
3a = 10-2
3a = 8
a = 8/3
3(a) - (-2) = 10
3a + 2 = 10
3a = 10-2
3a = 8
a = 8/3
Which one of the following statements is true?- a)The sum of two irrational numbers may be a rational number or an irrational number
- b)The sum of two irrational numbers is always an integer
- c)The sum of two irrational numbers is always an irrational number
- d)The sum of two irrational numbers is always a rational number
Correct answer is option 'A'. Can you explain this answer?
Which one of the following statements is true?
a)
The sum of two irrational numbers may be a rational number or an irrational number
b)
The sum of two irrational numbers is always an integer
c)
The sum of two irrational numbers is always an irrational number
d)
The sum of two irrational numbers is always a rational number
|
|
Rohit Sharma answered |
The sum of two irrational numbers may be a rational number or an irrational number
Eg. a = √2 (which is irrational)
b = 2√2(which is irrational)
a + b = √2 + 2√2 = 3√2 ( which is irrational)
and Let a = 1+√2 (which is irrational)
and b= 1- √2 (which is irrational)
Now, a + b = 1+√2 +1- √2
= 2 (which is rational)
Eg. a = √2 (which is irrational)
b = 2√2(which is irrational)
a + b = √2 + 2√2 = 3√2 ( which is irrational)
and Let a = 1+√2 (which is irrational)
and b= 1- √2 (which is irrational)
Now, a + b = 1+√2 +1- √2
= 2 (which is rational)
The co-ordinates of a point above the x-axis lying on y-axis at a distance of 4 units are- a)(0, -4)
- b)4, 0)
- c)(0, 4)
- d)(-4, 0)
Correct answer is option 'C'. Can you explain this answer?
The co-ordinates of a point above the x-axis lying on y-axis at a distance of 4 units are
a)
(0, -4)
b)
4, 0)
c)
(0, 4)
d)
(-4, 0)
|
|
Swati Verma answered |
It lies on y-axis so it's abscissa = 0 and it lies on y-axis at a distance of 4unit.
Thus point will be (0, 4).
Thus point will be (0, 4).
Read the text carefully and answer the questions:
Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the second angle?- a)60°
- b)45°
- c)30°
- d)90°
Correct answer is option 'D'. Can you explain this answer?
Read the text carefully and answer the questions:

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the second angle?

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the second angle?
a)
60°
b)
45°
c)
30°
d)
90°
|
|
Radha Iyer answered |
90°
The mean of six numbers is 23. If one of the numbers is excluded, the mean of the remaining numbers becomes 20. The excluded number is- a)37
- b)39
- c)38
- d)36
Correct answer is option 'C'. Can you explain this answer?
The mean of six numbers is 23. If one of the numbers is excluded, the mean of the remaining numbers becomes 20. The excluded number is
a)
37
b)
39
c)
38
d)
36
|
|
Aditi Sharma answered |
The mean of the six numbers is 23.
So the sum of six numbers is 23 x 6 = 138
After excluding one number, the mean of the remaining numbers is 20.
So the sum of five numbers is 20 x 5 = 100
The difference between them is
138 - 100 = 38
So the sum of six numbers is 23 x 6 = 138
After excluding one number, the mean of the remaining numbers is 20.
So the sum of five numbers is 20 x 5 = 100
The difference between them is
138 - 100 = 38
How many linear equations are satisfied by x = 2 and y = - 3?- a)Infinitely many
- b)Only one
- c)Three
- d)Two
Correct answer is option 'A'. Can you explain this answer?
How many linear equations are satisfied by x = 2 and y = - 3?
a)
Infinitely many
b)
Only one
c)
Three
d)
Two
|
|
Aniket Gupta answered |
Explanation:
To determine how many linear equations are satisfied by x = 2 and y = -3, we need to find the number of equations that are true when these values are substituted into the equations.
Step 1: Understanding Linear Equations
A linear equation is an equation of the form Ax + By = C, where A, B, and C are constants, and x and y are variables. The equation represents a straight line on a coordinate plane.
Step 2: Substituting the values
We are given x = 2 and y = -3. To find the number of equations satisfied by these values, we substitute these values into each equation and check if the equation holds true.
Step 3: Analyzing the Equations
Let's consider an example equation: 3x - 2y = 8
Substituting x = 2 and y = -3 into the equation, we have:
3(2) - 2(-3) = 8
6 + 6 = 8
12 = 8
Since 12 is not equal to 8, the equation 3x - 2y = 8 is not satisfied by x = 2 and y = -3.
Step 4: Conclusion
We can repeat this process for other linear equations, and we will find that none of the linear equations are satisfied by x = 2 and y = -3. Therefore, there are no linear equations satisfied by these values.
The correct answer is option 'A': Infinitely many.
To determine how many linear equations are satisfied by x = 2 and y = -3, we need to find the number of equations that are true when these values are substituted into the equations.
Step 1: Understanding Linear Equations
A linear equation is an equation of the form Ax + By = C, where A, B, and C are constants, and x and y are variables. The equation represents a straight line on a coordinate plane.
Step 2: Substituting the values
We are given x = 2 and y = -3. To find the number of equations satisfied by these values, we substitute these values into each equation and check if the equation holds true.
Step 3: Analyzing the Equations
Let's consider an example equation: 3x - 2y = 8
Substituting x = 2 and y = -3 into the equation, we have:
3(2) - 2(-3) = 8
6 + 6 = 8
12 = 8
Since 12 is not equal to 8, the equation 3x - 2y = 8 is not satisfied by x = 2 and y = -3.
Step 4: Conclusion
We can repeat this process for other linear equations, and we will find that none of the linear equations are satisfied by x = 2 and y = -3. Therefore, there are no linear equations satisfied by these values.
The correct answer is option 'A': Infinitely many.
The lengths of the sides of ABCare consecutive integers. It ΔABC has perimeter as an equilateral triangle triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?- a)8
- b)10
- c)4
- d)6
Correct answer is option 'A'. Can you explain this answer?
The lengths of the sides of ABCare consecutive integers. It ΔABC has perimeter as an equilateral triangle triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
a)
8
b)
10
c)
4
d)
6
|
|
Swati Verma answered |
Let the sides of ΔABC be n, n + 1, n + 2
⇒ Perimeter = n + n + 1 + n + 2
⇒ (9 + 9 + 9) = 3n + 3
⇒ 27 = 3n + 3
⇒ 3n = 24
⇒ n = 8 cm
Thus, the shortest side is 8 cm
⇒ Perimeter = n + n + 1 + n + 2
⇒ (9 + 9 + 9) = 3n + 3
⇒ 27 = 3n + 3
⇒ 3n = 24
⇒ n = 8 cm
Thus, the shortest side is 8 cm
The equation 2x + 5y = 7 has a unique solution, if x, y are :- a)Rational numbers
- b)Real numbers
- c)Natural numbers
- d)Positive real numbers
Correct answer is option 'C'. Can you explain this answer?
The equation 2x + 5y = 7 has a unique solution, if x, y are :
a)
Rational numbers
b)
Real numbers
c)
Natural numbers
d)
Positive real numbers
|
|
Aditi Sharma answered |
There is only one pair i.e., (1, 1) which satisfies the given equation but in positive real numbers, real numbers and rational numbers there are many pairs to satisfy the given linear equation. Hence, unique solution is possible only in case of Natural numbers.
If side of a scalene Δ is doubled then area would be increased by- a)200%
- b)25%
- c)50%
- d)300%
Correct answer is option 'D'. Can you explain this answer?
If side of a scalene Δ is doubled then area would be increased by
a)
200%
b)
25%
c)
50%
d)
300%
|
|
Pranali Patel answered |
Explanation:
Initial Area of Scalene Triangle:
- Let the sides of the scalene triangle be a, b, and c.
- The area of a scalene triangle can be found using Heron's formula:
Area = √(s(s-a)(s-b)(s-c)), where s = (a + b + c) / 2.
- Let the initial area of the triangle be A.
Area of Doubled Triangle:
- If the side of the scalene triangle is doubled, the new sides would be 2a, 2b, and 2c.
- The new area of the triangle can be found using Heron's formula with the new sides.
- Let the new area of the triangle be A'.
Calculating the Increase in Area:
- The percentage increase in area can be calculated using the formula:
Percentage Increase = ((A' - A) / A) * 100%.
Solving the Problem:
- Since the sides of the triangle are doubled, the new sides are 2a, 2b, and 2c.
- The new area, A', can be calculated using Heron's formula with the new sides.
- The percentage increase in area can then be calculated using the formula mentioned above.
- Upon calculation, it is found that the area is increased by 300%.
Therefore, the correct answer is option 'D' - 300%.
Initial Area of Scalene Triangle:
- Let the sides of the scalene triangle be a, b, and c.
- The area of a scalene triangle can be found using Heron's formula:
Area = √(s(s-a)(s-b)(s-c)), where s = (a + b + c) / 2.
- Let the initial area of the triangle be A.
Area of Doubled Triangle:
- If the side of the scalene triangle is doubled, the new sides would be 2a, 2b, and 2c.
- The new area of the triangle can be found using Heron's formula with the new sides.
- Let the new area of the triangle be A'.
Calculating the Increase in Area:
- The percentage increase in area can be calculated using the formula:
Percentage Increase = ((A' - A) / A) * 100%.
Solving the Problem:
- Since the sides of the triangle are doubled, the new sides are 2a, 2b, and 2c.
- The new area, A', can be calculated using Heron's formula with the new sides.
- The percentage increase in area can then be calculated using the formula mentioned above.
- Upon calculation, it is found that the area is increased by 300%.
Therefore, the correct answer is option 'D' - 300%.
Read the text carefully and answer the questions:
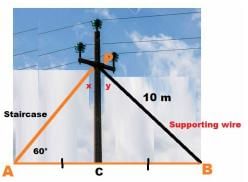
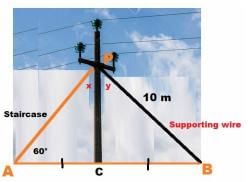
As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
What is the value of ∠PBC?- a)45°
- b)90°
- c)60°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
Read the text carefully and answer the questions:

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
What is the value of ∠PBC?

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
What is the value of ∠PBC?
a)
45°
b)
90°
c)
60°
d)
30°
|
|
Arun Sharma answered |
45°
The marks obtained by 17 students in a mathematics test (out of 100) are given below :
91, 82, 100, 100, 96, 65, 82, 76, 79, 90, 46, 64, 72, 68, 66, 48, 49.
Find the range of the data.- a)90
- b)100
- c)46
- d)54
Correct answer is option 'D'. Can you explain this answer?
The marks obtained by 17 students in a mathematics test (out of 100) are given below :
91, 82, 100, 100, 96, 65, 82, 76, 79, 90, 46, 64, 72, 68, 66, 48, 49.
Find the range of the data.
91, 82, 100, 100, 96, 65, 82, 76, 79, 90, 46, 64, 72, 68, 66, 48, 49.
Find the range of the data.
a)
90
b)
100
c)
46
d)
54
|
|
Anita Menon answered |
Highest Marks = 100
Lowest Marks = 46
Range of data = 100 - 46 = 54
Lowest Marks = 46
Range of data = 100 - 46 = 54
If √5n = 125,then 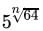 =
= - a)1/5
- b)25
- c)1/625
- d)625
Correct answer is option 'B'. Can you explain this answer?
If √5n = 125,then 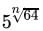 =
=
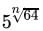 =
= a)
1/5
b)
25
c)
1/625
d)
625
|
|
Meera Rana answered |
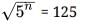
⇒

Comparing, we get
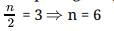
Now
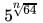
=
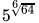
=
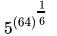
=
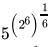
=
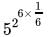
= 52
= 25
The mid-value of a class interval is 42. If the class size is 10, then the upper and lower limits of the class are:- a)47.5 and 37.5
- b)47 and 37
- c)37.5 and 47.5
- d)37 and 47
Correct answer is option 'B'. Can you explain this answer?
The mid-value of a class interval is 42. If the class size is 10, then the upper and lower limits of the class are:
a)
47.5 and 37.5
b)
47 and 37
c)
37.5 and 47.5
d)
37 and 47
|
|
Swati Verma answered |
Let the lower limit of a class = x
class size = 10
Upper limit = x + 10
Now, mid - value =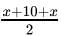 = x + 5 = 42 (given)
= x + 5 = 42 (given)
x = 37 = lower limit
x + 10 = 47 = upper limit
pper and lower limits are 47, 37
class size = 10
Upper limit = x + 10
Now, mid - value =
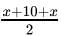 = x + 5 = 42 (given)
= x + 5 = 42 (given)x = 37 = lower limit
x + 10 = 47 = upper limit
pper and lower limits are 47, 37
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is- a)60 m
- b)66 m
- c)11 m
- d)50 m
Correct answer is option 'A'. Can you explain this answer?
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
a)
60 m
b)
66 m
c)
11 m
d)
50 m
|
|
Kalyan Rane answered |
Explanation:
Given:
- Sides of the triangle: 11 m, 60 m, and 61 m
Altitude to the smallest side:
To find the altitude to the smallest side of the triangle, we can use the formula for the area of a triangle: Area = 1/2 * base * height.
Calculations:
Since the smallest side of the triangle is 11 m, we can consider the altitude to this side as the height of the triangle.
Using the formula for the area of a triangle and the given sides, we can calculate the area of the triangle as follows:
Area = 1/2 * 11 * height (where height is the altitude to the smallest side)
Since the area of the triangle can also be calculated using Heron's formula, which is given by:
Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter of the triangle and a, b, c are the sides of the triangle.
By substituting the given values, we get:
s = (11 + 60 + 61)/2 = 132/2 = 66
Area = √[66(66-11)(66-60)(66-61)]
Area = √[66*55*6*5]
Area = √(108900) = 330
Now, equating the two expressions for the area of the triangle, we get:
1/2 * 11 * height = 330
height = 330 / (1/2 * 11) = 60 m
Therefore, the altitude to the smallest side of the triangle is 60 m. Hence, the correct answer is option 'A'.
Given:
- Sides of the triangle: 11 m, 60 m, and 61 m
Altitude to the smallest side:
To find the altitude to the smallest side of the triangle, we can use the formula for the area of a triangle: Area = 1/2 * base * height.
Calculations:
Since the smallest side of the triangle is 11 m, we can consider the altitude to this side as the height of the triangle.
Using the formula for the area of a triangle and the given sides, we can calculate the area of the triangle as follows:
Area = 1/2 * 11 * height (where height is the altitude to the smallest side)
Since the area of the triangle can also be calculated using Heron's formula, which is given by:
Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter of the triangle and a, b, c are the sides of the triangle.
By substituting the given values, we get:
s = (11 + 60 + 61)/2 = 132/2 = 66
Area = √[66(66-11)(66-60)(66-61)]
Area = √[66*55*6*5]
Area = √(108900) = 330
Now, equating the two expressions for the area of the triangle, we get:
1/2 * 11 * height = 330
height = 330 / (1/2 * 11) = 60 m
Therefore, the altitude to the smallest side of the triangle is 60 m. Hence, the correct answer is option 'A'.
If 4x - 4x-1 = 24, then (2x)x equals- a)√5
- b)25√5
- c)125
- d)5√5
Correct answer is option 'B'. Can you explain this answer?
If 4x - 4x-1 = 24, then (2x)x equals
a)
√5
b)
25√5
c)
125
d)
5√5
|
|
Swati Verma answered |
4x - 4x-1 = 24
⇒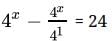
⇒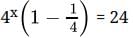
⇒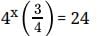
⇒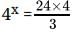
4x = 32
(22)x = (2)5
22x = 25
Comparing, we get
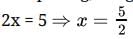
=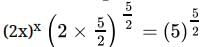
=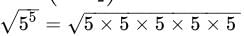
=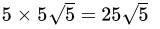
⇒
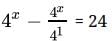
⇒
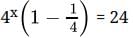
⇒
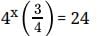
⇒
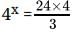
4x = 32
(22)x = (2)5
22x = 25
Comparing, we get
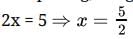
=
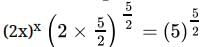
=
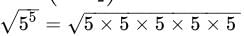
=
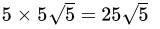
In a grouped frequency distribution, the class intervals are 0-10, 10-20, 20-30, .., then the class width is- a)30
- b)10
- c)15
- d)20
Correct answer is option 'B'. Can you explain this answer?
In a grouped frequency distribution, the class intervals are 0-10, 10-20, 20-30, .., then the class width is
a)
30
b)
10
c)
15
d)
20
|
|
Neha Tiwari answered |
Grouped Frequency Distribution
A grouped frequency distribution is a way to organize and present data in a tabular form. It is particularly useful when dealing with a large set of data, as it helps in summarizing the data and identifying patterns or trends. In a grouped frequency distribution, the data is grouped into intervals or classes, and the frequency of each interval is recorded.
Class Intervals
In the given question, the class intervals are 0-10, 10-20, 20-30, and so on. Each class interval represents a range of values that the data falls into. The lower limit of the class interval is the smallest value that falls into that interval, and the upper limit is the largest value that falls into that interval. For example, in the class interval 0-10, the lower limit is 0 and the upper limit is 10.
Class Width
The class width is the difference between the upper and lower limits of a class interval. It represents the range of values that each interval covers. In the given question, the class intervals are consecutive and have a constant difference of 10. Therefore, the class width is 10.
Explanation of Options
a) 30: This option is not correct as it does not represent the class width. The class width is 10, not 30.
b) 10: This option is correct as it represents the class width. The class width is indeed 10.
c) 15: This option is not correct as it does not represent the class width. The class width is 10, not 15.
d) 20: This option is not correct as it does not represent the class width. The class width is 10, not 20.
Conclusion
In a grouped frequency distribution with class intervals of 0-10, 10-20, 20-30, and so on, the class width is 10. This represents the range of values covered by each interval and is different from the difference between consecutive intervals.
A grouped frequency distribution is a way to organize and present data in a tabular form. It is particularly useful when dealing with a large set of data, as it helps in summarizing the data and identifying patterns or trends. In a grouped frequency distribution, the data is grouped into intervals or classes, and the frequency of each interval is recorded.
Class Intervals
In the given question, the class intervals are 0-10, 10-20, 20-30, and so on. Each class interval represents a range of values that the data falls into. The lower limit of the class interval is the smallest value that falls into that interval, and the upper limit is the largest value that falls into that interval. For example, in the class interval 0-10, the lower limit is 0 and the upper limit is 10.
Class Width
The class width is the difference between the upper and lower limits of a class interval. It represents the range of values that each interval covers. In the given question, the class intervals are consecutive and have a constant difference of 10. Therefore, the class width is 10.
Explanation of Options
a) 30: This option is not correct as it does not represent the class width. The class width is 10, not 30.
b) 10: This option is correct as it represents the class width. The class width is indeed 10.
c) 15: This option is not correct as it does not represent the class width. The class width is 10, not 15.
d) 20: This option is not correct as it does not represent the class width. The class width is 10, not 20.
Conclusion
In a grouped frequency distribution with class intervals of 0-10, 10-20, 20-30, and so on, the class width is 10. This represents the range of values covered by each interval and is different from the difference between consecutive intervals.
The mean weight of six boys in a group is 48 kg. The individual weights of five of them are 51 kg, 45 kg, 49 kg, 46 kg and 44 kg. The weight of the 6th boy is- a)52.8 kg
- b)52 kg
- c)47 kg
- d)53 kg
Correct answer is option 'D'. Can you explain this answer?
The mean weight of six boys in a group is 48 kg. The individual weights of five of them are 51 kg, 45 kg, 49 kg, 46 kg and 44 kg. The weight of the 6th boy is
a)
52.8 kg
b)
52 kg
c)
47 kg
d)
53 kg
|
|
Raj Malik answered |
Understanding the Problem
The question states that the mean weight of six boys is 48 kg. This means that the total weight of all six boys can be calculated using the formula for mean:
- Mean = Total Weight / Number of Boys
- Total Weight = Mean * Number of Boys
- Total Weight = 48 kg * 6 = 288 kg
Calculating the Total Weight of Five Boys
We have the individual weights of five boys:
- Boy 1: 51 kg
- Boy 2: 45 kg
- Boy 3: 49 kg
- Boy 4: 46 kg
- Boy 5: 44 kg
Now, we calculate the total weight of these five boys:
- Total Weight of Five Boys = 51 + 45 + 49 + 46 + 44
- Total Weight of Five Boys = 235 kg
Finding the Weight of the 6th Boy
To find the weight of the 6th boy, we subtract the total weight of the first five boys from the total weight of all six boys:
- Weight of 6th Boy = Total Weight of Six Boys - Total Weight of Five Boys
- Weight of 6th Boy = 288 kg - 235 kg
- Weight of 6th Boy = 53 kg
Conclusion
Thus, the weight of the 6th boy is 53 kg, which corresponds to option 'D'.
The question states that the mean weight of six boys is 48 kg. This means that the total weight of all six boys can be calculated using the formula for mean:
- Mean = Total Weight / Number of Boys
- Total Weight = Mean * Number of Boys
- Total Weight = 48 kg * 6 = 288 kg
Calculating the Total Weight of Five Boys
We have the individual weights of five boys:
- Boy 1: 51 kg
- Boy 2: 45 kg
- Boy 3: 49 kg
- Boy 4: 46 kg
- Boy 5: 44 kg
Now, we calculate the total weight of these five boys:
- Total Weight of Five Boys = 51 + 45 + 49 + 46 + 44
- Total Weight of Five Boys = 235 kg
Finding the Weight of the 6th Boy
To find the weight of the 6th boy, we subtract the total weight of the first five boys from the total weight of all six boys:
- Weight of 6th Boy = Total Weight of Six Boys - Total Weight of Five Boys
- Weight of 6th Boy = 288 kg - 235 kg
- Weight of 6th Boy = 53 kg
Conclusion
Thus, the weight of the 6th boy is 53 kg, which corresponds to option 'D'.
In a histogram the area of each rectangle is proportional to- a)the class size of the corresponding class interval
- b)cumulative frequency of the corresponding class interval
- c)the class mark of the corresponding class interval
- d)frequency of the corresponding class interval
Correct answer is option 'D'. Can you explain this answer?
In a histogram the area of each rectangle is proportional to
a)
the class size of the corresponding class interval
b)
cumulative frequency of the corresponding class interval
c)
the class mark of the corresponding class interval
d)
frequency of the corresponding class interval
|
|
Aditi Sharma answered |
A histogram is a display of statistical information that uses rectangles to show the frequency of data items in successive numerical intervals of equal size. In the most common form of histogram, the independent variable is plotted along the horizontal axis and the dependent variable is plotted along the vertical axis.
Read the text carefully and answer the questions:
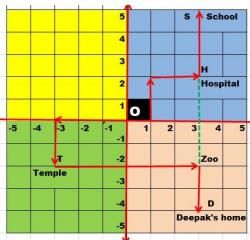
In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What are the coordinates of the Hospital?- a)(2, 3)
- b)(5, 5)
- c)(3, 2)
- d)(3, 3)
Correct answer is option 'C'. Can you explain this answer?
Read the text carefully and answer the questions:

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What are the coordinates of the Hospital?

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What are the coordinates of the Hospital?
a)
(2, 3)
b)
(5, 5)
c)
(3, 2)
d)
(3, 3)
|
|
Aditya Shah answered |
(3, 2)
In ΔABC and ΔPQR. If AB = QP, ∠B = ∠P , BC = PR then which one of the following congruence conditions applies:- a)SAS
- b)SSS
- c)ASA
- d)RHS
Correct answer is option 'A'. Can you explain this answer?
In ΔABC and ΔPQR. If AB = QP, ∠B = ∠P , BC = PR then which one of the following congruence conditions applies:
a)
SAS
b)
SSS
c)
ASA
d)
RHS
|
|
Siya Shah answered |
Understanding Congruence in Triangles
In the given problem, we need to identify which congruence condition applies between triangles ABC and PQR.
Given Information:
- AB = QP
- ∠B = ∠P
- BC = PR
Analyzing the Conditions:
- Side AB = Side QP: This indicates that one pair of corresponding sides are equal.
- Angle ∠B = Angle ∠P: This shows that one pair of corresponding angles are equal.
- Side BC = Side PR: This indicates that another pair of corresponding sides are also equal.
Applying the SAS Congruence Condition:
The SAS (Side-Angle-Side) congruence condition states that if two sides and the angle between them in one triangle are equal to two sides and the included angle in another triangle, then the triangles are congruent.
- Here, we have:
- One side (AB) equal to another side (QP)
- The angle (∠B) between those sides equal to (∠P)
- And the second side (BC) equal to the second side (PR)
Thus, we can conclude that triangles ABC and PQR are congruent by the SAS condition.
Conclusion:
Therefore, the correct answer is option 'A' – SAS. This condition effectively demonstrates the congruence between the two triangles based on the information provided.
In the given problem, we need to identify which congruence condition applies between triangles ABC and PQR.
Given Information:
- AB = QP
- ∠B = ∠P
- BC = PR
Analyzing the Conditions:
- Side AB = Side QP: This indicates that one pair of corresponding sides are equal.
- Angle ∠B = Angle ∠P: This shows that one pair of corresponding angles are equal.
- Side BC = Side PR: This indicates that another pair of corresponding sides are also equal.
Applying the SAS Congruence Condition:
The SAS (Side-Angle-Side) congruence condition states that if two sides and the angle between them in one triangle are equal to two sides and the included angle in another triangle, then the triangles are congruent.
- Here, we have:
- One side (AB) equal to another side (QP)
- The angle (∠B) between those sides equal to (∠P)
- And the second side (BC) equal to the second side (PR)
Thus, we can conclude that triangles ABC and PQR are congruent by the SAS condition.
Conclusion:
Therefore, the correct answer is option 'A' – SAS. This condition effectively demonstrates the congruence between the two triangles based on the information provided.
If (2, 0) is a solution of the linear equation 2x + 3y = k, then the value of k is- a)2
- b)4
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
If (2, 0) is a solution of the linear equation 2x + 3y = k, then the value of k is
a)
2
b)
4
c)
5
d)
6
|
|
Aditi Sharma answered |
(2, 0) is a solution of the linear equation 2x + 3y = k
⇒ 4 = k
⇒ 4 = k
Write the linear equation such that each point on its graph has an ordinate 5 times its abscissa- a)y = 5x
- b)none of these
- c)5x + y = 2
- d)x = 5y
Correct answer is option 'A'. Can you explain this answer?
Write the linear equation such that each point on its graph has an ordinate 5 times its abscissa
a)
y = 5x
b)
none of these
c)
5x + y = 2
d)
x = 5y
|
|
Swati Verma answered |
y = 5x
at x = 1
y = 5.1 = 5
y = 5
(1,5)
at x = 2
y = 5.2 = 10
y = 10
(2,10)
at x = 3
y = 5.3 = 15
y = 15
(3,15)
at x = 1
y = 5.1 = 5
y = 5
(1,5)
at x = 2
y = 5.2 = 10
y = 10
(2,10)
at x = 3
y = 5.3 = 15
y = 15
(3,15)
The base of an isosceles triangle is 8 cm long and each of its equal sides measures 6 cm. The area of the triangle is- a)8√5 cm2
- b)8√3 cm2
- c)16√3 cm2
- d)16√5 cm2
Correct answer is option 'A'. Can you explain this answer?
The base of an isosceles triangle is 8 cm long and each of its equal sides measures 6 cm. The area of the triangle is
a)
8√5 cm2
b)
8√3 cm2
c)
16√3 cm2
d)
16√5 cm2
|
|
Swati Verma answered |
Area of isosceles triangle = 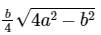
Here, a = 6 cm and b = 8 cm
Thus, we have
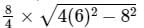
=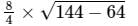
=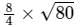
=
= 8√5 cm2
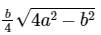
Here, a = 6 cm and b = 8 cm
Thus, we have
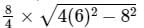
=
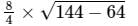
=
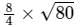
=
= 8√5 cm2
Read the text carefully and answer the questions:
As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the ΔPAC and ΔPBC which angles are given to be equal?- a)none of these
- b)∠B = ∠y
- c)∠B = ∠x
- d)∠A = ∠x
Correct answer is option 'C'. Can you explain this answer?
Read the text carefully and answer the questions:

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the ΔPAC and ΔPBC which angles are given to be equal?

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the ΔPAC and ΔPBC which angles are given to be equal?
a)
none of these
b)
∠B = ∠y
c)
∠B = ∠x
d)
∠A = ∠x
|
|
Anita Menon answered |
∠B = ∠x
If all the altitudes from the vertices to the opposite sides of a triangle are equal, then the triangle is- a)Equilateral
- b)Isosceles
- c)Scalene
- d)Right-angled
Correct answer is option 'A'. Can you explain this answer?
If all the altitudes from the vertices to the opposite sides of a triangle are equal, then the triangle is
a)
Equilateral
b)
Isosceles
c)
Scalene
d)
Right-angled
|
|
Swati Verma answered |
In an equilateral triangle all the altitudes, sides, angles, perpendicular bisectors, medians and angular bisectors are equal.
Which is true?- a)A triangle can have two obtuse angles
- b)A triangle can have two right angles.
- c)An exterior angle of a triangle is less than either of the interior opposite angles.
- d)A triangle can have two acute angles.
Correct answer is option 'D'. Can you explain this answer?
Which is true?
a)
A triangle can have two obtuse angles
b)
A triangle can have two right angles.
c)
An exterior angle of a triangle is less than either of the interior opposite angles.
d)
A triangle can have two acute angles.
|
|
Aditi Sharma answered |
True, you may have a triangle with two or more acute angles. If a triangle has three acute angles, the triangle is called an Acute Triangle. If a triangle has two acute angles and a single obtuse angle, the triangle is called an Obtuse Triangle.
Read the text carefully and answer the questions:

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the sum of all three angles measured by Ashok using Dee?- a)180°
- b)100°
- c)270°
- d)90°
Correct answer is option 'A'. Can you explain this answer?
Read the text carefully and answer the questions:

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the sum of all three angles measured by Ashok using Dee?

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the sum of all three angles measured by Ashok using Dee?
a)
180°
b)
100°
c)
270°
d)
90°
|
|
Aditi Sharma answered |
180°
How many linear equations can be satisfied by x = 2 and y = 3?- a)only one
- b)none of these
- c)many
- d)two
Correct answer is option 'C'. Can you explain this answer?
How many linear equations can be satisfied by x = 2 and y = 3?
a)
only one
b)
none of these
c)
many
d)
two
|
|
Yashvi Chawla answered |
Explanation:
Given:
x = 2, y = 3
Linear Equations:
Linear equations are equations of the form ax + by = c, where a, b, and c are constants.
Number of Equations:
When x = 2 and y = 3, these values can satisfy many linear equations. This is because there are infinite number of linear equations that can have x = 2 and y = 3 as solutions.
Example Equations:
- 2x + 3y = 13
- x + 2y = 8
- 3x - y = 4
Explanation of Answer:
The values x = 2 and y = 3 can satisfy an infinite number of linear equations because any equation that holds true for x = 2 and y = 3 is a valid solution. Therefore, the correct answer is option 'C' - many.
Given:
x = 2, y = 3
Linear Equations:
Linear equations are equations of the form ax + by = c, where a, b, and c are constants.
Number of Equations:
When x = 2 and y = 3, these values can satisfy many linear equations. This is because there are infinite number of linear equations that can have x = 2 and y = 3 as solutions.
Example Equations:
- 2x + 3y = 13
- x + 2y = 8
- 3x - y = 4
Explanation of Answer:
The values x = 2 and y = 3 can satisfy an infinite number of linear equations because any equation that holds true for x = 2 and y = 3 is a valid solution. Therefore, the correct answer is option 'C' - many.
If 102y = 25, then 10-y equals
- a)-1/5
- b)1/5
- c)1/625
- d)1/50
Correct answer is option 'B'. Can you explain this answer?
If 102y = 25, then 10-y equals
a)
-1/5
b)
1/5
c)
1/625
d)
1/50
|
|
Swati Verma answered |
102y = 25
102y = 25
(10y)2 = (5)2
⇒ 10y = 5
Now 10-y
= 1/10y
= 1/5
102y = 25
(10y)2 = (5)2
⇒ 10y = 5
Now 10-y
= 1/10y
= 1/5
The graph of y = 5 is a line- a)making an intercept 5 on the x-axis
- b)parallel to the y-axis at a distance of 5 units from the origin
- c)parallel to the x-axis at a distance of 6 units from the origin
- d)making an intercept 5 on the y-axis
Correct answer is option 'D'. Can you explain this answer?
The graph of y = 5 is a line
a)
making an intercept 5 on the x-axis
b)
parallel to the y-axis at a distance of 5 units from the origin
c)
parallel to the x-axis at a distance of 6 units from the origin
d)
making an intercept 5 on the y-axis
|
|
Swati Verma answered |
As, the graph of y = 5 is a line parallel to x-axis i.e. y = 0.
⇒ The line represented by the equation y = 5 is parallel to x-axis and intersects y-axis at y = 5.
So, the graph of y = 5 is a line parallel to the x-axis at a distance of 5 units from the origin making an intercept 5 on the y-axis.
⇒ The line represented by the equation y = 5 is parallel to x-axis and intersects y-axis at y = 5.
So, the graph of y = 5 is a line parallel to the x-axis at a distance of 5 units from the origin making an intercept 5 on the y-axis.
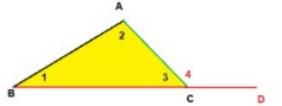
The exterior angle of a triangle is equal to the sum of two- a)alternate angles.
- b)interior angles
- c)exterior angles
- d)interior opposite angles
Correct answer is option 'D'. Can you explain this answer?
The exterior angle of a triangle is equal to the sum of two
a)
alternate angles.
b)
interior angles
c)
exterior angles
d)
interior opposite angles
|
|
Aditi Sharma answered |
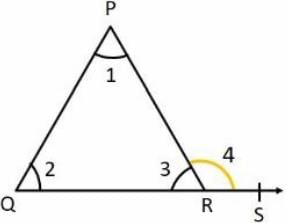
∠1 + ∠2 + ∠3 = 180o (Angle sum property)....(a)
∠3 + ∠4 = 180o (Linear Pair)....(b)
On equating equations a and b, we get
∠1 + ∠2 = ∠4
The number of angles formed by a transversal with a pair of parallel lines are
- a)4
- b)8
- c)6
- d)3
Correct answer is option 'B'. Can you explain this answer?
The number of angles formed by a transversal with a pair of parallel lines are
a)
4
b)
8
c)
6
d)
3
|
|
Samaira Kapoor answered |
Introduction:
When a transversal intersects a pair of parallel lines, it forms various angles. These angles have specific properties and relationships. In this case, we need to determine the number of angles formed by a transversal with a pair of parallel lines.
Explanation:
When a transversal intersects a pair of parallel lines, it forms eight angles. Let's label these angles for better understanding:
1. Alternate Interior Angles: These angles are formed on opposite sides of the transversal and inside the parallel lines.
- Angle 1 and Angle 5 are alternate interior angles.
- Angle 3 and Angle 7 are alternate interior angles.
2. Alternate Exterior Angles: These angles are formed on opposite sides of the transversal and outside the parallel lines.
- Angle 2 and Angle 6 are alternate exterior angles.
- Angle 4 and Angle 8 are alternate exterior angles.
3. Corresponding Angles: These angles are formed on the same side of the transversal and in the same position relative to the parallel lines.
- Angle 1 and Angle 3 are corresponding angles.
- Angle 2 and Angle 4 are corresponding angles.
- Angle 5 and Angle 7 are corresponding angles.
- Angle 6 and Angle 8 are corresponding angles.
4. Consecutive Interior Angles: These angles are formed on the same side of the transversal and inside the parallel lines.
- Angle 3 and Angle 5 are consecutive interior angles.
- Angle 7 and Angle 1 are consecutive interior angles.
Summary:
In total, there are eight angles formed by a transversal with a pair of parallel lines. These include four pairs of alternate interior/exterior angles and four pairs of corresponding angles. Therefore, the correct answer is option 'B' - 8.
When a transversal intersects a pair of parallel lines, it forms various angles. These angles have specific properties and relationships. In this case, we need to determine the number of angles formed by a transversal with a pair of parallel lines.
Explanation:
When a transversal intersects a pair of parallel lines, it forms eight angles. Let's label these angles for better understanding:
1. Alternate Interior Angles: These angles are formed on opposite sides of the transversal and inside the parallel lines.
- Angle 1 and Angle 5 are alternate interior angles.
- Angle 3 and Angle 7 are alternate interior angles.
2. Alternate Exterior Angles: These angles are formed on opposite sides of the transversal and outside the parallel lines.
- Angle 2 and Angle 6 are alternate exterior angles.
- Angle 4 and Angle 8 are alternate exterior angles.
3. Corresponding Angles: These angles are formed on the same side of the transversal and in the same position relative to the parallel lines.
- Angle 1 and Angle 3 are corresponding angles.
- Angle 2 and Angle 4 are corresponding angles.
- Angle 5 and Angle 7 are corresponding angles.
- Angle 6 and Angle 8 are corresponding angles.
4. Consecutive Interior Angles: These angles are formed on the same side of the transversal and inside the parallel lines.
- Angle 3 and Angle 5 are consecutive interior angles.
- Angle 7 and Angle 1 are consecutive interior angles.
Summary:
In total, there are eight angles formed by a transversal with a pair of parallel lines. These include four pairs of alternate interior/exterior angles and four pairs of corresponding angles. Therefore, the correct answer is option 'B' - 8.
Read the text carefully and answer the questions:
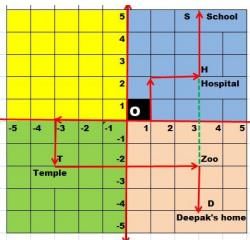
In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What is the common ordinate of temple and Zoo?- a)5
- b)-2
- c)-3
- d)3
Correct answer is option 'B'. Can you explain this answer?
Read the text carefully and answer the questions:

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What is the common ordinate of temple and Zoo?

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
What is the common ordinate of temple and Zoo?
a)
5
b)
-2
c)
-3
d)
3

|
Manisha Dhakad answered |
Deepak drove in which quadrants
If x is a positive real number and x2 = 2, then x3 =- a)√2
- b)3√2
- c)2√2
- d)4
Correct answer is option 'C'. Can you explain this answer?
If x is a positive real number and x2 = 2, then x3 =
a)
√2
b)
3√2
c)
2√2
d)
4
|
|
Neeharika Shah answered |
Explanation:
Given:
x2 = 2
Find:
x3
Solution:
Step 1:
Given x2 = 2, we need to find x3.
Step 2:
To find x3, we can simply multiply x2 by x:
x3 = x * x2
Step 3:
Substitute the value of x2 from the given information:
x3 = x * 2
Step 4:
Since x2 = 2, we can rewrite the above equation as:
x3 = x * √2
Step 5:
Therefore, x3 = 2√2
Conclusion:
Therefore, if x is a positive real number and x2 = 2, then x3 = 2√2. Hence, the correct answer is option 'C'.
Given:
x2 = 2
Find:
x3
Solution:
Step 1:
Given x2 = 2, we need to find x3.
Step 2:
To find x3, we can simply multiply x2 by x:
x3 = x * x2
Step 3:
Substitute the value of x2 from the given information:
x3 = x * 2
Step 4:
Since x2 = 2, we can rewrite the above equation as:
x3 = x * √2
Step 5:
Therefore, x3 = 2√2
Conclusion:
Therefore, if x is a positive real number and x2 = 2, then x3 = 2√2. Hence, the correct answer is option 'C'.
In the adjoining figure, if QP ║ RT, then x is equal to –
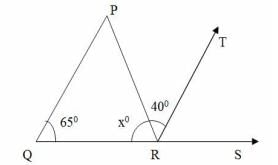
- a)55°
- b)75°
- c)65°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, if QP ║ RT, then x is equal to –


a)
55°
b)
75°
c)
65°
d)
70°
|
|
Aditi Sharma answered |
∠QPR = ∠PRT = 40° (Alternate interior angles)
In ∠QPR, ∠PQR + ∠QPR + ∠PRQ = 180° (Angle sum property)
65° + 40° + x° = 180°
x° = 180° - 40° - 65°
x° = 75
In ∠QPR, ∠PQR + ∠QPR + ∠PRQ = 180° (Angle sum property)
65° + 40° + x° = 180°
x° = 180° - 40° - 65°
x° = 75
A linear equation in two variables is of the form ax + by + c = 0, where- a)a ≠ 0 and b = 0
- b)a = 0 and b = 0
- c)a ≠ 0 and b ≠ 0
- d)a = 0 and b ≠ 0
Correct answer is option 'C'. Can you explain this answer?
A linear equation in two variables is of the form ax + by + c = 0, where
a)
a ≠ 0 and b = 0
b)
a = 0 and b = 0
c)
a ≠ 0 and b ≠ 0
d)
a = 0 and b ≠ 0
|
|
Swati Verma answered |
A linear equation in two variables is of the form ax + by + c = 0 as a and b are cofficient of x and y
so if a = 0 and b = 0 or either of one is zero in that case the equation will be one variable or their will be no equation respectively.
therefore when a ≠ 0 and b ≠ 0 then only the equation will be in two variable
so if a = 0 and b = 0 or either of one is zero in that case the equation will be one variable or their will be no equation respectively.
therefore when a ≠ 0 and b ≠ 0 then only the equation will be in two variable
The area of a triangle with base 8 cm and height 10 cm is- a)80 cm2
- b)18 cm2
- c)40 cm2
- d)20 cm2
Correct answer is option 'C'. Can you explain this answer?
The area of a triangle with base 8 cm and height 10 cm is
a)
80 cm2
b)
18 cm2
c)
40 cm2
d)
20 cm2
|
|
Pooja Shah answered |
Area = 1/2 x Base x Height
= 1/2 x 8 x 10
= 40 cm2
= 1/2 x 8 x 10
= 40 cm2
Read the text carefully and answer the questions:
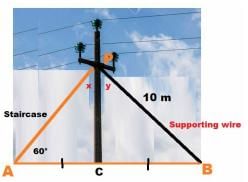
As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
The value of ∠x is- a)30°
- b)60°
- c)90°
- d)45°
Correct answer is option 'A'. Can you explain this answer?
Read the text carefully and answer the questions:

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
The value of ∠x is

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
The value of ∠x is
a)
30°
b)
60°
c)
90°
d)
45°
|
|
Amit Kumar answered |
30°
Read the text carefully and answer the questions:
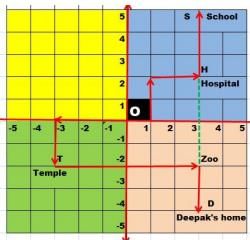
In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
Sanjay Drove in which quadrants?- a)I only
- b)II and I
- c)III and IV
- d)II and III
Correct answer is option 'A'. Can you explain this answer?
Read the text carefully and answer the questions:

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
Sanjay Drove in which quadrants?

In the above picture, one small square is of size 1 km 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
Sanjay Drove in which quadrants?
a)
I only
b)
II and I
c)
III and IV
d)
II and III
|
|
Swati Verma answered |
I only
Read the text carefully and answer the questions:

Roshan decorated one of his bathroom wall with tiles as shown in the picture. He was having tiles of four colours orange, yellow, green and blue. He fitted the tiles in 8 columns and 12 rows. The size of one tile was 1 foot x 1 foot and the area of each tile is 1 foot².
He arranged the tile in such a way that colour of tiles in each row and column were in the pattern:
Orange-> Yellow-> green->Blue->Orange->..... and so on.
Which colour tile was fitted at the point with coordinates (7, 7)?- a)Orange
- b)Green
- c)Yellow
- d)Blue
Correct answer is option 'A'. Can you explain this answer?
Read the text carefully and answer the questions:

Roshan decorated one of his bathroom wall with tiles as shown in the picture. He was having tiles of four colours orange, yellow, green and blue. He fitted the tiles in 8 columns and 12 rows. The size of one tile was 1 foot x 1 foot and the area of each tile is 1 foot².
He arranged the tile in such a way that colour of tiles in each row and column were in the pattern:
Orange-> Yellow-> green->Blue->Orange->..... and so on.
Which colour tile was fitted at the point with coordinates (7, 7)?

Roshan decorated one of his bathroom wall with tiles as shown in the picture. He was having tiles of four colours orange, yellow, green and blue. He fitted the tiles in 8 columns and 12 rows. The size of one tile was 1 foot x 1 foot and the area of each tile is 1 foot².
He arranged the tile in such a way that colour of tiles in each row and column were in the pattern:
Orange-> Yellow-> green->Blue->Orange->..... and so on.
Which colour tile was fitted at the point with coordinates (7, 7)?
a)
Orange
b)
Green
c)
Yellow
d)
Blue
|
|
Vikas Kapoor answered |
Orange
The sides of a triangle are in ratio 3 : 4 : 5. If the perimeter of the triangle is 84 cm, then area of the triangle is :- a)274 cm2
- b)252 cm2
- c)294 cm2
- d)290 cm2
Correct answer is option 'C'. Can you explain this answer?
The sides of a triangle are in ratio 3 : 4 : 5. If the perimeter of the triangle is 84 cm, then area of the triangle is :
a)
274 cm2
b)
252 cm2
c)
294 cm2
d)
290 cm2
|
|
Meera Rana answered |
Let the sides be 3x, 4x and 5x.
Then according to quesiton, 3x + 4x + 5x = 84
⇒ 12x = 84
⇒ x = 7
Therefore, the sides are 3 x 7 = 21, cm, 4 x 7 = 28 cm and 5 x 7 = 35 cm
s =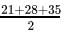 = 42 cm
= 42 cm
Area of triangle =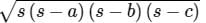
=
=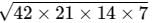
= 21 7 2 = 294 sq. cm
Then according to quesiton, 3x + 4x + 5x = 84
⇒ 12x = 84
⇒ x = 7
Therefore, the sides are 3 x 7 = 21, cm, 4 x 7 = 28 cm and 5 x 7 = 35 cm
s =
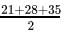 = 42 cm
= 42 cmArea of triangle =
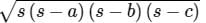
=

=
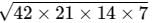
= 21 7 2 = 294 sq. cm
Read the text carefully and answer the questions:
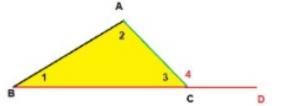
Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the first angle?- a)60°
- b)90°
- c)30°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
Read the text carefully and answer the questions:

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the first angle?

Ashok is studying in 9th class in Govt School, Chhatarpur. Once he was at his home and was doing his geometry homework.
He was trying to measure three angles of a triangle using the Dee, but his dee was old and his Dee's numbers were erased and the lines on the dee were visible.
Let us help Ashok to find the angles of the triangle.
He found that the second angle of the triangle was three times as large as the first. The measure of the third angle is double of the first angle.
What was the value of the first angle?
a)
60°
b)
90°
c)
30°
d)
45°
|
|
Aditi Sharma answered |
30°
Read the text carefully and answer the questions:
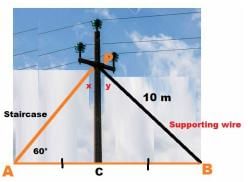
As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the figure, ΔPAC and ΔPBC are congruent due to which criteria?- a)ASA
- b)SSS
- c)SAS
- d)RHS
Correct answer is option 'D'. Can you explain this answer?
Read the text carefully and answer the questions:

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the figure, ΔPAC and ΔPBC are congruent due to which criteria?

As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
In the figure, ΔPAC and ΔPBC are congruent due to which criteria?
a)
ASA
b)
SSS
c)
SAS
d)
RHS
|
|
Swati Verma answered |
RHS
The point (a, -a) does not lie on the graph of- a)y = x
- b)x + y = 0
- c)x = a
- d)y = -a
Correct answer is option 'A'. Can you explain this answer?
The point (a, -a) does not lie on the graph of
a)
y = x
b)
x + y = 0
c)
x = a
d)
y = -a
|
|
Nitya Tiwari answered |
Explanation:
To determine whether the point (a, -a) lies on the graph of a given equation, we substitute the values of x and y from the point into the equation and check if the equation holds true.
a) y = x:
When we substitute x = a and y = -a into the equation y = x, we get:
- a = a
This equation is true, which means the point (a, -a) lies on the graph of y = x.
b) xy = 0:
When we substitute x = a and y = -a into the equation xy = 0, we get:
- a * (-a) = 0
a^2 = 0
This equation is not true unless a = 0. Therefore, the point (a, -a) does not lie on the graph of xy = 0.
c) x = a:
When we substitute x = a and y = -a into the equation x = a, we get:
a = a
This equation is true, which means the point (a, -a) lies on the graph of x = a.
d) y = -a:
When we substitute x = a and y = -a into the equation y = -a, we get:
- a = -a
This equation is true, which means the point (a, -a) lies on the graph of y = -a.
Conclusion:
From the analysis above, we can see that the point (a, -a) does not lie on the graph of xy = 0, so the correct answer is option A.
To determine whether the point (a, -a) lies on the graph of a given equation, we substitute the values of x and y from the point into the equation and check if the equation holds true.
a) y = x:
When we substitute x = a and y = -a into the equation y = x, we get:
- a = a
This equation is true, which means the point (a, -a) lies on the graph of y = x.
b) xy = 0:
When we substitute x = a and y = -a into the equation xy = 0, we get:
- a * (-a) = 0
a^2 = 0
This equation is not true unless a = 0. Therefore, the point (a, -a) does not lie on the graph of xy = 0.
c) x = a:
When we substitute x = a and y = -a into the equation x = a, we get:
a = a
This equation is true, which means the point (a, -a) lies on the graph of x = a.
d) y = -a:
When we substitute x = a and y = -a into the equation y = -a, we get:
- a = -a
This equation is true, which means the point (a, -a) lies on the graph of y = -a.
Conclusion:
From the analysis above, we can see that the point (a, -a) does not lie on the graph of xy = 0, so the correct answer is option A.
An isosceles right triangle has area 8cm2. The length of its hypotenuse is - a)√24 cm
- b)√48 cm
- c)√16 cm
- d)√32 cm
Correct answer is option 'D'. Can you explain this answer?
An isosceles right triangle has area 8cm2. The length of its hypotenuse is
a)
√24 cm
b)
√48 cm
c)
√16 cm
d)
√32 cm
|
|
Swati Verma answered |
Area of isosceles right triangle = 8 sq. cm
1/2 x Base Base = 8 [Since in isosceles right triangle, base and perpendicular are same]
⇒ (Base)2 = 16
⇒ Base = 4 cm
Hypotenuse =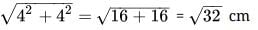
1/2 x Base Base = 8 [Since in isosceles right triangle, base and perpendicular are same]
⇒ (Base)2 = 16
⇒ Base = 4 cm
Hypotenuse =
If x < 0 and y < 0, then the point (x, y) lies in- a)I Quadrant
- b)II Quadrant
- c)III Quadrant
- d)IV Quadrant
Correct answer is option 'C'. Can you explain this answer?
If x < 0 and y < 0, then the point (x, y) lies in
a)
I Quadrant
b)
II Quadrant
c)
III Quadrant
d)
IV Quadrant
|
|
Swati Verma answered |
Here,x < 0 (i.e, -ve) and y < 0, (i.e, -ve)
And we know that,co-ordinate of the point in 3rd quadrant is (-,-)i.e, both negative,
So,the given point will lie in 3rd quadrant.
And we know that,co-ordinate of the point in 3rd quadrant is (-,-)i.e, both negative,
So,the given point will lie in 3rd quadrant.
Choose the wrong statement:- a)Every integer is a rational number.
- b)Every rational number is a real number
- c)Every rational number is an integer.
- d)Every natural number is a whole number.
Correct answer is option 'C'. Can you explain this answer?
Choose the wrong statement:
a)
Every integer is a rational number.
b)
Every rational number is a real number
c)
Every rational number is an integer.
d)
Every natural number is a whole number.
|
|
Swati Verma answered |
Every rational number is an integer.
Eg. 1/2 is a rational number but not an integer.
Eg. 1/2 is a rational number but not an integer.
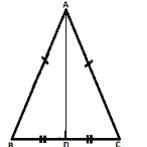
In the adjoining figure, AB = AC and AD is median of ΔABC , then ∠ADC is equal to
- a)90o
- b)60o
- c)75o
- d)120o
Correct answer is option 'A'. Can you explain this answer?
In the adjoining figure, AB = AC and AD is median of ΔABC , then ∠ADC is equal to


a)
90o
b)
60o
c)
75o
d)
120o
|
|
Aditi Sharma answered |
As AD is the perpendicular bisector of BC, so ∠ADC = ∠ADB = 90o
Chapter doubts & questions for Sample Papers with Solutions - Mathematics (Maths) Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sample Papers with Solutions - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|471 docs|57 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

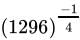 =
=