All questions of Percentages for Mechanical Engineering Exam
Weight of A and B are in the ratio of 3:5. If the weight of A is increased by 20 percent and then the total weight becomes 132 kg with an increase of 10 percent. B weight is increased by what percent.- a)2%
- b)3%
- c)4%
- d)5%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Weight of A and B are in the ratio of 3:5. If the weight of A is increased by 20 percent and then the total weight becomes 132 kg with an increase of 10 percent. B weight is increased by what percent.
a)
2%
b)
3%
c)
4%
d)
5%
e)
None of these

|
Target Study Academy answered |
Answer – 3. 4% Explanation : Weight of A and B are 3x and 5x.
Initial weight before increase = (132*100)/110 = 120 8x = 120. X = 15 Initial weight of A and B are 45 and 75 kg respectively.
New weight of A = 54 so weight of B = 132 – 54 = 78.
So % increase = [(78-75)/75]*100 = 4 %
Initial weight before increase = (132*100)/110 = 120 8x = 120. X = 15 Initial weight of A and B are 45 and 75 kg respectively.
New weight of A = 54 so weight of B = 132 – 54 = 78.
So % increase = [(78-75)/75]*100 = 4 %
A vendor sells 50 percent of apples he had and throws away 20 percent of the remainder. Next day he sells 60 percent of the remainder and throws away the rest. What percent of his apples does the vendor throw?
- a)20%
- b)22%
- c)24%
- d)26%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A vendor sells 50 percent of apples he had and throws away 20 percent of the remainder. Next day he sells 60 percent of the remainder and throws away the rest. What percent of his apples does the vendor throw?
a)
20%
b)
22%
c)
24%
d)
26%
e)
None of these

|
Machine Experts answered |
Let the total number of apples the vendor initially had be 100 (for simplicity).
On the first day:
The vendor sells 50% of the apples:
Apples sold on day 1 = 50% of 100 = 50
The remaining apples after selling 50% are:
Remaining apples = 100 − 50 = 50
He then throws away 20% of the remaining apples:
Apples thrown away on day 1 = 20% of 50 = 10
The remaining apples after throwing away 20% are:
Remaining apples after day 1 = 50 − 10 = 40
On the second day:
The vendor sells 60% of the remaining apples:
Apples sold on day 2 = 60% of 40 = 24
The remaining apples after selling 60% are:
Remaining apples after selling on day 2 = 40 − 24 = 16
He throws away the rest, which is 16 apples.
Total apples thrown away:
Apples thrown away on day 1 = 10
Apples thrown away on day 2 = 16
Total apples thrown away = 10 + 16 = 26
Percentage of apples thrown away:
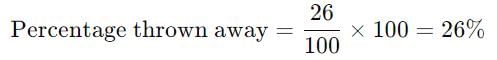
Thus, the vendor throws away 26% of his apples.
On the first day:
The vendor sells 50% of the apples:
Apples sold on day 1 = 50% of 100 = 50
The remaining apples after selling 50% are:
Remaining apples = 100 − 50 = 50
He then throws away 20% of the remaining apples:
Apples thrown away on day 1 = 20% of 50 = 10
The remaining apples after throwing away 20% are:
Remaining apples after day 1 = 50 − 10 = 40
On the second day:
The vendor sells 60% of the remaining apples:
Apples sold on day 2 = 60% of 40 = 24
The remaining apples after selling 60% are:
Remaining apples after selling on day 2 = 40 − 24 = 16
He throws away the rest, which is 16 apples.
Total apples thrown away:
Apples thrown away on day 1 = 10
Apples thrown away on day 2 = 16
Total apples thrown away = 10 + 16 = 26
Percentage of apples thrown away:
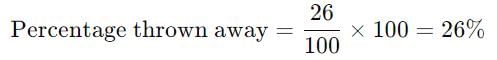
Thus, the vendor throws away 26% of his apples.
In a library, 30% of the books are in History. 50% of the remaining are in English and 40% of the remaining are in German. The remaining 4200 books are in regional languages. What is the total number of books in library?- a)10000
- b)15000
- c)20000
- d)25000
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a library, 30% of the books are in History. 50% of the remaining are in English and 40% of the remaining are in German. The remaining 4200 books are in regional languages. What is the total number of books in library?
a)
10000
b)
15000
c)
20000
d)
25000
e)
None of these

|
Machine Experts answered |
Let the total number of books in the library be T.
30% of the books are in History:
History books = 30% of T = 0.30 × T
The remaining books after accounting for History are:
Remaining books = T − 0.30 × T = 0.70 × T
50% of the remaining books are in English:
English books = 50% of the remaining = 0.50 × 0.70 × T = 0.35 × T
After accounting for English books, the remaining books are:
Remaining books after English = 0.70T − 0.35T = 0.35T
40% of the remaining books are in German:
German books = 40% of the remaining = 0.40 × 0.35 × T = 0.14 × T
After accounting for German books, the remaining books are:
Remaining books after German = 0.35T − 0.14T = 0.21T
The remaining 4200 books are in regional languages, so:
0.21 × T = 4200
Solving for T:
T = 4200/0.21 = 20000
Thus, the total number of books in the library is 20,000.
30% of the books are in History:
History books = 30% of T = 0.30 × T
The remaining books after accounting for History are:
Remaining books = T − 0.30 × T = 0.70 × T
50% of the remaining books are in English:
English books = 50% of the remaining = 0.50 × 0.70 × T = 0.35 × T
After accounting for English books, the remaining books are:
Remaining books after English = 0.70T − 0.35T = 0.35T
40% of the remaining books are in German:
German books = 40% of the remaining = 0.40 × 0.35 × T = 0.14 × T
After accounting for German books, the remaining books are:
Remaining books after German = 0.35T − 0.14T = 0.21T
The remaining 4200 books are in regional languages, so:
0.21 × T = 4200
Solving for T:
T = 4200/0.21 = 20000
Thus, the total number of books in the library is 20,000.
1000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 10% of total students. Then the number of sweets, each student gets.- a)10
- b)12
- c)14
- d)16
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
1000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 10% of total students. Then the number of sweets, each student gets.
a)
10
b)
12
c)
14
d)
16
e)
None of these
|
|
Rajeev Kumar answered |
Answer – a) 10 Explanation : No of students = T. Each student gets 10% of T. So, T students get T^2/10 sweets.
T^2/10 = 1000. We get T =10
T^2/10 = 1000. We get T =10
When the price of rice is increased by 25 percent, a family reduces its consumption such that the expenditure is only 10 percent more than before. If 40 kg of rice is consumed by family before, then find the new consumption of family.- a)34.2
- b)35.2
- c)36.2
- d)37.2
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When the price of rice is increased by 25 percent, a family reduces its consumption such that the expenditure is only 10 percent more than before. If 40 kg of rice is consumed by family before, then find the new consumption of family.
a)
34.2
b)
35.2
c)
36.2
d)
37.2
e)
None of these
|
|
Rhea Reddy answered |
Answer – 2.35.2 Explanation : Suppose initially price per kg of rice is 100 then their expenditure is 4000.
Now their expenditure is only increased by only 10% i.e – 4400.
Increased price of rice = 125.
So new consumption = 4400/125 = 35.2
Now their expenditure is only increased by only 10% i.e – 4400.
Increased price of rice = 125.
So new consumption = 4400/125 = 35.2
40% of the women are above 30 years of age and 80 percent of the women are less than or equal to 50 years of age. 20 percent of all women play basketball.If 30 percent of the women above the age of 50 plays basketball, what percent of players are less than or equal to 50 years?- a)50%
- b)60%
- c)70%
- d)80%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
40% of the women are above 30 years of age and 80 percent of the women are less than or equal to 50 years of age. 20 percent of all women play basketball.If 30 percent of the women above the age of 50 plays basketball, what percent of players are less than or equal to 50 years?
a)
50%
b)
60%
c)
70%
d)
80%
e)
None of these

|
Machine Experts answered |
Let the total number of women be 100 (for simplicity).
Women above 30 years of age:
40% of the women are above 30 years of age, which means:
Women above 30 years = 40% of 100 = 40 women
Women less than or equal to 50 years of age:
80% of the women are less than or equal to 50 years of age, which means:
Women less than or equal to 50 years = 80% of 100 = 80 women
Women above 50 years of age:
Since 80% are less than or equal to 50 years, the remaining 20% are above 50 years of age, which means:
Women above 50 years = 20% of 100 = 20 women
Women who play basketball:
20% of all women play basketball, which means:
Total basketball players = 20% of 100 = 20 women
Women above 50 years of age who play basketball:
30% of the women above 50 years play basketball, which means:
Basketball players above 50 years = 30% of 20 = 6 women
Women less than or equal to 50 years who play basketball:
The total number of basketball players is 20, and 6 of them are above 50 years of age.
Therefore, the number of players less than or equal to 50 years of age is:
Basketball players less than or equal to 50 years = 20 − 6 = 14 women
Percentage of players who are less than or equal to 50 years of age:
Percentage of players less than or equal to 50 years =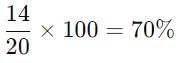
Thus, 70% of the basketball players are less than or equal to 50 years of age.
Women above 30 years of age:
40% of the women are above 30 years of age, which means:
Women above 30 years = 40% of 100 = 40 women
Women less than or equal to 50 years of age:
80% of the women are less than or equal to 50 years of age, which means:
Women less than or equal to 50 years = 80% of 100 = 80 women
Women above 50 years of age:
Since 80% are less than or equal to 50 years, the remaining 20% are above 50 years of age, which means:
Women above 50 years = 20% of 100 = 20 women
Women who play basketball:
20% of all women play basketball, which means:
Total basketball players = 20% of 100 = 20 women
Women above 50 years of age who play basketball:
30% of the women above 50 years play basketball, which means:
Basketball players above 50 years = 30% of 20 = 6 women
Women less than or equal to 50 years who play basketball:
The total number of basketball players is 20, and 6 of them are above 50 years of age.
Therefore, the number of players less than or equal to 50 years of age is:
Basketball players less than or equal to 50 years = 20 − 6 = 14 women
Percentage of players who are less than or equal to 50 years of age:
Percentage of players less than or equal to 50 years =
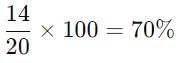
Thus, 70% of the basketball players are less than or equal to 50 years of age.
60 percent of the employees of a company are women and 75% of the women earn 20000 or more in a month. Total number of employees who earns more than 20000 per month in the company is 60 percent of the total employees.What fraction of men earns less than 20000 per month?- a)5/8
- b)5/7
- c)1/5
- d)3/4
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
60 percent of the employees of a company are women and 75% of the women earn 20000 or more in a month. Total number of employees who earns more than 20000 per month in the company is 60 percent of the total employees.What fraction of men earns less than 20000 per month?
a)
5/8
b)
5/7
c)
1/5
d)
3/4
e)
None of these

|
Machine Experts answered |
Total employees = 100 (for simplicity).
Number of women = 60% of 100 = 60 women.
Number of men = 40% of 100 = 40 men.
75% of the women earn 20,000 or more:
Women earning 20,000 or more = 75% of 60 = 0.75 × 60 = 45 women.
Total number of employees earning more than 20,000 per month is 60% of the total employees:
Employees earning more than 20,000 = 60% of 100 = 60 employees.
Out of these 60 employees, 45 are women, so the remaining 15 must be men:
Men earning more than 20,000 = 15 men.
The total number of men is 40, and 15 men earn more than 20,000, so the number of men earning less than 20,000 is:
Men earning less than 20,000 = 40 − 15 = 25 men.
The fraction of men earning less than 20,000 is:
Fraction = 25/40 = 5 / 8
Thus, the correct answer is A: 5/8
Number of women = 60% of 100 = 60 women.
Number of men = 40% of 100 = 40 men.
75% of the women earn 20,000 or more:
Women earning 20,000 or more = 75% of 60 = 0.75 × 60 = 45 women.
Total number of employees earning more than 20,000 per month is 60% of the total employees:
Employees earning more than 20,000 = 60% of 100 = 60 employees.
Out of these 60 employees, 45 are women, so the remaining 15 must be men:
Men earning more than 20,000 = 15 men.
The total number of men is 40, and 15 men earn more than 20,000, so the number of men earning less than 20,000 is:
Men earning less than 20,000 = 40 − 15 = 25 men.
The fraction of men earning less than 20,000 is:
Fraction = 25/40 = 5 / 8
Thus, the correct answer is A: 5/8
In an election contested by two parties A and B, party A secured 25 percent of the total votes more than Party B. If party B gets 15000 votes. By how much votes does party B loses the election?- a)8000
- b)10000
- c)12000
- d)15000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
In an election contested by two parties A and B, party A secured 25 percent of the total votes more than Party B. If party B gets 15000 votes. By how much votes does party B loses the election?
a)
8000
b)
10000
c)
12000
d)
15000
e)
None of these

|
KS Coaching Center answered |
Answer – b) 10000 Explanation : Let total votes = T and party B gets 15000 votes then party A will get T -15000 votes T – 15000 – 15000 = 25T/100
T = 40000, so A get 25000 and B gets 15000 votes, so difference = 10000
T = 40000, so A get 25000 and B gets 15000 votes, so difference = 10000
Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?- a)54.60
- b)55.60
- c)56.60
- d)57.60
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?
a)
54.60
b)
55.60
c)
56.60
d)
57.60
e)
None of these

|
Machine Experts answered |
Total cost of items = ₹60.
Sales tax paid = 40 paise = ₹0.40.
Tax rate = 10%. So, the tax amount is 10% of the cost of taxed items (denoted as T).
The sales tax equation is:

Solving for T:


Solving for T:

Now, the cost of tax-free items is:
Cost of tax-free items = 60 − T − Sales tax = 60 − 4 − 0.40 = 55.60 rupees.
Thus, the cost of tax-free items is ₹55.60.
Cost of tax-free items = 60 − T − Sales tax = 60 − 4 − 0.40 = 55.60 rupees.
Thus, the cost of tax-free items is ₹55.60.
A man has 4000 rupees in his account two years ago. In the first year he deposited 20 percent of the amount in his account. In the next year he deposited 10 percent of the increased amount in the account. Find the total amount in the account of the person after 2 years.- a)6650
- b)5280
- c)5740
- d)5840
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A man has 4000 rupees in his account two years ago. In the first year he deposited 20 percent of the amount in his account. In the next year he deposited 10 percent of the increased amount in the account. Find the total amount in the account of the person after 2 years.
a)
6650
b)
5280
c)
5740
d)
5840
e)
None of these
|
|
Anaya Patel answered |
Answer – b) 5280 Explanation : 4000 + 800 + 480 = 5280
A number is first decreased by 25%. The decreased number is then increased by 20%. The resulting number is less than the original number by 40. Then the original number is –
- a)100
- b)200
- c)300
- d)400
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A number is first decreased by 25%. The decreased number is then increased by 20%. The resulting number is less than the original number by 40. Then the original number is –
a)
100
b)
200
c)
300
d)
400
e)
None of these

|
Cstoppers Instructors answered |
Let the number is a a – (75/100)*a*(120/100) = 40 we will get a = 400
A salary is 40 percent more than B. B’s salary is 30 percent less than C. If the difference between the salary of C and A is 1200 rupees, then what is the monthly income of C - a)50000
- b)60000
- c)70000
- d)80000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A salary is 40 percent more than B. B’s salary is 30 percent less than C. If the difference between the salary of C and A is 1200 rupees, then what is the monthly income of C
a)
50000
b)
60000
c)
70000
d)
80000
e)
None of these
|
|
Kavya Saxena answered |
Answer – 2.60000 Explanation : A = (140/100)*B
B = (70/100)*C
[(100/70) – (140/100)]*B = 1200.
B = 42000.
C = (100/70)*42000 = 60000
B = (70/100)*C
[(100/70) – (140/100)]*B = 1200.
B = 42000.
C = (100/70)*42000 = 60000
A student has to get 40 percent marks to pass an examination. He got 60 marks but fails by 20 marks. Find the maximum marks of the examination.- a)150
- b)200
- c)300
- d)400
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A student has to get 40 percent marks to pass an examination. He got 60 marks but fails by 20 marks. Find the maximum marks of the examination.
a)
150
b)
200
c)
300
d)
400
e)
None of these
|
|
Ravi Singh answered |
Answer –b) 200 Explanation : (40/100)*M – 20 = 60 (M is the maximum marks)
In a library 5 percent books are in English, 10 percent of the remaining are in hindi and 15 percent of the remaining are in Sanskrit. The remaining 11628 books are in French. Then find the total number of books in the library.
- a)8000
- b)12000
- c)16000
- d)20000
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a library 5 percent books are in English, 10 percent of the remaining are in hindi and 15 percent of the remaining are in Sanskrit. The remaining 11628 books are in French. Then find the total number of books in the library.
a)
8000
b)
12000
c)
16000
d)
20000
e)
None of these
|
|
Ravi Singh answered |
5% of books are in English,
10% of remaining books are in Hindi,
15% of remaining books are in Sanskrit.
Remaining books are in french = 11628
Calculation:
Let the total books in the library be 100%
According to question:
5% of books are in English
Remaining books = 100 - 5 = 95%
10% of remaining are in hindi = 10% of 95 = 9.5
Remaining books = 95 - 9.5 = 85.5%
15% of remaining books are in sanskrit = 15% of 85.5 = 12.825%
Remaining books = 85% - 12.825% = 72.675%
According to question:
72.675% = 11628
⇒ 1% = (11628/72.675)
⇒ 100% = (11628/72.675)× 100 = 16000
∴ Required value = 16000
When the price of rice is increased by 30 percent, a family reduces its consumption such that the expenditure is only 20 percent more than before. If 50 kg of rice is consumed by family before, then find the new consumption of family (approx.)- a)43kg
- b)44kg
- c)45kg
- d)46kg
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
When the price of rice is increased by 30 percent, a family reduces its consumption such that the expenditure is only 20 percent more than before. If 50 kg of rice is consumed by family before, then find the new consumption of family (approx.)
a)
43kg
b)
44kg
c)
45kg
d)
46kg
e)
None of these

|
Cstoppers Instructors answered |
Answer – 4.46kg Explanation : Suppose initially price per kg of rice is 100 then their expenditure is 5000.
Now their expenditure is only increased by only 20% i.e – 6000.
Increased price of rice = 130.
So new consumption = 6000/130 = 46.1
Now their expenditure is only increased by only 20% i.e – 6000.
Increased price of rice = 130.
So new consumption = 6000/130 = 46.1
Pankaj gave 50 percent of the amount to akash. Akash in turn gave two-fifth of the amount to venu. After paying a bill of 500 rupees, venu now have 8000 rupees left with him. Find the amount hold by pankaj initially.- a)41500
- b)42500
- c)43500
- d)44500
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Pankaj gave 50 percent of the amount to akash. Akash in turn gave two-fifth of the amount to venu. After paying a bill of 500 rupees, venu now have 8000 rupees left with him. Find the amount hold by pankaj initially.
a)
41500
b)
42500
c)
43500
d)
44500
e)
None of these

|
Cstoppers Instructors answered |
Answer – 2. 42500 Explanation : Let pankaj have P amount initially [[(50/100)*P]*2/5 – 500] = 8000
P = 42500
P = 42500
If the price of an article is increased by 15%, then by how much the household should decrease their consumption so as to keep his expenditure same.- a)13(1/23)%
- b)13(2/23)%
- c)11(1/23)%
- d)11(2/23)%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the price of an article is increased by 15%, then by how much the household should decrease their consumption so as to keep his expenditure same.
a)
13(1/23)%
b)
13(2/23)%
c)
11(1/23)%
d)
11(2/23)%
e)
None of these
|
|
Yash Patel answered |
Answer – 1.13(1/23)% Explanation : Decrease in expenditure = (15/115)*100 = 300/23 %
The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?- a)10000
- b)12500
- c)15000
- d)17500
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?
a)
10000
b)
12500
c)
15000
d)
17500
e)
None of these

|
Divey Sethi answered |
We can use the formula for compound growth to find the initial population:


where:
- P is the final population (21600)
- P0 is the initial population (what we want to find)
- r is the annual growth rate (20% or 0.20)
- n is the number of years (3)
Plug in the known values:
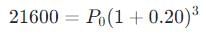
Simplify and solve for P0:
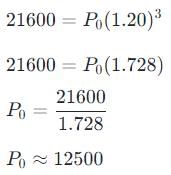
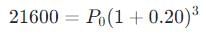
Simplify and solve for P0:
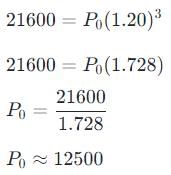
The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?- a)10000
- b)12500
- c)15000
- d)17500
Correct answer is option 'B'. Can you explain this answer?
The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?
a)
10000
b)
12500
c)
15000
d)
17500

|
Bayshore Academy answered |
- The population increases by 20% annually, meaning it multiplies by 1.20 each year.
- After 3 years, the population is 21600.
- Using the compound growth formula P=P0(1+r)t, where P = 21600, r = 0.20, and t = 3, we calculate the initial population P0.
- Solving 21600=P0 x (1.20)3, we find P0 = 12500.
- The initial population is therefore 12500.
30 litre of solution contains alcohol and water in the ratio 2:3. How much alcohol must be added to the solution to make a solution containing 60% of alcohol?- a)10
- b)12
- c)14
- d)15
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
30 litre of solution contains alcohol and water in the ratio 2:3. How much alcohol must be added to the solution to make a solution containing 60% of alcohol?
a)
10
b)
12
c)
14
d)
15
e)
None of these

|
Machine Experts answered |
The initial solution contains 30 liters, with alcohol and water in the ratio 2:3.
The amount of alcohol in the solution is:
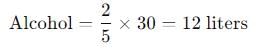
The amount of water in the solution is:
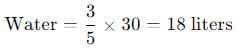
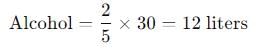
The amount of water in the solution is:
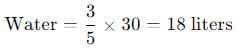
We need to add some amount of alcohol (let it be x) to make the alcohol content 60% of the total solution.
After adding x liters of alcohol, the new total volume of the solution will be 30 + x liters, and the amount of alcohol will be 12 + x liters.
The concentration of alcohol should be 60%, so:
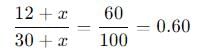
Solving the equation:
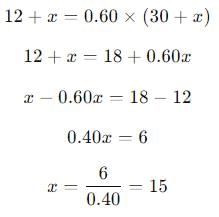
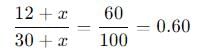
Solving the equation:
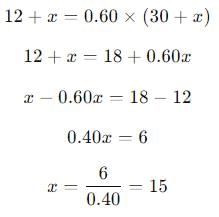
Thus, 15 liters of alcohol must be added to the solution.
If the price of an article is increased by 15%, then by how much the household should decrease their consumption so as to keep his expenditure same.- a)13(1/23) %
- b)13(2/23)%
- c)11(1/23)%
- d)11(2/23)%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the price of an article is increased by 15%, then by how much the household should decrease their consumption so as to keep his expenditure same.
a)
13(1/23) %
b)
13(2/23)%
c)
11(1/23)%
d)
11(2/23)%
e)
None of these
|
|
Nikita Singh answered |
Answer – a) 13(1/23) % Explanation : Decrease in expenditure = (15/115)*100 = 300/23 %
A man spends 60% of his income. His income is increased by 20% and his expenditure also increases by 10%. Find the percentage decrease in his saving?- a)10%
- b)15%
- c)20%
- d)25%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A man spends 60% of his income. His income is increased by 20% and his expenditure also increases by 10%. Find the percentage decrease in his saving?
a)
10%
b)
15%
c)
20%
d)
25%
e)
None of these
|
|
Rhea Reddy answered |
Answer – a) 10% Explanation : Let initially income is 100. So, expenditure = 60 and saving = 40 now income is increased by 20% i.e. 120. So, expenditure = (70/100)*120 = 84 and saving = 36 so % percent decrease in saving = (4/40)*100 = 10%
The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?- a)increase 4.32%
- b)decrease 4.32%
- c)increase 3.32 percent
- d)decrease 3.32%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?
a)
increase 4.32%
b)
decrease 4.32%
c)
increase 3.32 percent
d)
decrease 3.32%
e)
None of these

|
Cstoppers Instructors answered |
Answer – b) decrease 4.32% Explanation : Let initially seats are 100 and price of each seat is 100, so total initial revenue = 10000
now, seats are 92 and price of each seat = 104, so total revenue = 92*104 = 9568 so percent change in revenue = (432/10000)*100 = 4.32 decrease
now, seats are 92 and price of each seat = 104, so total revenue = 92*104 = 9568 so percent change in revenue = (432/10000)*100 = 4.32 decrease
Rakesh spent 30 percent of his monthly income on food items. Of the remaining amount he spent 60 percent on clothes and bills. Now he save fiveseventh of the remaining amount and the he saves 120000 yearly, then find his monthly income.- a)40000
- b)50000
- c)60000
- d)70000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Rakesh spent 30 percent of his monthly income on food items. Of the remaining amount he spent 60 percent on clothes and bills. Now he save fiveseventh of the remaining amount and the he saves 120000 yearly, then find his monthly income.
a)
40000
b)
50000
c)
60000
d)
70000
e)
None of these

|
Cstoppers Instructors answered |
Answer – 2. 50000 Explanation : Let monthly income is P (70/100)*P*(40/100)*5/7 = 10000
P = 50000
P = 50000
A got 30% of the maximum marks in an examination and failed by 10 marks. However, B who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?- a)65
- b)75
- c)80
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A got 30% of the maximum marks in an examination and failed by 10 marks. However, B who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
a)
65
b)
75
c)
80
d)
None of these

|
Engineers Adda answered |
(30/100)*T = P -10
(40/100)*T = P + 15
U will get P = 85
(40/100)*T = P + 15
U will get P = 85
Weights of two friends A and B are in the ratio of 1 : 2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?
- a)30%
- b)35%
- c)40%
- d)45%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Weights of two friends A and B are in the ratio of 1 : 2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?
a)
30%
b)
35%
c)
40%
d)
45%
e)
None of these

|
KS Coaching Center answered |
Let the original weights of A and B be A and B, respectively. Since the ratio of their weights is 1 : 2, we can say:
A = x and B = 2x
A’s weight increases by 20%, so the new weight of A is:
New weight of A = A + 20% of A = x + 0.20x = 1.2x
The total weight of A and B after the increase is 60 kg, and it is also given that the total weight increased by 30%. Therefore, the original total weight of A and B was:
Original total weight = 60/1.30 = 46.15 kg (approximately)
The original total weight of A and B is also A + B = x + 2x = 3x, so:
3 x = 46.15 ⇒ x = 46.15/3 = 15.38 kg (approximately)
So, A’s original weight is approximately 15.38 kg, and B’s original weight is:
B = 2x = 2 × 15.38 = 30.76 kg (approximately)
The new total weight is 60 kg, and the new weight of A is 1.2x = 1.2 × 15.38 = 18.46 kg. Therefore, the new weight of B is:
New weight of B = 60 − 18.46 = 41.54 kg (approximately)
Now, we can calculate the percentage increase in B’s weight:
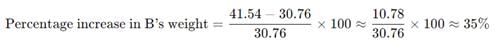
A = x and B = 2x
A’s weight increases by 20%, so the new weight of A is:
New weight of A = A + 20% of A = x + 0.20x = 1.2x
The total weight of A and B after the increase is 60 kg, and it is also given that the total weight increased by 30%. Therefore, the original total weight of A and B was:
Original total weight = 60/1.30 = 46.15 kg (approximately)
The original total weight of A and B is also A + B = x + 2x = 3x, so:
3 x = 46.15 ⇒ x = 46.15/3 = 15.38 kg (approximately)
So, A’s original weight is approximately 15.38 kg, and B’s original weight is:
B = 2x = 2 × 15.38 = 30.76 kg (approximately)
The new total weight is 60 kg, and the new weight of A is 1.2x = 1.2 × 15.38 = 18.46 kg. Therefore, the new weight of B is:
New weight of B = 60 − 18.46 = 41.54 kg (approximately)
Now, we can calculate the percentage increase in B’s weight:
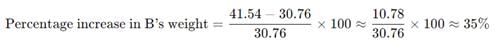
Thus, B’s weight increased by 35%.
The population of a town is 15000. It increases by 10 percent in the first year and 20 percent in the second year. But in the third year it decreases by 10 percent. What will be the population after 3 years.- a)16820
- b)15820
- c)17820
- d)19820
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The population of a town is 15000. It increases by 10 percent in the first year and 20 percent in the second year. But in the third year it decreases by 10 percent. What will be the population after 3 years.
a)
16820
b)
15820
c)
17820
d)
19820
e)
None of these
|
|
Anaya Patel answered |
Answer – c) 17820 Explanation : 15000*(11/10)*(12/10)*(9/10) = 17820
The marked price of an article is 20% higher than the cost price. A discount of 20% is given on the marked price. In this transaction the seller- a)bears no loss no profit
- b)losses 4%
- c)gain 4%
- d)losses 1%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The marked price of an article is 20% higher than the cost price. A discount of 20% is given on the marked price. In this transaction the seller
a)
bears no loss no profit
b)
losses 4%
c)
gain 4%
d)
losses 1%
e)
None of these
|
|
Faizan Khan answered |
Answer – b) losses 4% Explanation : let cost price = 100 so, marked price = 120 now discount of 20% is given, so sp = 120*80/100 = 96 so % loss = (4/100)*100 = 4 percent
In a factory there are three types of bulbs L1, L2 and L3 which produces 20%, 15% and 32% of the total products respectively. L1, L2 and L3 produces 3%, 7% and 2% defective products, respectively. Find the percentage of nondefective products ?- a)46%
- b)30%
- c)53%
- d)64%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
In a factory there are three types of bulbs L1, L2 and L3 which produces 20%, 15% and 32% of the total products respectively. L1, L2 and L3 produces 3%, 7% and 2% defective products, respectively. Find the percentage of nondefective products ?
a)
46%
b)
30%
c)
53%
d)
64%
e)
None of these
|
|
Faizan Khan answered |
Answer – 4.64% Explanation : (20*0.97)+(15*0.93)+(32*0.98) = 19.4+13.95+31.36
= 64.71
= 64.71
The maximum marks per paper in 3 subjects in Mathematics , Physics and Chemistry are set in the ratio 1 : 2 : 3 respectively. Giri obtained 40% in Mathematics, 60% in Physics and 35% in Chemistry papers. What is overall percentage marks did he get overall?- a)44%
- b)32%
- c)50%
- d)60%
Correct answer is option 'A'. Can you explain this answer?
The maximum marks per paper in 3 subjects in Mathematics , Physics and Chemistry are set in the ratio 1 : 2 : 3 respectively. Giri obtained 40% in Mathematics, 60% in Physics and 35% in Chemistry papers. What is overall percentage marks did he get overall?
a)
44%
b)
32%
c)
50%
d)
60%

|
EduRev GATE answered |
40*1/100 : 60*2/100 : 35*3/100 = 0.4:1.2:1.05
Overall % =100* [0.4+1.2+1.05]/1+2+3 = 265/6 = 44.16 = 44%
Overall % =100* [0.4+1.2+1.05]/1+2+3 = 265/6 = 44.16 = 44%
12 percent of the voters in an election did not cast their votes. In this election there are only two candidates. The winner by obtaining 45% of the total votes and defeated his rival by 2000 votes. The total number of votes in the election- a)50000
- b)75000
- c)100000
- d)125000
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
12 percent of the voters in an election did not cast their votes. In this election there are only two candidates. The winner by obtaining 45% of the total votes and defeated his rival by 2000 votes. The total number of votes in the election
a)
50000
b)
75000
c)
100000
d)
125000
e)
None of these

|
Cstoppers Instructors answered |
12% percent didn’t cast their vote. 45% of total votes get by the winning candidates, so remaining 43% will be scored by his rival. So, (45/100 -43/100)*P = 2000
P = 100000
P = 100000
In an examination 70% candidates passed in prelims and 55% candidates passed in Mains. If 62% candidates passed in both these subjects, then what per cent of candidates failed in both the exams?- a)37%
- b)26%
- c)43%
- d)15%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In an examination 70% candidates passed in prelims and 55% candidates passed in Mains. If 62% candidates passed in both these subjects, then what per cent of candidates failed in both the exams?
a)
37%
b)
26%
c)
43%
d)
15%
e)
None of these
|
|
Rajeev Kumar answered |
Answer – 1.37% Explanation : Students passed in Prelims = 70% Students passed in Mains = 55% Students passed in both = 62% No of students passed in at least one subject = (70+55)-62 = 63%. students failed in both subjects = 100-63 = 37%.
2000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 20% of total students. Then the number of sweets, each student gets.
- a)50
- b)20
- c)120
- d)150
Correct answer is option 'B'. Can you explain this answer?
2000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 20% of total students. Then the number of sweets, each student gets.
a)
50
b)
20
c)
120
d)
150

|
Gate Funda answered |
(20/100)*t*t = 2000 (total students = t)
The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?- a)increase 4.32%
- b)decrease 4.32%
- c)increase 3.32 percent
- d)decrease 3.32%
Correct answer is option 'B'. Can you explain this answer?
The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?
a)
increase 4.32%
b)
decrease 4.32%
c)
increase 3.32 percent
d)
decrease 3.32%

|
EduRev GATE answered |
Let initially seats are 100 and price of each seat is 100, so total initial revenue = 10000
now, seats are 92 and price of each seat = 104, so total revenue = 92*104 = 9568
so percent change in revenue = (432/10000)*100 = 4.32 decrease
now, seats are 92 and price of each seat = 104, so total revenue = 92*104 = 9568
so percent change in revenue = (432/10000)*100 = 4.32 decrease
Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?- a)54.60
- b)55.60
- c)56.60
- d)57.60
Correct answer is option 'B'. Can you explain this answer?
Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?
a)
54.60
b)
55.60
c)
56.60
d)
57.60
|
|
Niharika Basu answered |
Calculation of Tax-Free Items Cost:
Explanation:
- Total cost of items = Rs. 60
- Sales tax = 40 paise
- Tax rate = 10%
Step 1: Calculate the total tax amount
- Tax rate = 10%
- Total cost of items = Rs. 60
- Tax amount = 10% of Rs. 60 = Rs. 6
Step 2: Convert the tax amount to paise
- 1 Rupee = 100 paise
- Rs. 6 = 6 * 100 = 600 paise
Step 3: Calculate the tax-free items cost
- Total cost of items = Rs. 60 = 6000 paise
- Sales tax = 40 paise
- Total tax amount = 600 paise
- Cost of tax-free items = Total cost of items - Total tax amount
- Cost of tax-free items = 6000 paise - 600 paise = 5400 paise = Rs. 54
Therefore, the cost of the tax-free items is Rs. 54.60, which is option 'B'.
Explanation:
- Total cost of items = Rs. 60
- Sales tax = 40 paise
- Tax rate = 10%
Step 1: Calculate the total tax amount
- Tax rate = 10%
- Total cost of items = Rs. 60
- Tax amount = 10% of Rs. 60 = Rs. 6
Step 2: Convert the tax amount to paise
- 1 Rupee = 100 paise
- Rs. 6 = 6 * 100 = 600 paise
Step 3: Calculate the tax-free items cost
- Total cost of items = Rs. 60 = 6000 paise
- Sales tax = 40 paise
- Total tax amount = 600 paise
- Cost of tax-free items = Total cost of items - Total tax amount
- Cost of tax-free items = 6000 paise - 600 paise = 5400 paise = Rs. 54
Therefore, the cost of the tax-free items is Rs. 54.60, which is option 'B'.
One type of liquid contains 20 percent milk and in other liquid it contains 30 percent milk. If 4 parts of the first and 6 parts of the second are taken and formed a new liquid A. Find the percentage of milk in third liquid.- a)26
- b)28
- c)29
- d)30
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
One type of liquid contains 20 percent milk and in other liquid it contains 30 percent milk. If 4 parts of the first and 6 parts of the second are taken and formed a new liquid A. Find the percentage of milk in third liquid.
a)
26
b)
28
c)
29
d)
30
e)
None of these
|
|
Aisha Gupta answered |
Answer – a) 26 Explanation : milk = 20 and water = 80 (in 1 liquid) milk = 30 and water = 70 (in 2 liquid) milk in final mixture = 20*4 + 30*6 = 260 so (260/1000)*100 = 26%
The prices of two articles are in the ratio 3 : 4. If the price of the first article be increased by 10% and that of the second by Rs. 4, the original ratio remains the same. The original price of the second article is:- a)Rs.40
- b)Rs.35
- c)Rs.10
- d)Rs.30
Correct answer is option 'A'. Can you explain this answer?
The prices of two articles are in the ratio 3 : 4. If the price of the first article be increased by 10% and that of the second by Rs. 4, the original ratio remains the same. The original price of the second article is:
a)
Rs.40
b)
Rs.35
c)
Rs.10
d)
Rs.30
|
|
Tarun Chawla answered |
Given:
The prices of two articles are in the ratio 3 : 4.
Let:
Let the original price of the first article be 3x and the original price of the second article be 4x.
According to the question:
If the price of the first article is increased by 10%, the new price becomes 3.3x.
If the price of the second article is increased by Rs. 4, the new price becomes 4x + 4.
Given:
The new ratio of the prices is still 3.3 : (4x + 4).
Equating the ratios:
3.3 / (4x + 4) = 3 / 4
Solving the equation:
12.4 = 3(4x + 4)
12.4 = 12x + 12
12.4 - 12 = 12x
0.4 = 12x
x = 0.4 / 12
x = 0.0333
Calculating the original price of the second article:
Original price of the second article = 4x
= 4 * 0.0333
= Rs. 0.1333
Therefore, the original price of the second article is Rs. 40.
The prices of two articles are in the ratio 3 : 4.
Let:
Let the original price of the first article be 3x and the original price of the second article be 4x.
According to the question:
If the price of the first article is increased by 10%, the new price becomes 3.3x.
If the price of the second article is increased by Rs. 4, the new price becomes 4x + 4.
Given:
The new ratio of the prices is still 3.3 : (4x + 4).
Equating the ratios:
3.3 / (4x + 4) = 3 / 4
Solving the equation:
12.4 = 3(4x + 4)
12.4 = 12x + 12
12.4 - 12 = 12x
0.4 = 12x
x = 0.4 / 12
x = 0.0333
Calculating the original price of the second article:
Original price of the second article = 4x
= 4 * 0.0333
= Rs. 0.1333
Therefore, the original price of the second article is Rs. 40.
One type of liquid contains 20 percent of milk and second type of liquid contains 40 percent milk. If 4 part of the first and 6 part of the second are mix, then what is the percent of water in the mixture.- a)64%
- b)66%
- c)68%
- d)70%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
One type of liquid contains 20 percent of milk and second type of liquid contains 40 percent milk. If 4 part of the first and 6 part of the second are mix, then what is the percent of water in the mixture.
a)
64%
b)
66%
c)
68%
d)
70%
e)
None of these
|
|
Alok Verma answered |
Answer – 3.68% Explanation : Do these type of question by taking 100 litre water = 80ltr and 60ltr in first and second mixture respectively now percent of water = [(80*4 + 60*6)/1000]100 = 68%
Sohan spends 23% of an amount of money on an insurance policy, 33% on food, 19% on children’s education and 16% on recreation. He deposits the remaining amount of Rs. 504 in bank. How much total amount did he spend on food and insurance policy together?- a)Rs.3146
- b)Rs.3126
- c)Rs.3136
- d)Rs.3048
Correct answer is option 'C'. Can you explain this answer?
Sohan spends 23% of an amount of money on an insurance policy, 33% on food, 19% on children’s education and 16% on recreation. He deposits the remaining amount of Rs. 504 in bank. How much total amount did he spend on food and insurance policy together?
a)
Rs.3146
b)
Rs.3126
c)
Rs.3136
d)
Rs.3048

|
Gate Funda answered |
Total amount = x
Savings(%)
[100 – (23 + 33 + 19 + 16 )]% = 9 %
9% of x = 504
=> x = 504 * 100/9 = 5600
Amount spend on food and insurance policy together = 56% of 5600 = Rs.3136
Savings(%)
[100 – (23 + 33 + 19 + 16 )]% = 9 %
9% of x = 504
=> x = 504 * 100/9 = 5600
Amount spend on food and insurance policy together = 56% of 5600 = Rs.3136
Fresh fruits contain 75% while dry fruits contain 20% water. If the weight of dry fruits is 300 kg, what was its total weight when it was fresh?- a)900kg
- b)850kg
- c)920kg
- d)960kg
Correct answer is option 'D'. Can you explain this answer?
Fresh fruits contain 75% while dry fruits contain 20% water. If the weight of dry fruits is 300 kg, what was its total weight when it was fresh?
a)
900kg
b)
850kg
c)
920kg
d)
960kg

|
Engineers Adda answered |
Quantity of water in 300 kg dry fruits, = (20 /100) *300 = 60 kg
Quantity of fruit alone= 300-60 =240 kg
25 kg fruit piece in 100 kg fresh fruits
For 240 = (100 *240)/25 = 960 kg.
Quantity of fruit alone= 300-60 =240 kg
25 kg fruit piece in 100 kg fresh fruits
For 240 = (100 *240)/25 = 960 kg.
The total salary of Guagn and Harish in an organization is Rs 30000. If the salary of Gugan increase by 5% and salary of Harish increase by 7%, then their total salary would increase to Rs 31800. Find the salary of Harish ?- a)Rs.10,000
- b)Rs.15,000
- c)Rs.18,000
- d)Rs.12,000
Correct answer is option 'B'. Can you explain this answer?
The total salary of Guagn and Harish in an organization is Rs 30000. If the salary of Gugan increase by 5% and salary of Harish increase by 7%, then their total salary would increase to Rs 31800. Find the salary of Harish ?
a)
Rs.10,000
b)
Rs.15,000
c)
Rs.18,000
d)
Rs.12,000

|
EduRev GATE answered |
7% increases 30000 = Rs 2100 =30000+2100 = Rs 32,100
But the actual increase in salary = 31800
Difference =32100 – 31800 = 300
2% = 300
Gugan’s salary =300/2 x 100 = 15000
Harish’s salary =30000 – 15000 = Rs 15000
But the actual increase in salary = 31800
Difference =32100 – 31800 = 300
2% = 300
Gugan’s salary =300/2 x 100 = 15000
Harish’s salary =30000 – 15000 = Rs 15000
The marked price of an article is 20% higher than the cost price. A discount of 20% is given on the marked price. In this transaction the seller.- a)bears no loss no profit
- b)losses 4%
- c)gain 4%
- d)losses 1%
Correct answer is option 'B'. Can you explain this answer?
The marked price of an article is 20% higher than the cost price. A discount of 20% is given on the marked price. In this transaction the seller.
a)
bears no loss no profit
b)
losses 4%
c)
gain 4%
d)
losses 1%

|
Telecom Tuners answered |
let cost price = 100 so, marked price = 120
now discount of 20% is given, so sp = 120*80/100 = 96
so % loss = (4/100)*100 = 4 percent
now discount of 20% is given, so sp = 120*80/100 = 96
so % loss = (4/100)*100 = 4 percent
30 litre of solution contains alcohol and water in the ratio 2:3. How much alcohol must be added to the solution to make a solution containing 60% of alcohol?- a)10
- b)12
- c)14
- d)15
Correct answer is option 'D'. Can you explain this answer?
30 litre of solution contains alcohol and water in the ratio 2:3. How much alcohol must be added to the solution to make a solution containing 60% of alcohol?
a)
10
b)
12
c)
14
d)
15

|
Telecom Tuners answered |
alcohol = 30*2/5 = 12 and water = 18 litres
(12 + x)/(30 +x) = 60/100, we will get x = 15
(12 + x)/(30 +x) = 60/100, we will get x = 15
The tank-full petrol in Arun’s motor-cycle last for 10 days. If he starts using 25% more every day, how many days will the tank-full petrol last?- a)4
- b)6
- c)8
- d)10
Correct answer is option 'C'. Can you explain this answer?
The tank-full petrol in Arun’s motor-cycle last for 10 days. If he starts using 25% more every day, how many days will the tank-full petrol last?
a)
4
b)
6
c)
8
d)
10

|
Engineers Adda answered |
Assume – Arun’s motorcycle uses 1L per day and therefore tank’s Capacity = 10L.
25% increased per day= 1+(25/100) = 5/4 ie. 1.25L per day
Days = 10/1.25 = 8
25% increased per day= 1+(25/100) = 5/4 ie. 1.25L per day
Days = 10/1.25 = 8
12 percent of the voters in an election did not cast their votes. In this election there are only two candidates. The winner by obtaining 45% of the total votes and defeated his rival by 2000 votes. The total number of votes in the election.- a)50000
- b)75000
- c)100000
- d)125000
Correct answer is option 'C'. Can you explain this answer?
12 percent of the voters in an election did not cast their votes. In this election there are only two candidates. The winner by obtaining 45% of the total votes and defeated his rival by 2000 votes. The total number of votes in the election.
a)
50000
b)
75000
c)
100000
d)
125000

|
Engineers Adda answered |
12% percent didn’t cast their vote. 45% of total votes get by the winning candidates, so remaining 43% will be scored by his rival. So,
(45/100 -43/100)*P = 2000
P = 100000
(45/100 -43/100)*P = 2000
P = 100000
Weights of two friends A and B are in the ratio of 1:2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?- a)30%
- b)35%
- c)40%
- d)45%
Correct answer is option 'B'. Can you explain this answer?
Weights of two friends A and B are in the ratio of 1:2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?
a)
30%
b)
35%
c)
40%
d)
45%

|
Telecom Tuners answered |
weight of A is x and weight of B is 2x
given that 60 kg weight is the 30% percent increase of the original weight, so
(130/100)*W = 60, W = 600/13 kg (W = original weight)
X + 2x = 600/13, x = 200/13
So weight of A = 200/13 and of B = 400/13
(120/100)*(200/13) + [(100 + a)/100]*(400/13) = 60
Solve for a. We will get a = 35%
given that 60 kg weight is the 30% percent increase of the original weight, so
(130/100)*W = 60, W = 600/13 kg (W = original weight)
X + 2x = 600/13, x = 200/13
So weight of A = 200/13 and of B = 400/13
(120/100)*(200/13) + [(100 + a)/100]*(400/13) = 60
Solve for a. We will get a = 35%
A reduction of 20% in the price of rice enables a housewife to buy 5 kg more for rupees 1200. The reduced price per kg of rice- a)36
- b)45
- c)48
- d)60
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A reduction of 20% in the price of rice enables a housewife to buy 5 kg more for rupees 1200. The reduced price per kg of rice
a)
36
b)
45
c)
48
d)
60
e)
None of these

|
Iq Funda answered |
Step-by-Step Solution
- Define Variables:
- Let p = Original price per kg of rice (₹)
- Reduced price = 20% less than original price = 0.8p
- Determine Quantity Purchased:
- With original price:
- Quantity bought = Total Money / Original Price = ₹1,200 / p = 1200/p kg
- With reduced price:
- Quantity bought = Total Money / Reduced Price = ₹1,200 / (0.8p) = 1500/p kg
- With original price:
- Set Up the Equation Based on the Increase in Quantity:
- Difference in quantity = 5 kg
- Therefore, 1500/p - 1200/p = 5
- Simplify the equation:
- 300/p = 5
- Solve for p:
- p = 300 / 5 = ₹60
- Calculate the Reduced Price:
- Reduced price = 0.8 x Original price = 0.8 x ₹60 = ₹48
Conclusion
The reduced price per kg of rice is ₹48, which corresponds to Option c).
The population of village increases at the rate of 6% per annum. There is an additional increase of 2% in the population due to rural development .Therefore the percentage increase in the population after 2 years will be:- a)15.46%
- b)16.64%
- c)14.46%
- d)12.56%
Correct answer is option 'B'. Can you explain this answer?
The population of village increases at the rate of 6% per annum. There is an additional increase of 2% in the population due to rural development .Therefore the percentage increase in the population after 2 years will be:
a)
15.46%
b)
16.64%
c)
14.46%
d)
12.56%

|
Crack Gate answered |
Total increase = 6+2 = 8%
% increase = 8+8+(8*8/100) = 16+0.64 = 16.64%
% increase = 8+8+(8*8/100) = 16+0.64 = 16.64%
2000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 20% of total students. Then the number of sweets, each student gets.- a)50
- b)100
- c)120
- d)150
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
2000 sweets need to be distributed equally among the school students in such a way that each student gets sweet equal to 20% of total students. Then the number of sweets, each student gets.
a)
50
b)
100
c)
120
d)
150
e)
None of these
|
|
Ravi Singh answered |
Answer – b) 100 Explanation : (20/100)*t*t = 2000 (total students = t)
A got 30% of the maximum marks in an examination and failed by 10 marks.However, B who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?- a)65
- b)75
- c)80
- d)90
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
A got 30% of the maximum marks in an examination and failed by 10 marks.However, B who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
a)
65
b)
75
c)
80
d)
90
e)
None of these
|
|
Anaya Patel answered |
Answer – e) None of these Explanation : (30/100)*T = P -10
(40/100)*T = P + 15
U will get P = 85
(40/100)*T = P + 15
U will get P = 85
Chapter doubts & questions for Percentages - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Percentages - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









