Explore Exams
Login Signup
Sign in Open App

All questions of Analytical Reasoning for UPSC CSE Exam

What is the minimum number of straight lines that is needed to construct the figure?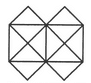 
  
  • a)
    11
  • b)
    13
  • c)
    15
  • d)
    21
Correct answer is option 'B'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
The horizontal lines are AE and JF i.e. 2 in number. The vertical lines are AJ, CH and EF i.e. 3 in number.
The slanting lines are AG, BF, JD, IE, AB, DE, JI and FG i.e. 8 in number.
Total number of straight lines needed to construct the figure = 2 + 3 + 8 = 13.
Clear all your doubts with EduRev

Count the number of squares in the given figure.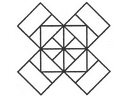 
 
  • a)
    22
  • b)
    20
  • c)
    18
  • d)
    14
Correct answer is option 'C'. Can you explain this answer?

Srishti Nambiar answered
The figure may be labelled as shown.
The squares composed of two components each are BJMI, CKMJ, DLMK and AIML i.e. 4 in number.
The squares composed of three components each are EBMA, BFCM, MCGD and AMDH i.e. 4 in number.
The squares composed of four components each are VWBA, XYCB, ZA1DC and B1C1AD i.e. 4 in number.
The squares composed of seven components each are NOJL, PQKI, RSLJ and TUIK i.e. 4 in number.
There is only one square i.e. ABCD composed of eight components.
There is only one square i.e. EFGH composed of twelve components.
Total number of squares in the figure = 4 + 4 + 4 + 4 + 1 + 1 = 18.

Find the number of triangles in the given figure.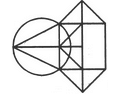
  
  • a)
    10
  • b)
    12
  • c)
    14
  • d)
    16
Correct answer is option 'C'. Can you explain this answer?

Palak Yadav answered
The figure may be labelled as shown.
The simplest triangles are ABJ, ACJ, BDH, DHF, CIE and GIE i.e. 6 in number.
The triangles composed of two components each are ABC, BDF, CEG, BHJ, JHK, JKI and CJI i.e. 7 in number.
There is only one triangle JHI which is composed of four components.
Thus, there are 6 + 7 + 1 = 14 triangles in the given figure.

Find the number of triangles in the given figure.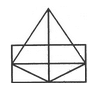
  • a)
    11
  • b)
    13
  • c)
    15
  • d)
    17
Correct answer is option 'C'. Can you explain this answer?

Saumya Singh answered
The figure may be labelled as shown.
The simplest triangles are AKI, AIL, EKD, LFB, DJC, BJC, DHC and BCG i.e. 8 in number.
The triangles composed of two components each are AKL, ADJ, AJB and DBC i.e. 4 in number.
The triangles composed of the three components each are ADC and ABC i.e. 2 in number.
There is only one triangle i.e. ADB composed of four components.
Thus, there are 8+ 4 + 2 + 1= 15 triangles in the figure.

Find the number of triangles in the given figure.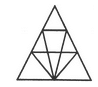
  
  • a)
    12
  • b)
    18
  • c)
    22
  • d)
    26
Correct answer is option 'B'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number.
The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number.
The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number.
There is only one triangle i.e. AGC composed of four components.
There is only one triangle i.e. AFD composed of nine components.
Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.  

How many circles are there in the adjoining figure.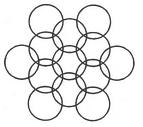
  • a)
    11
  • b)
    12
  • c)
    13
  • d)
    14
Correct answer is option 'C'. Can you explain this answer?

Sneha Kumar answered
The figure may be labelled as shown.
There are 13 circles in the given figure. This is clear from the adjoining figure in which the centres of all the circles in the given figure have been numbered from 1 to 13.

Find the number of triangles in the given figure.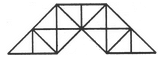 
  
  • a)
    23
  • b)
    27
  • c)
    29
  • d)
    31
Correct answer is option 'C'. Can you explain this answer?

Palak Yadav answered
The figure may be labelled as shown.
The simplest triangles are AHL, LHG, GHM, HMB, GMF, BMF, BIF, CIF, FNC, CNJ, FNE, NEJ, EKJ and JKD i.e. 14 in number.
The triangles composed of two components each are AGH, BHG, HBF, BFG, HFG, BCF, CJF, CJE, JEF, CFE and JED i.e. 11 in number.
The triangles composed of four components each are ABG, CBG, BCE and CED i.e. 4 in number.
Total number of triangles in the given figure = 14 + 11 + 4 = 29.

In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed. 
  
  • a)
    6
  • b)
    7
  • c)
    8
  • d)
    1
Correct answer is option 'C'. Can you explain this answer?

Palak Yadav answered
The figure may be labelled as shown.
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.
The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number.
Thus, 6 + 2 = 8 squares will be formed.

Find the number of triangles in the given figure.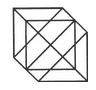
  
  • a)
    18
  • b)
    20
  • c)
    24
  • d)
    27
Correct answer is option 'C'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown. 
The simplest triangles are IJO, BCJ, CDK, KQL, MLQ, GFM, GHN and NIO i.e. 8 in number.
The triangles composed of two components each are ABO, AHO, NIJ, IGP, ICP, DEQ, FEQ, KLM, LCP and LGP i.e.10 in number.
The triangles composed of four components each are HAB, DEF, LGI, GIC, ICL and GLC i.e. 6 in number.
Total number of triangles in the figure = 8 + 10 + 6 = 24.

What is the minimum number of different colours required to paint the given figure such that no two adjacent regions have the same colour?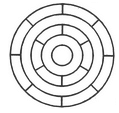 
  • a)
    3
  • b)
    4
  • c)
    5
  • d)
    6
Correct answer is option 'A'. Can you explain this answer?

Bhargavi Singh answered
The figure may be labelled as shown.
The regions A, C, E and G can have the same colour say colour 1.
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2.
The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3.
The regions J, L and N can have the same colour (different from colour 3) say colour 1.
The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2.
The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3.
The region Q can have any of the colours 1 or 2.
Minimum number of colours required is 3.

Find the minimum number of straight lines required to make the given figure.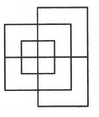
 
  • a)
    13
  • b)
    15
  • c)
    17
  • d)
    19
Correct answer is option 'A'. Can you explain this answer?

Baishali Choudhury answered
The figure may be labelled as shown.
The horizontal lines are IJ, AB, EF, MN, HG, DC and LK i.e. 7 in number.
The vertical lines are AD, EH, IL, FG, BC and JK i.e. 6 in number.
Thus, there are 7 + 6 = 13 straight lines in the figure.

Determine the number of rectangles and hexagons in the given figure.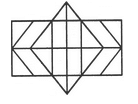
 
  • a)
    30, 5
  • b)
    32, 3
  • c)
    28, 5
  • d)
    30, 3
Correct answer is option 'A'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
Rectangles:
The simplest rectangles are CVSR, VETS, RSWM and STKW i.e. 4 in number.
The rectangles composed of two components each are CETR, VEKW, RTKM and CVWM i.e. 4 in number.
The rectangles composed of three components each are ACRP, PRMO, EGHT and THIK i.e. 4 in number.
The rectangles composed of four components each are CEKM, AVSP,PSWO, VGHS and SHIW i.e. 5 in number.
The rectangles composed of five components each are AETP, PTKO, CGHR and RHIM i.e. 4 in number.
The rectangles composed of six components each are ACMO and EGIK i.e. 2 in number.
The rectangles composed of eight components each are AGHP, PHIO, AVWO and VGIW i.e. 4 in number.
The rectangles composed of ten components each are AEKO and CGIM i.e. 2 in number.
AGIO is the only rectangle having sixteen components.
Total number of rectangles in the given figure
= 4 + 4 + 4 + 5 + 4 + 2 + 4 + 2 + 1 = 30.
Hexagons:
The hexagons in the given figure are CDEKLM, CEUKMQ, CFHJMQ, BEUKNP and BFHJNP.
So, there are 5 hexagons in the given figure.

Count the number of triangles and squares in the given figure.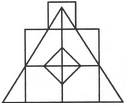 
  
  • a)
    21 triangles, 7 squares
  • b)
    18 triangles, 8 squares
  • c)
    20 triangles, 8 squares
  • d)
    22 triangles, 7 squares
Correct answer is option 'A'. Can you explain this answer?

Palak Yadav answered
The figure may be labelled as shown. 
Triangles :
The simplest triangles are BPN, PNE, ABM, EFG, MLK, GHI, QRO, RSO, STO and QTO i.e. 10 in number.
The triangles composed of two components each are BPE, TQR, QRS, RST and STQ i.e. 5 in number.
The triangles composed of three components each are MPO and GPO i.e. 2 in number.
The triangles composed of six components each are LPJ, HPJ and MPG i.e. 3 in number.
There is only one triangle LPH composed of twelve components.
Total number of triangles in the figure = 10 + 5 - 2 + 3 + 1 = 21.
Squares :
The squares composed of two components each are KJOM and JIGQ i.e. 2 in number.
The squares composed of three components each are ANOM, NFGO and CDEB i.e.3 in number.
There is only one square i.e. QRST composed of four components.
There is only one square i.e. AFIK composed of ten components.
Total number of squares in the figure = 2 + 3 + 1 + 1 = 7.

Find the number of triangles in the given figure.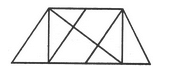
 
  • a)
    8
  • b)
    10
  • c)
    12
  • d)
    14
Correct answer is option 'D'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
The simplest triangles are AHG, AIG, AIB, JFE, CJE and CED i.e. 6 in number.
The triangles composed of two components each are ABG, CFE, ACJ and EGI i.e. 4 in number.
The triangles composed of three components each are ACE, AGE and CFD i.e. 3 in number.
There is only one triangle i.e. AHE composed of four components.
Therefore, There are 6 + 4 + 3 + 1 = 14 triangles in the given figure.

Count the number of triangles and squares in the given figure.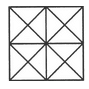 
  
  • a)
    44 triangles, 10 squares
  • b)
    14 triangles, 16 squares
  • c)
    27 triangles, 6 squares
  • d)
    6 triangles, 9 squares
Correct answer is option 'A'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
Triangles :
The simplest triangles are AEI, EOI, OHI, HAI, EBJ, BFJ, FOJ, OEJ, HOL, OGL, GDL, DHL, OFK, FCK, CGK and GOK i.e. 16 in number.
The triangles composed of two components each are HAE, AEO, EOH, OHA, OEB, EBF, BFO, FOE, DHO, HOG, OGD, GDH, GOF, OFC, FCG and CGO i.e. 16 in number.
The triangles composed of four components each are HEF, EFG, FGH, GHE, ABO, BGO, CDO and DAO i.e. 8 in number.
The triangles composed of eight components each are DAB, ABC, BCD and CDA i.e. 4 in number.
Total number of triangles in the figure = 16 + 16 + 8 + 4 = 44.
Squares :
The squares composed of two components are HIOL, IEJO, JFKO and KGLO i.e. 4 in number.
The squares composed of four components are AEOH, EBFO, OFGC and HOGD i.e.4 in number.
There is only one square EFGH which is composed of eight components.
There is only one square ABCD which is composed of sixteen components.
Total number of squares in the figure = 4 + 4 + 1 + 1 = 10.

Count the number of rectangles in the given figure.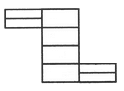
  
  • a)
    8
  • b)
    17
  • c)
    18
  • d)
    20
Correct answer is option 'C'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
 
The simplest rectangles are ABQP, PQNO, BCDN, NDEM, MEFL, LFJK, FGHR and RHIJ i.e. 8 in number.
The rectangles composed of two components each are ABNO, BCEM, NDFL, MEJK and FGIJ i.e. 5 in number.
The rectangles composed of three components each are ACDO, BCFL, NDJK and LGIK i.e. 4 in number.
There is only one rectangle i.e. BCJK composed of four components.
Total number of rectangles in the figure = 8 + 5 + 4 + 1 = 18.

Find the number of triangles in the given figure.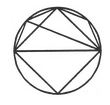 
  
  • a)
    8
  • b)
    10
  • c)
    11
  • d)
    12
Correct answer is option 'B'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
The simplest triangles are ABG, BCG, CGE, CDE, AGE and AEF i.e. 6 in number.
The triangles composed of two components each are ABE, ABC, BCE and ACE i.e. 4 in number.
There are 6 + 4 = 10 triangles in the figure.

Find the number of triangles in the given figure.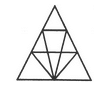 
  
  • a)
    16
  • b)
    18
  • c)
    14
  • d)
    15
Correct answer is option 'B'. Can you explain this answer?

Akanksha Ahuja answered
The figure may be labelled as shown.
The simplest triangles are BFG, CGH, EFM, FMG, GMN, GHN, HNI, LMK, MNK and KNJ i.e. 10 in number.
The triangles composed of three components each are FAK and HKD i.e. 2 in number.
The triangles composed of four components each are BEN, CMI, GLJ and FHK i.e. 4 in number.
The triangles composed of eight components each are BAJ and OLD i.e. 2 in number.
Thus, there are 10 + 2 + 4 + 2 = 18 triangles in the given figure.

Count the number of triangles and squares in the given figure.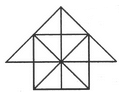 
   
  • a)
    26 triangles, 5 squares
  • b)
    28 triangles, 5 squares
  • c)
    26 triangles, 6 squares
  • d)
    28 triangles, 6 squares
Correct answer is option 'D'. Can you explain this answer?

Gargi Saha answered
The figure may be labelled as shown.
Triangles:
The simplest triangles are JBO, BKO, KDO, DFO, FGO, GHO, HIO, IJO, ABJ, BCK, CKD and DEF i.e.12 in number.
The triangles composed of two components each are IBO, BDO, DGO, GIO, ABO, CDO, CBO, CBD and DEO i.e. 9 in number.
The triangles composed of four components each are IBD, BDG, DGI, GIB, ACO and COE i.e. 6 in number.
There is only one. triangle i.e. ACE composed of eight components.
Thus, there are 12 + 9 + 6 + 1 = 28 triangles in the given figure.
Squares:
The squares composed of two components each are BKOJ, KDFO, OFGH and JOHI i.e. 4 in number.
There is only one square i.e. CDOB composed of four components.
There is only one square i.e. BDGI composed of eight components.
Thus, there are 4 + 1 + 1 = 6 squares in the given figure.

Find the number of triangles in the given figure.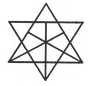
  
  • a)
    21
  • b)
    23
  • c)
    25
  • d)
    27
Correct answer is option 'D'. Can you explain this answer?

Bhargavi Singh answered
The figure may be labelled as shown.
The simplest triangles are ABL, BCD, DEF, FGP, PGH, QHI, JQI, KRJ and LRK i.e. 9 in number.
The triangles composed of two components each are OSG, SGQ, SPI, SRI, KSQ, KMS, FGH, JHI and JKL i.e. 9 in number.
There is only one triangle i.e. KSG which is composed of four components.
The triangles composed of five components each are NEI, ANI, MCG and KCO i.e. 4 in number.
The triangles composed of six components each are GMK and KOG i.e. 2 in number.
There is only one triangle i.e. AEI composed of ten components.
There is only one triangle i.e. KCG composed of eleven components.
Therefore, Total number of triangles in the given figure = 9 + 9+1 + 4 + 2+1 + 1 = 27.

Chapter doubts & questions for Analytical Reasoning - UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Analytical Reasoning - UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making in English & Hindi are available as part of UPSC CSE exam. Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Top Courses UPSC CSE

Related UPSC CSE Content

© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup