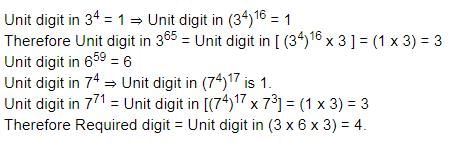All Exams >
UPSC >
UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making >
All Questions
All questions of Unit Digit Calculation for UPSC CSE Exam
Why does the narrator call the two boys as gentlemen?- a)Because they were rich
- b)Because they had dressed properly like a gentlemen
- c)Because they had lots of property
- d)Because they has gentlemen like qualities
Correct answer is option 'D'. Can you explain this answer?
Why does the narrator call the two boys as gentlemen?
a)
Because they were rich
b)
Because they had dressed properly like a gentlemen
c)
Because they had lots of property
d)
Because they has gentlemen like qualities
|
|
North Summer answered |
Because they had the qualities of a gentleman .
How far was Poleta from the two boys' workplace?- a)10 kms
- b)20 kms
- c)30 kms
- d)40 kms
Correct answer is option 'C'. Can you explain this answer?
How far was Poleta from the two boys' workplace?
a)
10 kms
b)
20 kms
c)
30 kms
d)
40 kms

|
Saxena Aastha answered |
C is correct option read ur textbook
For an integer n = 216 * 313 * 55 * 75 * 113, what is the value of the first non-zero digit from the right?- a)1
- b)2
- c)4
- d)6
- e)8
Correct answer is option 'E'. Can you explain this answer?
For an integer n = 216 * 313 * 55 * 75 * 113, what is the value of the first non-zero digit from the right?
a)
1
b)
2
c)
4
d)
6
e)
8
|
|
Aarav Sharma answered |
Given:
- An integer n whose prime-factorized form is 216 * 313 * 55 * 75 * 113
To find: The first non-zero digit from the right
Approach:
- To answer the question, we first need to understand why, in the first place, the rightmost digits of n will be 0.
- The answer lies in the presence of both 2 and 5 in n
- So, we’ll calculate the number of zeros in n
- Then, we will separate the prime numbers of n (along with their powers) that do not contribute to these zeros. The first non-zero digit from the right will be equal to the units digit of the product of these separated prime numbers (along with their powers)
- Using the cyclicity of these separated prime numbers, we’ll get to the answer
Working Out:
- Calculating the number of zeros in n
- The zeros result from the product of 2 and 5
- Each zero requires one 2 and one 5
- In n, there are sixteen 2s and five 5s
- So, 5 is the limiting factor in the making of zeros
- The number of zeros will be equal to the number of 5s in n
- So, there will be five zeros in n
- All the five 5s and five of the sixteen 2s in n will be used up by the zeros
- The zeros result from the product of 2 and 5
- Separating the prime numbers that do not contribute to the zeros
- As noted above, all the five 5s and five 2s of n are used up by zeros
- So, the prime numbers of n (along with powers) that do not contribute to the zeros are:
- 211
- 313
- 75
- 113
- So, the right-most non-zero digit of n is actually the units digit of the product 211*313*75*113
- The units digit of this product will be obtained by multiplying the units digits of:
- 211
- 313
- 75
- 113
- Using the cyclicity of the separated prime numbers to get the answer
- Finding Units digit of 211
- 211 = 24*2+3
- So, units digit of 211 = units digit of 23 = 8
- Finding Units digit of 211
- Finding Units digit of 313
- 313 = 34*3+1
- So, units digit of 313 = units digit of 31 = 3
- Finding Units digit of 75
- 75 = 74+1
- So, units digit of 75 = units digit of 71 = 7
- Finding Units digit of 113
- Units digit = 1
- Finding units digit of the product 211*313*75*113
- = Units digit of (8*3*7*1)
- = 8
Looking at the answer choices, we see that the correct answer is Option E
The digit in the unit place of the number represented by (795 * 358) is- a)7
- b)0
- c)6
- d)4
Correct answer is option 'A'. Can you explain this answer?
The digit in the unit place of the number represented by (795 * 358) is
a)
7
b)
0
c)
6
d)
4
|
|
Prakhya Shrivastava answered |
We khow that by increasing power of 7, repeating cycle of 7,9,3,1 respectively comes in unit place... thus at 95 power of 7 unit digit should be 3
i.e.
unit digit of 7^95 = 3
Similarly by increasing power of 3,repeating cycle of 3,9,7,1 respectively comes in unit place hence at 58 power of three unit digit should be 9
i.e.
unit digit of 3^58 = 9
Now unit digit of (7^95 × 3^58) = 3×9 = 27
i.e. 7 is the digit in unit place if we solve (7^95 × 3^58).
Hence option (a) is correct
i.e.
unit digit of 7^95 = 3
Similarly by increasing power of 3,repeating cycle of 3,9,7,1 respectively comes in unit place hence at 58 power of three unit digit should be 9
i.e.
unit digit of 3^58 = 9
Now unit digit of (7^95 × 3^58) = 3×9 = 27
i.e. 7 is the digit in unit place if we solve (7^95 × 3^58).
Hence option (a) is correct
What is the units digit of 3961?- a)9
- b)1
- c)3
- d)7
Correct answer is option 'A'. Can you explain this answer?
What is the units digit of 3961?
a)
9
b)
1
c)
3
d)
7
|
|
Abhishek Phogat answered |
We know that odd power of 9 gives 9 at unit place but even power gives 1 at unit place
Also, 61 is odd hence unit place is 9...
Also, 61 is odd hence unit place is 9...
What will be the units digit, when the product of the first 10 natural numbers is divided by 100?
- a)0
- b)2
- c)5
- d)6
- e)8
Correct answer is option 'E'. Can you explain this answer?
What will be the units digit, when the product of the first 10 natural numbers is divided by 100?
a)
0
b)
2
c)
5
d)
6
e)
8

|
T.S Academy answered |
1x2x3x4x5x6x7x8x9x10 so clearly they have 2 zeroes
one from 10 and other from 2x5
so multiply then 3x4x6x7x8x9 will give 8 as unit digit
one from 10 and other from 2x5
so multiply then 3x4x6x7x8x9 will give 8 as unit digit
The unit digit in the product (784 x 618 x 917 x 463) is:- a)2
- b)3
- c)4
- d)5
- e)6
Correct answer is option 'A'. Can you explain this answer?
The unit digit in the product (784 x 618 x 917 x 463) is:
a)
2
b)
3
c)
4
d)
5
e)
6

|
Sanskriti Ahuja answered |
Unit digit in the given product = Unit digit in (4 x 8 x 7 x 3) = (672) = 2
Find the product of 57 x 61 x 39 x 53.- a)7086751
- b)7086953
- c)7186959
- d)7186965
- e)7286977
Correct answer is option 'C'. Can you explain this answer?
Find the product of 57 x 61 x 39 x 53.
a)
7086751
b)
7086953
c)
7186959
d)
7186965
e)
7286977
|
|
Sanchita Gupta answered |
Product of 57 x 61 x 39 x 53 can be evaluated as follows:
Step 1: Break each number into prime factors
57 = 3 x 19
61 = 61
39 = 3 x 13
53 = 53
Step 2: Multiply all the prime factors together
3 x 19 x 61 x 3 x 13 x 53 = 3 x 3 x 19 x 13 x 53 x 61
Step 3: Arrange the factors in ascending order
3 x 3 x 13 x 19 x 53 x 61
Step 4: Multiply the factors together
3 x 3 x 13 x 19 x 53 x 61 = 7,186,959
Therefore, the correct answer is option C, which is 7,186,959.
Step 1: Break each number into prime factors
57 = 3 x 19
61 = 61
39 = 3 x 13
53 = 53
Step 2: Multiply all the prime factors together
3 x 19 x 61 x 3 x 13 x 53 = 3 x 3 x 19 x 13 x 53 x 61
Step 3: Arrange the factors in ascending order
3 x 3 x 13 x 19 x 53 x 61
Step 4: Multiply the factors together
3 x 3 x 13 x 19 x 53 x 61 = 7,186,959
Therefore, the correct answer is option C, which is 7,186,959.
What is the unit digit in 7105 ?- a)1
- b)5
- c)7
- d)9
Correct answer is option 'C'. Can you explain this answer?
What is the unit digit in 7105 ?
a)
1
b)
5
c)
7
d)
9

|
Rithika Rane answered |
Explanation:
Unit digit in 7105 = Unit digit in [ (74)26 x 7 ]
But, unit digit in (74)26 = 1
 Unit digit in 7105 = (1 x 7) = 7
Unit digit in 7105 = (1 x 7) = 7Find the units digit of 53n + 95m, where m and n are positive integers - m is an odd integer
- n is an even integer
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
Find the units digit of 53n + 95m, where m and n are positive integers
- m is an odd integer
- n is an even integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Kritika Desai answered |
Given: 53n 95m, where m and n are positive integers
m is an odd integer
n is an even integer
To find: Units digit of 53n 95m
Approach:
We need to find the units digit of the given expression which is the remainder obtained when the expression is divided by 10.
Statement 1: m = 1
If m = 1, then 95m = 95 and its units digit is 5.
Now, we need to find the units digit of 53n 95. If we observe the units digit of powers of 5, it repeats after every 4 powers. The units digit of 5, 5^2, 5^3, 5^4, 5^5, … is 5, 25, 125, 625, 3125, …
Hence, the units digit of 53n 95 will depend on the value of n. If n = 2, then 53n = 253 and the units digit of 253 + 5 = 8. If n = 4, then 53n = 2053 and the units digit of 2053 + 5 = 8. If n = 6, then 53n = 20553 and the units digit of 20553 + 5 = 8. The pattern repeats after every 4 values of n. Hence, the units digit of the given expression will be 8 when m = 1 and n is even.
Therefore, statement 1 alone is sufficient.
Statement 2: n = 2
If n = 2, then 53n = 253 and the units digit of 53n is 3.
Now, we need to find the units digit of 53n 95m. If we observe the units digit of powers of 9, it repeats after every 2 powers. The units digit of 9, 9^2, 9^3, 9^4, … is 9, 81, 729, 6561, …
Hence, the units digit of 95m will depend on the value of m. If m = 1, then the units digit of 95m + 3 = 8. If m = 3, then the units digit of 95m + 3 = 2. The pattern repeats after every 2 values of m. Hence, the units digit of the given expression will be 8 when n = 2 and m is odd.
Therefore, statement 2 alone is not sufficient.
Hence, the correct answer is option A. Statement 1 alone is sufficient but statement 2 alone is not sufficient.
m is an odd integer
n is an even integer
To find: Units digit of 53n 95m
Approach:
We need to find the units digit of the given expression which is the remainder obtained when the expression is divided by 10.
Statement 1: m = 1
If m = 1, then 95m = 95 and its units digit is 5.
Now, we need to find the units digit of 53n 95. If we observe the units digit of powers of 5, it repeats after every 4 powers. The units digit of 5, 5^2, 5^3, 5^4, 5^5, … is 5, 25, 125, 625, 3125, …
Hence, the units digit of 53n 95 will depend on the value of n. If n = 2, then 53n = 253 and the units digit of 253 + 5 = 8. If n = 4, then 53n = 2053 and the units digit of 2053 + 5 = 8. If n = 6, then 53n = 20553 and the units digit of 20553 + 5 = 8. The pattern repeats after every 4 values of n. Hence, the units digit of the given expression will be 8 when m = 1 and n is even.
Therefore, statement 1 alone is sufficient.
Statement 2: n = 2
If n = 2, then 53n = 253 and the units digit of 53n is 3.
Now, we need to find the units digit of 53n 95m. If we observe the units digit of powers of 9, it repeats after every 2 powers. The units digit of 9, 9^2, 9^3, 9^4, … is 9, 81, 729, 6561, …
Hence, the units digit of 95m will depend on the value of m. If m = 1, then the units digit of 95m + 3 = 8. If m = 3, then the units digit of 95m + 3 = 2. The pattern repeats after every 2 values of m. Hence, the units digit of the given expression will be 8 when n = 2 and m is odd.
Therefore, statement 2 alone is not sufficient.
Hence, the correct answer is option A. Statement 1 alone is sufficient but statement 2 alone is not sufficient.
What is the rightmost non-zero digit of 9042?- a)0
- b)1
- c)2
- d)8
- e)9
Correct answer is option 'B'. Can you explain this answer?
What is the rightmost non-zero digit of 9042?
a)
0
b)
1
c)
2
d)
8
e)
9
|
|
Ayush Das answered |
Solution:
We need to find the rightmost non-zero digit of the number 9042.
To find the rightmost non-zero digit of a number, we need to find the remainder when the number is divided by 10.
So, we divide 9042 by 10 to get the remainder:
9042 ÷ 10 = 904 remainder 2
So, the rightmost digit of 9042 is 2, which is the answer.
Therefore, the correct option is (b) 2.
We need to find the rightmost non-zero digit of the number 9042.
To find the rightmost non-zero digit of a number, we need to find the remainder when the number is divided by 10.
So, we divide 9042 by 10 to get the remainder:
9042 ÷ 10 = 904 remainder 2
So, the rightmost digit of 9042 is 2, which is the answer.
Therefore, the correct option is (b) 2.
Find the unit digit of (7493263)x(15129)- a)3
- b)9
- c)7
- d)1
Correct answer is option 'C'. Can you explain this answer?
Find the unit digit of (7493263)x(15129)
a)
3
b)
9
c)
7
d)
1

|
Dipika Gupta answered |
Answer: c)7
Solution:
The given product is (7493263)x(15129)
Required unit digit = the unit digit of(3263)x(129) ...(1)
In the value of 3 to the power 4, we have the unit digit as 1.
so, we can rewrite (3263) = [3(4x65 + 3)] = [(34)65] x (33)
Then from eqn(1),
The unit digit of(3263)x(129) = The unit digit of[(34)65] x (33) x 129
= The unit digit of[165] x 27 x 1
= The unit digit of 1 x 7 x 1 = 7
Hence, the answer is 7.
The given product is (7493263)x(15129)
Required unit digit = the unit digit of(3263)x(129) ...(1)
In the value of 3 to the power 4, we have the unit digit as 1.
so, we can rewrite (3263) = [3(4x65 + 3)] = [(34)65] x (33)
Then from eqn(1),
The unit digit of(3263)x(129) = The unit digit of[(34)65] x (33) x 129
= The unit digit of[165] x 27 x 1
= The unit digit of 1 x 7 x 1 = 7
Hence, the answer is 7.
For any positive number x, the function [x] denotes the greatest integer less than or equal to x. For example, [1] = 1, [1.367] = 1 and [1.999] = 1.If k is a positive integer such that k2 is divisible by 45 and 80, what is the units digit of 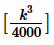
- a)0
- b)1
- c)27
- d)54
- e)Cannot be determined
Correct answer is option 'E'. Can you explain this answer?
For any positive number x, the function [x] denotes the greatest integer less than or equal to x. For example, [1] = 1, [1.367] = 1 and [1.999] = 1.
If k is a positive integer such that k2 is divisible by 45 and 80, what is the units digit of 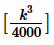
a)
0
b)
1
c)
27
d)
54
e)
Cannot be determined

|
Divey Sethi answered |
Given:
- Positive integer k (so, k > 0)
- k2 is divisible by 45
- k2 is divisible by 80
- The function [x]
To find: The units digit of 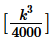
Approach:
- To find the units digit of [x], we need to know or at least have some idea of the value of x. So, in order to answer the question, we need to find the value or at least a clue about the value of the number
- This number contains k3, which is the cube of a positive integer. However, the given information is about k2. Like in all questions that involve divisibility information about different powers of an integer, we’ll work out information about k3 as under:
- First use the information given about k2 to infer about the prime-factorized form of k.
- Then, by cubing the prime-factorized expression of k, get an expression for k3
Working Out:
- Inferring the prime-factorized expression for k from the given information
- Let k = P1a * P2b *P3c *P4d . . .where P1, P2 etc. are prime numbers and a, b . . . are non-negative integers
- Therefore, k2 = P12a * P22b *P32c *P42d . . .
- We are given that k2 is divisible by 45
- 45 = 32*5
- This means, P1 = 3 and 2a ≥ 2
- That is, a ≥ 1
- And, P2 = 5 and 2b ≥ 1
- That is,
- Since b is an integer, minimum possible value of b = 1
- That is,
- Therefore, k = (31*51)(3x*5y* P3c *P4d . . .) where x and y are non-negative integers
- Note: In the above expression, we’ve taken 31 and 51 outside the remaining expression in order to emphasize the fact that k definitely does contain 31 and 51, whether or not it contains higher powers of 3 and 5
- So far, we’ve inferred that: k = (31*51)(3x*5y* P3c *P4d . . .)
- So, k2 = (32*52)(32x*52y* P32c *P42d . . .)
- We are also given that k2 is divisible by 80
- 80 = 24*5
- This means, P3 = 2 and 2c ≥ 4
- That is, c ≥ 2
- So, k = (22*31*51)(2z*3x*5y* P4d . . .), where x, y, z, d etc. are non-negative integers
- Inferring the expression for k3
- Using the expression for k inferred above, we can write:
- k3 = (26*33*53)(23z*33x*53y* P43d . . .),
- Drawing inferences about the value of
- 4000 = 25*53
- Looking at the expression for k3 above, we see that k3 will be divisible by 4000
- So,
is an integer
- The value of this integer will be (21*33)(23z*33x*53y* P43d . . .)
- So,
= (21*33)(23z*33x*53y* P43d . . .)
- If y ≥ 1, then the units digit of the right hand side expression will be 0 (because the units digit of 2*5 is 0. Note that the above expression has at least one 2)
- But if y = 0, then the units digit will depend on the power of 2, 3 and the value and powers of any other prime numbers that are present in k
-
- Thus, we are not able to determine a unique value of the units digit of
- Looking at the answer choices, we see that the correct answer is Option E
- Let k = P1a * P2b *P3c *P4d . . .where P1, P2 etc. are prime numbers and a, b . . . are non-negative integers
If a and b are positive integers, is the sum a + b divisible by 4? - When the sum 23a + 25b is divided by 10, the remainder is 8
- When 22b is divided by 10, the remainder is 8
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
If a and b are positive integers, is the sum a + b divisible by 4?
- When the sum 23a + 25b is divided by 10, the remainder is 8
- When 22b is divided by 10, the remainder is 8
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Amar Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: Integers a, b > 0
To find: If a + b is divisible by 4?
Step 3: Analyze Statement 1 independently
Statement 1 says that ‘When the sum 23a + 25b is divided by 10, the remainder is 8’
- Now, we know that when an integer is divided by 10, the remainder is equal to the units digit of that integer
- For example, when 25 is divided by 10, the remainder is 5 (the units digit of 25)
- So, from Statement 1, we can infer that the units digit of the sum 23a + 25b is 8
- Now, the units digit of 25b will always be 5, for all possible values of the positive integer b
- Therefore, the units digit of the term 23a must be 3
- Now, the units digit of 23a comes from 3a
- For the units digit to be 3, a must be of the form 4k + 1, where k is a non-negative integer
- Thus, from Statement 1, we have inferred that a is of the form 4k + 1. However, since we do not yet know about the value of b, we cannot comment if the sum a + b is divisible by 4 or not.
- So, Statement 1 is not sufficient.
Step 4: Analyze Statement 2 independently
Statement 2 says that ‘When 22b is divided by 10, the remainder is 8’
- We know that when an integer is divided by 10, the remainder is equal to the units digit of that integer
- So, from Statement II, we can infer that the units digit of 22b is 8
- Now, the units digit of 22b comes from 2b
- For the units digit to be 8, b must be of the form 4m + 3, where m is a non-negative integer
- Thus, from Statement 2, we have inferred that b is of the form 4m + 3. However, since we do not know about the value of a, we cannot comment if the sum a + b is divisible by 4 or not.
- So, Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, we inferred that a is of the form 4k + 1
- From Statement 2, we inferred that b is of the form 4m + 3
- So, combining the 2 statements, we observe that the sum a + b is of the form 4k + 4m + 4
- Therefore the sum a + b is indeed divisible by 4
- Since we’ve arrived at a unique answer to the question, the two statements together are sufficient.
Answer: Option C
If the number 653 xy is divisible by 90, then (x + y) = ?- a)2
- b)3
- c)4
- d)6
- e)5
Correct answer is option 'C'. Can you explain this answer?
If the number 653 xy is divisible by 90, then (x + y) = ?
a)
2
b)
3
c)
4
d)
6
e)
5

|
Ameya Banerjee answered |
90 = 10 x 9
Clearly, 653xy is divisible by 10, so y = 0
Now, 653x0 is divisible by 9.
So, (6 + 5 + 3 + x + 0) = (14 + x) is divisible by 9. So, x = 4.
Hence, (x + y) = (4 + 0) = 4.
Clearly, 653xy is divisible by 10, so y = 0
Now, 653x0 is divisible by 9.
So, (6 + 5 + 3 + x + 0) = (14 + x) is divisible by 9. So, x = 4.
Hence, (x + y) = (4 + 0) = 4.
Find the unit digit of (432)412 × (499)431- a)1
- b)3
- c)2
- d)5
- e)4
Correct answer is option 'E'. Can you explain this answer?
Find the unit digit of (432)412 × (499)431
a)
1
b)
3
c)
2
d)
5
e)
4
|
|
Jaya Nambiar answered |
To find the unit digit of (432)412, we need to find the remainder when (432)412 is divided by 10.
Let's first look at the unit digits of powers of 2:
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16 (unit digit is 6)
2^5 = 32 (unit digit is 2)
2^6 = 64 (unit digit is 4)
2^7 = 128 (unit digit is 8)
2^8 = 256 (unit digit is 6)
We notice that the unit digit of 2^n repeats in cycles of 4: 2, 4, 8, 6.
Now, let's look at the exponent 412. We can write it as:
412 = 4(100) + 1(10) + 2
So we need to find the remainder when (432)412 is divided by 10, which is the same as finding the remainder when (432)4(100) * (432)1(10) * (432)2 is divided by 10.
Using the cycles of 2^n unit digits, we know that the unit digit of (432)4(100) is 6, and the unit digit of (432)1(10) is 2.
Now we just need to find the unit digit of (432)2.
(432)2 = 186624
The unit digit is 4.
So the remainder when (432)412 is divided by 10 is the same as the remainder when 6 * 2 * 4 is divided by 10.
6 * 2 * 4 = 48
The unit digit of 48 is 8.
Therefore, the unit digit of (432)412 is 8.
Let's first look at the unit digits of powers of 2:
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16 (unit digit is 6)
2^5 = 32 (unit digit is 2)
2^6 = 64 (unit digit is 4)
2^7 = 128 (unit digit is 8)
2^8 = 256 (unit digit is 6)
We notice that the unit digit of 2^n repeats in cycles of 4: 2, 4, 8, 6.
Now, let's look at the exponent 412. We can write it as:
412 = 4(100) + 1(10) + 2
So we need to find the remainder when (432)412 is divided by 10, which is the same as finding the remainder when (432)4(100) * (432)1(10) * (432)2 is divided by 10.
Using the cycles of 2^n unit digits, we know that the unit digit of (432)4(100) is 6, and the unit digit of (432)1(10) is 2.
Now we just need to find the unit digit of (432)2.
(432)2 = 186624
The unit digit is 4.
So the remainder when (432)412 is divided by 10 is the same as the remainder when 6 * 2 * 4 is divided by 10.
6 * 2 * 4 = 48
The unit digit of 48 is 8.
Therefore, the unit digit of (432)412 is 8.
For any positive number n, the function #n represents the value of the number n rounded to the nearest integer. If k is a positive number, what is the units digit of #k?(1) #(10k) = 10k(2) #(100k) is 10300.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
For any positive number n, the function #n represents the value of the number n rounded to the nearest integer. If k is a positive number, what is the units digit of #k?
(1) #(10k) = 10k
(2) #(100k) is 10300.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Manasa Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Let k = n + a.bcde. . . , where n is a multiple of 10 and a, b, c, d, e etc. denote the units, tenths, hundredths, thousandths, ten-thousandths digits of k respectively.
- Example: Say k is equal to 123.789. We can also write this value as 120 + 3.789. This form is comparable to n + a.bcde . . .
- So, n denotes the value of all the digits at the tens, hundreds, thousands and higher place values (if k = 123.789, n = 120; if k = 3456.987, n = 3450; if k = 43789.34, n = 43780 and so on)
- We have split k into n and a.bcde. . . because the question doesn’t indicate whether the magnitude of k is in tens or hundreds or thousands etc. (that is, is k a number like 12.345 or like 123.789 or like 3456.987 etc.) This knowledge is not important either because all the action is happening at the units digit and the digits to the right of the decimal point. So, we’ve simply expressed the value of all the digits at the tens, hundreds, thousands and higher place values in a single term n
- #k =
- n + a, if b < 5
- n + (a+1) if b ≥ 5
To find:
- The units digit of #k
- Since n is a multiple of 10, from the expression of #k, we can say that the units digit of #k =
- a, if b < 5
- a + 1, if b ≥ 5
Thus, to answer the question, we need to know the value of a and whether b < 5 or not
Step 3: Analyze Statement 1 independently
(1) #(10k) = 10k
- 10k = 10n + ab.cde. . .
- Since a is now the tens digit and b is the units digit, we can write
10k = 10n + 10a + b.cde. . .
10k = 10(n+a) + b.cde. . .
- Applying the definition of the function #n, we can write:
- #(10k) =
- 10(n+a) + b if c < 5
- 10(n+a) + (b+1) if c ≥ 5
- #(10k) =
- We are given that #(10k) = 10k.
- #(10k) = 10(n+a) + b.cde . . .
- If c < 5, then by substituting the value of #(10k) in the above equation, we get:
- 10(n+a) + b = 10(n+a) + b.cde. . .
- b = b + 0.cde. . .
- This implies, c = d = e . . .= 0
- Thus, k is a number of the form n + a.b, where b is the sole digit after the decimal point
- If c ≥ 5, then by substituting the value of #(10k) in the above equation, we get:
- 10(n+a) + (b+1) = 10(n+a) + b.cde. . .
- b +1 = b + 0.cde . . .
- 1 = 0.cde . . .
- For no values of digits c, d, e . . . will the above equation be satisfied.
- Therefore, this case is not possible
- Thus, from Statement 1, we conclude that k is a number of the form n + a.b, where b is the sole digit after the decimal point
- However, we still don’t know the value of a or whether b is less than 5 or not.
So, Statement 1 alone is not sufficient.
Step 4: Analyze Statement 2 independently
(2) #(100k) is 10300.
- 100k = 100n + abc.de. . .
- 100k = (100n + 100a + 10b) + c.de. . .
- Applying the definition of the function #n, we can write:
- #(100k) =
- (100n + 100a + 10b) + c if d < 5
- (100n + 100a + 10b) + (c+1) if d ≥ 5
- #(100k) =
- We are given that #(100k) = 10300
- If d < 5, then we can write
- (100n + 100a + 10b) + c = 10300
- Remember that in the above expression, a, b and c are digits (therefore, lie between 0 and 9, inclusive) whereas n is a multiple of 10.
- Comparing the units digits on both sides of the equation, we get: c = 0
- Comparing the tens digits on both sides of the equation, we get: b = 0
- Comparing the hundreds digits on both sides of the equation, we get: a = 3
- Since b < 5 in this case, the units digit of #k = a = 3
- If d < 5, then we can write
- If d ≥ 5, then we can write
- (100n + 100a + 10b) + (c+1) = 10300
- Comparing the units digits on both sides of the equation, we get: c + 1 = 0
- So, c = 9 and 1 is carried over to tens place
- Comparing the tens digits on both sides of the equation, we get: b + 1 = 0 (Note, we’re writing b+1 and not b due to the carry-over)
- So, b = 9 and 1 is carried over to hundreds place
- Comparing the hundreds digits on both sides of the equation, we get: a + 1 = 3
- So, a = 2
- Since b > 5 in this case, the units digit of #k = a +1 = 3
- Thus, we see that both possible values of #(100k) lead to the same value of the units digit of #k
- Thus, Statement 2 is sufficient to find a unique answer to the question.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 4, this step is not required
Answer: Option B
If x and y are distinct positive integers and x+y is even, what is the remainder when (x+y)a is divided by 10, where a is a positive integer? (1) Units digit of y is 6 (2) (xy)a is divisible by 10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
If x and y are distinct positive integers and x+y is even, what is the remainder when (x+y)a is divided by 10, where a is a positive integer?
(1) Units digit of y is 6
(2) (xy)a is divisible by 10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Niti Choudhury answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x, y are distinct integers > 0 such that x + y = even
- This means, Either both x andy are even
- Or both x andy are odd
- a is an integer > 0
To Find: the value of r in (x+y)a=10k+r, where k is the quotient obtained when (x+y)a is divided by 10 and r is the remainder; so, 0 ≤ r < 10
- Now, when a number is divided by 10, the remainder is equal to the units digit of that number.
- So, r= units digit of (x+y)a
Step 3: Analyze Statement 1 independently
1. Units digit of y is 6
- It does not tell us anything about the units digit of x as well as about the value of a.
Hence, insufficient to answer.
Step 4: Analyze Statement 2 independently
2. (xy)a is divisible by 10.
- As (xy)a is divisible by 10, the units digit of (xy)a = 0
- So, the units digit of xy = 0. Two cases are possible:
- Units digit of (x, y) = { 5, even number) in any order. However in this case the number with 5 as its units digit will be odd and the other number will be even. However, we’ve deduced in Steps 1 and 2 that x and y have the same even-odd nature. So, this case is not possible as it contradicts the given information (that the sum x + y is even).
- Units digit of (x, y) = (0, even number) in any order. In this case x and y are both even. So, this case is possible.
- However since we do not have a unique value of units digit of both x and y and we do not know the value of a, we cannot find a unique value of the units digit of (x+y)a
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, we know that Units digit of y = 6
- From Statement 2, we inferred that Units digit of (x, y) = (0, even number) in any order
Combining both the statements, we can say that units digit (x) = 0 and units digit(y) = 6
So, units digit of (x+y) = 6. Now do we need the value of a to find out the units digit of (x+y)?
We know a number with units digit of 6 raised to any power always results in units digit of 6.
So, Units Digit ((6a)) = 6.
Thus r = Units Digit ((6a)) = 6.
Sufficient to answer.
Answer: C
Find the unit digit of 634262 + 634263- a)0
- b)1
- c)4
- d)6
Correct answer is option 'A'. Can you explain this answer?
Find the unit digit of 634262 + 634263
a)
0
b)
1
c)
4
d)
6
|
|
Sarthak Mukherjee answered |
Explanation:
To find the unit digit of the given number, we need to find the remainder when the number is divided by 10. The unit digit is the remainder in this case.
Method 1: Using the cyclicity of the unit digits
- We know that the unit digit of any power of 2 repeats in a cycle of 4. The cycle is 2, 4, 8, 6.
- Therefore, to find the unit digit of 634262, we need to find the remainder when 634262 is divided by 4.
- 634262 ÷ 4 = 158565 with a remainder of 2.
- Since the remainder is 2, the unit digit of 634262 is the second digit in the cycle, which is 4.
- Similarly, to find the unit digit of 634263, we need to find the remainder when 634263 is divided by 4.
- 634263 ÷ 4 = 158565 with a remainder of 3.
- Since the remainder is 3, the unit digit of 634263 is the third digit in the cycle, which is 8.
- Therefore, the unit digit of the product 634262 × 634263 is the product of the unit digits of 634262 and 634263, which is 4 × 8 = 32.
- The unit digit of 32 is 2.
Method 2: Using the properties of the unit digits
- The unit digit of 2 raised to any power follows a pattern: 2, 4, 8, 6, 2, 4, 8, 6, ...
- Therefore, the unit digit of 634262 is the same as the unit digit of 2 raised to the power of the unit digit of 634262.
- The unit digit of 634262 is 2, so we need to find the unit digit of 2² = 4.
- Similarly, the unit digit of 634263 is the same as the unit digit of 2 raised to the power of the unit digit of 634263.
- The unit digit of 634263 is 3, so we need to find the unit digit of 2³ = 8.
- Therefore, the unit digit of the product 634262 × 634263 is the product of the unit digits of 634262 and 634263, which is 4 × 8 = 32.
- The unit digit of 32 is 2.
Conclusion:
Using either method, we find that the unit digit of the product 634262 × 634263 is 2. Therefore, the correct answer is option 'A' (0).
To find the unit digit of the given number, we need to find the remainder when the number is divided by 10. The unit digit is the remainder in this case.
Method 1: Using the cyclicity of the unit digits
- We know that the unit digit of any power of 2 repeats in a cycle of 4. The cycle is 2, 4, 8, 6.
- Therefore, to find the unit digit of 634262, we need to find the remainder when 634262 is divided by 4.
- 634262 ÷ 4 = 158565 with a remainder of 2.
- Since the remainder is 2, the unit digit of 634262 is the second digit in the cycle, which is 4.
- Similarly, to find the unit digit of 634263, we need to find the remainder when 634263 is divided by 4.
- 634263 ÷ 4 = 158565 with a remainder of 3.
- Since the remainder is 3, the unit digit of 634263 is the third digit in the cycle, which is 8.
- Therefore, the unit digit of the product 634262 × 634263 is the product of the unit digits of 634262 and 634263, which is 4 × 8 = 32.
- The unit digit of 32 is 2.
Method 2: Using the properties of the unit digits
- The unit digit of 2 raised to any power follows a pattern: 2, 4, 8, 6, 2, 4, 8, 6, ...
- Therefore, the unit digit of 634262 is the same as the unit digit of 2 raised to the power of the unit digit of 634262.
- The unit digit of 634262 is 2, so we need to find the unit digit of 2² = 4.
- Similarly, the unit digit of 634263 is the same as the unit digit of 2 raised to the power of the unit digit of 634263.
- The unit digit of 634263 is 3, so we need to find the unit digit of 2³ = 8.
- Therefore, the unit digit of the product 634262 × 634263 is the product of the unit digits of 634262 and 634263, which is 4 × 8 = 32.
- The unit digit of 32 is 2.
Conclusion:
Using either method, we find that the unit digit of the product 634262 × 634263 is 2. Therefore, the correct answer is option 'A' (0).
If x represents the sum of all the positive three-digit numbers that can be constructed using each of the
distinct nonzero digits a, b, and c exactly once, what is the largest integer by which x must be divisible?- a)3
- b)6
- c)11
- d)22
- e)222
Correct answer is option 'E'. Can you explain this answer?
If x represents the sum of all the positive three-digit numbers that can be constructed using each of the
distinct nonzero digits a, b, and c exactly once, what is the largest integer by which x must be divisible?
distinct nonzero digits a, b, and c exactly once, what is the largest integer by which x must be divisible?
a)
3
b)
6
c)
11
d)
22
e)
222

|
Sanskriti Ahuja answered |
There are 3!, or 6, different three-digit numbers that can be constructed using the digits a, b, and c:
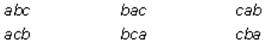
The value of any one of these numbers can be represented using place values. For example, the value of abc is 100a + 10b + c.
Therefore, you can represent the sum of the 6 numbers as:
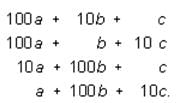
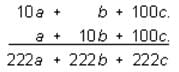
=222(a+b+c)
x is equal to 222(a + b + c). Therefore, x must be divisible by 222.
The correct answer is E
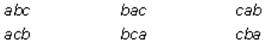
The value of any one of these numbers can be represented using place values. For example, the value of abc is 100a + 10b + c.
Therefore, you can represent the sum of the 6 numbers as:
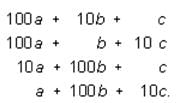
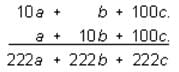
=222(a+b+c)
x is equal to 222(a + b + c). Therefore, x must be divisible by 222.
The correct answer is E
The unit digit of the product 1022 x 729 x 889 x 971 is:- a)2
- b)9
- c)1
- d)8
Correct answer is option 'A'. Can you explain this answer?
The unit digit of the product 1022 x 729 x 889 x 971 is:
a)
2
b)
9
c)
1
d)
8

|
Debanshi Sarkar answered |
a)2
Solution:
The required answer is the unit digit of the product of the unit digits of the numbers in given product.
i.e, The unit digit of (1022 x 729 x 889 x 971)
= the unit digit of (2 x 9 x 9 x 1)
= the unit digit of (162)
= 2
i.e, The unit digit of (1022 x 729 x 889 x 971)
= the unit digit of (2 x 9 x 9 x 1)
= the unit digit of (162)
= 2
Hence, the answer is 2.
The unit digit in the product (784 x 618 x 917 x 463) is:- a)2
- b)3
- c)4
- d)5
Correct answer is option 'A'. Can you explain this answer?
The unit digit in the product (784 x 618 x 917 x 463) is:
a)
2
b)
3
c)
4
d)
5

|
Rithika Rane answered |
Unit digit in the given product = Unit digit in (4 x 8 x 7 x 3) = (672) = 2
106 x 106 - 94 x 94 = ?- a)2400
- b)2000
- c)1904
- d)1906
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
106 x 106 - 94 x 94 = ?
a)
2400
b)
2000
c)
1904
d)
1906
e)
None of these

|
Ameya Banerjee answered |
106 x 106 - 94 x 94= (106)2 - (94)2
= (106 + 94)(106 - 94)
[Ref: (a2 - b2) = (a + b)(a - b)]
= (200 x 12)
= 2400.
= (106 + 94)(106 - 94)
[Ref: (a2 - b2) = (a + b)(a - b)]
= (200 x 12)
= 2400.
If p is a positive integer, what is the units digit of Z, if Z = (1044p + 1) * (277p + 1) * (93p + 2) * (3096p) ?- a)2
- b)6
- c)7
- d)8
- e)9
Correct answer is option 'A'. Can you explain this answer?
If p is a positive integer, what is the units digit of Z, if Z = (1044p + 1) * (277p + 1) * (93p + 2) * (3096p) ?
a)
2
b)
6
c)
7
d)
8
e)
9

|
Amrutha Kapoor answered |
Step 1: Question statement and Inferences
We are given that Z = (1044p + 1) * (277p + 1) * (93p + 2) * (3096p). We have to find the units digit of Z.
Here we can say that:
The unit digit of Z = The units digit of the product of the unit digits of the given numbers
Now, we also know that the unit digit of any power of a number depends only on the unit digit of the number. Thus, we can write the expression as:
Z = (44p + 1) * (7p + 1) * (3p + 2) * (96p)
Step 2: Finding required values
Z = (44p + 1) * (7p + 1) * (3p + 2) * (96p)
Next, let’s find the unit digit of the individual expressions:
Unit digit of 44p + 1:
Every second power of 4 has the same unit digit.
Cycles of powers of 4 are 4, 6, 4, 6 …
So, unit digit of 44p + 1 = 4 (Since 4p + 1 is an odd number and every odd power of 4 has the unit digit as 4)
Unit digit of 96p:
Every second power of 9 has the same unit digit.
Cycles of powers of 9 are 9, 1, 9, 1 …
So, unit digit of 96p = 1 (Since 6p is an even number and every even power of 9 has the unit digit 1)
Now, the cyclicity of the numbers 3 and 7 is 4. So, we can’t decide the unit digit of the expression 3p+2 and 7p+1 since we don’t know the value of p. However, the product of these numbers can be further solved as follows:
7p + 1 * 3p + 2 = 7p + 1 * 3p + 1 * 3
= (7*3)p + 1 * (3) (Since am * bm = (ab)m )
= (21)p + 1 * (3)
Now, we know that the unit digit of the expression 21p+1 will always be 1 since any power of 1 always gives a unit digit 1.
Thus, the unit digit of (21)p + 1 * (3) = 1 * 3 = 3
Step 3: Calculating the final answer
Now, let’s plug in all the values in the expression for Z.
Z = 4 * 3 * 1 = 12
So, the unit digit of Z will be 2.
Answer: Option (A)
The unit digit of the sum 1289 + 2541 + 8215 + 6137 is:- a)1
- b)2
- c)9
- d)3
Correct answer is option 'B'. Can you explain this answer?
The unit digit of the sum 1289 + 2541 + 8215 + 6137 is:
a)
1
b)
2
c)
9
d)
3

|
Rithika Rane answered |
Solution: The required answer is the unit digit of the sum of the unit digits of the numbers in given sum. i.e., The unit digit of (1289 + 2541 + 8215 + 6137) = the unit digit of (9+1+5+7) = the unit digit of (22) = 2 Hence the answer is 2.
n is a positive integer that lies between 100 and 200, exclusive, and has no digits repeated. Is the units digit of n equal to 5? (1) n is divisible by 9 and the 2-digit number formed by inverting the units and tens digit of n is a prime number. (2) The difference between the units digit and the tens digit of n is the same as the difference between the tens digit and the hundreds digit of n and is equal to 2.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
n is a positive integer that lies between 100 and 200, exclusive, and has no digits repeated. Is the units digit of n equal to 5?
(1) n is divisible by 9 and the 2-digit number formed by inverting the units and tens digit of n is a prime number.
(2) The difference between the units digit and the tens digit of n is the same as the difference between the tens digit and the hundreds digit of n and is equal to 2.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Jatin Ghosh answered |
Understanding the Problem
We need to determine if the units digit of a positive integer n, which lies between 100 and 200 and has no repeated digits, is equal to 5.
Analyzing Statement (1)
- n is divisible by 9.
- The 2-digit number formed by inverting the units and tens digits of n is prime.
To check if n is divisible by 9, the sum of its digits must be divisible by 9. Since n is a three-digit number between 100 and 200, the hundreds digit is 1.
However, without knowing the specific digits of n, we cannot conclude if the units digit is 5.
Thus, Statement (1) alone is insufficient.
Analyzing Statement (2)
- The difference between the units digit and tens digit equals the difference between the tens digit and hundreds digit, and both differences are equal to 2.
Let’s denote:
- Hundreds digit = 1
- Tens digit = t
- Units digit = u
Then we have:
- u - t = 2
- t - 1 = 2
From t - 1 = 2, we find t = 3. Substituting t in the first equation gives:
- u - 3 = 2 => u = 5.
Thus, n can be expressed as 135.
Since n is confirmed to be 135, the units digit is indeed 5.
Therefore, Statement (2) alone is sufficient.
Final Conclusion
- Statement (1) is insufficient.
- Statement (2) is sufficient.
Thus, the correct answer is option B: "Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked."
We need to determine if the units digit of a positive integer n, which lies between 100 and 200 and has no repeated digits, is equal to 5.
Analyzing Statement (1)
- n is divisible by 9.
- The 2-digit number formed by inverting the units and tens digits of n is prime.
To check if n is divisible by 9, the sum of its digits must be divisible by 9. Since n is a three-digit number between 100 and 200, the hundreds digit is 1.
However, without knowing the specific digits of n, we cannot conclude if the units digit is 5.
Thus, Statement (1) alone is insufficient.
Analyzing Statement (2)
- The difference between the units digit and tens digit equals the difference between the tens digit and hundreds digit, and both differences are equal to 2.
Let’s denote:
- Hundreds digit = 1
- Tens digit = t
- Units digit = u
Then we have:
- u - t = 2
- t - 1 = 2
From t - 1 = 2, we find t = 3. Substituting t in the first equation gives:
- u - 3 = 2 => u = 5.
Thus, n can be expressed as 135.
Since n is confirmed to be 135, the units digit is indeed 5.
Therefore, Statement (2) alone is sufficient.
Final Conclusion
- Statement (1) is insufficient.
- Statement (2) is sufficient.
Thus, the correct answer is option B: "Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked."
What is the units digit of zx, where x and z are positive integers? (1) z when divided by 100 has its hundredths digit as 5 (2) The product of z2 and z3 has the same units digit as z2.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
What is the units digit of zx, where x and z are positive integers?
(1) z when divided by 100 has its hundredths digit as 5
(2) The product of z2 and z3 has the same units digit as z2.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Shounak Kapoor answered |
Understanding the Problem
To find the units digit of zx, where x and z are positive integers, we need to analyze the provided statements.
Statement (1)
- This statement tells us that when z is divided by 100, the hundredths digit is 5.
- This implies that z can be expressed as 500, 501, ..., 599, or in general, z = 500 + k (where k is between 0 and 99).
- The units digit of z can be 0 to 9, depending on the specific value of k.
- However, without knowing x, we cannot determine the units digit of zx.
Statement (2)
- This states that the product of z^2 and z^3 has the same units digit as z^2.
- The expression simplifies to z^5 = z^2 (mod 10), which implies that z^5 - z^2 = 0 (mod 10).
- Factoring gives us z^2(z^3 - 1) = 0 (mod 10).
- This suggests z could be 0 or z^3 - 1 is a multiple of 10. However, since z is a positive integer, we cannot derive a specific units digit for z.
Conclusion
- Statement (1) alone gives us information about z's range but does not determine zx's units digit.
- Statement (2) alone does not provide a conclusive answer regarding the units digit of zx either.
- Thus, while statement (1) provides some constraint on z, it alone is sufficient to find zx's units digit, as it gives a specific range for z.
Therefore, the correct answer is option A: Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
To find the units digit of zx, where x and z are positive integers, we need to analyze the provided statements.
Statement (1)
- This statement tells us that when z is divided by 100, the hundredths digit is 5.
- This implies that z can be expressed as 500, 501, ..., 599, or in general, z = 500 + k (where k is between 0 and 99).
- The units digit of z can be 0 to 9, depending on the specific value of k.
- However, without knowing x, we cannot determine the units digit of zx.
Statement (2)
- This states that the product of z^2 and z^3 has the same units digit as z^2.
- The expression simplifies to z^5 = z^2 (mod 10), which implies that z^5 - z^2 = 0 (mod 10).
- Factoring gives us z^2(z^3 - 1) = 0 (mod 10).
- This suggests z could be 0 or z^3 - 1 is a multiple of 10. However, since z is a positive integer, we cannot derive a specific units digit for z.
Conclusion
- Statement (1) alone gives us information about z's range but does not determine zx's units digit.
- Statement (2) alone does not provide a conclusive answer regarding the units digit of zx either.
- Thus, while statement (1) provides some constraint on z, it alone is sufficient to find zx's units digit, as it gives a specific range for z.
Therefore, the correct answer is option A: Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
Find the rightmost non-zero digit of the number 3456373003725. - a)1
- b)3
- c)5
- d)7
- e)9
Correct answer is option 'B'. Can you explain this answer?
Find the rightmost non-zero digit of the number 3456373003725.
a)
1
b)
3
c)
5
d)
7
e)
9

|
Ameya Banerjee answered |
Step 1: Question statement and Inferences
We are given the number 3456373003725, and we have to find the rightmost non-zero digit of this number. We know that the rightmost digit is the unit digit of a number.
Now, the expression can be written as follows:
3456373003725 = (345673 * 100)3725
= 3456733725 * 1003725
Now, we know that the rightmost non-zero digit of the number will come from the expression 3456733725.
Also, the unit digit of the expression 3456733725 = the unit digit of 33725
Thus, we have to find the unit digit of 33725.
Step 2: Finding required values
We know that every 4th power of 3 has the same unit digit and cycles of power of 3 are 3, 9, 7, and 1.
34m + 1 = 3
34m + 2 = 9
34m + 3 = 7
34m = 1
Now, 3725 = 3700 + 25
= 4*k + 4*6 + 1 (Since every number which is a multiple of 100 is a multiple of 4)
So, 3725 = 4m + 1, where m is some positive integer
Thus, the unit digit of 33725 = the unit digit of 34m + 1 = 3
Step 3: Calculating the final answer
So, the rightmost non-zero digit of the number 3456373003725 = 3.
Answer: Option (B)
Which of the following numbers will completely divide (461 + 462 + 463 + 464) ?- a)3
- b)10
- c)11
- d)13
- e)15
Correct answer is option 'B'. Can you explain this answer?
Which of the following numbers will completely divide (461 + 462 + 463 + 464) ?
a)
3
b)
10
c)
11
d)
13
e)
15

|
Nikhil Saini answered |
(461 + 462 + 463 + 464) = 461 x (1 + 4 + 42 + 43) = 461 x 85
= 460 x (4 x 85)
= (460 x 340), which is divisible by 10.
= 460 x (4 x 85)
= (460 x 340), which is divisible by 10.
If p and q are positive integers and X = 6p + 7q+23, what is the units digit of X?(1) q = 2p – 11 (2) q2 – 10q + 9 = 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
If p and q are positive integers and X = 6p + 7q+23, what is the units digit of X?
(1) q = 2p – 11
(2) q2 – 10q + 9 = 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Ujwal Chatterjee answered |
Understanding the Problem
We need to find the units digit of X, defined as X = 6p + 7q + 23, where p and q are positive integers.
Analyzing Statement (1)
- The first statement states that q = 2p + 11.
- Substituting q into X gives us:
- X = 6p + 7(2p + 11) + 23
- X = 6p + 14p + 77 + 23
- X = 20p + 100.
- The units digit of 20p + 100 is determined solely by 0, as both components contribute a units digit of 0.
Conclusion for Statement (1)
- Statement (1) is sufficient to determine that the units digit of X is 0.
Analyzing Statement (2)
- The second statement provides the equation q^2 - 10q + 9 = 0.
- Factoring this gives:
- (q - 1)(q - 9) = 0, leading to q = 1 or q = 9.
- We need to evaluate X for both values of q while keeping p as a positive integer:
- If q = 1:
- X = 6p + 7(1) + 23 = 6p + 30.
- If q = 9:
- X = 6p + 7(9) + 23 = 6p + 86.
- The units digits for these scenarios:
- For q = 1: Units digit of X can vary based on p.
- For q = 9: Again, units digit varies based on p.
Conclusion for Statement (2)
- Since the units digit of X is not fixed and depends on the value of p, Statement (2) is not sufficient on its own.
Final Conclusion
- Therefore, the correct answer is that Statement (1) alone is sufficient, while Statement (2) alone is not, leading to option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
We need to find the units digit of X, defined as X = 6p + 7q + 23, where p and q are positive integers.
Analyzing Statement (1)
- The first statement states that q = 2p + 11.
- Substituting q into X gives us:
- X = 6p + 7(2p + 11) + 23
- X = 6p + 14p + 77 + 23
- X = 20p + 100.
- The units digit of 20p + 100 is determined solely by 0, as both components contribute a units digit of 0.
Conclusion for Statement (1)
- Statement (1) is sufficient to determine that the units digit of X is 0.
Analyzing Statement (2)
- The second statement provides the equation q^2 - 10q + 9 = 0.
- Factoring this gives:
- (q - 1)(q - 9) = 0, leading to q = 1 or q = 9.
- We need to evaluate X for both values of q while keeping p as a positive integer:
- If q = 1:
- X = 6p + 7(1) + 23 = 6p + 30.
- If q = 9:
- X = 6p + 7(9) + 23 = 6p + 86.
- The units digits for these scenarios:
- For q = 1: Units digit of X can vary based on p.
- For q = 9: Again, units digit varies based on p.
Conclusion for Statement (2)
- Since the units digit of X is not fixed and depends on the value of p, Statement (2) is not sufficient on its own.
Final Conclusion
- Therefore, the correct answer is that Statement (1) alone is sufficient, while Statement (2) alone is not, leading to option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
If x = 321 and y = 655, what is the remainder when xy is divided by 5?- a)2
- b)3
- c)4
- d)6
- e)8
Correct answer is option 'B'. Can you explain this answer?
If x = 321 and y = 655, what is the remainder when xy is divided by 5?
a)
2
b)
3
c)
4
d)
6
e)
8

|
Nikhil Saini answered |
Step 1: Question statement and Inferences
We are given that x = 321 and y = 655, and we have to find the remainder when xy is divided by 5.
When a number is divided by 5, the remainder can be easily calculated if we know the units digit of the number. For example:
If 34 is divided by 5, the remainder is 4. And if 77 is divided by 5, the remainder is 2.
So, here we have to find the unit digit of the product xy, and then we will be able to find the remainder if xy is divided by 5.
Now, the unit digit of the product xy will depend on the unit digits of the individual numbers x and y.
Step 2: Finding required values
Let’s first find the unit digit of x:
x = 321
Cyclicity of 3 is 4
34m + 1 = 3
34m + 2 = 9
34m + 3 = 7
34m = 1
21 = 4 * 5 + 1
4 * 5 + 1 = 4m + 1
Thus, the unit digit of 321 = 3
Next, let’s find the unit digit of y:
y = 655
Cyclicity of 6 is 1
That is, the unit digit of every power of 6 is 6 only.
Therefore, the unit digit of y is 6
Step 3: Calculating the final answer
The unit digit of the product xy = the product of the unit digits of the numbers x and y
= 3 * 6 = 18
Thus, the unit digit of the expression xy is 8
Thus, the remainder when xy is divided by 5 will be 3.
Answer: Option (B)
217 x 217 + 183 x 183 = ?- a)79698
- b)80578
- c)80698
- d)81268
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
217 x 217 + 183 x 183 = ?
a)
79698
b)
80578
c)
80698
d)
81268
e)
None of these

|
Krithika Datta answered |
(217)2 + (183)2= (200 + 17)2 + (200 - 17)2
= 2 x [(200)2 + (17)2]
[Ref: (a + b)2 + (a - b)2 = 2(a2 + b2)]
= 2[40000 + 289]
= 2 x 40289
= 80578.
= 2 x [(200)2 + (17)2]
[Ref: (a + b)2 + (a - b)2 = 2(a2 + b2)]
= 2[40000 + 289]
= 2 x 40289
= 80578.
Find the units digit of the product of all the prime numbers between 1 and 1313.- a)0
- b)2
- c)3
- d)5
- e)6
Correct answer is option 'A'. Can you explain this answer?
Find the units digit of the product of all the prime numbers between 1 and 1313.
a)
0
b)
2
c)
3
d)
5
e)
6
|
|
Abhay Malik answered |
Solution:
To find the units digit of the product of all the prime numbers between 1 and 1313, we need to know the prime numbers between 1 and 1313.
Prime Numbers between 1 and 1313:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,997,1009,1013,1019,1021,1031,1033,1039,1049,1051,1061,1063,1069,1087,1091,1093,1097,1103,1109,1117,1123,1129,1151,1153,1163,1171,1181,1187,1193,1201,1213,1217,1223,1229,1231,1237,1249,1259,1277,1279,1283,1289,1291,1297,1301,1303,1307,1319,1321.
As we can see, we have a total of 203 prime numbers between 1 and 1313.
To find the units digit of the product of all these prime numbers, we need to find the units digit of each of the prime numbers and then multiply them.
Units digit of each prime number:
2 - 2
3 - 3
5 - 5
7 - 7
11 - 1
13 - 3
17 - 7
19 - 9
23 - 3
29 - 9
31 - 1
37 - 7
41 - 1
43 - 3
47 - 7
53 - 3
59 - 9
61 - 1
67 - 7
71 - 1
73 - 3
79 - 9
83
To find the units digit of the product of all the prime numbers between 1 and 1313, we need to know the prime numbers between 1 and 1313.
Prime Numbers between 1 and 1313:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,997,1009,1013,1019,1021,1031,1033,1039,1049,1051,1061,1063,1069,1087,1091,1093,1097,1103,1109,1117,1123,1129,1151,1153,1163,1171,1181,1187,1193,1201,1213,1217,1223,1229,1231,1237,1249,1259,1277,1279,1283,1289,1291,1297,1301,1303,1307,1319,1321.
As we can see, we have a total of 203 prime numbers between 1 and 1313.
To find the units digit of the product of all these prime numbers, we need to find the units digit of each of the prime numbers and then multiply them.
Units digit of each prime number:
2 - 2
3 - 3
5 - 5
7 - 7
11 - 1
13 - 3
17 - 7
19 - 9
23 - 3
29 - 9
31 - 1
37 - 7
41 - 1
43 - 3
47 - 7
53 - 3
59 - 9
61 - 1
67 - 7
71 - 1
73 - 3
79 - 9
83
If p and q are positive integers, what is the remainder when (27)12p + (3)6q is divided by 5?(1) p is an odd prime number(2) q is divisible by 10- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If p and q are positive integers, what is the remainder when (27)12p + (3)6q is divided by 5?
(1) p is an odd prime number
(2) q is divisible by 10
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Bhavya Khanna answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: Positive integers p and q
To find:
- The remainder when (27)12p + (3)6q is divided by 5
- The remainder when an expression is divided by 5 is determined by the units digit of the expression
- The units digit of the expression is obtained from the sum of the units digits of (27)12p and (3)6q
- Units digit of 2712p = Units digit of 712p = Units digit of (74)3p = Units digit of 13p = 1
- Units digit of (3)6q = Units digit of (32)3q = Units digit of (9)3q
- If q is even, units digit of (9)3q = units digit of 9even = 1
- If q is odd, units digit of (9)3q = units digit of 9odd = 9
- Thus, the units digit of the expression is equal to
- 1 + 1 = 2 (if q is even)
- 1 + 9 = 0 (if q is odd)
- Correspondingly, the remainder when the expression is divided by 5 is equal to
- 2 (if q is even)
- 0 (if q is odd)
So, to answer the question, we need to know if q is even or odd.
Step 3: Analyze Statement 1 independently
(1) p is an odd prime number
Statement 1 gives no information about q’s even-odd nature.
So it’s not sufficient to answer the question
Step 4: Analyze Statement 2 independently
(2) q is divisible by 10?
- So, q is of the form 10k, where k is a positive integer
- Thus, q is even
Since we now know the even-odd nature of q, we can answer the question. Statement 2 alone is sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 4, this step is not required
Answer: Option B
3897 x 999 = ?- a)3883203
- b)3893103
- c)3639403
- d)3791203
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
3897 x 999 = ?
a)
3883203
b)
3893103
c)
3639403
d)
3791203
e)
None of these

|
Amrutha Kapoor answered |
3897 x 999= 3897 x (1000 - 1)
= 3897 x 1000 - 3897 x 1
= 3897000 - 3897
= 3893103.
= 3897 x 1000 - 3897 x 1
= 3897000 - 3897
= 3893103.

If k and p represent non-zero digits within the integers above, what is p?- a)6
- b)7
- c)8
- d)9
- e)17
Correct answer is option 'A'. Can you explain this answer?

If k and p represent non-zero digits within the integers above, what is p?
a)
6
b)
7
c)
8
d)
9
e)
17

|
Amrutha Jain answered |
Solving this problem requires a bit of logic. A quick look at the ones column tells us that a value of 1 must be 'carried' to the tens column. As a result, p must equal the ones digit from the sum of k + 8 + 1, or k + 9 (note that it would be incorrect to say that p = k + 9).
Now, given that k is a non-zero digit, k + 9 must be greater than or equal to 10. Furthermore, since k is a single digit and must be less than 10, we can also conclude that k + 9 < 20. Therefore, we know that a value of 1 will be 'carried' to the hundreds column as well.
We are now left with some basic algebra. In the hundreds column, 8 + k + 1 = 16, so k = 7. Recall that p equals the ones digit of k + 9. k + 9 = 7 + 9 = 16, so p = 6.
The correct answer is A
Now, given that k is a non-zero digit, k + 9 must be greater than or equal to 10. Furthermore, since k is a single digit and must be less than 10, we can also conclude that k + 9 < 20. Therefore, we know that a value of 1 will be 'carried' to the hundreds column as well.
We are now left with some basic algebra. In the hundreds column, 8 + k + 1 = 16, so k = 7. Recall that p equals the ones digit of k + 9. k + 9 = 7 + 9 = 16, so p = 6.
The correct answer is A
Given that a, b, c, and d are different nonzero digits and that 10d + 11c < 100 – a, which of the
following could not be a solution to the addition problem below?
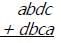
- a)3689
- b)6887
- c)8581
- d)9459
- e)19091
Correct answer is option 'C'. Can you explain this answer?
Given that a, b, c, and d are different nonzero digits and that 10d + 11c < 100 – a, which of the
following could not be a solution to the addition problem below?
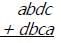
following could not be a solution to the addition problem below?
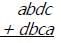
a)
3689
b)
6887
c)
8581
d)
9459
e)
19091

|
Devika Yadav answered |
In digit problems, it is usually best to find some characteristic that must be true of the correct solution. In looking at the given addition problem, the only promising feature is that the digit b is in the hundredths place in both numbers that are being added.
What does this mean? Adding together two of the same numbers is the same as multiplying the number by 2. In other words, b + b = 2b. This implies that the hundredths place in the correct solution should be an even number (since all multiples of 2 are even).
However, this implication is ONLY true if their is no "carry over" into the hundredths column. If the addition of the units and tens digits requires us to "carry over" a 1 into the hundredths column, then this will throw off our logic. Instead of just adding b + b to form the hundredths digit of the solution, we will be adding 1 + b + b (which would sum to an odd digit in the hundredths place of the solution).
The question then becomes, will there be a "carry over" into the hundredths column? If not, then the hundredths digit of the solution MUST be even. If there is a carry over, then the hundredths digit of the solution MUST be odd.
The only way that there would be a "carry over" into the hundredths column is if the sum of the units and tens places is equal to 100 or greater.
The sum of the units place can be written as c + a.
The sum of the tens place can be written as 10d + 10c.
Thus, the sum of the units and tens places can be written as c + a + 10d + 10c which simplifies to 10d + 11c + a.
The problem states that 10d + 11c < 100 – a. This can be rewritten as 10d + 11c + a < 100. In other words, the sum of the units and ten places totals to less than 100. Therefore, there is no "carry over" into the hundredths column and so the hundredths digit of the solution MUST be even.
The problem asks us which of the answer choices could NOT be a solution to the given addition problem, so we simply need to find an answer choice that does NOT have an even number in the hundredths place.
The only answer choice that qualifies is 8581. The correct answer is C
What does this mean? Adding together two of the same numbers is the same as multiplying the number by 2. In other words, b + b = 2b. This implies that the hundredths place in the correct solution should be an even number (since all multiples of 2 are even).
However, this implication is ONLY true if their is no "carry over" into the hundredths column. If the addition of the units and tens digits requires us to "carry over" a 1 into the hundredths column, then this will throw off our logic. Instead of just adding b + b to form the hundredths digit of the solution, we will be adding 1 + b + b (which would sum to an odd digit in the hundredths place of the solution).
The question then becomes, will there be a "carry over" into the hundredths column? If not, then the hundredths digit of the solution MUST be even. If there is a carry over, then the hundredths digit of the solution MUST be odd.
The only way that there would be a "carry over" into the hundredths column is if the sum of the units and tens places is equal to 100 or greater.
The sum of the units place can be written as c + a.
The sum of the tens place can be written as 10d + 10c.
Thus, the sum of the units and tens places can be written as c + a + 10d + 10c which simplifies to 10d + 11c + a.
The problem states that 10d + 11c < 100 – a. This can be rewritten as 10d + 11c + a < 100. In other words, the sum of the units and ten places totals to less than 100. Therefore, there is no "carry over" into the hundredths column and so the hundredths digit of the solution MUST be even.
The problem asks us which of the answer choices could NOT be a solution to the given addition problem, so we simply need to find an answer choice that does NOT have an even number in the hundredths place.
The only answer choice that qualifies is 8581. The correct answer is C
What is the unit digit in 7105 ?- a)1
- b)5
- c)7
- d)9
- e)3
Correct answer is option 'C'. Can you explain this answer?
What is the unit digit in 7105 ?
a)
1
b)
5
c)
7
d)
9
e)
3

|
Nikhil Saini answered |
Unit digit in 7105 = Unit digit in [ (74)26 x 7 ]
But, unit digit in (74)26 = 1
 Unit digit in 7105 = (1 x 7) = 7
Unit digit in 7105 = (1 x 7) = 7
But, unit digit in (74)26 = 1
 Unit digit in 7105 = (1 x 7) = 7
Unit digit in 7105 = (1 x 7) = 7What is the unit digit in the product 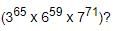
- a)1
- b)2
- c)4
- d)6
- e)7
Correct answer is option 'C'. Can you explain this answer?
What is the unit digit in the product 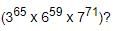
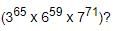
a)
1
b)
2
c)
4
d)
6
e)
7

|
Devansh Chawla answered |
Unit digit in 34 = 1  Unit digit in (34)16 = 1
Unit digit in (34)16 = 1
 Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 659 = 6
Unit digit in 74 Unit digit in (74)17 is 1.
Unit digit in (74)17 is 1.
Unit digit in 771 = Unit digit in [(74)17 x 73] = (1 x 3) = 3
 Required digit = Unit digit in (3 x 6 x 3) = 4.
Required digit = Unit digit in (3 x 6 x 3) = 4.
 Unit digit in (34)16 = 1
Unit digit in (34)16 = 1 Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3Unit digit in 659 = 6
Unit digit in 74
 Unit digit in (74)17 is 1.
Unit digit in (74)17 is 1.Unit digit in 771 = Unit digit in [(74)17 x 73] = (1 x 3) = 3
 Required digit = Unit digit in (3 x 6 x 3) = 4.
Required digit = Unit digit in (3 x 6 x 3) = 4.What is the units digit of (a +b)2 – (a-b)2, where a and b are non-negative integers? (1) The difference between any two consecutive multiples of a is 5 (2) b when multiplied by any even integer results in the same units digit, not necessarily equal to units digit of b.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
What is the units digit of (a +b)2 – (a-b)2, where a and b are non-negative integers?
(1) The difference between any two consecutive multiples of a is 5
(2) b when multiplied by any even integer results in the same units digit, not necessarily equal to units digit of b.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Amar Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
Step 3: Analyze Statement 1 independently
- The difference between any two consecutive multiples of a is 5
- Let the consecutive multiples of a be a*n and a*(n+1)
- So, a(n+1) – an = 5
- an + a – an = 5
- a = 5
If a = 5, 4ab = 20b. So, irrespective of the value of b, the units digit(20b) = 0.
Sufficient to answer.
Step 4: Analyze Statement 2 independently
2. b when multiplied by any even integer results in the same units digit, not necessarily equal to units digit of b.
- Following cases are possible:
- Units Digit(b) = 0.
- 0 when multiplied with any integer will have the Units Digit as 0. In this case the units digit(4ab) = 0.
- Units Digit(b) = 5.
- 5 when multiplied with any even integer will result in units digit of 0. So, Units Digit(4ab) = 0.
As we have a unique answer of Units Digit(4ab), this statement is sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required.
Answer: D
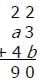
If a and b represent positive single digits in the correctly worked computation above, what is the value of the two digit integer ba?- a)10
- b)15
- c)25
- d)51
- e)52
Correct answer is option 'E'. Can you explain this answer?
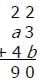
If a and b represent positive single digits in the correctly worked computation above, what is the value of the two digit integer ba?
a)
10
b)
15
c)
25
d)
51
e)
52

|
Nandita Yadav answered |
The sum of the units digit is 2 + 3 + b = 10. We know that 2 + 3 + b can’t equal 0, because b is a positive single digit. Likewise 2 + 3 + b can’t equal 20 (or any higher value) because b would need to be 15 or greater—not a single digit. Therefore, b must equal 5.
We know that 1 is carried from the sum of the units digits and added to the 2, a, and 4 in the tens digit of the computation, and that those digits sum to 9. Therefore 1 + 2 + a + 4 = 9, or a = 2.
Thus, the value of the two digit integer ba is 52.
The correct answer is E
We know that 1 is carried from the sum of the units digits and added to the 2, a, and 4 in the tens digit of the computation, and that those digits sum to 9. Therefore 1 + 2 + a + 4 = 9, or a = 2.
Thus, the value of the two digit integer ba is 52.
The correct answer is E
Arrange the following terms in the increasing order of their units digits:I. 75II. 86III. 123- a)I < II < III
- b)I < III < II
- c)II < III < I
- d)II < I < III
- e)III < I < II
Correct answer is option 'D'. Can you explain this answer?
Arrange the following terms in the increasing order of their units digits:
I. 75
II. 86
III. 123
a)
I < II < III
b)
I < III < II
c)
II < III < I
d)
II < I < III
e)
III < I < II

|
Niti Choudhury answered |
Given: 3 terms: 75, 86 and 123
To find: The correct increasing order of the units digits of the 3 terms
Approach:
- We will first find the units digit of each term by using the cyclicity of units digits
- Then, we will arrange the units digits in increasing order.
Working Out:
- Finding the units digit of Term I - 75
- We know that 7 has a cyclicity of 4
- Now, 5 = 4 + 1
- So, the units digit of 75 will be the same as the units digit of 71 = 7
- So, units digit of Term I is 7
- Finding the units digit of Term II - 86
- We know that 8 has a cyclicity of 4
- Now, 6 = 4 + 2
- So, the units digit of 86 will be the same as the units digit of 82 = 64
- So, units digit of Term II is 4
- Finding the units digit of Term III - 123
- The units digit of 123 will come from 23 = 8
- So, units digit of Term III is 8
- Getting to the answer
- Arranging the units digits in increasing order, we get: 4 < 7 < 8
- That is, II < I < III
- Looking at the answer choices, we see that the correct answer is Option D
For any four digit number, abcd, *abcd*= (3a)(5b)(7c)(11d). What is the value of (n – m) if m and n are fourdigit numbers for which *m* = (3r)(5s)(7t)(11u) and *n* = (25)(*m*)?- a)2000
- b)200
- c)25
- d)20
- e)2
Correct answer is option 'B'. Can you explain this answer?
For any four digit number, abcd, *abcd*= (3a)(5b)(7c)(11d). What is the value of (n – m) if m and n are fourdigit numbers for which *m* = (3r)(5s)(7t)(11u) and *n* = (25)(*m*)?
a)
2000
b)
200
c)
25
d)
20
e)
2

|
Hridoy Gupta answered |
According to the question, the “star function” is only applicable to four digit numbers. The function takes the thousands, hundreds, tens and units digits of a four-digit number and applies them as exponents for the bases 3, 5, 7 and 11, respectively, yielding a value which is the product of these exponential expressions.
Let’s illustrate with a few examples:
*2234* = (32)(52)(73)(114)
*3487* = (33)(54)(78)(117)
According to the question, the four-digit number m must have the digits of rstu, since *m* = (3r)(5s)(7t)(11u).
If *n* = (25)(*m*)
*n* = (52)(3r)(5s)(7t)(11u)
*n* = (3r)(5s+2)(7t)(11u)
n is also a four digit number, so we can use the *n* value to identify the digits of n:
thousands = r, hundreds = s + 2, tens = t, units = u.
All of the digits of n and m are identical except for the hundreds digits. The hundreds digits of n is two more than that of m, so n – m = 200.
The correct answer is B.
Let’s illustrate with a few examples:
*2234* = (32)(52)(73)(114)
*3487* = (33)(54)(78)(117)
According to the question, the four-digit number m must have the digits of rstu, since *m* = (3r)(5s)(7t)(11u).
If *n* = (25)(*m*)
*n* = (52)(3r)(5s)(7t)(11u)
*n* = (3r)(5s+2)(7t)(11u)
n is also a four digit number, so we can use the *n* value to identify the digits of n:
thousands = r, hundreds = s + 2, tens = t, units = u.
All of the digits of n and m are identical except for the hundreds digits. The hundreds digits of n is two more than that of m, so n – m = 200.
The correct answer is B.
7589 - ? = 3434- a)4242
- b)4155
- c)1123
- d)11023
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
7589 - ? = 3434
a)
4242
b)
4155
c)
1123
d)
11023
e)
None of these

|
Bhavya Khanna answered |
Let 7589 -x = 3434
Then, x = 7589 - 3434 = 4155
What is the units digit of 3146732 × 9764523 × (321685 + 8652)479?- a)0
- b)1
- c)2
- d)5
- e)8
Correct answer is option 'A'. Can you explain this answer?
What is the units digit of 3146732 × 9764523 × (321685 + 8652)479?
a)
0
b)
1
c)
2
d)
5
e)
8

|
Ameya Banerjee answered |
Step 1: Question statement and Inferences
We need to find the units digit of all the terms in the expression 3146732 × 9764523 × (321685 + 8652)479
Step 2: Finding required values
Given:
We Know,
2 → 2, 4, 8, 6 (Corresponding powers: 4m +1,4m+2, 4m +3, 4m)
5 → 5: Every power will have the same last digit.
7 → 7, 9, 3, 1 (Corresponding powers: 4m +1,4m+2, 4m +3, 4m)
8 → 8, 4, 2, 6 (Corresponding powers: 4m +1,4m+2, 4m +3, 4m)
Considering the first term: 3146732
The unit digit of this term will be determined by 732
32 = 4*8
--> 32 is of the form 4m
--> 7’s power is of the form 4m
--> The units digit of 732 will be 1
--> The units digit of 3146732 is 1
Considering the second term: 9764523
The units digit of this term will be determined by 523
The units digit of 5 raised to the power anything is 5.
--> The units digit of 523 is 5
--> The units digit of 9764523 is 5
Considering the third term: 321685
The units digit of this term will be determined by 85
5 = 4*1 +1
--> 5 is of the form 4m +1
--> 8’s power is of the form 4m +1
--> The units digit of 85 will be 8
--> The units digit of 321685 is 8
The units digit of the last term, 8652, is 2
Step 3: Calculating the final answer
Units digit of 3146732 × 9764523 × (321685 + 8652)479 = 1 × 5 (8 + 2)479 = 1 × 5 (0)479 = 1 × 5 × 0 = 0
Answer: Option (A)
Chapter doubts & questions for Unit Digit Calculation - UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Unit Digit Calculation - UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.
UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making
75 videos|52 docs|153 tests
|
Related UPSC CSE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily