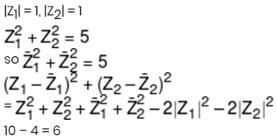All Exams >
JEE >
JEE Main & Advanced Mock Test Series 2025 >
All Questions
All questions of JEE Maths Mocks for JEE Exam
The point on the curve y = x2 which is nearest to (3, 0) is- a)(1, -1)
- b)(-1, 1)
- c)(-1, -1)
- d)(1, 1)
Correct answer is option 'D'. Can you explain this answer?
The point on the curve y = x2 which is nearest to (3, 0) is
a)
(1, -1)
b)
(-1, 1)
c)
(-1, -1)
d)
(1, 1)
|
|
Mayank Kapoor answered |
Given, y = x² and the point (3,0).
To find the point on the curve which is nearest to (3,0), we need to minimize the distance between the two points.
Let the point on the curve be (a, a²).
Distance between (3,0) and (a,a²) is given by:
d = √[(a-3)² + (a²-0)²]
To minimize d, we need to find the value of a which makes d minimum.
Taking the derivative of d w.r.t a and equating it to 0, we get:
(a-3) + 2a(a²-0) = 0
Simplifying, we get:
2a³ - 3a + 3 = 0
This is a cubic equation which can be solved using Cardano's method or by graphing.
Solving the equation, we get three roots: a ≈ -1.32, a ≈ 0.62 and a ≈ 1.06.
Out of these three roots, the point (1,1) is the nearest to (3,0).
Therefore, the correct answer is option D.
To find the point on the curve which is nearest to (3,0), we need to minimize the distance between the two points.
Let the point on the curve be (a, a²).
Distance between (3,0) and (a,a²) is given by:
d = √[(a-3)² + (a²-0)²]
To minimize d, we need to find the value of a which makes d minimum.
Taking the derivative of d w.r.t a and equating it to 0, we get:
(a-3) + 2a(a²-0) = 0
Simplifying, we get:
2a³ - 3a + 3 = 0
This is a cubic equation which can be solved using Cardano's method or by graphing.
Solving the equation, we get three roots: a ≈ -1.32, a ≈ 0.62 and a ≈ 1.06.
Out of these three roots, the point (1,1) is the nearest to (3,0).
Therefore, the correct answer is option D.
If A and B are two events such that
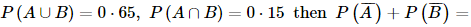
- a)0.6
- b)0.8
- c)1.2
- d)1.4
Correct answer is option 'C'. Can you explain this answer?
If A and B are two events such that
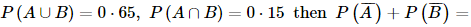
a)
0.6
b)
0.8
c)
1.2
d)
1.4

|
Tarun Kaushik answered |
Correct option is C. 0.8
If A.M. between two numbers is 5 and their G.M. is 4, then their H.M. is- a)16/5
- b)14/5
- c)11/5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If A.M. between two numbers is 5 and their G.M. is 4, then their H.M. is
a)
16/5
b)
14/5
c)
11/5
d)
none of these

|
Akash Shah answered |
If x, y and z respectively represent AM, GM and HM between two numbers a and b, then
y2 = xz
Here x = 5, y = 4
then 16 = 5 x z
z = 16/5
y2 = xz
Here x = 5, y = 4
then 16 = 5 x z
z = 16/5
The orthocentre of the traingle whose vertices are (5, -2), (-1, 2) and (1,4) is- a)(1/5, 14/5)
- b)(14/5, 1/5)
- c)(1/5, 1/5)
- d)(14/5, 14/5)
Correct answer is option 'A'. Can you explain this answer?
The orthocentre of the traingle whose vertices are (5, -2), (-1, 2) and (1,4) is
a)
(1/5, 14/5)
b)
(14/5, 1/5)
c)
(1/5, 1/5)
d)
(14/5, 14/5)
|
|
Shivam Kulkarni answered |
Given: vertices of triangle are (5, -2), (-1, 2) and (1,4)
To find: Orthocentre of the triangle
Concept: The orthocentre of a triangle is the point of intersection of the altitudes of the triangle.
Approach:
1. Find the slope of the line passing through the points (-1,2) and (1,4).
- Slope of line = (y2 - y1) / (x2 - x1) = (4 - 2) / (1 + 1) = 1
2. Find the slope of the line passing through the points (5,-2) and (-1,2).
- Slope of line = (y2 - y1) / (x2 - x1) = (2 - (-2)) / ((-1) - 5) = -1/2
3. Find the equation of the line passing through the point (1,4) with slope -1/2.
- Using point-slope form, y - y1 = m(x - x1), we get
y - 4 = (-1/2)(x - 1)
2y - 8 = -x + 1
x + 2y = 9
4. Find the equation of the line passing through the point (-1,2) with slope 1.
- Using point-slope form, y - y1 = m(x - x1), we get
y - 2 = 1(x - (-1))
y - x = 3
5. Find the point of intersection of the lines obtained in step 3 and step 4.
- Solving the equations x + 2y = 9 and y - x = 3, we get
x = 1/5, y = 14/5
6. Find the equation of the line passing through the point (5,-2) with slope 2.
- Using point-slope form, y - y1 = m(x - x1), we get
y - (-2) = 2(x - 5)
y = 2x - 12
7. Find the point of intersection of the lines obtained in step 6 and step 4.
- Solving the equations y = 2x - 12 and y - x = 3, we get
x = 1/5, y = 14/5
8. Hence, the point of intersection obtained in step 5 and step 7 is the orthocentre of the triangle.
Answer: The orthocentre of the given triangle is (1/5, 14/5) which is option A.
To find: Orthocentre of the triangle
Concept: The orthocentre of a triangle is the point of intersection of the altitudes of the triangle.
Approach:
1. Find the slope of the line passing through the points (-1,2) and (1,4).
- Slope of line = (y2 - y1) / (x2 - x1) = (4 - 2) / (1 + 1) = 1
2. Find the slope of the line passing through the points (5,-2) and (-1,2).
- Slope of line = (y2 - y1) / (x2 - x1) = (2 - (-2)) / ((-1) - 5) = -1/2
3. Find the equation of the line passing through the point (1,4) with slope -1/2.
- Using point-slope form, y - y1 = m(x - x1), we get
y - 4 = (-1/2)(x - 1)
2y - 8 = -x + 1
x + 2y = 9
4. Find the equation of the line passing through the point (-1,2) with slope 1.
- Using point-slope form, y - y1 = m(x - x1), we get
y - 2 = 1(x - (-1))
y - x = 3
5. Find the point of intersection of the lines obtained in step 3 and step 4.
- Solving the equations x + 2y = 9 and y - x = 3, we get
x = 1/5, y = 14/5
6. Find the equation of the line passing through the point (5,-2) with slope 2.
- Using point-slope form, y - y1 = m(x - x1), we get
y - (-2) = 2(x - 5)
y = 2x - 12
7. Find the point of intersection of the lines obtained in step 6 and step 4.
- Solving the equations y = 2x - 12 and y - x = 3, we get
x = 1/5, y = 14/5
8. Hence, the point of intersection obtained in step 5 and step 7 is the orthocentre of the triangle.
Answer: The orthocentre of the given triangle is (1/5, 14/5) which is option A.
If sin y = x sin (a + y), then (dy/dx) =- a)[sin2(a + y)/sin a]
- b)sin (a + y)
- c)sin2 (a + y)
- d)[sin (a + y)/sin a]
Correct answer is option 'A'. Can you explain this answer?
If sin y = x sin (a + y), then (dy/dx) =
a)
[sin2(a + y)/sin a]
b)
sin (a + y)
c)
sin2 (a + y)
d)
[sin (a + y)/sin a]

|
Pavan Kishore answered |
Direct differentiation
x=siny/sin(a+y)
and cosy.sin(a+y)-cos(a+y).siny=sin(a+y-y)
x=siny/sin(a+y)
and cosy.sin(a+y)-cos(a+y).siny=sin(a+y-y)
If a, b are odd integers then number of integral root, of equation x10 + ax9 + b = 0 is equal to :
Correct answer is '0'. Can you explain this answer?
If a, b are odd integers then number of integral root, of equation x10 + ax9 + b = 0 is equal to :
|
|
Neha Joshi answered |
Let P is a root (∈I)
Case-I : p is odd
p10 + ap9 + b ≠ 0
Because LHS odd
Case-II : p is even
p10 + ap9 + b ≠ 0
because, LHs is odd
Case-I : p is odd
p10 + ap9 + b ≠ 0
Because LHS odd
Case-II : p is even
p10 + ap9 + b ≠ 0
because, LHs is odd
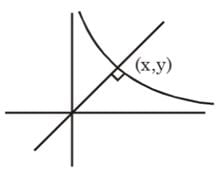
The eccentric angles of the extremities of the latus-rectum intersecting positive x-axis of the ellipse ((x2/a2) + (y2/b2) = 1) are given by- a)tan⁻1(+(ae/b))
- b)tan⁻1(+((be/a))
- c)tan⁻1(+((b/ae))
- d)tan⁻1(+((a/be))
Correct answer is option 'C'. Can you explain this answer?
The eccentric angles of the extremities of the latus-rectum intersecting positive x-axis of the ellipse ((x2/a2) + (y2/b2) = 1) are given by
a)
tan⁻1(+(ae/b))
b)
tan⁻1(+((be/a))
c)
tan⁻1(+((b/ae))
d)
tan⁻1(+((a/be))
|
|
Kirti Reddy answered |
Given: Ellipse equation: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Eccentricity of the ellipse: $e=\sqrt{1-\frac{b^2}{a^2}}$
Latus-rectum of the ellipse: $l= \frac{2b^2}{a}$
Extreme points of latus-rectum: $(\pm\frac{l}{2},\pm b)$
Let $\theta_1$ and $\theta_2$ be the eccentric angles of the extreme points of the latus-rectum with respect to the positive x-axis.
We have to find: $tan(\theta_1+\theta_2)$
To find $\theta_1$ and $\theta_2$, we use the formula:
$tan\theta=\frac{b}{a}\sqrt{\frac{a^2-x^2}{x^2}}$
We get:
$tan\theta_1=\frac{b}{a}\sqrt{\frac{a^2-\frac{l^2}{4}}{\frac{l^2}{4}}}=\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}$
$tan\theta_2=\frac{b}{a}\sqrt{\frac{a^2-\frac{l^2}{4}}{\frac{l^2}{4}}}=-\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}$
Using the formula for tan(A+B), we get:
$tan(\theta_1+\theta_2)=\frac{tan\theta_1+tan\theta_2}{1-tan\theta_1\tan\theta_2}$
$tan\theta_1\tan\theta_2=\frac{b^2}{a^2}-\frac{1}{4}$
$tan(\theta_1+\theta_2)=\frac{\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}-\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}}{1-\frac{b^2}{a^2}+\frac{1}{4}}=-\frac{2b}{ae}$
Therefore, the correct answer is option (C) $tan^{-1}(\frac{b}{ae})$.
Eccentricity of the ellipse: $e=\sqrt{1-\frac{b^2}{a^2}}$
Latus-rectum of the ellipse: $l= \frac{2b^2}{a}$
Extreme points of latus-rectum: $(\pm\frac{l}{2},\pm b)$
Let $\theta_1$ and $\theta_2$ be the eccentric angles of the extreme points of the latus-rectum with respect to the positive x-axis.
We have to find: $tan(\theta_1+\theta_2)$
To find $\theta_1$ and $\theta_2$, we use the formula:
$tan\theta=\frac{b}{a}\sqrt{\frac{a^2-x^2}{x^2}}$
We get:
$tan\theta_1=\frac{b}{a}\sqrt{\frac{a^2-\frac{l^2}{4}}{\frac{l^2}{4}}}=\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}$
$tan\theta_2=\frac{b}{a}\sqrt{\frac{a^2-\frac{l^2}{4}}{\frac{l^2}{4}}}=-\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}$
Using the formula for tan(A+B), we get:
$tan(\theta_1+\theta_2)=\frac{tan\theta_1+tan\theta_2}{1-tan\theta_1\tan\theta_2}$
$tan\theta_1\tan\theta_2=\frac{b^2}{a^2}-\frac{1}{4}$
$tan(\theta_1+\theta_2)=\frac{\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}-\sqrt{\frac{b^2}{a^2}-\frac{1}{4}}}{1-\frac{b^2}{a^2}+\frac{1}{4}}=-\frac{2b}{ae}$
Therefore, the correct answer is option (C) $tan^{-1}(\frac{b}{ae})$.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-Assertion(A):If Cr is the coefficient of xr in the expansion of (1 + x)20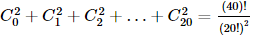 Reason(R) : Cr = Cn − r for any positive integer n
Reason(R) : Cr = Cn − r for any positive integer n- a)Assertion is true but Reason is false.
- b)Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
- c)Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
- d)Assertion is false but Reason is true.
Correct answer is option 'A'. Can you explain this answer?
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A):If Cr is the coefficient of xr in the expansion of (1 + x)20
Reason(R) : Cr = Cn − r for any positive integer n
a)
Assertion is true but Reason is false.
b)
Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
c)
Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
d)
Assertion is false but Reason is true.
|
|
Deepak Yadav answered |
Assertion is correct but the reason is not becoz in reason this concept is not use ..the use concet is that (1+×)²⁰=(×+1)²⁰..so reson is not correct
The conjugate of complex number [(2+5i)/(4-3i)] is- a)[(7-26i)/(25)]
- b)[(-7-26i)/(25)]
- c)[(-7+26i)/(25)]
- d)[(7+26i)/(25)]
Correct answer is option 'B'. Can you explain this answer?
The conjugate of complex number [(2+5i)/(4-3i)] is
a)
[(7-26i)/(25)]
b)
[(-7-26i)/(25)]
c)
[(-7+26i)/(25)]
d)
[(7+26i)/(25)]
|
|
Niharika Gupta answered |
Explanation:
To find the conjugate of a complex number, we change the sign of the imaginary part. In this case, we have the complex number:
\(\frac{2+5i}{4-3i}\)
Step 1: Multiply the numerator and denominator by the conjugate of the denominator.
The conjugate of \(4-3i\) is \(4+3i\), so we multiply both the numerator and denominator by \(4+3i\):
\(\frac{2+5i}{4-3i} \cdot \frac{4+3i}{4+3i}\)
Step 2: Simplify the expression.
Multiplying the numerators and denominators, we get:
\(\frac{(2+5i)(4+3i)}{(4-3i)(4+3i)}\)
Using the FOIL method to expand the numerator and denominator, we have:
\(\frac{8+6i+20i+15i^2}{16+12i-12i-9i^2}\)
Simplifying further, we have:
\(\frac{8+26i+15(-1)}{16+9}\)
\(\frac{-7+26i}{25}\)
Step 3: Identify the conjugate.
The conjugate of \(-7+26i\) is \(-7-26i\).
Therefore, the conjugate of \(\frac{2+5i}{4-3i}\) is \(\frac{-7-26i}{25}\).
Answer: Option B, \(\frac{-7-26i}{25}\), is the correct answer.
To find the conjugate of a complex number, we change the sign of the imaginary part. In this case, we have the complex number:
\(\frac{2+5i}{4-3i}\)
Step 1: Multiply the numerator and denominator by the conjugate of the denominator.
The conjugate of \(4-3i\) is \(4+3i\), so we multiply both the numerator and denominator by \(4+3i\):
\(\frac{2+5i}{4-3i} \cdot \frac{4+3i}{4+3i}\)
Step 2: Simplify the expression.
Multiplying the numerators and denominators, we get:
\(\frac{(2+5i)(4+3i)}{(4-3i)(4+3i)}\)
Using the FOIL method to expand the numerator and denominator, we have:
\(\frac{8+6i+20i+15i^2}{16+12i-12i-9i^2}\)
Simplifying further, we have:
\(\frac{8+26i+15(-1)}{16+9}\)
\(\frac{-7+26i}{25}\)
Step 3: Identify the conjugate.
The conjugate of \(-7+26i\) is \(-7-26i\).
Therefore, the conjugate of \(\frac{2+5i}{4-3i}\) is \(\frac{-7-26i}{25}\).
Answer: Option B, \(\frac{-7-26i}{25}\), is the correct answer.
The probability that a leap year will have exactly 53 Sunday is
- a)1/7
- b)3/7
- c)2/7
- d)5/7
Correct answer is option 'C'. Can you explain this answer?
The probability that a leap year will have exactly 53 Sunday is
a)
1/7
b)
3/7
c)
2/7
d)
5/7
|
|
Naina Bansal answered |
The probability of a year being a leap year is 1/4 and being non-leap is 3/4.A leap year has 366 days or 52 weeks and 2 odd days. The two odd days can be {Sunday,Monday},{Monday,Tuesday},{Tuesday,Wednesday}, Wednesday,Thursday},{Thursday,Friday},{Friday,Saturday},{Saturday,Sunday}.So there are 7 possibiliyies out of which 2 have a Sunday. So the probability of 53 Sundays in a leap year is 2/7.
If arg (z) = θ, then arg(z̅) =- a)θ
- b)-θ
- c)π - θ
- d)θ - π
Correct answer is option 'B'. Can you explain this answer?
If arg (z) = θ, then arg(z̅) =
a)
θ
b)
-θ
c)
π - θ
d)
θ - π
|
|
Tanishq Saini answered |
It seems like you have only provided part of the equation or expression. Could you please provide the complete equation or expression for arg(z)?
If two dice are thrown, find the probability of getting an odd number of on one and multiple of 3 on the other is
- a)1/3
- b)2/3
- c)1/6
- d)13/36
Correct answer is option 'C'. Can you explain this answer?
If two dice are thrown, find the probability of getting an odd number of on one and multiple of 3 on the other is
a)
1/3
b)
2/3
c)
1/6
d)
13/36
|
|
Anjali Sharma answered |
Odd no. on the first die
1, 3, 5
multiple of 3 on the other die
3, 6
now let's see the combination of these two events happening simultaneously
as the question says
(1,3) , (1,6) , (3,3) , (3,6) , (5,6) , (5,3)
total no of favourable events = 6
total no of events throwing two dice simultaneously = 6² = 36
so probability = 6/36 = 1/6
The differential equation which represents the family of plane curves y=exp. (cx) is- a)y'=cy
- b)xy'-logy=0
- c)x log y=yy'
- d)y log y=xy'
Correct answer is option 'A'. Can you explain this answer?
The differential equation which represents the family of plane curves y=exp. (cx) is
a)
y'=cy
b)
xy'-logy=0
c)
x log y=yy'
d)
y log y=xy'

|
Beast answered |
Y=e^cx Differentiating y'=ce^cxy'=c(e^cx) y'=cy
Points (0,0), (2,-1) and (9,2) are vertices of a triangle, then cosB =- a)(11/290)
- b)(√11/290)
- c)(-11/290)
- d)-(√11/290)
Correct answer is option 'C'. Can you explain this answer?
Points (0,0), (2,-1) and (9,2) are vertices of a triangle, then cosB =
a)
(11/290)
b)
(√11/290)
c)
(-11/290)
d)
-(√11/290)
|
|
Ram Mohith answered |
I think the correct answer must be
cos B = -(11/√290)
cos B = -(11/√290)
The sides of a parallelogram are lx + ny + n = 0, lx + my + n' = 0, mx + ly + n = 0, mx + ly + n' = 0, the angle between its diagonals is- a)π/2
- b)π/3
- c)π/4
- d)π
Correct answer is option 'B'. Can you explain this answer?
The sides of a parallelogram are lx + ny + n = 0, lx + my + n' = 0, mx + ly + n = 0, mx + ly + n' = 0, the angle between its diagonals is
a)
π/2
b)
π/3
c)
π/4
d)
π
|
|
Ayushi Singh answered |
I think ques is wrong ...since it's a ||gm ..two pairs of lines must have same slope.
If A, B, C are represented by 3 + 4i, 5 - 2i, -1 + 16i respectively, then A, B, C are- a)collinear
- b)vertices of equilateral triangle
- c)vertices of isosceles triangle
- d)vertices of right angled triangle
Correct answer is option 'A'. Can you explain this answer?
a)
collinear
b)
vertices of equilateral triangle
c)
vertices of isosceles triangle
d)
vertices of right angled triangle
|
|
Jatin Saini answered |
Given, A = 3 + 4i, B = 5 - 2i, C = -1 + 16i.
To check if the points A, B, and C are collinear, we can use the slope formula.
Slope of AB = (y2 - y1) / (x2 - x1) = (-2 - 4) / (5 - 3) = -3
Slope of BC = (y2 - y1) / (x2 - x1) = (16 + 2) / (-1 - 5) = -2
Slope of AC = (y2 - y1) / (x2 - x1) = (16 - 4) / (-1 - 3) = -3
Since the slope of AB and AC are equal, we can conclude that the points A, B, and C are collinear.
Therefore, the correct option is A.
To check if the points A, B, and C are collinear, we can use the slope formula.
Slope of AB = (y2 - y1) / (x2 - x1) = (-2 - 4) / (5 - 3) = -3
Slope of BC = (y2 - y1) / (x2 - x1) = (16 + 2) / (-1 - 5) = -2
Slope of AC = (y2 - y1) / (x2 - x1) = (16 - 4) / (-1 - 3) = -3
Since the slope of AB and AC are equal, we can conclude that the points A, B, and C are collinear.
Therefore, the correct option is A.
In the following question, a Statement-1 is given followed by a corresponding Statement-2 just below it. Read the statements carefully and mark the correct answer-
Consider the planes 3x – 6y – 2z = 15 and 2x + y – 2z = 5.
Statement-1:
The parametric equations of the line of intersection of the given planes are
x = 3 + 14t, y = 1 + 2t, z = 15t.
Statement-2:
The vector 14î+2ĵ+15k̂ is parallel to the line of intersection of given planes- a)Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
- b)Statement-1 is True, Statement-2 is True; Statement-2 is not a correct explanation for Statement-1
- c)Statement-1 is True, Statement-2 is False
- d)Statement-1 is False, Statement-2 is True
Correct answer is option 'D'. Can you explain this answer?
Consider the planes 3x – 6y – 2z = 15 and 2x + y – 2z = 5.
Statement-1:
The parametric equations of the line of intersection of the given planes are
x = 3 + 14t, y = 1 + 2t, z = 15t.
Statement-2:
The vector 14î+2ĵ+15k̂ is parallel to the line of intersection of given planes
a)
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
b)
Statement-1 is True, Statement-2 is True; Statement-2 is not a correct explanation for Statement-1
c)
Statement-1 is True, Statement-2 is False
d)
Statement-1 is False, Statement-2 is True
|
|
Ram Mohith answered |
Statement-1 :Line of intersection of given planes is given by,L = 3x - 6y - 2z - 15 + t(2x + y - 2z - 5) = 0L = (3 + 2t)x + (t - 6)y - 2(1 + t)z - 5(t + 3) = 0So, the parametric equations of the line are: x = 2t + 3, y = t - 6, z = -2(t + 1) Statement-2 :Equation of normal for plane 1 : 3i - 6j - 2kEquation of normal for plane 2 : 2i + j - 2kFor a line to be parallel to the line of intersection of planes then it must be perpendicular to the normal's of the planes. Given line is 14i = 2j = 15k(14i + 2j + 15k)•(3i - 6j - 2k) = 42 - 12 - 30 = 0(14i +2j + 15k)•(2i + j - 2k) = 28 + 2 - 30 = 0Since the dot product's are zero the given line is parallel to the line of intersection of planes.
Which of the following statements are true ?
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes.
(2) For any polynomial f(x) =0 with real co-efficients, imaginary roots occurs in conjugate paris.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers.
(4) The value of ω used as a cube root of unity and as a fourth root of unity are different.- a)(1) and (2) only
- b)(2) and (4) only
- c)(3) and (4) only
- d)(1),(2) and (4) only
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements are true ?
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes.
(2) For any polynomial f(x) =0 with real co-efficients, imaginary roots occurs in conjugate paris.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers.
(4) The value of ω used as a cube root of unity and as a fourth root of unity are different.
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes.
(2) For any polynomial f(x) =0 with real co-efficients, imaginary roots occurs in conjugate paris.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers.
(4) The value of ω used as a cube root of unity and as a fourth root of unity are different.
a)
(1) and (2) only
b)
(2) and (4) only
c)
(3) and (4) only
d)
(1),(2) and (4) only
|
|
Nabanita Nambiar answered |
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes. This statement is true. The amplitude of a complex number is the magnitude or absolute value of the number, and when you take the product of two complex numbers, the absolute values of the numbers multiply together.
(2) For any polynomial f(x) =0 with real coefficients, imaginary roots occur in conjugate pairs. This statement is true. This is known as the conjugate root theorem, which states that if a polynomial with real coefficients has an imaginary root, then its conjugate (with the sign of the imaginary part flipped) is also a root.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers. This statement is false. The real numbers have a natural order relation, where one number can be greater than, less than, or equal to another number. However, complex numbers do not have a natural order relation. It is not meaningful to say that one complex number is greater than or less than another.
(4) The value of e^(πi) is equal to -1. This statement is true. This is known as Euler's identity, which states that e^(πi) + 1 = 0.
(2) For any polynomial f(x) =0 with real coefficients, imaginary roots occur in conjugate pairs. This statement is true. This is known as the conjugate root theorem, which states that if a polynomial with real coefficients has an imaginary root, then its conjugate (with the sign of the imaginary part flipped) is also a root.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers. This statement is false. The real numbers have a natural order relation, where one number can be greater than, less than, or equal to another number. However, complex numbers do not have a natural order relation. It is not meaningful to say that one complex number is greater than or less than another.
(4) The value of e^(πi) is equal to -1. This statement is true. This is known as Euler's identity, which states that e^(πi) + 1 = 0.
A tangent is drawn at the point (3√3 cos θ, sin θ) 0 < θ < (π/2) of an ellipse (x2/27) (y2/1) = 1 the least value of the sum of the intercepts on the co-ordinate axes by this tangent is attained at θ =
- a) π/6
- b) π/3
- c) π/8
- d) π/4
Correct answer is option 'A'. Can you explain this answer?
A tangent is drawn at the point (3√3 cos θ, sin θ) 0 < θ < (π/2) of an ellipse (x2/27) (y2/1) = 1 the least value of the sum of the intercepts on the co-ordinate axes by this tangent is attained at θ =
a)
π/6b)
π/3c)
π/8d)
π/4|
|
User2408930 answered |

If 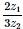 is a purely imaginary number, then
is a purely imaginary number, then 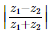 is equal to
is equal to- a)3/2
- b)1
- c)2/3
- d)4/9
Correct answer is option 'B'. Can you explain this answer?
If 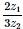 is a purely imaginary number, then
is a purely imaginary number, then 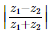 is equal to
is equal to
a)
3/2
b)
1
c)
2/3
d)
4/9
|
|
Aabhi Gulia answered |
The phenomenon of beats can take place
a) for longitudinal waves only
b) for transverse waves only
c) for both
d) for sound wave only
explain your answer briefly
a) for longitudinal waves only
b) for transverse waves only
c) for both
d) for sound wave only
explain your answer briefly
If the coefficient of correlation between x and y is 0.28, covariance between x and y is 7.6, and the variance of x is 9, then the standard deviation of the y series is- a)9.8
- b)10.1
- c)9.05
- d)10.05
Correct answer is option 'C'. Can you explain this answer?
a)
9.8
b)
10.1
c)
9.05
d)
10.05
|
|
Naina Bansal answered |
N the given problem it is SD of x is 3: (or Variance of x is 9). As Variance = (Sx)^2. We know the relation : correlation coefficient (r) = Cov (x,y) / (Sx * Sy) so, 0.28 = 7.6 / (3 * Sy) From here we get the value of SD of Y : Sy = 9.05.
If a, b and c are perpendicular to b + c, c + a and a + b respectively and if |a + b| = 6, |b + c| = 8 and |c + a| = 10 then |a + b + c| =
Correct answer is '10'. Can you explain this answer?
If a, b and c are perpendicular to b + c, c + a and a + b respectively and if |a + b| = 6, |b + c| = 8 and |c + a| = 10 then |a + b + c| =
|
|
Janani Menon answered |
Understanding the Problem
In this problem, we have three vectors a, b, and c that are orthogonal to the resultant vectors formed by adding the other two vectors. Specifically:
- a is perpendicular to b + c
- b is perpendicular to c + a
- c is perpendicular to a + b
We are given the magnitudes of the sums of these vectors:
- |a + b| = 6
- |b + c| = 8
- |c + a| = 10
Using the Perpendicular Condition
Since a is perpendicular to b + c, we can express this condition mathematically:
- a • (b + c) = 0
Similarly, we can write the conditions for b and c:
- b • (c + a) = 0
- c • (a + b) = 0
Finding the Magnitude of a + b + c
To find |a + b + c|, we can use the identity:
|a + b + c|^2 = |a|^2 + |b|^2 + |c|^2 + 2(a • b + b • c + c • a)
From the given magnitudes, we have:
- |a + b|^2 = 36
- |b + c|^2 = 64
- |c + a|^2 = 100
Now, applying the square of the magnitudes:
|a + b|^2 = |a|^2 + |b|^2 + 2(a • b) = 36
|b + c|^2 = |b|^2 + |c|^2 + 2(b • c) = 64
|c + a|^2 = |c|^2 + |a|^2 + 2(c • a) = 100
Solving the Equations
Adding these three equations and simplifying gives us:
2(|a|^2 + |b|^2 + |c|^2) + 2(a • b + b • c + c • a) = 200
Now, substituting values and simplifying leads us to find:
|a + b + c| = 10.
Conclusion
Thus, the magnitude |a + b + c| is correctly found to be 10, confirming the result through the conditions of orthogonality and the properties of vector magnitudes.
In this problem, we have three vectors a, b, and c that are orthogonal to the resultant vectors formed by adding the other two vectors. Specifically:
- a is perpendicular to b + c
- b is perpendicular to c + a
- c is perpendicular to a + b
We are given the magnitudes of the sums of these vectors:
- |a + b| = 6
- |b + c| = 8
- |c + a| = 10
Using the Perpendicular Condition
Since a is perpendicular to b + c, we can express this condition mathematically:
- a • (b + c) = 0
Similarly, we can write the conditions for b and c:
- b • (c + a) = 0
- c • (a + b) = 0
Finding the Magnitude of a + b + c
To find |a + b + c|, we can use the identity:
|a + b + c|^2 = |a|^2 + |b|^2 + |c|^2 + 2(a • b + b • c + c • a)
From the given magnitudes, we have:
- |a + b|^2 = 36
- |b + c|^2 = 64
- |c + a|^2 = 100
Now, applying the square of the magnitudes:
|a + b|^2 = |a|^2 + |b|^2 + 2(a • b) = 36
|b + c|^2 = |b|^2 + |c|^2 + 2(b • c) = 64
|c + a|^2 = |c|^2 + |a|^2 + 2(c • a) = 100
Solving the Equations
Adding these three equations and simplifying gives us:
2(|a|^2 + |b|^2 + |c|^2) + 2(a • b + b • c + c • a) = 200
Now, substituting values and simplifying leads us to find:
|a + b + c| = 10.
Conclusion
Thus, the magnitude |a + b + c| is correctly found to be 10, confirming the result through the conditions of orthogonality and the properties of vector magnitudes.
How many numbers between 99 and 1000 can be formed from the digits 2,3,7,0,8,6 so that in each number each digit may occur once only?- a)100
- b)90
- c)120
- d)80
Correct answer is option 'A'. Can you explain this answer?
How many numbers between 99 and 1000 can be formed from the digits 2,3,7,0,8,6 so that in each number each digit may occur once only?
a)
100
b)
90
c)
120
d)
80
|
|
Charvi Khanna answered |
Solution:
To find the total number of numbers that can be formed from the given digits, we must first calculate the total number of permutations of the given digits.
Total number of permutations of the given digits = 6P6 = 720
Now, we need to find the number of such permutations that lie between 99 and 1000.
Numbers between 99 and 1000 can be of the form:
1. _ _ _
2. 1 _ _
3. 9 _ _
Case 1:
For the first digit, we have 4 choices (2, 3, 7, 8) as 0 cannot be the first digit.
For the second digit, we have 5 choices (0, 2, 3, 7, 8) as any of the remaining 5 digits can be used.
For the third digit, we have 4 choices (remaining 4 digits) as we cannot repeat any digit.
Total number of permutations in case 1 = 4 × 5 × 4 = 80
Case 2:
For the second and third digits, we have 5 and 4 choices respectively (as explained above).
Total number of permutations in case 2 = 1 × 5 × 4 = 20
Case 3:
For the third digit, we have 3 choices (0, 2, 3) as we cannot use 7, 8, or 6.
Total number of permutations in case 3 = 1 × 1 × 3 = 3
Total number of required permutations = 80 + 20 + 3 = 103
Therefore, the correct option is (A) 100.
To find the total number of numbers that can be formed from the given digits, we must first calculate the total number of permutations of the given digits.
Total number of permutations of the given digits = 6P6 = 720
Now, we need to find the number of such permutations that lie between 99 and 1000.
Numbers between 99 and 1000 can be of the form:
1. _ _ _
2. 1 _ _
3. 9 _ _
Case 1:
For the first digit, we have 4 choices (2, 3, 7, 8) as 0 cannot be the first digit.
For the second digit, we have 5 choices (0, 2, 3, 7, 8) as any of the remaining 5 digits can be used.
For the third digit, we have 4 choices (remaining 4 digits) as we cannot repeat any digit.
Total number of permutations in case 1 = 4 × 5 × 4 = 80
Case 2:
For the second and third digits, we have 5 and 4 choices respectively (as explained above).
Total number of permutations in case 2 = 1 × 5 × 4 = 20
Case 3:
For the third digit, we have 3 choices (0, 2, 3) as we cannot use 7, 8, or 6.
Total number of permutations in case 3 = 1 × 1 × 3 = 3
Total number of required permutations = 80 + 20 + 3 = 103
Therefore, the correct option is (A) 100.
If i2 = -1, then the sum i + i2 + i3 + ..... upto 1000 terms is equal to- a)1
- b)-1
- c)i
- d)0
Correct answer is option 'D'. Can you explain this answer?
If i2 = -1, then the sum i + i2 + i3 + ..... upto 1000 terms is equal to
a)
1
b)
-1
c)
i
d)
0

|
Anshika Singh answered |
There will equal n opposite signed terms that is 500 +ve one and 500-ve one therefore it's value comes to zero.
The total expenditure incurred by an industry under different heads is best presented as a- a)bar diagram
- b)pie diagram
- c)histogram
- d)frequency polygon
Correct answer is option 'B'. Can you explain this answer?
The total expenditure incurred by an industry under different heads is best presented as a
a)
bar diagram
b)
pie diagram
c)
histogram
d)
frequency polygon
|
|
Neha Joshi answered |
A pie chart is a circular statistical graphic, which is divided into slices to illustrate numerical proportion. In a pie chart, the arc length of each slice, is proportional to the quantity it represents.
The length of the tangent from (0,0) to the circle 2x2 + 2y2 + 7x -7 y + 5 = 0 is
- a)√5
- b)√5 ∕ 2
- c)√2
- d)
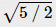
Correct answer is option 'D'. Can you explain this answer?
The length of the tangent from (0,0) to the circle 2x2 + 2y2 + 7x -7 y + 5 = 0 is
a)
√5
b)
√5 ∕ 2
c)
√2
d)

|
Learners Habitat answered |
We have
S=2(x2+y2)+7x−7y+5=0
=x2+y2+7/2x−7/2y+5/2=0
Length of tangent from (0,0) =√S1
=√5/2
Hence, the required answer is √5/2.
Log (x + y) - 2xy = 0, then y (0) =- a)1
- b)-1
- c)2
- d)0
Correct answer is option 'A'. Can you explain this answer?
a)
1
b)
-1
c)
2
d)
0
|
|
Kritika Yadav answered |
Understanding the Equation
The equation given is:
Log(x + y) - 2xy = 0
This can be rewritten as:
Log(x + y) = 2xy
We need to analyze this equation for y(0) when x = 0.
Substituting x = 0
When we substitute x = 0 into the equation, we have:
Log(0 + y) = 2(0)y
Log(y) = 0
Solving for y
The equation Log(y) = 0 implies:
y = e^0
y = 1
Thus, when x = 0, y(0) = 1.
Verifying the Result
Let’s verify:
- If y = 1, substituting back into the original equation gives:
Log(0 + 1) - 2(0)(1) = Log(1) - 0 = 0
The equation holds true, confirming our solution.
Conclusion
The value of y(0) is indeed:
a) 1
This aligns with the correct answer provided. Therefore, option 'A' is validated as the answer to the problem.
The equation given is:
Log(x + y) - 2xy = 0
This can be rewritten as:
Log(x + y) = 2xy
We need to analyze this equation for y(0) when x = 0.
Substituting x = 0
When we substitute x = 0 into the equation, we have:
Log(0 + y) = 2(0)y
Log(y) = 0
Solving for y
The equation Log(y) = 0 implies:
y = e^0
y = 1
Thus, when x = 0, y(0) = 1.
Verifying the Result
Let’s verify:
- If y = 1, substituting back into the original equation gives:
Log(0 + 1) - 2(0)(1) = Log(1) - 0 = 0
The equation holds true, confirming our solution.
Conclusion
The value of y(0) is indeed:
a) 1
This aligns with the correct answer provided. Therefore, option 'A' is validated as the answer to the problem.
sin⁻1 (cos(sin⁻1 x) + cos⁻1 (sin(cos⁻1 x) is equal to- a)0
- b)π/4
- c)π/2
- d)3π/4
Correct answer is option 'C'. Can you explain this answer?
sin⁻1 (cos(sin⁻1 x) + cos⁻1 (sin(cos⁻1 x) is equal to
a)
0
b)
π/4
c)
π/2
d)
3π/4
|
|
Sneha Singh answered |
Both interior angle belogs to [0,π/2]
that's why sum is π/2
that's why sum is π/2
The orthocentre of a triangle whose vertices are [(2),((√3-1)/2)], ((1/2),-(1/2)) and (2,-(1/2)) is- a)[(3/2),((√3-2)/2)]
- b)[(2),(-1/2)]
- c)[(5/4),((√3-2)/4)]
- d)[(1/2),-(1/2)]
Correct answer is option 'B'. Can you explain this answer?
a)
[(3/2),((√3-2)/2)]
b)
[(2),(-1/2)]
c)
[(5/4),((√3-2)/4)]
d)
[(1/2),-(1/2)]
|
|
Bijoy Chawla answered |
To find the orthocentre of a triangle, we need to find the intersection point of the altitudes of the triangle.
Let's label the given vertices of the triangle as A, B, and C:
A = (2, (√3-1)/2)
B = (1/2, -1/2)
C = (2, -1/2)
**Step 1: Find the slopes of the sides**
To find the slopes of the sides of the triangle, we can use the formula:
slope = (y2 - y1) / (x2 - x1)
Slope of AB:
mAB = ((√3-1)/2 - (-1/2)) / (2 - 1/2)
= (√3 - 1 + 1/2) / (3/2)
= (√3 - 1 + 1/2) * (2/3)
= (√3 - 1 + 1/2) * (2/3)
Slope of BC:
mBC = ((-1/2) - (-1/2)) / (1/2 - 2)
= 0 / (-3/2)
= 0
Slope of AC:
mAC = ((√3-1)/2 - (-1/2)) / (2 - 2)
= ((√3-1)/2 + 1/2) / 0
= (√3-1)/2 / 0
= undefined
**Step 2: Find the equations of the altitudes**
To find the equations of the altitudes, we need to find the slopes of the altitudes. The slopes of the altitudes are negative reciprocals of the slopes of the sides.
Slope of altitude AD (perpendicular to BC) = -1/mBC = undefined
Since the slope is undefined, AD is a vertical line passing through the point A.
Slope of altitude BE (perpendicular to AC) = -1/mAC = 0
Since the slope is 0, BE is a horizontal line passing through the point B.
Slope of altitude CF (perpendicular to AB) = -1/mAB = -3/(√3 - 1 + 1/2) * (2/3)
**Step 3: Find the equations of the altitudes**
Using the point-slope form of a line, we can find the equations of the altitudes.
Equation of AD:
x = 2
Equation of BE:
y = -1/2
Equation of CF:
y - (-1/2) = -3/(√3 - 1 + 1/2) * (2/3)(x - 1/2)
Simplifying the equation gives:
y = (-3√3 + 3/2)x + (3√3 - 5/4)
**Step 4: Find the intersection point of the altitudes (orthocentre)**
To find the orthocentre, we need to find the point of intersection of the three altitudes.
From the equations of the altitudes, we have:
AD: x = 2
BE: y = -1/2
CF: y = (-3√3 + 3/2)x +
Let's label the given vertices of the triangle as A, B, and C:
A = (2, (√3-1)/2)
B = (1/2, -1/2)
C = (2, -1/2)
**Step 1: Find the slopes of the sides**
To find the slopes of the sides of the triangle, we can use the formula:
slope = (y2 - y1) / (x2 - x1)
Slope of AB:
mAB = ((√3-1)/2 - (-1/2)) / (2 - 1/2)
= (√3 - 1 + 1/2) / (3/2)
= (√3 - 1 + 1/2) * (2/3)
= (√3 - 1 + 1/2) * (2/3)
Slope of BC:
mBC = ((-1/2) - (-1/2)) / (1/2 - 2)
= 0 / (-3/2)
= 0
Slope of AC:
mAC = ((√3-1)/2 - (-1/2)) / (2 - 2)
= ((√3-1)/2 + 1/2) / 0
= (√3-1)/2 / 0
= undefined
**Step 2: Find the equations of the altitudes**
To find the equations of the altitudes, we need to find the slopes of the altitudes. The slopes of the altitudes are negative reciprocals of the slopes of the sides.
Slope of altitude AD (perpendicular to BC) = -1/mBC = undefined
Since the slope is undefined, AD is a vertical line passing through the point A.
Slope of altitude BE (perpendicular to AC) = -1/mAC = 0
Since the slope is 0, BE is a horizontal line passing through the point B.
Slope of altitude CF (perpendicular to AB) = -1/mAB = -3/(√3 - 1 + 1/2) * (2/3)
**Step 3: Find the equations of the altitudes**
Using the point-slope form of a line, we can find the equations of the altitudes.
Equation of AD:
x = 2
Equation of BE:
y = -1/2
Equation of CF:
y - (-1/2) = -3/(√3 - 1 + 1/2) * (2/3)(x - 1/2)
Simplifying the equation gives:
y = (-3√3 + 3/2)x + (3√3 - 5/4)
**Step 4: Find the intersection point of the altitudes (orthocentre)**
To find the orthocentre, we need to find the point of intersection of the three altitudes.
From the equations of the altitudes, we have:
AD: x = 2
BE: y = -1/2
CF: y = (-3√3 + 3/2)x +
The number of tangents drawn from the point (-1,2) to x2+y2+2x-4y+4=0 is
- a)1
- b)2
- c)3
- d)0
Correct answer is option 'D'. Can you explain this answer?
The number of tangents drawn from the point (-1,2) to x2+y2+2x-4y+4=0 is
a)
1
b)
2
c)
3
d)
0

|
Wrik Karmakar answered |
The centre of the circle is (-1,2), so no tangents pass through it.
Determinant 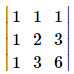 equals to
equals to- a)

- b)

- c)

- d)
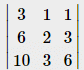
Correct answer is option 'A'. Can you explain this answer?
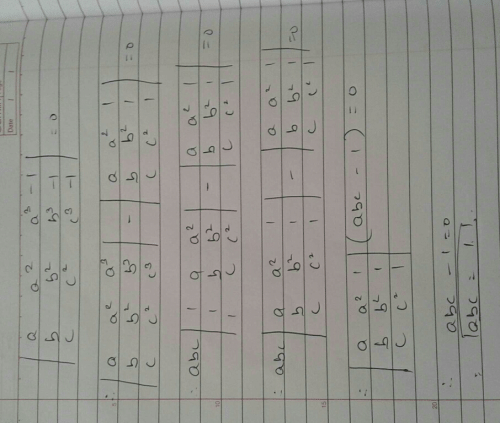
Determinant 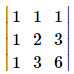 equals to
equals to
a)
b)
c)
d)

|
Anand Kumar answered |
Determinants of the given questions is equal to 1.So ,let's check the option.(I) Taking common 2 from C1. Value = 2. Hence , (a) is not correct answer.(2) find the determinant you will get it will be equal to 1.Hence, correct answer is (B).
If the equation [(k(x+1)2/3)]+[(y+2)2/4]=1 represents a circle, then k=- a)3/4
- b)1
- c)4/3
- d)6
Correct answer is option 'A'. Can you explain this answer?
If the equation [(k(x+1)2/3)]+[(y+2)2/4]=1 represents a circle, then k=
a)
3/4
b)
1
c)
4/3
d)
6
|
|
Rounak Shah answered |
Solution:
Concept: The standard equation of a circle with center (h, k) and radius r is given by (x - h)² + (y - k)² = r².
We can convert the given equation to the standard equation of a circle by using the following steps:
Step 1: Rewrite the equation as (k(x^(1/3))^2) * (y^(1/2))^2 = 1.
Step 2: Take the square root of both sides to get k(x^(1/3)) * y^(1/2) = ±1.
Step 3: Square both sides to get k^2 * x^(2/3) * y = 1.
Step 4: Compare this equation to the standard equation of a circle to get:
x - h = k^2 * x^(2/3)
y - k = k^2 * y^(2/3)
where h = 0, k = 0, and r = (1/k^2)^(1/2/3) = k^(-2/3).
Step 5: Solve for k by substituting x = 1 and y = 0 into the equation for the circle:
(1 - 0)^2 + (0 - 0)^2 = r^2
1 = r^2
1 = k^(-4/3)
k = 1^(3/4) = 3/4
Therefore, the answer is (A) 3/4.
Concept: The standard equation of a circle with center (h, k) and radius r is given by (x - h)² + (y - k)² = r².
We can convert the given equation to the standard equation of a circle by using the following steps:
Step 1: Rewrite the equation as (k(x^(1/3))^2) * (y^(1/2))^2 = 1.
Step 2: Take the square root of both sides to get k(x^(1/3)) * y^(1/2) = ±1.
Step 3: Square both sides to get k^2 * x^(2/3) * y = 1.
Step 4: Compare this equation to the standard equation of a circle to get:
x - h = k^2 * x^(2/3)
y - k = k^2 * y^(2/3)
where h = 0, k = 0, and r = (1/k^2)^(1/2/3) = k^(-2/3).
Step 5: Solve for k by substituting x = 1 and y = 0 into the equation for the circle:
(1 - 0)^2 + (0 - 0)^2 = r^2
1 = r^2
1 = k^(-4/3)
k = 1^(3/4) = 3/4
Therefore, the answer is (A) 3/4.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
A committee of n persons is to be formed out of 30 persons.
Assertion(A) : The value of n for which the number of committees is maximum is n = 15
Reason(R) : In the expansion of (1 + x)k , k ∈ N , the middle term has the greatest binomial coefficient.- a)Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
- c)Assertion is true but Reason is false.
- d)Assertion is false but Reason is true.
Correct answer is option 'A'. Can you explain this answer?
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
A committee of n persons is to be formed out of 30 persons.
Assertion(A) : The value of n for which the number of committees is maximum is n = 15
Reason(R) : In the expansion of (1 + x)k , k ∈ N , the middle term has the greatest binomial coefficient.
A committee of n persons is to be formed out of 30 persons.
Assertion(A) : The value of n for which the number of committees is maximum is n = 15
Reason(R) : In the expansion of (1 + x)k , k ∈ N , the middle term has the greatest binomial coefficient.
a)
Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
c)
Assertion is true but Reason is false.
d)
Assertion is false but Reason is true.
|
|
Arjun answered |
Please elaborate it
Chapter doubts & questions for JEE Maths Mocks - JEE Main & Advanced Mock Test Series 2025 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of JEE Maths Mocks - JEE Main & Advanced Mock Test Series 2025 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup














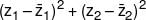 is equal to -
is equal to -