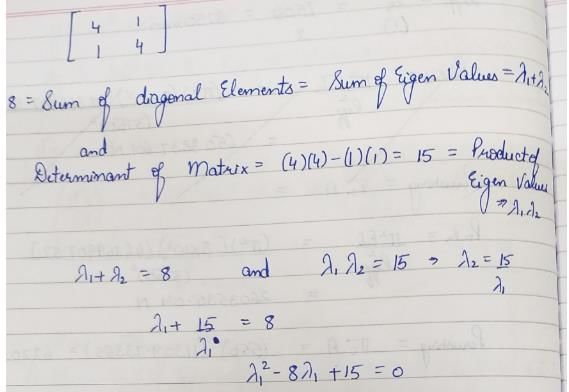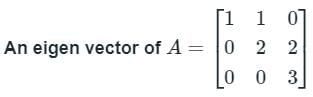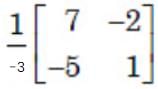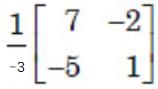All questions of Engineering Mathematics for Electrical Engineering (EE) Exam
If A is a non–singular matrix and the eigen values of A are 2 , 3 , -3 then the eigen values of A-1 are- a)2 , 3 , - 3
- b)1/2, 1/3, -1/3
- c)2|A|, 3|A|, -3|A|
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If A is a non–singular matrix and the eigen values of A are 2 , 3 , -3 then the eigen values of A-1 are
a)
2 , 3 , - 3
b)
1/2, 1/3, -1/3
c)
2|A|, 3|A|, -3|A|
d)
None of these
|
Tanishq Chavan answered |
If λ1 ,λ2 ,λ3 ....λn are the eigen values of a non–singular matrix A, then A-1 has the eigen values 1/λ1 ,1/λ2 ,1/λ3 ....1/λn Thus eigen values of A-1are 1/2, 1/3, -1/3
Given the matrix 
the eigenvector is- a)
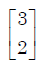
- b)
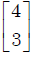
- c)
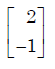
- d)
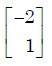
Correct answer is 'C'. Can you explain this answer?
Given the matrix 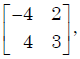the eigenvector is
the eigenvector isa)
b)
c)
d)
|
Ritika Bose answered |
Characteristic equation
The number of linearly independent eigenvectors of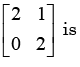 
- a)0
- b)1
- c)2
- d)Infinit e
Correct answer is 'B'. Can you explain this answer?
The number of linearly independent eigenvectors of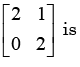
a)
0
b)
1
c)
2
d)
Infinit e
|
Pranjal Sen answered |
Number of linear independent vectors is equal to the sum of Geometric Multiplicity of eigen values. Here only eigen value is 2. To find Geometric multiplicity find n-r of (matrix-2I), where n is order and r is rank. Rank of obtained matrix is 1 and n=2 so n-r=1. Therefore the no of linearly independent eigen vectors is 1
The eigenvalues of
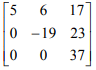
- a)-19,5,37
- b)19,-5,-37
- c)2,-3,7
- d)3,-5,37
Correct answer is option 'A'. Can you explain this answer?
The eigenvalues of
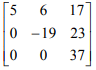
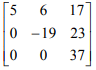
a)
-19,5,37
b)
19,-5,-37
c)
2,-3,7
d)
3,-5,37
|
|
Avinash Sharma answered |
The eigenvalues of an upper triangular matrix are simply the diagonal entries of the matrix.
Hence 5, -19, and 37 are the eigenvalues of the matrix. Alternately, look atd
λ = 5, -19, 37
For a skew symmetric even ordered matrix A of integers, which of the following will not hold true:- a)det(A) = 7
- b)det(A) = 81
- c)det(A) = 9
- d)det(A) = 4
Correct answer is option 'A'. Can you explain this answer?
For a skew symmetric even ordered matrix A of integers, which of the following will not hold true:
a)
det(A) = 7
b)
det(A) = 81
c)
det(A) = 9
d)
det(A) = 4
|
Mrinalini Chavan answered |
A skew symmetric matrix Anxn is a matrix with AT = -A. The matrix of (A) satisfy this condition.
If -1 , 2 , 3 are the eigen values of a square matrix A then the eigen values of A2 are- a)-1 , 2 , 3
- b)1, 4, 9
- c)1, 2, 3
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If -1 , 2 , 3 are the eigen values of a square matrix A then the eigen values of A2 are
a)
-1 , 2 , 3
b)
1, 4, 9
c)
1, 2, 3
d)
None of these
|
Aditya Patel answered |
If λ1 ,λ2 ,λ3 ....λn are the eigen values of a matrix A, then A2 has the eigen values λ12 ,λ22 ,λ32 ....λn2 So, eigen values of A2 are 1, 4, 9.
The CORRECT formula for the sentence, "not all rainy days are cold” is- a)
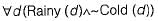
- b)
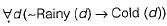
- c)
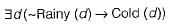
- d)
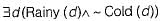
Correct answer is option 'B'. Can you explain this answer?
The CORRECT formula for the sentence, "not all rainy days are cold” is
a)
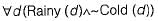
b)
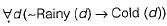
c)
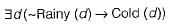
d)
|
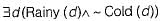
Sanvi Kapoor answered |
In other words it says ``Some rainy days are not cold"
Given statement is
¬∀d[R(d)→C(d)]
¬∀d[R(d)→C(d)]
≡¬∀d[¬R(d)∨C(d)
≡∃d[R(d)∧¬C(d)]
≡∃d[R(d)∧¬C(d)]
Eigen values of a matrix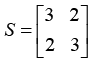 
are 5 and 1. What are the eigen values of the matrix S2 = SS?- a)1 and 25
- b)6 and 4
- c)5 and 1
- d)2 and 10
Correct answer is option 'A'. Can you explain this answer?
Eigen values of a matrix 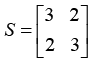are 5 and 1. What are the eigen values of the matrix S2 = SS?
are 5 and 1. What are the eigen values of the matrix S2 = SS?a)
1 and 25
b)
6 and 4
c)
5 and 1
d)
2 and 10
|
EduRev GATE answered |
We know If λ be the eigen value of A ⇒λ2 is an eigen value of A2 .
For S matrix, if eigen values are λ1, λ2, λ3,... then for S² matrix, the eigen values will be λ²1 λ²2 λ²3......
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25
If 1 and 3 are the eigenvalues of a square matrix A then A3 is equal to- a)13 (A - I2 )
- b)13A - 12 I2
- c)12 (A - I2)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 1 and 3 are the eigenvalues of a square matrix A then A3 is equal to
a)
13 (A - I2 )
b)
13A - 12 I2
c)
12 (A - I2)
d)
None of these
|
Pankaj Rane answered |
Since 1 and 3 are the eigenvalues of A so the characteristic equation of A is
Also, by Cayley–Hamilton theorem, every square matrix satisfies its own characteristic equation so
The three characteristic roots of the following matrix A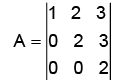 
- a)2,3
- b)1,2,2
- c)1,0,0
- d)0,2,3
Correct answer is option 'B'. Can you explain this answer?
The three characteristic roots of the following matrix A
a)
2,3
b)
1,2,2
c)
1,0,0
d)
0,2,3
|
Kabir Verma answered |
A is lower triangular matrix. So eigen values are only the diagonal elements.
the eigen value are
If 2 and 4 are the eigen values of A then the eigenvalues of AT are
- a)1/2, 1/4
- b)2, 4
- c)4, 16
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 2 and 4 are the eigen values of A then the eigenvalues of AT are
a)
1/2, 1/4
b)
2, 4
c)
4, 16
d)
None of these
|
|
Sanvi Kapoor answered |
The eigenvalues of a matrix A are the roots of the characteristic equation of A, which are invariant under the transpose operation. This means that the matrix A and its transpose AT have the same eigenvalues.
Given that 2 and 4 are the eigenvalues of A, the eigenvalues of AT will also be 2 and 4.
are –2 and 6, respectively. What is the other eigen value? 
Minimum of the real valued function f(x) = (x-1)2/3 occurs at x equal to- a)- ∝
- b)0
- c)1
- d)∝
Correct answer is option 'C'. Can you explain this answer?
Minimum of the real valued function f(x) = (x-1)2/3 occurs at x equal to
a)
- ∝
b)
0
c)
1
d)
∝
|
Kunal Gupta answered |
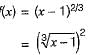
As f(x) is square of hence its minimum value be 0 where at x = 1.
The state variable description of a linear autonomous system is, X= AX, Where X is the two dimensional state vector and A is the system matrix given by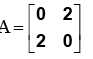 
The roots of the characteristic equation are - a)-2 and +2
- b)-j2 and +j2
- c)-2 and -2
- d)+2 and +2
Correct answer is option 'A'. Can you explain this answer?
The state variable description of a linear autonomous system is, X= AX,
Where X is the two dimensional state vector and A is the system matrix given by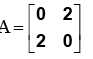
The roots of the characteristic equation are
a)
-2 and +2
b)
-j2 and +j2
c)
-2 and -2
d)
+2 and +2
|
Janhavi Sarkar answered |
Characteristic equation will be :λ2 -4 =0 thus root of characteristic equation will be +2 and - 2.
In an M × N matrix such that all non-zero entries are covered in a rows and b column. Then the maximum number of non-zero entries, such that no two are on the same row or column, is - a)≤ a + b
- b)≤ max (a, b)
- c)≤ min[ M –a, N–b]
- d)≤ min {a, b}
Correct answer is option 'D'. Can you explain this answer?
In an M × N matrix such that all non-zero entries are covered in a rows and b column. Then the maximum number of non-zero entries, such that no two are on the same row or column, is
a)
≤ a + b
b)
≤ max (a, b)
c)
≤ min[ M –a, N–b]
d)
≤ min {a, b}
|
Naroj Boda answered |
Suppose a < b, for example let a = 3, b= 5, then we can put non-zero entries only in 3 rows and 5 columns. So suppose we put non-zero entries in any 3 rows in 3 different columns. Now we can’t put any other non-zero entry anywhere in matrix, because if we put it in some other row, then we will have 4 rows containing non-zeros, if we put it in one of those 3 rows, then we will have more than one non-zero entry in one row, which is not allowed.
So we can fill only “a” non-zero entries if a < b, similarly if b < a, we can put only “b” non-zero entries. So answer is ≤min(a,b), because whatever is less between a and b, we can put atmost that many non-zero entries.
If the rank of a (5×6) matrix Q is 4, then which one of the following statements is correct? - a)Q will have four linearly independent rows and four linearly independent columns
- b)Q will have four lineally independent rows and five lineally independent columns
- c)QQT will be invertible
- d)QTQ will be invertible
Correct answer is option 'A'. Can you explain this answer?
If the rank of a (5×6) matrix Q is 4, then which one of the following statements is correct?
a)
Q will have four linearly independent rows and four linearly independent columns
b)
Q will have four lineally independent rows and five lineally independent columns
c)
QQT will be invertible
d)
QTQ will be invertible
|
Kaavya Sengupta answered |
Given that rank Q is 4, so it will have 4 linearly independent columns as well as 4 linearly independent rows (∵ row rank of a matrix = column rank of a matrix)
So, A is correct and accordingly B is false.
C is false as order of QQ^T will be 5 x 5 and given that rank of Q is 4 i.e. < 5. So the matrix is QQ^T will be singular and hence not invertible.
Similarly D is false as order of Q^T Q will be 6 x 6 and the matrix is Q^T Q will be singular and hence not invertible.
The eigen values of the following matrix are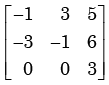 
- a)3, 3 + 5j, –6 – j
- b)–6 + 5j, 3 + j, 3 – j
- c)3+ j, 3 – j, 5 + j
- d)3, –1 + 3j, –1 – 3j
Correct answer is option 'D'. Can you explain this answer?
The eigen values of the following matrix are
a)
3, 3 + 5j, –6 – j
b)
–6 + 5j, 3 + j, 3 – j
c)
3+ j, 3 – j, 5 + j
d)
3, –1 + 3j, –1 – 3j
|
|
Janhavi Singh answered |
Let the matrix be A. We know, Trace (A)=sum of eigen values.
Cayley - Hamiltion Theorem states that square matrix satisfies its own characteristic equation, Consider a matrix
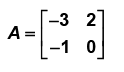A satisfies the relation
- a)A +3I + 2A -2 =0
- b)A2+2A +2I=0
- c)(A+1I)( A+2I)=0
- d)exp(A) =0
Correct answer is option 'C'. Can you explain this answer?
Cayley - Hamiltion Theorem states that square matrix satisfies its own characteristic equation, Consider a matrix
A satisfies the relation
a)
A +3I + 2A -2 =0
b)
A2+2A +2I=0
c)
(A+1I)( A+2I)=0
d)
exp(A) =0
|
Telecom Tuners answered |
Characteristic equation of A is
are nonzero, and one of its eigen values is zero. Which of the following statements is true?
For which value of x will the matrix given below become singular?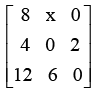 
- a)4
- b)6
- c)8
- d)12
Correct answer is option 'A'. Can you explain this answer?
For which value of x will the matrix given below become singular?
a)
4
b)
6
c)
8
d)
12
|
Gate Funda answered |
Let the given matrix be A. A is singular.
The sum of the eigenvalues of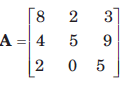 
is equal to - a)18
- b)15
- c)10
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The sum of the eigenvalues of 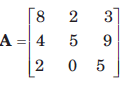is equal to
is equal to a)
18
b)
15
c)
10
d)
none of these
|
Zoya Sharma answered |
- Since the sum of the eigenvalues of an n–square matrix is equal to the trace of the matrix (i.e. sum of the diagonal elements)
- So, required sum = 8 + 5 + 5 = 18
Solution for the system defined by the set of equations
4y + 3z = 8;
2x – z = 2
and 3x + 2y =5 is - a)x = 0; y = 1; z = 4/3
- b)x = 0; y = 1/2 ; z = 2
- c)x = 1; y = 1/2 ; z = 2
- d)non-existent
Correct answer is option 'D'. Can you explain this answer?
Solution for the system defined by the set of equations
4y + 3z = 8;
2x – z = 2
and 3x + 2y =5 is
4y + 3z = 8;
2x – z = 2
and 3x + 2y =5 is
a)
x = 0; y = 1; z = 4/3
b)
x = 0; y = 1/2 ; z = 2
c)
x = 1; y = 1/2 ; z = 2
d)
non-existent
|
Dishani Desai answered |
Ans.(d)
Consider the matrix A =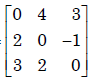
,Now det (A) = 0
So byCramer's Rule the system has no solution
Consider the matrix A =
,Now det (A) = 0So byCramer's Rule the system has no solution
Two dice are thrown simultaneously. The probability that at least one of them will have 6 facing up is - a)1/36
- b)1/3
- c)25/36
- d)11/36
Correct answer is option 'D'. Can you explain this answer?
Two dice are thrown simultaneously. The probability that at least one of them will have 6 facing up is
a)
1/36
b)
1/3
c)
25/36
d)
11/36
|
|
Ravi Singh answered |
P(atleast one of dice will have 6 facing
= 1 - P(none of dice have 6 facing up)
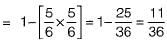
= 1 - P(none of dice have 6 facing up)
The following system of equations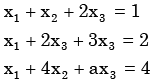 
has a unique solution. The only possible value(s) for a is/are - a)0
- b)either 0 or 1
- c)one of 0, 1 or –1
- d)any real number other than 5
Correct answer is option 'D'. Can you explain this answer?
The following system of equations
has a unique solution. The only possible value(s) for a is/are
a)
0
b)
either 0 or 1
c)
one of 0, 1 or –1
d)
any real number other than 5
|
|
Gate Funda answered |
System has unique Soln if rank (A) = rank ( A ) = 3 . It is possible if a ≠ 5.
the eigen value corresponding to the eigenvector 
The number of linearly independent eigenvectors of 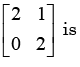- a)0
- b)1
- c)2
- d)Infinit e
Correct answer is option 'B'. Can you explain this answer?
The number of linearly independent eigenvectors of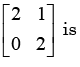
a)
0
b)
1
c)
2
d)
Infinit e
|
|
Ravi Singh answered |
Number of linear independent vectors is equal to the sum of Geometric Multiplicity of eigen values. Here only eigen value is 2. To find Geometric multiplicity find n-r of (matrix-2I), where n is order and r is rank. Rank of obtained matrix is 1 and n=2 so n-r=1. Therefore the no of linearly independent eigen vectors is 1
If the arithmetic mean of two numbers is 10 and their geometric mean is 8, the numbers are- a)12, 18
- b)16, 4
- c)15, 5
- d)20, 5
Correct answer is option 'B'. Can you explain this answer?
If the arithmetic mean of two numbers is 10 and their geometric mean is 8, the numbers are
a)
12, 18
b)
16, 4
c)
15, 5
d)
20, 5
|
Arjun Unni answered |
Let the numbers be a and b Then
Solving a + b = 20 and a - b = 12 we get a = 16 and b = 4.
then the value of x is
Find the Eigenvalues of matrix
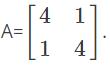
- a)8, 2
- b)3, -3
- c)-3, -5
- d)5, 0
Correct answer is option 'A'. Can you explain this answer?
Find the Eigenvalues of matrix
a)
8, 2
b)
3, -3
c)
-3, -5
d)
5, 0
|
|
Sanya Agarwal answered |
A - λI = 0
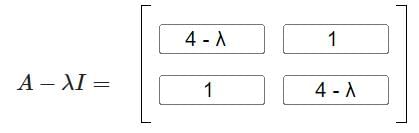
Now, After taking the determinant:
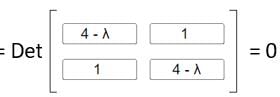
(4 - λ)2 - 1 = 0
16 + λ2 - 8λ - 1 = 0
λ2 - 8λ + 15 = 0
(λ
- 3) (
λ - 5) = 0
λ
= 3, 5
If a square matrix A is real and symmetric, then the eigenvaluesn - a)Are always real
- b)Are always real and positive
- c)Are always real and non-negative
- d)Occur in complex conjugate pairs
Correct answer is option 'A'. Can you explain this answer?
If a square matrix A is real and symmetric, then the eigenvaluesn
a)
Are always real
b)
Are always real and positive
c)
Are always real and non-negative
d)
Occur in complex conjugate pairs
|
Ishani Basu answered |
Real and Symmetric Square Matrix
A square matrix is a matrix with an equal number of rows and columns. In this case, we are considering a real and symmetric square matrix. A real matrix is a matrix that consists of real numbers as its elements, while a symmetric matrix is a matrix that is equal to its transpose.
Eigenvalues of a Matrix
Eigenvalues are a special set of scalars associated with a linear system of equations represented by a matrix. In other words, they are values that satisfy the equation Av = λv, where A is the matrix, λ is the eigenvalue, and v is the eigenvector.
Properties of Real and Symmetric Square Matrix
Real and symmetric square matrices have some specific properties that help determine the nature of their eigenvalues. These properties are:
1. Real Eigenvalues: Eigenvalues of a real matrix are always real numbers. This means that they do not have any imaginary components. Therefore, option 'a' is correct.
2. Orthogonal Eigenvectors: Real and symmetric matrices have orthogonal eigenvectors. Orthogonal vectors are perpendicular to each other, and their dot product is zero. This property helps in diagonalizing the matrix.
3. Diagonalization: Real and symmetric matrices can always be diagonalized. Diagonalization means transforming the matrix into a diagonal matrix by using the eigenvectors as transformation matrices. This process helps in simplifying calculations involving the matrix.
4. Positive Definiteness: Real and symmetric matrices can have positive eigenvalues, negative eigenvalues, or zero eigenvalues depending on their characteristics. However, it is not always true that the eigenvalues are positive. Therefore, option 'b' is incorrect.
5. Complex Conjugate Pairs: Complex conjugate pairs occur in matrices that are not real and symmetric. In the case of real and symmetric matrices, the eigenvalues are always real and do not occur in complex conjugate pairs. Therefore, option 'd' is incorrect.
Conclusion
In conclusion, if a square matrix is real and symmetric, its eigenvalues are always real. This is because real and symmetric matrices have specific properties that guarantee real eigenvalues. These properties include real eigenvalues, orthogonal eigenvectors, diagonalization, and the absence of complex conjugate pairs.
A square matrix is a matrix with an equal number of rows and columns. In this case, we are considering a real and symmetric square matrix. A real matrix is a matrix that consists of real numbers as its elements, while a symmetric matrix is a matrix that is equal to its transpose.
Eigenvalues of a Matrix
Eigenvalues are a special set of scalars associated with a linear system of equations represented by a matrix. In other words, they are values that satisfy the equation Av = λv, where A is the matrix, λ is the eigenvalue, and v is the eigenvector.
Properties of Real and Symmetric Square Matrix
Real and symmetric square matrices have some specific properties that help determine the nature of their eigenvalues. These properties are:
1. Real Eigenvalues: Eigenvalues of a real matrix are always real numbers. This means that they do not have any imaginary components. Therefore, option 'a' is correct.
2. Orthogonal Eigenvectors: Real and symmetric matrices have orthogonal eigenvectors. Orthogonal vectors are perpendicular to each other, and their dot product is zero. This property helps in diagonalizing the matrix.
3. Diagonalization: Real and symmetric matrices can always be diagonalized. Diagonalization means transforming the matrix into a diagonal matrix by using the eigenvectors as transformation matrices. This process helps in simplifying calculations involving the matrix.
4. Positive Definiteness: Real and symmetric matrices can have positive eigenvalues, negative eigenvalues, or zero eigenvalues depending on their characteristics. However, it is not always true that the eigenvalues are positive. Therefore, option 'b' is incorrect.
5. Complex Conjugate Pairs: Complex conjugate pairs occur in matrices that are not real and symmetric. In the case of real and symmetric matrices, the eigenvalues are always real and do not occur in complex conjugate pairs. Therefore, option 'd' is incorrect.
Conclusion
In conclusion, if a square matrix is real and symmetric, its eigenvalues are always real. This is because real and symmetric matrices have specific properties that guarantee real eigenvalues. These properties include real eigenvalues, orthogonal eigenvectors, diagonalization, and the absence of complex conjugate pairs.
s one of the eigen values is equal to -2. Which of the following is an eigen vector? 
The eigen values and the corresponding eigen vectors of a 2 × 2 matrix are given by
- a)
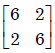
- b)
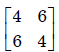
- c)
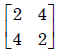
- d)
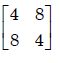
Correct answer is option 'A'. Can you explain this answer?
The eigen values and the corresponding eigen vectors of a 2 × 2 matrix are given by
a)
b)
c)
d)
|
Subodh Sharma answered |
Trace = sum of diagonal elements = sum of eigen value = 12
Only option (a) is satisfied.
Only option (a) is satisfied.
then top row of R-1 is 
The maximum value of f ( x) = (1 + cos x) sin x is- a)3
- b)3√3
- c)4
- d)3√3/4
Correct answer is option 'D'. Can you explain this answer?
The maximum value of f ( x) = (1 + cos x) sin x is
a)
3
b)
3√3
c)
4
d)
3√3/4
|
|
Radhika Sharma answered |
The given function is:
f(x) = (1 - cos(x))sin(x)
To find the maximum value of the function:
We can find the maximum value of the function by finding the critical points and determining whether they are maximum or minimum points.
Finding the critical points:
The critical points occur when the derivative of the function is zero or undefined. Let's find the derivative of the given function.
f'(x) = (1 - cos(x))cos(x) + sin(x)(-sin(x))
= cos(x) - cos^2(x) - sin^2(x)
= cos(x) - (1 - sin^2(x))
= cos(x) - 1 + sin^2(x)
= sin^2(x) + cos(x) - 1
Simplifying the derivative:
To find the critical points, we need to solve the equation f'(x) = 0.
sin^2(x) + cos(x) - 1 = 0
Using the identity sin^2(x) = 1 - cos^2(x):
1 - cos^2(x) + cos(x) - 1 = 0
Simplifying further:
-cos^2(x) + cos(x) = 0
Factoring out cos(x):
cos(x)(-cos(x) + 1) = 0
Setting each factor to zero:
cos(x) = 0 or -cos(x) + 1 = 0
Solving the first equation:
cos(x) = 0
This occurs when x = π/2 or x = 3π/2.
Solving the second equation:
-cos(x) + 1 = 0
cos(x) = 1
This occurs when x = 0 or x = 2π.
Therefore, the critical points are x = π/2, 3π/2, 0, and 2π.
Determining the nature of critical points:
To determine whether the critical points are maximum or minimum points, we can use the second derivative test. Let's find the second derivative of the function.
f''(x) = d/dx (sin^2(x) + cos(x) - 1)
= 2sin(x)cos(x) - sin(x)
Using the identity 2sin(x)cos(x) = sin(2x):
f''(x) = sin(2x) - sin(x)
Simplifying the second derivative:
f''(x) = 2sin(x)cos(x) - sin(x)
= sin(x)(2cos(x) - 1)
Evaluating the second derivative at the critical points:
f''(π/2) = sin(π/2)(2cos(π/2) - 1)
= 1(2(0) - 1)
= -1
f''(3π/2) = sin(3π/2)(2cos(3π/2) - 1)
= -1(2(0) - 1)
= 1
f''(0
f(x) = (1 - cos(x))sin(x)
To find the maximum value of the function:
We can find the maximum value of the function by finding the critical points and determining whether they are maximum or minimum points.
Finding the critical points:
The critical points occur when the derivative of the function is zero or undefined. Let's find the derivative of the given function.
f'(x) = (1 - cos(x))cos(x) + sin(x)(-sin(x))
= cos(x) - cos^2(x) - sin^2(x)
= cos(x) - (1 - sin^2(x))
= cos(x) - 1 + sin^2(x)
= sin^2(x) + cos(x) - 1
Simplifying the derivative:
To find the critical points, we need to solve the equation f'(x) = 0.
sin^2(x) + cos(x) - 1 = 0
Using the identity sin^2(x) = 1 - cos^2(x):
1 - cos^2(x) + cos(x) - 1 = 0
Simplifying further:
-cos^2(x) + cos(x) = 0
Factoring out cos(x):
cos(x)(-cos(x) + 1) = 0
Setting each factor to zero:
cos(x) = 0 or -cos(x) + 1 = 0
Solving the first equation:
cos(x) = 0
This occurs when x = π/2 or x = 3π/2.
Solving the second equation:
-cos(x) + 1 = 0
cos(x) = 1
This occurs when x = 0 or x = 2π.
Therefore, the critical points are x = π/2, 3π/2, 0, and 2π.
Determining the nature of critical points:
To determine whether the critical points are maximum or minimum points, we can use the second derivative test. Let's find the second derivative of the function.
f''(x) = d/dx (sin^2(x) + cos(x) - 1)
= 2sin(x)cos(x) - sin(x)
Using the identity 2sin(x)cos(x) = sin(2x):
f''(x) = sin(2x) - sin(x)
Simplifying the second derivative:
f''(x) = 2sin(x)cos(x) - sin(x)
= sin(x)(2cos(x) - 1)
Evaluating the second derivative at the critical points:
f''(π/2) = sin(π/2)(2cos(π/2) - 1)
= 1(2(0) - 1)
= -1
f''(3π/2) = sin(3π/2)(2cos(3π/2) - 1)
= -1(2(0) - 1)
= 1
f''(0
The eigen values of a skew-symmetric matrix are- a)Always zero
- b)always pure imaginary
- c)Either zero or pure imaginary
- d)always real
Correct answer is option 'C'. Can you explain this answer?
The eigen values of a skew-symmetric matrix are
a)
Always zero
b)
always pure imaginary
c)
Either zero or pure imaginary
d)
always real
|
Byomkesh Kamila answered |
Here,(a_ij)=-(a_ji)#for all diagonal elements,a_ij=a_ii =a_jj.
a_ii=-a_ii#2a_ii=0#a_ii=0/2=0 for all values of i≤n.
a_ii=-a_ii#2a_ii=0#a_ii=0/2=0 for all values of i≤n.
The system of linear equations
4x + 2y = 7
2x + y = 6 has
- a)A unique solution
- b)no solution
- c)An infinite number of solutions
- d)exactly two distinct solutions
Correct answer is option 'B'. Can you explain this answer?
The system of linear equations
4x + 2y = 7
2x + y = 6 has
4x + 2y = 7
2x + y = 6 has
a)
A unique solution
b)
no solution
c)
An infinite number of solutions
d)
exactly two distinct solutions
|
|
Rhea Reddy answered |
(b) This can be written as AX = B Where A
Angemented matrix
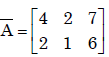
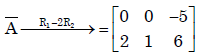
rank(A) ≠ rank(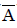
). The system is inconsistant .So system has no solution.
). The system is inconsistant .So system has no solution.For the following set of simultaneous equations:
1.5x – 0.5y = 2
4x + 2y + 3z = 9
7x + y + 5z = 10 - a)The solution is unique
- b)Infinitely many solutions exist
- c)The equations are incompatible
- d)Finite number of multiple solutions exist
Correct answer is option 'A'. Can you explain this answer?
For the following set of simultaneous equations:
1.5x – 0.5y = 2
4x + 2y + 3z = 9
7x + y + 5z = 10
1.5x – 0.5y = 2
4x + 2y + 3z = 9
7x + y + 5z = 10
a)
The solution is unique
b)
Infinitely many solutions exist
c)
The equations are incompatible
d)
Finite number of multiple solutions exist
|
|
Dipika Nambiar answered |
(a)
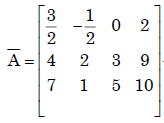
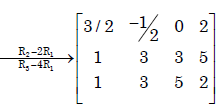
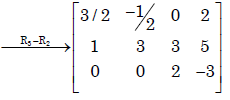
∴ rank of(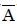
) = rank of(A) = 3
) = rank of(A) = 3∴ The system has unique solution.
Select a suitable figure from the four alternatives that would complete the figure matrix.
- a) 1
- b) 2
- c) 3
- d)4
Correct answer is option 'D'. Can you explain this answer?
Select a suitable figure from the four alternatives that would complete the figure matrix.
a)
1
b)
2
c)
3
d)
4
|
|
Kiran Datta answered |
In each row (as well as each column), the third figure is a combination of all the, elements of the first and the second figures
is,
Chapter doubts & questions for Engineering Mathematics - GATE Electrical Engineering (EE) Mock Test Series 2026 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Engineering Mathematics - GATE Electrical Engineering (EE) Mock Test Series 2026 in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
GATE Electrical Engineering (EE) Mock Test Series 2026
25 docs|247 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup