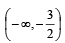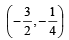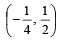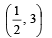All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Quadratic Equation and Inequations (Inequalities) for JEE Exam
Let 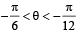 Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)
Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)- a)2 (secθ – tanθ)
- b)2 secθ
- c)–2 tanθ
- d)0
Correct answer is option 'C'. Can you explain this answer?
Let 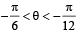 Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)
Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)
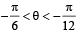 Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)
Suppose α1 and B1are the roots of the equation x2 – 2x sec a + 1 = 0 and α2 and β2 are the roots of the equation x2 + 2x tanθ – 1 = 0. If α1 > b1 and α2 > β2, then α1 + β2 equals (JEE Adv. 2016)a)
2 (secθ – tanθ)
b)
2 secθ
c)
–2 tanθ
d)
0
|
|
Krishna Iyer answered |
x2 – 2x secθ + 1 = 0 ⇒ x = secθ ± tanθ and x2 + 2x tanθ – 1 = 0 ⇒ x = –tanθ ± secθ
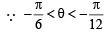
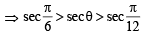
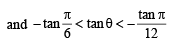
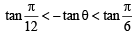
α1,β1 are roots of x2 – 2x secθ + 1 = 0 and α1> b1
∴ α1 = secθ – tanθ and b1 = secθ + tanθ α2,
β2 are roots of x2 + 2x tanθ – 1 = 0 and α2 > β2
∴ α2 = -tanθ + secθ, β2 = – tanθ – secθ
∴ α1 + β2 = secθ – tanθ – tanθ – secθ = – 2tanθ
β2 are roots of x2 + 2x tanθ – 1 = 0 and α2 > β2
∴ α2 = -tanθ + secθ, β2 = – tanθ – secθ
∴ α1 + β2 = secθ – tanθ – tanθ – secθ = – 2tanθ
Let (x0, y0) be the solution of the following equations
(2x)ℓn2 = (3y)ℓn3
3ℓnx =2ℓny
Then x0 is (2011)- a)
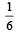
- b)
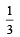
- c)
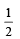
- d)6
Correct answer is option 'C'. Can you explain this answer?
Let (x0, y0) be the solution of the following equations
(2x)ℓn2 = (3y)ℓn3
3ℓnx =2ℓny
Then x0 is (2011)
(2x)ℓn2 = (3y)ℓn3
3ℓnx =2ℓny
Then x0 is (2011)
a)
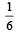
b)
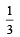
c)
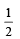
d)
6

|
Manish Aggarwal answered |
We have (2x)ℓn2 = (3y)ℓn3
⇒ ℓn2. ℓn2x = ℓn3. ℓn3y
⇒ ℓn2. ℓn2x = ℓn3. (ℓn3 + ℓny) ...(1)
Also given 3ℓnx = 2lny
⇒ ℓn2. ℓn2x = ℓn3. ℓn3y
⇒ ℓn2. ℓn2x = ℓn3. (ℓn3 + ℓny) ...(1)
Also given 3ℓnx = 2lny
⇒ ℓnx. ℓn3 = ℓny. ℓn2 ⇒ ℓny = 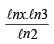
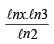
Substituting this value of ℓny in equation (1), we get
ℓn2. ℓn2x = ℓn3 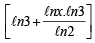
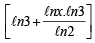
⇒ (ℓn2)2 ℓn2x = (ℓn3)2 ℓn2 + (ℓn3)2 ℓnx
⇒ (ℓn2)2 ℓn2x = (ℓn3)2 (ℓn2 + ℓnx)
⇒ (ℓn2)2 ℓn2x – (ℓn3)2 ℓn2x = 0
⇒ [(ℓn2)2 – (ℓn3)2] ℓn2x = 0 ⇒ ℓn2x = 0
⇒ 2x = 1 or x = 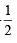
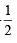
If p, q, r are +ve and are in A.P., the roots of quadratic equation px2 + qx + r = 0 are all real for (1994)- a)

- b)
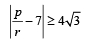
- c)all p and r
- d)no p an d r
Correct answer is option 'B'. Can you explain this answer?
If p, q, r are +ve and are in A.P., the roots of quadratic equation px2 + qx + r = 0 are all real for (1994)
a)

b)
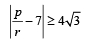
c)
all p and r
d)
no p an d r
|
|
Geetika Shah answered |
For real roots q2 - 4 pr≥0
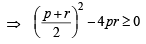 (∵ p, q, r are in A.P.)
(∵ p, q, r are in A.P.)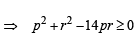
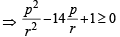
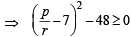
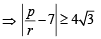
If α and β (α < β) are the roots of the equation x2 + bx + c = 0, where c < 0 < β, then (2000S)- a)0 < α < β
- b)α < 0 < β < | α |
- c)α < β < 0
- d)α < 0 < | α | < β
Correct answer is option 'B'. Can you explain this answer?
If α and β (α < β) are the roots of the equation x2 + bx + c = 0, where c < 0 < β, then (2000S)
a)
0 < α < β
b)
α < 0 < β < | α |
c)
α < β < 0
d)
α < 0 < | α | < β
|
|
Chirag Verma answered |
Given c < 0 < b and α + β = – b ....(1) αβ = c
....(2)
....(2)
From (2), c < 0 ⇒ αβ < 0 ⇒ either a is -ve or β is - ve and second ;quantity is positive.
from (1), b > 0 ⇒ – b < 0 ⇒ α + β < 0 ⇒ the sum is negative
⇒ modules of nengative quantity is > modulus of positive quantity but α< β is given.
Therefore, it is clear that α is negative and β is positive and modulus of α is greater than modulus of β ⇒ α< 0 <β< |α|
Therefore, it is clear that α is negative and β is positive and modulus of α is greater than modulus of β ⇒ α< 0 <β< |α|
Let a, b, c be the sides of a triangle where a ≠ b ≠ c and λ ∈ R. If the roots of the equation x2 + 2(a + b + c)x + 3λ (ab + bc + ca) = 0 are real, then (2006 - 3M, –1)- a)

- b)
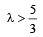
- c)
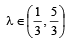
- d)
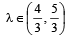
Correct answer is option 'A'. Can you explain this answer?
Let a, b, c be the sides of a triangle where a ≠ b ≠ c and λ ∈ R. If the roots of the equation x2 + 2(a + b + c)x + 3λ (ab + bc + ca) = 0 are real, then (2006 - 3M, –1)
a)

b)
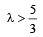
c)
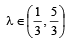
d)
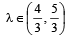
|
|
Chirag Verma answered |
∵ a, b, c are sides of a triangle and a ≠ b≠c
∴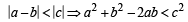
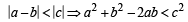
Similarly, we have
b2 + c2 - 2bc < a2 ; c2 + a2 -2ca<b2
On adding, we get
a2 + b2 + c2 < 2(ab + bc+ ca)
 ....(1)
....(1)∵ Roots of the given equation are real
∴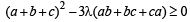
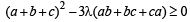
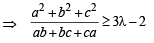 ....(2)
....(2)From (1) and (2), we get 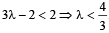
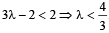
The sum of all real values of x satisfying the equation (x2 - 5 x+ 5) x2 +4x- 60 = 1 is : [JEE M 2016]- a)6
- b)5
- c)3
- d)– 4
Correct answer is option 'C'. Can you explain this answer?
The sum of all real values of x satisfying the equation (x2 - 5 x+ 5) x2 +4x- 60 = 1 is : [JEE M 2016]
a)
6
b)
5
c)
3
d)
– 4
|
|
Ananya Das answered |
(x2 - 5 x + 5) x2 + 4x-60=1
Case I x2 – 5x + 5 = 1 and
x2 + 4x – 60 can be any real number
⇒ x = 1, 4
Case II x2 – 5x + 5 = –1 and
x2 + 4x – 60 has to be an even number
⇒ x = 2, 3 where 3 is rejected because for x = 3,
x2 + 4x – 60 is odd.
Case III x2 – 5x + 5 can be any real number and
x2 + 4x – 60 = 0
⇒ x = –10, 6
⇒ Sum of all values of x = –10 + 6 + 2 + 1 + 4 = 3
Case I x2 – 5x + 5 = 1 and
x2 + 4x – 60 can be any real number
⇒ x = 1, 4
Case II x2 – 5x + 5 = –1 and
x2 + 4x – 60 has to be an even number
⇒ x = 2, 3 where 3 is rejected because for x = 3,
x2 + 4x – 60 is odd.
Case III x2 – 5x + 5 can be any real number and
x2 + 4x – 60 = 0
⇒ x = –10, 6
⇒ Sum of all values of x = –10 + 6 + 2 + 1 + 4 = 3
If the roots of the equation x2 – 2ax + a2 + a – 3 = 0 are real and less than 3, then (1999 - 2 Marks)- a)a < 2
- b)2 ≤ a ≤ 3
- c)3 < a ≤ 4
- d)a > 4
Correct answer is option 'A'. Can you explain this answer?
If the roots of the equation x2 – 2ax + a2 + a – 3 = 0 are real and less than 3, then (1999 - 2 Marks)
a)
a < 2
b)
2 ≤ a ≤ 3
c)
3 < a ≤ 4
d)
a > 4
|
|
Geetika Shah answered |
KEY CONCEPT : If both roots of a quadratic equation ax2 + bx + c = 0 are less than k then af(k)
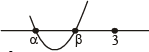
> 0, D ≥ 0, α + β < 2 k.
f(x) = x2 – 2ax + a2 + a – 3 = 0,
f(3) > 0, α + β < 6, D ≥ 0
⇒ a2 – 5a + 6 > 0, a < 3, – 4a + 12 ≥ 0
⇒ a < 2 or a > 3, a < 3, a < 3 ⇒ a < 2.
The quadritic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is [2009]- a)1
- b)4
- c)3
- d)2
Correct answer is option 'D'. Can you explain this answer?
The quadritic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is [2009]
a)
1
b)
4
c)
3
d)
2
|
|
Chirag Verma answered |
Let the roots of equation x2 – 6x + α = 0 be α and 4 β and that of the equation
x2 –cx + 6 = 0 be α and 3β .
Then α + 4β = 6 ; 4aβ = α and α + 3β = c ; 3αβ = 6
⇒ α = 8
∴ The equation becomes x2 – 6x + 8 = 0
⇒ (x –2) (x – 4) = 0
⇒ roots are 2 and 4 ⇒ α = 2, β = 1
∴ Common root is 2.
x2 –cx + 6 = 0 be α and 3β .
Then α + 4β = 6 ; 4aβ = α and α + 3β = c ; 3αβ = 6
⇒ α = 8
∴ The equation becomes x2 – 6x + 8 = 0
⇒ (x –2) (x – 4) = 0
⇒ roots are 2 and 4 ⇒ α = 2, β = 1
∴ Common root is 2.
Two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school should be built at (1982 - 2 Marks)- a)town B
- b)45 km from town A
- c)town A
- d)45 km from town B
Correct answer is option 'C'. Can you explain this answer?
Two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school should be built at (1982 - 2 Marks)
a)
town B
b)
45 km from town A
c)
town A
d)
45 km from town B
|
|
Lavanya Menon answered |
Let the distance of school from A = x
∴ The distance of the school form B = 60 – x
Total distance covered by 200 students = 2[150 x + 50 (60 – x) ] = 2[100 x + 3000] This is min., when x = 0
∴ school should be built at town A.
∴ The distance of the school form B = 60 – x
Total distance covered by 200 students = 2[150 x + 50 (60 – x) ] = 2[100 x + 3000] This is min., when x = 0
∴ school should be built at town A.
If α and β are the roots of x2 + px + q = 0 and α4, β4 are the roots of x2 – rx + s = 0, then the equation x2 – 4qx + 2q2 – r = 0 has always (1989 - 2 Marks)- a)two real roots
- b)two positive roots
- c)two negative roots
- d)one positive and one negative root
Correct answer is option 'D'. Can you explain this answer?
If α and β are the roots of x2 + px + q = 0 and α4, β4 are the roots of x2 – rx + s = 0, then the equation x2 – 4qx + 2q2 – r = 0 has always (1989 - 2 Marks)
a)
two real roots
b)
two positive roots
c)
two negative roots
d)
one positive and one negative root
|
|
Ram Mohith answered |

If a, b, c, d and p are distinct real numbers such that (a2 + b2 + c2)p2 – 2 (ab + bc + cd)p + (b2 + c2 + d2) ≤ 0 then a, b, c, d (1987 - 2 Marks)- a)are in A. P.
- b)are in G. P.
- c)are in H. P.
- d)satisfy ab = cd
- e)satisfy none of these
Correct answer is option 'B'. Can you explain this answer?
If a, b, c, d and p are distinct real numbers such that (a2 + b2 + c2)p2 – 2 (ab + bc + cd)p + (b2 + c2 + d2) ≤ 0 then a, b, c, d (1987 - 2 Marks)
a)
are in A. P.
b)
are in G. P.
c)
are in H. P.
d)
satisfy ab = cd
e)
satisfy none of these
|
|
Nishanth Joshi answered |
Given that a, b, c, d, p are real and distinct numbers such that
(a2 + b2 + c2) p2 - 2(ab + bc + cd) p + (b2 + c2 +d2)≤0
⇒ (a2 p2 + b2 p2 + c2 p2 ) - (2abp + 2bcp+ 2cdp) +(b2 + c2 +d2 )≤0
⇒ (a2 p2 - 2abp + b2) + (b2 p2 - 2bcp+ c2) +(c2 p2 - 2cdp +d2 )≤0
⇒ (ap - b)2 + (bp - c)2 + (cp - d)2 ≤ 0
Being sum of perfect squares, LHS can never be –ve, therefore the only possibility is
(ap - b)2 + (bp - c)2 + (cp -d )2=0
Which is possible only when each term is zero individually i.e.
ap -b = 0; bp -c = 0; cp - d=0
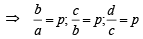

⇒ a,b,c,d are in G.P.
The real number x when added to its inverse gives the minimum value of the sum at x equal to [2003]- a) –2
- b) 2
- c) 1
- d) –1
Correct answer is option 'C'. Can you explain this answer?
The real number x when added to its inverse gives the minimum value of the sum at x equal to [2003]
a)
–2
b)
2
c)
1
d)
–1
|
|
Srestha Basak answered |
 or
or 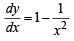
For max. or min., 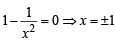
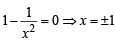
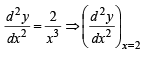 = 2(+ve minima) ∴x = 1
= 2(+ve minima) ∴x = 1Product of real roots of the equation t2x2+|x|+9=0 [2002]- a)is always positive
- b)is always negative
- c)does not exist
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Product of real roots of the equation t2x2+|x|+9=0 [2002]
a)
is always positive
b)
is always negative
c)
does not exist
d)
none of these
|
|
Ritika Sen answered |
Product of real roots = 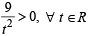
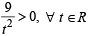
∴ Product of real roots is always positive.
The equation x + 2y + 2z = 1 and 2x + 4y + 4z = 9 have- a)Only one solution (1979)
- b)Only two solutions
- c)Infinite number of solutions
- d)None of these.
Correct answer is option 'D'. Can you explain this answer?
The equation x + 2y + 2z = 1 and 2x + 4y + 4z = 9 have
a)
Only one solution (1979)
b)
Only two solutions
c)
Infinite number of solutions
d)
None of these.
|
|
Aarya Shah answered |
The given equations are
x + 2y + 2z = 1 ....(1)
and 2x + 4y + 4z = 9 ....(2)
Subtracting (1) × (2) from (2),
we get 0 =7 (not possible)
∴ No solution.
x + 2y + 2z = 1 ....(1)
and 2x + 4y + 4z = 9 ....(2)
Subtracting (1) × (2) from (2),
we get 0 =7 (not possible)
∴ No solution.
Difference between the corresponding roots of x2+ax+b=0 and x2+bx+a=0 is same and a ≠ b, then [2002]- a)a + b + 4 = 0
- b)a + b – 4 = 0
- c)a – b – 4 = 0
- d)a – b + 4 = 0
Correct answer is option 'A'. Can you explain this answer?
Difference between the corresponding roots of x2+ax+b=0 and x2+bx+a=0 is same and a ≠ b, then [2002]
a)
a + b + 4 = 0
b)
a + b – 4 = 0
c)
a – b – 4 = 0
d)
a – b + 4 = 0
|
|
Shreya Saha answered |
Let α, β and γ, δ be the roots of the equations
x2 + αx + β = 0 and
x2 + βx + α = 0 respectively.
∴ α + β = –α, αβ = β and γ + δ = –β, γ δ = α.
Given |α – β| = |γ – δ|
⇒ (α – β)2 = (γ – δ)2
⇒ (α + β)2 – 4αβ = (γ + δ)2 – 4γδ
⇒ α2 – 4β = β2 – 4α
⇒ (α2 – β2) + 4(α – β) = 0
⇒ α + β + 4 = 0 (∵ α ≠ β)
x2 + αx + β = 0 and
x2 + βx + α = 0 respectively.
∴ α + β = –α, αβ = β and γ + δ = –β, γ δ = α.
Given |α – β| = |γ – δ|
⇒ (α – β)2 = (γ – δ)2
⇒ (α + β)2 – 4αβ = (γ + δ)2 – 4γδ
⇒ α2 – 4β = β2 – 4α
⇒ (α2 – β2) + 4(α – β) = 0
⇒ α + β + 4 = 0 (∵ α ≠ β)
If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a,b,c ∈ R, have a common root, then a : b : c is [JEE M 2013]- a)1 : 2 : 3
- b)3 : 2 : 1
- c)1 : 3 : 2
- d)3 : 1 : 2
Correct answer is option 'A'. Can you explain this answer?
If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a,b,c ∈ R, have a common root, then a : b : c is [JEE M 2013]
a)
1 : 2 : 3
b)
3 : 2 : 1
c)
1 : 3 : 2
d)
3 : 1 : 2
|
|
Harsh Singhal answered |
First eq.has imaginary roots that is both eq.has both equal root so their stoichiometric coff.are in same ratio
If α ≠ β but α2 = 5α – 3 and β2 = 5β – 3 then the equation having α/β and β/α as its roots is [2002]- a)3x2 – 19x + 3 = 0
- b)3x2 + 19x – 3 = 0
- c)3x2 – 19x – 3 = 0
- d)x2 – 5x + 3 = 0.
Correct answer is option 'A'. Can you explain this answer?
If α ≠ β but α2 = 5α – 3 and β2 = 5β – 3 then the equation having α/β and β/α as its roots is [2002]
a)
3x2 – 19x + 3 = 0
b)
3x2 + 19x – 3 = 0
c)
3x2 – 19x – 3 = 0
d)
x2 – 5x + 3 = 0.
|
|
Nitya Sarkar answered |
If I were a bird, I would fly high in the sky, exploring new places and enjoying the freedom of flight. I would soar above mountains, glide over oceans, and visit different countries. I would build a nest in a tree and sing beautiful songs to communicate with other birds. I would also enjoy the feeling of the wind rushing through my feathers and the breathtaking views from above. Overall, being a bird would be a thrilling and exhilarating experience.
The equation 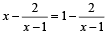 has (1984 - 2 Marks)
has (1984 - 2 Marks) - a)no root
- b)one root
- c)two equal roots
- d)infinitely many roots
Correct answer is option 'A'. Can you explain this answer?
The equation 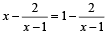 has (1984 - 2 Marks)
has (1984 - 2 Marks)
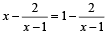 has (1984 - 2 Marks)
has (1984 - 2 Marks) a)
no root
b)
one root
c)
two equal roots
d)
infinitely many roots
|
|
Anand Kumar answered |
If X= 1 then given function will be undefine.
so, X not equal to 1
i.e, no solution exist for the given function
so, X not equal to 1
i.e, no solution exist for the given function
The number of poin ts of intersection of two curves y = 2 sinx and y = 5x2 + 2x + 3 is (1994)- a)0
- b)1
- c)2
- d)∞
Correct answer is option 'A'. Can you explain this answer?
The number of poin ts of intersection of two curves y = 2 sinx and y = 5x2 + 2x + 3 is (1994)
a)
0
b)
1
c)
2
d)
∞
|
|
Deepak Kumar answered |
We have 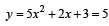
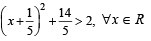
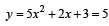
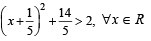
while y = 
⇒ The two curves do not meet at all.
If a2 + b2 + c2 = 1, then ab + bc + ca lies in the interval (1984 - 2 Marks)- a)
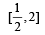
- b) [–1, 2]
- c)
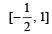
- d)
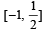
Correct answer is option 'C'. Can you explain this answer?
If a2 + b2 + c2 = 1, then ab + bc + ca lies in the interval (1984 - 2 Marks)
a)
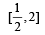
b)
[–1, 2]
c)
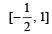
d)
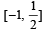
|
|
Anaya Patel answered |
Given that a2 + b2 + c2 = 1 ....(1) We know (a + b +c)2 ≥ 0
⇒ a2 + b2 + c2 + 2ab + 2bc + 2ca ≥ 0
⇒ 2 ( ab + bc + c a ) ≥-1 [Using (1)]
⇒ ab + bc + ca ≥-1 / 2....(2) ....(2) Also we know that
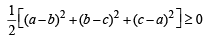
Þ a2 + b2 + c2- ab- bc - ca≥ 0
Þ ab + bc + ca ≤ 1 [Using (1)] .......(2)
Combining (2) and (3), we get
-1/ 2 ≤ ab + bc + ca≤1 ∴ab + bc + ca ∈ [-1/ 2,1]
∴ (c) is the correct answer.
The least value of the expression 2 log10x – logx(0.01), for x > 1, is(1980)- a)10
- b)2
- c)– 0.01
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
The least value of the expression 2 log10x – logx(0.01), for x > 1, is(1980)
a)
10
b)
2
c)
– 0.01
d)
none of these.
|
|
Mahi Sarkar answered |
The least value of the expression 2 log10x occurs when x = 1, because log10(1) = 0.
Therefore, the least value of the expression 2 log10x is 2(0) = 0.
Therefore, the least value of the expression 2 log10x is 2(0) = 0.
If x, y and z are real and different and (1979) u = x2 + 4y2 + 9z2 – 6yz – 3zx – 2xy, then u is always.- a)non negative
- b)zero
- c)non positive
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If x, y and z are real and different and (1979) u = x2 + 4y2 + 9z2 – 6yz – 3zx – 2xy, then u is always.
a)
non negative
b)
zero
c)
non positive
d)
none of these
|
|
Shraddha Roy answered |
u = x2 + 4y2 + 9z2 – 6yx – 3zx – 2xy
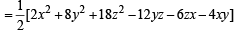
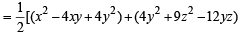
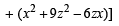
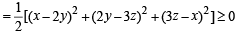
∴ u is always non-negative.
If a, b and c are distinct positive numbers, then the expression (b + c – a)(c + a – b)(a + b – c) – abc is (1986 - 2 Marks)- a)positive
- b)negative
- c)non-positive
- d)non -negative
- e)none of these
Correct answer is option 'B'. Can you explain this answer?
If a, b and c are distinct positive numbers, then the expression (b + c – a)(c + a – b)(a + b – c) – abc is (1986 - 2 Marks)
a)
positive
b)
negative
c)
non-positive
d)
non -negative
e)
none of these
|
|
Ruchi Tiwari answered |
We can simplify the given expression as follows:
(b + c - a)(c + a - b)(a + b - c)
Using the identity (x + y - z)^2 = x^2 + y^2 + z^2 + 2xy - 2xz - 2yz, we can expand each of the three factors in the expression:
(b + c - a)^2 = b^2 + c^2 + a^2 + 2bc - 2ab - 2ac
(c + a - b)^2 = c^2 + a^2 + b^2 + 2ca - 2cb - 2ab
(a + b - c)^2 = a^2 + b^2 + c^2 + 2ab - 2ac - 2bc
Adding these three expressions and simplifying, we get:
2(a^2 + b^2 + c^2) + 2(ab + ac + bc) - (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)
= a^2 + b^2 + c^2 - 2ab - 2ac - 2bc
= (a - b)^2 + (a - c)^2 + (b - c)^2
This is always non-negative, and is equal to zero if and only if a = b = c. Therefore, the given expression is positive for all distinct positive numbers a, b, and c.
(b + c - a)(c + a - b)(a + b - c)
Using the identity (x + y - z)^2 = x^2 + y^2 + z^2 + 2xy - 2xz - 2yz, we can expand each of the three factors in the expression:
(b + c - a)^2 = b^2 + c^2 + a^2 + 2bc - 2ab - 2ac
(c + a - b)^2 = c^2 + a^2 + b^2 + 2ca - 2cb - 2ab
(a + b - c)^2 = a^2 + b^2 + c^2 + 2ab - 2ac - 2bc
Adding these three expressions and simplifying, we get:
2(a^2 + b^2 + c^2) + 2(ab + ac + bc) - (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)
= a^2 + b^2 + c^2 - 2ab - 2ac - 2bc
= (a - b)^2 + (a - c)^2 + (b - c)^2
This is always non-negative, and is equal to zero if and only if a = b = c. Therefore, the given expression is positive for all distinct positive numbers a, b, and c.
If a ∈ R and the equation -3 ( x - [ x])2 + 2 ( x- [ x])+a 2 =0 (where [x] denotes the greatest integer ≤ x ) has no integral solution, then all possible values of a lie in the interval: [JEE M 2014]- a)( -2,-1)
- b)( -∞, -2 ) ∪ ( 2,∞ )
- c)( -1, 0 ) ∪ ( 0,1)
- d)(1,2 )
Correct answer is option 'C'. Can you explain this answer?
If a ∈ R and the equation -3 ( x - [ x])2 + 2 ( x- [ x])+a 2 =0 (where [x] denotes the greatest integer ≤ x ) has no integral solution, then all possible values of a lie in the interval: [JEE M 2014]
a)
( -2,-1)
b)
( -∞, -2 ) ∪ ( 2,∞ )
c)
( -1, 0 ) ∪ ( 0,1)
d)
(1,2 )
|
|
Athul Kapoor answered |
Consider –3(x – [x])2 + 2 [x – [x]) + a2 = 0
⇒ 3{x}2 – 2{x} –a2 = 0 (∵ x – [x] = {x})
⇒ 3{x}2 – 2{x} –a2 = 0 (∵ x – [x] = {x})
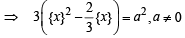
⇒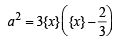
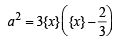
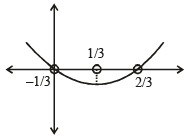
Now, {x} ∈ (0,1) and 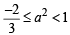 (by graph)
(by graph)
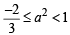 (by graph)
(by graph)Since , x is not an integer
∴ a ∈ (-1,1)- {0} ⇒ a ∈ (-1, 0)∪(0,1)
∴ a ∈ (-1,1)- {0} ⇒ a ∈ (-1, 0)∪(0,1)
All the values of m for which both roots of the equation x2 - 2mx +m2 - 1=0 are greater than – 2 but less then 4, lie in the interval [2006]- a)-2 < m<0
- b)m > 3
- c)-1 < m<3
- d)1 < m<4
Correct answer is option 'C'. Can you explain this answer?
All the values of m for which both roots of the equation x2 - 2mx +m2 - 1=0 are greater than – 2 but less then 4, lie in the interval [2006]
a)
-2 < m<0
b)
m > 3
c)
-1 < m<3
d)
1 < m<4
|
|
Subhankar Basu answered |
Equation x2 - 2mx +m2 - 1=0
(x -m)2 -1=0 or (x -m+1)(x -m-1)= 0
x = m - 1,m+1
m – 1 > –2 and m + 1<4
⇒ m >- 1 and m < 3 or,, -1 < m<3
(x -m)2 -1=0 or (x -m+1)(x -m-1)= 0
x = m - 1,m+1
m – 1 > –2 and m + 1<4
⇒ m >- 1 and m < 3 or,, -1 < m<3
If α and β are the roots of the equation x2 – x + 1 = 0, then α2009 + β2009 = [2010]- a)–1
- b)1
- c)2
- d)–2
Correct answer is option 'B'. Can you explain this answer?
If α and β are the roots of the equation x2 – x + 1 = 0, then α2009 + β2009 = [2010]
a)
–1
b)
1
c)
2
d)
–2
|
|
Anand Kumar answered |
Given equation has -w and -w^2 as roots (w = omega)
alpha = n = -w & beta = m= -w^2
n^2009 + m^2009 = (n^3)^669.n^2 + (m^3)^669.m^2
= (-w^3)^699.n^2 + ((-w^3)^2)^669.m^2
we know that w^3 = 1
therefore, = -n^2 - m^2
= -(n^2+m^2)
= -[(n+m)^2 - 2nm]
from the given equation n+m = 1 and nm= 1
= -(1-2) = 1
alpha = n = -w & beta = m= -w^2
n^2009 + m^2009 = (n^3)^669.n^2 + (m^3)^669.m^2
= (-w^3)^699.n^2 + ((-w^3)^2)^669.m^2
we know that w^3 = 1
therefore, = -n^2 - m^2
= -(n^2+m^2)
= -[(n+m)^2 - 2nm]
from the given equation n+m = 1 and nm= 1
= -(1-2) = 1
Number of divisor of the form 4n + 2 (n ≥ 0) of the integer 240 is (1998 - 2 Marks)- a)4
- b)8
- c)10
- d)3
Correct answer is option 'A'. Can you explain this answer?
Number of divisor of the form 4n + 2 (n ≥ 0) of the integer 240 is (1998 - 2 Marks)
a)
4
b)
8
c)
10
d)
3
|
|
Vaishnavi Chauhan answered |
We can start by noticing that any number of the form 4n+2 must have at least one factor of 2, since it is even. So we can write any such number as 2k, where k is an odd integer.
Now, let's consider the prime factorization of k. Since k is odd, it has no factors of 2. Therefore, any divisor of k must also be odd.
Next, we observe that any divisor of 2k must be of the form 2m or 2m+1, where m is an integer. If a divisor of k is of the form 2m, then the corresponding divisor of 2k is 4m. If a divisor of k is of the form 2m+1, then the corresponding divisor of 2k is 2(2m+1) = 4m+2.
Therefore, to count the number of divisors of 2k that are of the form 4n+2, we need to count the number of divisors of k that are odd and of the form 2m+1. Let's call this count d(k).
To find d(k), we can use the fact that the number of divisors of any integer n can be calculated using its prime factorization. If n = p1^a1 * p2^a2 * ... * pk^ak, then the number of divisors of n is (a1+1)(a2+1)...(ak+1).
Since k is odd, its prime factorization can be written as k = p1^a1 * p2^a2 * ... * pk^ak, where each ai is an integer and each pi is an odd prime. Therefore, the number of divisors of k is
d(k) = (a1+1)(a2+1)...(ak+1).
However, we only want to count the odd divisors of k that are of the form 2m+1. To do this, we can subtract the number of even divisors of k from the total number of divisors.
The number of even divisors of k is equal to the number of divisors of 2k (since each even divisor of k corresponds to a divisor of 2k by multiplying by 2), which is (a1+2)(a2+1)...(ak+1).
Therefore, the number of odd divisors of k that are of the form 2m+1 is
d(k) - (a1+2)(a2+1)...(ak+1).
Finally, to get the number of divisors of 2k that are of the form 4n+2, we need to multiply this count by 2 (since each odd divisor of k corresponds to two divisors of 2k that are of the form 4n+2, as we saw earlier).
Putting it all together, the number of divisors of 2k that are of the form 4n+2 is
2[d(k) - (a1+2)(a2+1)...(ak+1)].
Now, let's consider the prime factorization of k. Since k is odd, it has no factors of 2. Therefore, any divisor of k must also be odd.
Next, we observe that any divisor of 2k must be of the form 2m or 2m+1, where m is an integer. If a divisor of k is of the form 2m, then the corresponding divisor of 2k is 4m. If a divisor of k is of the form 2m+1, then the corresponding divisor of 2k is 2(2m+1) = 4m+2.
Therefore, to count the number of divisors of 2k that are of the form 4n+2, we need to count the number of divisors of k that are odd and of the form 2m+1. Let's call this count d(k).
To find d(k), we can use the fact that the number of divisors of any integer n can be calculated using its prime factorization. If n = p1^a1 * p2^a2 * ... * pk^ak, then the number of divisors of n is (a1+1)(a2+1)...(ak+1).
Since k is odd, its prime factorization can be written as k = p1^a1 * p2^a2 * ... * pk^ak, where each ai is an integer and each pi is an odd prime. Therefore, the number of divisors of k is
d(k) = (a1+1)(a2+1)...(ak+1).
However, we only want to count the odd divisors of k that are of the form 2m+1. To do this, we can subtract the number of even divisors of k from the total number of divisors.
The number of even divisors of k is equal to the number of divisors of 2k (since each even divisor of k corresponds to a divisor of 2k by multiplying by 2), which is (a1+2)(a2+1)...(ak+1).
Therefore, the number of odd divisors of k that are of the form 2m+1 is
d(k) - (a1+2)(a2+1)...(ak+1).
Finally, to get the number of divisors of 2k that are of the form 4n+2, we need to multiply this count by 2 (since each odd divisor of k corresponds to two divisors of 2k that are of the form 4n+2, as we saw earlier).
Putting it all together, the number of divisors of 2k that are of the form 4n+2 is
2[d(k) - (a1+2)(a2+1)...(ak+1)].
If a, b, c are distinct +ve real numbers and a2+b2+c2=1 then ab + bc + ca is [2002]- a)less than 1
- b)equal to 1
- c)greater than 1
- d)any real no.
Correct answer is option 'A'. Can you explain this answer?
If a, b, c are distinct +ve real numbers and a2+b2+c2=1 then ab + bc + ca is [2002]
a)
less than 1
b)
equal to 1
c)
greater than 1
d)
any real no.
|
|
Ashwin Pillai answered |
∵ (a – b)2 + (b – c)2 + (c – a)2 > 0
⇒ 2(a2 + b2 + c2 – ab – bc – ca) >0
⇒ 2 > 2(ab + bc + ca)
⇒ ab + bc + ca < 1
⇒ 2(a2 + b2 + c2 – ab – bc – ca) >0
⇒ 2 > 2(ab + bc + ca)
⇒ ab + bc + ca < 1
The number of real roots of the equation x2 - 3|x| + 2 = 0 is
- a) 3
- b) 2
- c) 4
- d) 1
Correct answer is option 'C'. Can you explain this answer?
The number of real roots of the equation x2 - 3|x| + 2 = 0 is
a)
3
b)
2
c)
4
d)
1
|
|
Arya Mishra answered |
**Solution:**
To find the number of real solutions of the equation x^2 - 3x + 2 = 0, we can use the discriminant.
The discriminant is given by the formula D = b^2 - 4ac, where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c = 0.
In this equation, a = 1, b = -3, and c = 2.
Substituting these values into the discriminant formula, we get:
D = (-3)^2 - 4(1)(2)
= 9 - 8
= 1
Since the discriminant is positive (D > 0), the equation has two distinct real solutions.
Therefore, the correct answer is option (b) 2.
**Explanation:**
The discriminant of a quadratic equation determines the number and nature of its solutions.
1. If the discriminant is positive (D > 0), the equation has two distinct real solutions.
2. If the discriminant is zero (D = 0), the equation has one real solution (also called a double root).
3. If the discriminant is negative (D < 0),="" the="" equation="" has="" no="" real="" solutions,="" but="" it="" may="" have="" complex="" />
In this case, the discriminant is positive (D = 1), so the equation x^2 - 3x + 2 = 0 has two distinct real solutions.
To find the values of x, we can use the quadratic formula:
x = (-b ± √D) / 2a
Substituting the values of a, b, and D into the formula, we get:
x = (-(-3) ± √1) / (2(1))
= (3 ± 1) / 2
Therefore, the two solutions are:
x1 = (3 + 1) / 2 = 4 / 2 = 2
x2 = (3 - 1) / 2 = 2 / 2 = 1
Hence, the equation x^2 - 3x + 2 = 0 has two real solutions: x = 1 and x = 2.
Therefore, the correct answer is option (b) 2.
To find the number of real solutions of the equation x^2 - 3x + 2 = 0, we can use the discriminant.
The discriminant is given by the formula D = b^2 - 4ac, where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c = 0.
In this equation, a = 1, b = -3, and c = 2.
Substituting these values into the discriminant formula, we get:
D = (-3)^2 - 4(1)(2)
= 9 - 8
= 1
Since the discriminant is positive (D > 0), the equation has two distinct real solutions.
Therefore, the correct answer is option (b) 2.
**Explanation:**
The discriminant of a quadratic equation determines the number and nature of its solutions.
1. If the discriminant is positive (D > 0), the equation has two distinct real solutions.
2. If the discriminant is zero (D = 0), the equation has one real solution (also called a double root).
3. If the discriminant is negative (D < 0),="" the="" equation="" has="" no="" real="" solutions,="" but="" it="" may="" have="" complex="" />
In this case, the discriminant is positive (D = 1), so the equation x^2 - 3x + 2 = 0 has two distinct real solutions.
To find the values of x, we can use the quadratic formula:
x = (-b ± √D) / 2a
Substituting the values of a, b, and D into the formula, we get:
x = (-(-3) ± √1) / (2(1))
= (3 ± 1) / 2
Therefore, the two solutions are:
x1 = (3 + 1) / 2 = 4 / 2 = 2
x2 = (3 - 1) / 2 = 2 / 2 = 1
Hence, the equation x^2 - 3x + 2 = 0 has two real solutions: x = 1 and x = 2.
Therefore, the correct answer is option (b) 2.
If 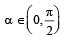 then
then 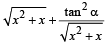 is always greater than or equal to (2003S)
is always greater than or equal to (2003S)- a)2 tanα
- b)1
- c)2
- d)sec2α
Correct answer is option 'A'. Can you explain this answer?
If 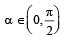 then
then 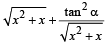 is always greater than or equal to (2003S)
is always greater than or equal to (2003S)
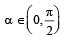 then
then 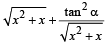 is always greater than or equal to (2003S)
is always greater than or equal to (2003S)a)
2 tanα
b)
1
c)
2
d)
sec2α
|
|
Gaurav Kumar answered |
Let 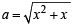 and
and 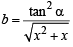
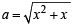 and
and 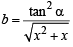
then using AM GM, we get 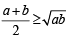
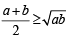
⇒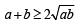
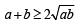
⇒

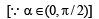
If (x2 + px + 1) is a factor of (ax3 + bx + c), then (1980)- a)a2 + c2 = – ab
- b)a2 – c2 = – ab
- c)a2 – c2 = ab
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If (x2 + px + 1) is a factor of (ax3 + bx + c), then (1980)
a)
a2 + c2 = – ab
b)
a2 – c2 = – ab
c)
a2 – c2 = ab
d)
none of these
|
|
Mira Shah answered |
As (x2 + px + 1) is a factor of ax3 + bx + c, we can assume that zeros of x2 + px + 1 are a, b and that of ax3 + bx + c be α, β, γ so that
α + β = – p .... (i)
αβ = 1 .... (ii)
and α + β + γ = 0 .... (iii)
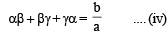

Solving (ii) and (v) we get γ = – c / a.
Also from (i) and (iii) we get γ = p
Also from (i) and (iii) we get γ = p
∴ p = g = – c / a Using equations (i) , (ii) and (iv) we get

 (using γ = p = – c / a)
(using γ = p = – c / a)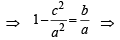 a2 – c2= ab
a2 – c2= ab∴ (c) is the correct answer.
The quadratic equation p(x) = 0 with real coefficients has purely imaginary roots. Then the equation p(p(x)) = 0 has (JEE Adv. 2014)- a)one purely imaginary root
- b)all real roots
- c)two real and two purely imaginary roots
- d)neither real nor purely imaginary roots
Correct answer is option 'D'. Can you explain this answer?
The quadratic equation p(x) = 0 with real coefficients has purely imaginary roots. Then the equation p(p(x)) = 0 has (JEE Adv. 2014)
a)
one purely imaginary root
b)
all real roots
c)
two real and two purely imaginary roots
d)
neither real nor purely imaginary roots
|
|
Avantika Basak answered |
Quadratic equation with real coefficients and purely imaginary roots can be considered as
p(x) = x2 + a = 0 where a > 0 and a ∈R
The p[ p(x)] = 0 ⇒ (x2 + a)2 + a = 0
⇒ x4 + 2ax2 + (a2 + a) = 0
The p[ p(x)] = 0 ⇒ (x2 + a)2 + a = 0
⇒ x4 + 2ax2 + (a2 + a) = 0
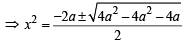
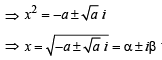 where a, b≠0
where a, b≠0∴ p[p(x)] = 0 has complex roots which are neither purely real nor purely imaginary.
If (1- p) is a root of quadratic equation x2 + px + (1 -p)=0 th en its r oot are [2004]- a)–1, 2
- b)–1, 1
- c)0, –1
- d)0, 1
Correct answer is option 'C'. Can you explain this answer?
If (1- p) is a root of quadratic equation x2 + px + (1 -p)=0 th en its r oot are [2004]
a)
–1, 2
b)
–1, 1
c)
0, –1
d)
0, 1
|
|
Rahul Kumar answered |
If (1 - p) is the root of the given quadratic equation then they are sure satisfied this:-
(1 - p)^2 + p(1- p) + (1- p) = 0
so,
1 - 2p + p^2 + p - p^2 + 1 - p = 0
or,
-2p + 2 = 0
therefore,
p = 2/2 = 1
first root = 1 - p = 1 - 1 = 0
Now quadratic equation is:-
x^2 + x = 0
x(x + 1) = 0
so,
x = 0 and x + 1 = 0
or, x = 0 and -1
Thus we can say that the option (c) is correct
(1 - p)^2 + p(1- p) + (1- p) = 0
so,
1 - 2p + p^2 + p - p^2 + 1 - p = 0
or,
-2p + 2 = 0
therefore,
p = 2/2 = 1
first root = 1 - p = 1 - 1 = 0
Now quadratic equation is:-
x^2 + x = 0
x(x + 1) = 0
so,
x = 0 and x + 1 = 0
or, x = 0 and -1
Thus we can say that the option (c) is correct
If the roots of the equation bx2 + cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is : [2009]- a)less than 4ab
- b)greater than – 4ab
- c)1ess than – 4ab
- d)greater than 4ab
Correct answer is option 'B'. Can you explain this answer?
If the roots of the equation bx2 + cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is : [2009]
a)
less than 4ab
b)
greater than – 4ab
c)
1ess than – 4ab
d)
greater than 4ab
|
|
Deepika Sen answered |
Given that roots of the equation bx2 + cx + a = 0 are imaginary
∴ c2 – 4ab < 0 ....(i)
∴ c2 – 4ab < 0 ....(i)
Let y = 3b2x2 + 6 bc x + 2c2
⇒ 3b2x2 + 6 bc x + 2c2 – y = 0
As x is real, D ≥ 0
⇒ 36 b2c2 – 12 b2 (2c2 – y ) ≥ 0
⇒ 12 b2 (3 c2 – 2 c2+ y ) ≥ 0
⇒ c2 + y ≥ 0
⇒ y ≥ – c2
But from eqn.
(i), c2 < 4ab or – c2 > – 4ab
∴ we get y ≥ – c2 > – 4ab
⇒ y > – 4 ab
⇒ 3b2x2 + 6 bc x + 2c2 – y = 0
As x is real, D ≥ 0
⇒ 36 b2c2 – 12 b2 (2c2 – y ) ≥ 0
⇒ 12 b2 (3 c2 – 2 c2+ y ) ≥ 0
⇒ c2 + y ≥ 0
⇒ y ≥ – c2
But from eqn.
(i), c2 < 4ab or – c2 > – 4ab
∴ we get y ≥ – c2 > – 4ab
⇒ y > – 4 ab
If p and q are the roots of the equation x2+px+q=0, then- a)p = 1, q = –2
- b)p=0, q=1 [2002]
- c)p = –2, q = 0
- d)p = – 2, q=1
Correct answer is option 'A'. Can you explain this answer?
If p and q are the roots of the equation x2+px+q=0, then
a)
p = 1, q = –2
b)
p=0, q=1 [2002]
c)
p = –2, q = 0
d)
p = – 2, q=1
|
|
Ram Mohith answered |
co-efficient of x = - (sum of the roots)
constant term = product of the roots
So, here we get
p + q = -p ----- (1)
pq = q ----- (2)
On solving the above two equations we get p = 1and q = -2
If the sum of the roots of the quadratic equation 2ax2 + bx +c= 0 is equal to the sum of the squares of their reciprocals, then 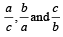 are in [2003]
are in [2003]- a) Arithmetic - Geometric Progression
- b) Arithmetic Progression
- c) Geometric Progression
- d) Harmonic Progression.
Correct answer is option 'D'. Can you explain this answer?
If the sum of the roots of the quadratic equation 2ax2 + bx +c= 0 is equal to the sum of the squares of their reciprocals, then 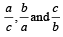 are in [2003]
are in [2003]
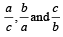 are in [2003]
are in [2003]a)
Arithmetic - Geometric Progression
b)
Arithmetic Progression
c)
Geometric Progression
d)
Harmonic Progression.
|
|
Harsh Singhal answered |
As x+y=1/x^2+1/y^2
on solving we get (b^2-4ac)*2a=-bc^2
on divide by ABC we get our result
on solving we get (b^2-4ac)*2a=-bc^2
on divide by ABC we get our result
Let p,q ∈ {1,2, 3,4} . The number of equations of the form px2 + qx + 1 = 0 having real roots is (1994)- a)15
- b)9
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Let p,q ∈ {1,2, 3,4} . The number of equations of the form px2 + qx + 1 = 0 having real roots is (1994)
a)
15
b)
9
c)
7
d)
8
|
|
Manoj Patel answered |
For the equation px2 + qx + 1 = 0 to have real roots
D ≥ 0 ⇒ q2 ≥ 4p
If p = 1 then q 2 ≥ 4 ⇒ q = 2, 3, 4
If p = 2 then q 2 ≥ 8 ⇒ q = 3, 4
If p = 3 then q2 ≥ 12 ⇒ q =4
If p = 4 then q2 ≥ 16 ⇒ q = 4
∴ No. of req. equations = 7.
For real x, the function 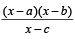 will assume all realvalues provided (1984 - 3 Marks)
will assume all realvalues provided (1984 - 3 Marks)- a)a > b > c
- b)a < b < c
- c)a > c > b
- d)a < c < b
Correct answer is option 'C,D'. Can you explain this answer?
For real x, the function 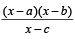 will assume all realvalues provided (1984 - 3 Marks)
will assume all realvalues provided (1984 - 3 Marks)
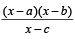 will assume all realvalues provided (1984 - 3 Marks)
will assume all realvalues provided (1984 - 3 Marks)a)
a > b > c
b)
a < b < c
c)
a > c > b
d)
a < c < b

|
Jaideep Sengupta answered |
Let 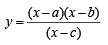
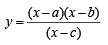
⇒ (x - c) y = x2 - (a + b)x+ ab
⇒ x2 - (a +b + y) x +ab +cy=0
Here, Δ = (a + b + y)2 - 4(ab+ cy)
= y2 + 2 y(a +b - 2c) + (a-b)2
Since x is real and y assumes all real values.
∴ Δ≥ 0 for all real values of y
⇒ y2 + 2 y(a + b - 2c) + (a -b)2≥0
Now we know that the sign of a quad is same as of coeff of y2 provided its descriminant B2 – 4AC < 0
This will be so if, 4(a +b - 2c)2 - 4(a -b)2< 0
or 4 (a +b - 2c+ a - b)(a +b - 2c- a +b) <0
⇒ 16 (a – c) (b – c) < 0
⇒ 16 (c – a) (c – b) < 0 ....(1)
Now,
If a < b then from inequation (1), we get c ∈ (a, b)
⇒ a < c < b
or If a > b then from inequation (1) we get, c ∈ (b,a)
⇒ b < c < a or a > c > b
Thus, we observe that both (c) and (d) are the correct answer.
Chapter doubts & questions for Quadratic Equation and Inequations (Inequalities) - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadratic Equation and Inequations (Inequalities) - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

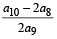 is (2011)
is (2011)
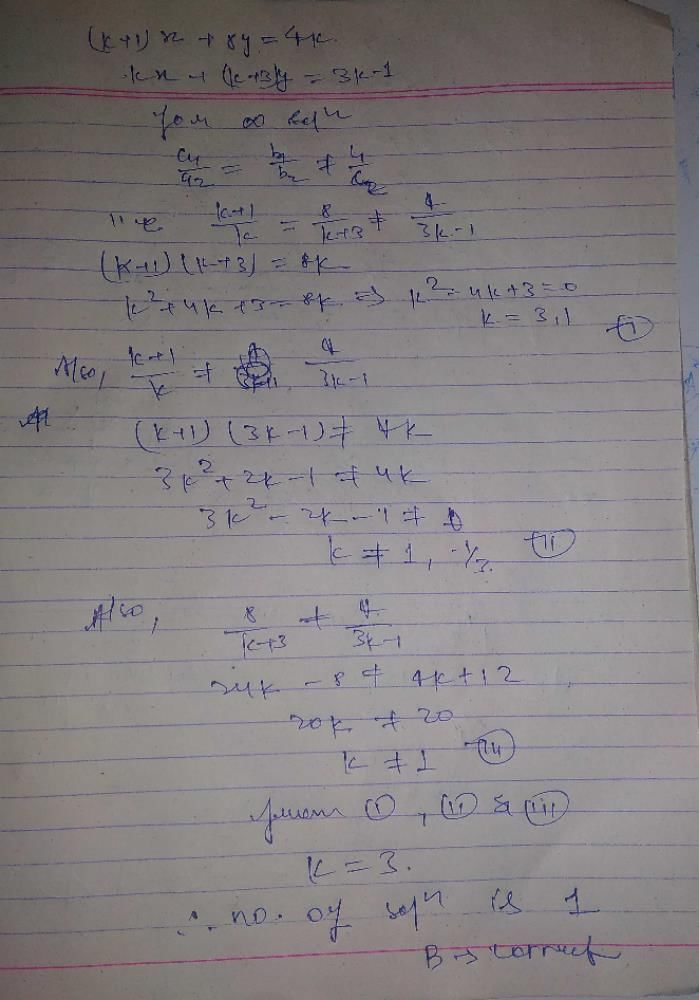
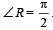 . If tan
. If tan 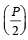 and – tan
and – tan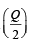 are the roots of ax2 + bx + c = 0, a ≠ 0 then [2005]
are the roots of ax2 + bx + c = 0, a ≠ 0 then [2005]
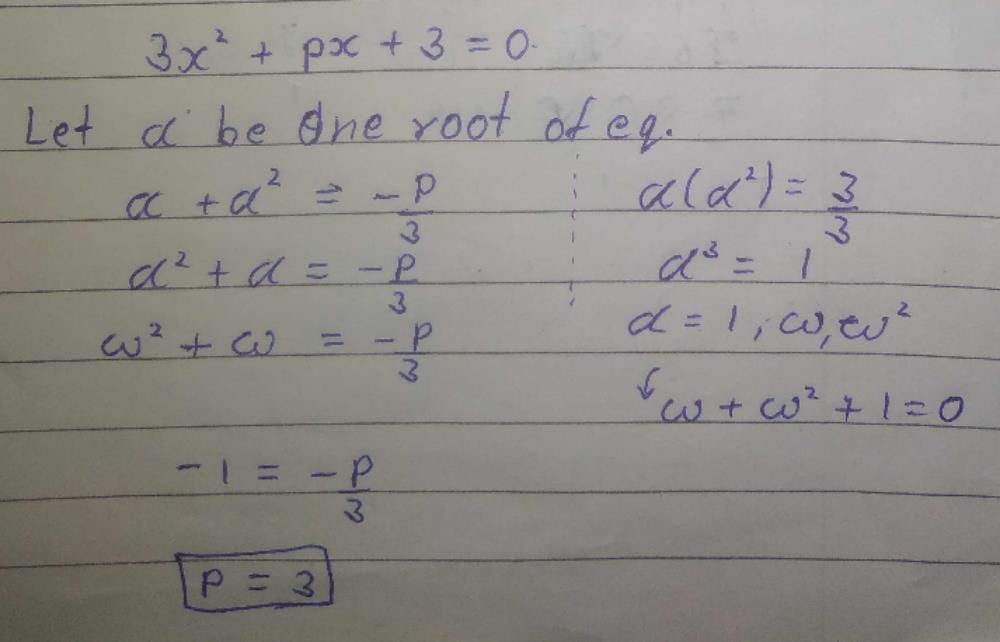
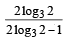
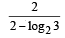
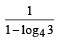
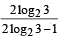
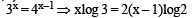
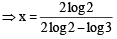



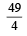


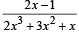 is positive,then S contains (1986 - 2 Marks)
is positive,then S contains (1986 - 2 Marks)