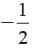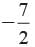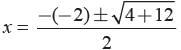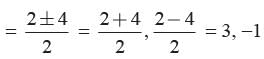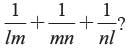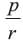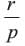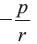All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Polynomials for Class 10 Exam
If the sum of squares of zeros of the quadratic polynomial P(x) = x2 - 8x + k is 40. What is the value of k?- a)12
- b)16
- c)18
- d)8
Correct answer is option 'A'. Can you explain this answer?
If the sum of squares of zeros of the quadratic polynomial P(x) = x2 - 8x + k is 40. What is the value of k?
a)
12
b)
16
c)
18
d)
8
|
Ritu Saxena answered |
P(x) = x2 - 8x + k
If α, and β are its zeros
then α + β = 8, αβ = k
and α2 + β2 = 40
⇒ (α + β)2 - 2αβ = 82 - 2k
⇒ 40 = 64 - 2k
⇒ 2k = 24
⇒ k = 12
If α, and β are its zeros
then α + β = 8, αβ = k
and α2 + β2 = 40
⇒ (α + β)2 - 2αβ = 82 - 2k
⇒ 40 = 64 - 2k
⇒ 2k = 24
⇒ k = 12
If a and b are the zeros of ax2 + bx + c, find the value of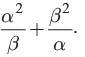 
- a)
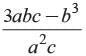
- b)
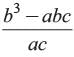
- c)
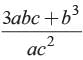
- d)
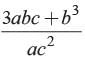
Correct answer is option 'A'. Can you explain this answer?
If a and b are the zeros of ax2 + bx + c, find the value of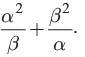
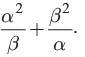
a)
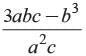
b)
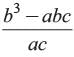
c)
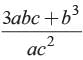
d)
|
|
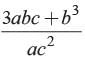
Ritu Saxena answered |
Given a and b are the zeros of ax2 + bx+ c
∴
∴
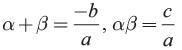
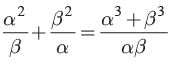
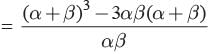
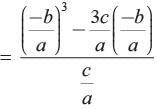
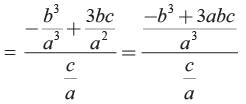
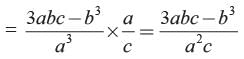
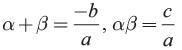
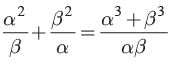
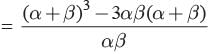
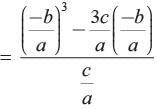
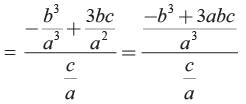
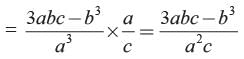
What must be added to f (x) = 4 x 4 +2x3− 2 x 2 +x−1 so that the resulting polynomial is divisible by g (x) = x 2 + 2x −3 ?- a)61x - 65
- b)-61x + 65
- c)-61x - 65
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
What must be added to f (x) = 4 x 4 +2x3− 2 x 2 +x−1 so that the resulting polynomial is divisible by g (x) = x 2 + 2x −3 ?
a)
61x - 65
b)
-61x + 65
c)
-61x - 65
d)
None of these
|
Anmol tiwari answered |
Explanation:
Step 1: Find the quotient when f(x) is divided by g(x)
- To find the quotient, divide f(x) by g(x) using polynomial division.
- Quotient = 4x^2 - 6x + 9
Step 2: Multiply the quotient by g(x) to get the product polynomial
- Multiply the quotient (4x^2 - 6x + 9) by g(x) (x^2 + 2x - 3) to get the product polynomial.
- Product polynomial = 4x^4 - 6x^3 + 9x^2 + 8x^3 - 12x^2 + 18x - 12x^2 + 18x - 27
- Product polynomial = 4x^4 + 2x^3 - 2x^2 + 27
Step 3: Find the difference between the product polynomial and f(x)
- Subtract f(x) from the product polynomial to find the difference.
- Difference = 4x^4 + 2x^3 - 2x^2 + 27 - (4x^4 + 2x^3 - 2x^2 + x - 1)
- Difference = 4x^4 + 2x^3 - 2x^2 + 27 - 4x^4 - 2x^3 + 2x^2 - x + 1
- Difference = -x + 28
Step 4: Determine the polynomial to add to f(x) to make it divisible by g(x)
- The polynomial that needs to be added to f(x) is the difference (-x + 28).
- This can be simplified to -x + 28 = -1x + 28 = -x + 28
Therefore, the polynomial that must be added to f(x) = 4x^4 + 2x^3 - 2x^2 + x - 1 is -x + 28 to make the resulting polynomial divisible by g(x) = x^2 + 2x - 3.
Thus, the correct answer is option -61x + 65.
Step 1: Find the quotient when f(x) is divided by g(x)
- To find the quotient, divide f(x) by g(x) using polynomial division.
- Quotient = 4x^2 - 6x + 9
Step 2: Multiply the quotient by g(x) to get the product polynomial
- Multiply the quotient (4x^2 - 6x + 9) by g(x) (x^2 + 2x - 3) to get the product polynomial.
- Product polynomial = 4x^4 - 6x^3 + 9x^2 + 8x^3 - 12x^2 + 18x - 12x^2 + 18x - 27
- Product polynomial = 4x^4 + 2x^3 - 2x^2 + 27
Step 3: Find the difference between the product polynomial and f(x)
- Subtract f(x) from the product polynomial to find the difference.
- Difference = 4x^4 + 2x^3 - 2x^2 + 27 - (4x^4 + 2x^3 - 2x^2 + x - 1)
- Difference = 4x^4 + 2x^3 - 2x^2 + 27 - 4x^4 - 2x^3 + 2x^2 - x + 1
- Difference = -x + 28
Step 4: Determine the polynomial to add to f(x) to make it divisible by g(x)
- The polynomial that needs to be added to f(x) is the difference (-x + 28).
- This can be simplified to -x + 28 = -1x + 28 = -x + 28
Therefore, the polynomial that must be added to f(x) = 4x^4 + 2x^3 - 2x^2 + x - 1 is -x + 28 to make the resulting polynomial divisible by g(x) = x^2 + 2x - 3.
Thus, the correct answer is option -61x + 65.
If a , b are zeros of 2x2 +5x−10 then what is the value of αβ?- a)-5
- b)5
- c)
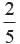
- d)
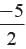
Correct answer is option 'A'. Can you explain this answer?
If a , b are zeros of 2x2 +5x−10 then what is the value of αβ?
a)
-5
b)
5
c)
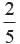
d)
|
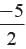
Devansh Chaudhary answered |
There seems to be a typo in the question, as 2x2 5x is not a valid polynomial expression. Please provide the correct expression so that we can help you solve the problem.
Find a cubic polynomial whose roots are -2, -3, and -1.- a)x3 − 6x2+9 x + 6
- b)x3 + 6x2+11x +6
- c)x3 + 6x2−11x −6
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Find a cubic polynomial whose roots are -2, -3, and -1.
a)
x3 − 6x2+9 x + 6
b)
x3 + 6x2+11x +6
c)
x3 + 6x2−11x −6
d)
None of these
|
|
Ritu Saxena answered |
We have α + β+ y = -2 - 3 - 1 = -6 αβ + βy + yα
= (-2) (-3) + (-3) (-1) +(-1) (-2) = 6 + 3 + 2 = 11
and αβγ = (-2) (-3) (-1) = -6
∴ Required polynomial
= x3 - (-6)x2 + 11x - (-6)
= x3 + 6x2 + 11x + 6
= (-2) (-3) + (-3) (-1) +(-1) (-2) = 6 + 3 + 2 = 11
and αβγ = (-2) (-3) (-1) = -6
∴ Required polynomial
= x3 - (-6)x2 + 11x - (-6)
= x3 + 6x2 + 11x + 6
If the polynomial 6x4 + 8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2 + 4x + 1, the remainder comes out to be ax + b. What is the value of a and b?- a)a = 1, b = 2
- b)a = 2, b = 1
- c)a = -2, b = 1
- d)a = -1, b = -2
Correct answer is option 'A'. Can you explain this answer?
If the polynomial 6x4 + 8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2 + 4x + 1, the remainder comes out to be ax + b. What is the value of a and b?
a)
a = 1, b = 2
b)
a = 2, b = 1
c)
a = -2, b = 1
d)
a = -1, b = -2
|
|
Ritu Saxena answered |
3x2 + 4 x +1) 6 x4 + 8 x3 +17 x2 + 21x + 7 (2 x2 + 5
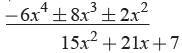
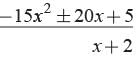
remainder = x + 2
ax + b = x + 2 (Given)
⇒ a = 1; b = 2
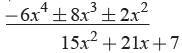
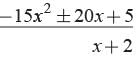
remainder = x + 2
ax + b = x + 2 (Given)
⇒ a = 1; b = 2
For x2 + 2x + 5 to be a factor of x4 + αx2 + β, the values of α and β should respectively be _______.- a)2, 5
- b)5, 25
- c)6, 25
- d)5, 2
Correct answer is option 'C'. Can you explain this answer?
For x2 + 2x + 5 to be a factor of x4 + αx2 + β, the values of α and β should respectively be _______.
a)
2, 5
b)
5, 25
c)
6, 25
d)
5, 2
|
Priya shah answered |
To determine if x^2 + 2x + 5 is a factor of x^4 + ax^3 + bx^2 + cx + d, we need to perform polynomial division.
The division would look like this:
_____________________
x^2 + 2x + 5 | x^4 + ax^3 + bx^2 + cx + d
We start by dividing the first term of the dividend (x^4) by the first term of the divisor (x^2), which gives us x^2. We then multiply x^2 by the divisor (x^2 + 2x + 5), which gives us x^4 + 2x^3 + 5x^2.
Next, we subtract this product from the dividend:
x^4 + ax^3 + bx^2 + cx + d - (x^4 + 2x^3 + 5x^2)
This simplifies to:
ax^3 + (b - 2)x^2 + cx + d - 5x^2
We repeat the process by dividing the first term of the remaining expression (ax^3) by the first term of the divisor (x^2), which gives us a/x. We then multiply a/x by the divisor (x^2 + 2x + 5), which gives us a + 2ax + 5(a/x).
Next, we subtract this product from the remaining expression:
ax^3 + (b - 2)x^2 + cx + d - (a + 2ax + 5(a/x))
This simplifies to:
(b - 2 - 2a)x^2 + (c - 5(a/x))x + (d - 5a)
We repeat this process until we reach the end of the dividend.
For x^2 + 2x + 5 to be a factor, the remainder at the end of the division should be zero. In other words, we need the expression (b - 2 - 2a)x^2 + (c - 5(a/x))x + (d - 5a) to be equal to zero.
Therefore, for x^2 + 2x + 5 to be a factor of x^4 + ax^3 + bx^2 + cx + d, the coefficients (b - 2 - 2a), (c - 5(a/x)), and (d - 5a) must all equal zero.
The division would look like this:
_____________________
x^2 + 2x + 5 | x^4 + ax^3 + bx^2 + cx + d
We start by dividing the first term of the dividend (x^4) by the first term of the divisor (x^2), which gives us x^2. We then multiply x^2 by the divisor (x^2 + 2x + 5), which gives us x^4 + 2x^3 + 5x^2.
Next, we subtract this product from the dividend:
x^4 + ax^3 + bx^2 + cx + d - (x^4 + 2x^3 + 5x^2)
This simplifies to:
ax^3 + (b - 2)x^2 + cx + d - 5x^2
We repeat the process by dividing the first term of the remaining expression (ax^3) by the first term of the divisor (x^2), which gives us a/x. We then multiply a/x by the divisor (x^2 + 2x + 5), which gives us a + 2ax + 5(a/x).
Next, we subtract this product from the remaining expression:
ax^3 + (b - 2)x^2 + cx + d - (a + 2ax + 5(a/x))
This simplifies to:
(b - 2 - 2a)x^2 + (c - 5(a/x))x + (d - 5a)
We repeat this process until we reach the end of the dividend.
For x^2 + 2x + 5 to be a factor, the remainder at the end of the division should be zero. In other words, we need the expression (b - 2 - 2a)x^2 + (c - 5(a/x))x + (d - 5a) to be equal to zero.
Therefore, for x^2 + 2x + 5 to be a factor of x^4 + ax^3 + bx^2 + cx + d, the coefficients (b - 2 - 2a), (c - 5(a/x)), and (d - 5a) must all equal zero.
If one zero of the polynomial f (x) = (k2 + 4) x2 + 13x + 4k is reciprocal of the other, then k is equal to _______.- a)2
- b)–2
- c)1
- d)–1
Correct answer is option 'A'. Can you explain this answer?
If one zero of the polynomial f (x) = (k2 + 4) x2 + 13x + 4k is reciprocal of the other, then k is equal to _______.
a)
2
b)
–2
c)
1
d)
–1
|
|
Anirban Yadav answered |
Understanding the problem:
One zero of the polynomial f(x) = (k^2 + 4)x^2 + 13x + 4k is the reciprocal of the other zero. We need to find the value of k that satisfies this condition.
Key Concept:
If α and β are the zeros of a quadratic polynomial ax^2 + bx + c, then αβ = c/a and α + β = -b/a.
Solution:
Let the zeros of the polynomial f(x) be α and 1/α where α ≠ 0.
Using the sum of zeros formula:
α + 1/α = -13/(k^2 + 4) ...(1)
Using the product of zeros formula:
α * (1/α) = 4k/(k^2 + 4) = 1
4k = k^2 + 4
k^2 - 4k + 4 = 0
(k - 2)^2 = 0
k = 2
Therefore, k = 2 satisfies the condition that one zero of the polynomial is the reciprocal of the other.
Therefore, the correct answer is option 'A' (2).
One zero of the polynomial f(x) = (k^2 + 4)x^2 + 13x + 4k is the reciprocal of the other zero. We need to find the value of k that satisfies this condition.
Key Concept:
If α and β are the zeros of a quadratic polynomial ax^2 + bx + c, then αβ = c/a and α + β = -b/a.
Solution:
Let the zeros of the polynomial f(x) be α and 1/α where α ≠ 0.
Using the sum of zeros formula:
α + 1/α = -13/(k^2 + 4) ...(1)
Using the product of zeros formula:
α * (1/α) = 4k/(k^2 + 4) = 1
4k = k^2 + 4
k^2 - 4k + 4 = 0
(k - 2)^2 = 0
k = 2
Therefore, k = 2 satisfies the condition that one zero of the polynomial is the reciprocal of the other.
Therefore, the correct answer is option 'A' (2).
Area of a triangular field is (x4 – 6x3 – 26x2 + 138x – 35) m2 and base of the triangular field is (x2 – 4x + 1) m. Find the height of the triangular field.- a)2(x2 – 2x – 35) m
- b)1/2(x2 − 2x−35) m
- c)2(3x2 – x – 4) m
- d)1/2(3x2 −x−4) m
Correct answer is option 'A'. Can you explain this answer?
Area of a triangular field is (x4 – 6x3 – 26x2 + 138x – 35) m2 and base of the triangular field is (x2 – 4x + 1) m. Find the height of the triangular field.
a)
2(x2 – 2x – 35) m
b)
1/2(x2 − 2x−35) m
c)
2(3x2 – x – 4) m
d)
1/2(3x2 −x−4) m
|
|
Ritu Saxena answered |
Base of the triangular field = (x2 – 4x + 1) m
Area of the triangular field = (1/2) x Base x Height
Now, x4 – 6x3 – 26x2 + 138x – 35 = 1/2 x (x2 − 4x + 1) × Height
⇒ Height =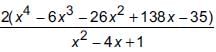
∴ Height = 2(x2 – 2x – 35) m
Area of the triangular field = (1/2) x Base x Height
Now, x4 – 6x3 – 26x2 + 138x – 35 = 1/2 x (x2 − 4x + 1) × Height
⇒ Height =
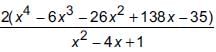
∴ Height = 2(x2 – 2x – 35) m
Two different container contains (2x3 + 2x2 + 3x + 3) L and (4x3 – 2x2 + 6x – 3)L water. What is biggest measure that can measure both quantities exactly?- a)(x2 + 2x) L
- b)(2x2 + 3) L
- c)(2x – 1) L
- d)(x + 1) L
Correct answer is option 'B'. Can you explain this answer?
Two different container contains (2x3 + 2x2 + 3x + 3) L and (4x3 – 2x2 + 6x – 3)L water. What is biggest measure that can measure both quantities exactly?
a)
(x2 + 2x) L
b)
(2x2 + 3) L
c)
(2x – 1) L
d)
(x + 1) L
|
Vivek Bansal answered |
Capacity of both the containers is (2x3 + 2x2 + 3x + 3) L and (4x3 – 2x2 + 6x – 3) L
i.e., (2x2 + 3)(x + 1) L and (2x2 + 3)(2x – 1) L
Required measure is the H.C.F. of capacity of both the containers i.e., (2x2 + 3) L
i.e., (2x2 + 3)(x + 1) L and (2x2 + 3)(2x – 1) L
Required measure is the H.C.F. of capacity of both the containers i.e., (2x2 + 3) L
Which quadratic polynomial has sum of whose zeros is -5 and product of its zero is -12?
- a)x 2 + 5x − 12
- b)x2 - 5x + 12
- c)x2 − 5x + 6
- d)x2 −10x + 12
Correct answer is option 'A'. Can you explain this answer?
Which quadratic polynomial has sum of whose zeros is -5 and product of its zero is -12?
a)
x 2 + 5x − 12
b)
x2 - 5x + 12
c)
x2 − 5x + 6
d)
x2 −10x + 12
|
Malini sharma answered |
Sum and Product of Zeros
- The sum of the zeros of a quadratic polynomial is given by the formula:
- Sum of zeros = -b/a
- The product of the zeros of a quadratic polynomial is given by the formula:
- Product of zeros = c/a
Given Information
- Sum of zeros = -5
- Product of zeros = -12
Solving for the Quadratic Polynomial
- Let the quadratic polynomial be ax^2 + bx + c
- Using the given information, we have:
- -b/a = -5
- c/a = -12
Equations to Solve
1. -b/a = -5
2. c/a = -12
Solving the Equations
- From equation 1, we get: b = 5a
- Substituting b = 5a into equation 2, we get: c/a = -12
- Solving for c, we get: c = -12a
Forming the Quadratic Polynomial
- The quadratic polynomial becomes: ax^2 + 5ax - 12a
Final Quadratic Polynomial
- Factoring out an 'a', we get: a(x^2 + 5x - 12)
- Therefore, the quadratic polynomial is: x^2 + 5x - 12, which corresponds to option 'A'.
- The sum of the zeros of a quadratic polynomial is given by the formula:
- Sum of zeros = -b/a
- The product of the zeros of a quadratic polynomial is given by the formula:
- Product of zeros = c/a
Given Information
- Sum of zeros = -5
- Product of zeros = -12
Solving for the Quadratic Polynomial
- Let the quadratic polynomial be ax^2 + bx + c
- Using the given information, we have:
- -b/a = -5
- c/a = -12
Equations to Solve
1. -b/a = -5
2. c/a = -12
Solving the Equations
- From equation 1, we get: b = 5a
- Substituting b = 5a into equation 2, we get: c/a = -12
- Solving for c, we get: c = -12a
Forming the Quadratic Polynomial
- The quadratic polynomial becomes: ax^2 + 5ax - 12a
Final Quadratic Polynomial
- Factoring out an 'a', we get: a(x^2 + 5x - 12)
- Therefore, the quadratic polynomial is: x^2 + 5x - 12, which corresponds to option 'A'.
What must be subtracted from 8x4 + 14x3 -2x2 + 7x - 8 so that the resulting polynomial is exactly divisible by 4x2 + 3x - 2?- a)4x -10
- b)14x - 10
- c)2x - 10
- d)14x + 10
Correct answer is option 'B'. Can you explain this answer?
What must be subtracted from 8x4 + 14x3 -2x2 + 7x - 8 so that the resulting polynomial is exactly divisible by 4x2 + 3x - 2?
a)
4x -10
b)
14x - 10
c)
2x - 10
d)
14x + 10
|
|
Ritu Saxena answered |
Here 4x2 + 3x - 2) 8x4 + 14x3 - 2x2 + 7x - 8 (2x2 + 2x -1
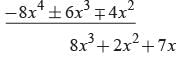
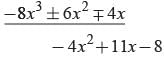
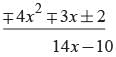
∴ 14x - 10 must be subtracted.
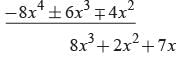
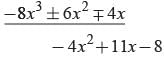
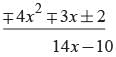
∴ 14x - 10 must be subtracted.
If a and b are the roots of the quadratic equation x2 + px + 12 = 0 with the condition a – b = 1, then the value of ‘p’ is _______.- a)1
- b)7
- c)–7
- d)7 or –7
Correct answer is option 'D'. Can you explain this answer?
If a and b are the roots of the quadratic equation x2 + px + 12 = 0 with the condition a – b = 1, then the value of ‘p’ is _______.
a)
1
b)
7
c)
–7
d)
7 or –7
|
Priyanka Kapoor answered |
Given equation is x2 + px + 12 = 0
Now, if a and b are its roots, then sum of roots, a + b = –p and product of roots, a × b = 12
Also, a – b = 1 (Given)
We know that, (a – b)2 = (a + b)2 – 4ab
⇒ 1 = p2 – 4 × 12 ⇒ 1 = p2 – 48 ⇒ p2 = 49 ⇒ p = ±7
Now, if a and b are its roots, then sum of roots, a + b = –p and product of roots, a × b = 12
Also, a – b = 1 (Given)
We know that, (a – b)2 = (a + b)2 – 4ab
⇒ 1 = p2 – 4 × 12 ⇒ 1 = p2 – 48 ⇒ p2 = 49 ⇒ p = ±7
px3 + qx2 + rx + s = 0 is said to be cubic polynomial, if _______.- a)s ≠ 0
- b)r ≠ 0
- c)q ≠ 0
- d)p ≠ 0
Correct answer is option 'D'. Can you explain this answer?
px3 + qx2 + rx + s = 0 is said to be cubic polynomial, if _______.
a)
s ≠ 0
b)
r ≠ 0
c)
q ≠ 0
d)
p ≠ 0
|
|
Vivek Bansal answered |
For a cubic polynomial to exist, coefficient of term x3 must not be equal to zero.
If α, β are the zeros of a polynomial such α + β = -6 and ab = -4, then what is the polynomial?- a)x2 + 6x−4
- b)x2 − 6x +4
- c)x2 - 6x
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If α, β are the zeros of a polynomial such α + β = -6 and ab = -4, then what is the polynomial?
a)
x2 + 6x−4
b)
x2 − 6x +4
c)
x2 - 6x
d)
None of these
|
Nalini singhania answered |
If what? Please provide more information or context for me to assist you properly.
Raghav had ₹(6x3 + 2x2 + 3x) and he bought (4x2 + 3) shirts. The price of each shirt is ₹(x + 5). How much money is left with Raghav?- a)₹(2x3 – 18x2 – 15)
- b)₹(4x2 + 2x + 3)
- c)₹(x3 – 3x)
- d)₹(2x3 + 2x2 – 15)
Correct answer is option 'A'. Can you explain this answer?
Raghav had ₹(6x3 + 2x2 + 3x) and he bought (4x2 + 3) shirts. The price of each shirt is ₹(x + 5). How much money is left with Raghav?
a)
₹(2x3 – 18x2 – 15)
b)
₹(4x2 + 2x + 3)
c)
₹(x3 – 3x)
d)
₹(2x3 + 2x2 – 15)
|
|
Priyanka Kapoor answered |
Total amount Raghav had = ₹(6x3 + 2x2 + 3x)
Cost of one shirt = ₹(x + 5)
Number of shirts he bought = 4x2 + 3
∴ Amount spent by him = ₹(x + 5)(4x2 + 3)
= ₹(4x3 + 20x2 + 3x + 15)
Hence, money left with Raghav
= ₹(6x3 + 2x2 + 3x – 4x3 – 20x2 – 3x – 15)
= ₹(2x3 – 18x2 – 15)
Cost of one shirt = ₹(x + 5)
Number of shirts he bought = 4x2 + 3
∴ Amount spent by him = ₹(x + 5)(4x2 + 3)
= ₹(4x3 + 20x2 + 3x + 15)
Hence, money left with Raghav
= ₹(6x3 + 2x2 + 3x – 4x3 – 20x2 – 3x – 15)
= ₹(2x3 – 18x2 – 15)
A polynomial of the form ax5 + bx3 + cx2 + dx + e has atmost _______ zeroes.- a)3
- b)5
- c)7
- d)11
Correct answer is option 'B'. Can you explain this answer?
A polynomial of the form ax5 + bx3 + cx2 + dx + e has atmost _______ zeroes.
a)
3
b)
5
c)
7
d)
11
|
|
Madhavi singhania answered |
To find out the maximum number of zeroes a polynomial of the form ax^5 + bx^3 + cx^2 + dx + e can have, we need to consider the degree of the polynomial.
Degree of a polynomial:
The degree of a polynomial is the highest power of the variable (x in this case) in the polynomial.
In this case, the highest power of the variable is 5, so the degree of the polynomial is 5.
Fundamental Theorem of Algebra:
The Fundamental Theorem of Algebra states that a polynomial of degree 'n' has exactly 'n' complex zeroes, counting multiplicities.
Complex zeroes:
Complex zeroes are solutions to the equation of the polynomial in the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit (√-1).
Number of zeroes:
Since the degree of the given polynomial is 5, according to the Fundamental Theorem of Algebra, it can have at most 5 complex zeroes.
Multiplicity:
The multiplicity of a zero refers to the number of times it appears as a solution. It is determined by the exponent of the factor (x - r) in the factored form of the polynomial, where 'r' is the zero.
Example:
If the polynomial has a factor (x - r)^2, then 'r' is a zero of multiplicity 2.
Conclusion:
In this case, the polynomial of the form ax^5 + bx^3 + cx^2 + dx + e can have at most 5 zeroes, according to the Fundamental Theorem of Algebra. Therefore, the correct answer is option 'B' - 5.
Degree of a polynomial:
The degree of a polynomial is the highest power of the variable (x in this case) in the polynomial.
In this case, the highest power of the variable is 5, so the degree of the polynomial is 5.
Fundamental Theorem of Algebra:
The Fundamental Theorem of Algebra states that a polynomial of degree 'n' has exactly 'n' complex zeroes, counting multiplicities.
Complex zeroes:
Complex zeroes are solutions to the equation of the polynomial in the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit (√-1).
Number of zeroes:
Since the degree of the given polynomial is 5, according to the Fundamental Theorem of Algebra, it can have at most 5 complex zeroes.
Multiplicity:
The multiplicity of a zero refers to the number of times it appears as a solution. It is determined by the exponent of the factor (x - r) in the factored form of the polynomial, where 'r' is the zero.
Example:
If the polynomial has a factor (x - r)^2, then 'r' is a zero of multiplicity 2.
Conclusion:
In this case, the polynomial of the form ax^5 + bx^3 + cx^2 + dx + e can have at most 5 zeroes, according to the Fundamental Theorem of Algebra. Therefore, the correct answer is option 'B' - 5.
If α and β are the roots of the equation 2x2 – 7x + 8 = 0, then the equation whose roots are(3α – 4β) and (3β – 4α) is _______.- a)2x2 + 7x + 98 = 0
- b)x2 + 7x + 98 = 0
- c)2x2 – 7x – 98 = 0
- d)2x2 – 7x + 98 = 0
Correct answer is option 'A'. Can you explain this answer?
If α and β are the roots of the equation 2x2 – 7x + 8 = 0, then the equation whose roots are(3α – 4β) and (3β – 4α) is _______.
a)
2x2 + 7x + 98 = 0
b)
x2 + 7x + 98 = 0
c)
2x2 – 7x – 98 = 0
d)
2x2 – 7x + 98 = 0
|
|
Sonam das answered |
You could have any superpower, what would it be and why?
If the sum of the product of the zeroes taken two at a time of the polynomial f(x) = 2x3 – 3x2 + 4tx – 5 is –8, then the value of t is _______.- a)2
- b)4
- c)–2
- d)– 4
Correct answer is option 'D'. Can you explain this answer?
If the sum of the product of the zeroes taken two at a time of the polynomial f(x) = 2x3 – 3x2 + 4tx – 5 is –8, then the value of t is _______.
a)
2
b)
4
c)
–2
d)
– 4
|
|
Sumitra verma answered |
To find the sum of the product of the zeroes taken two at a time, we need to find the product of each pair of zeroes and then sum them up.
Let the zeroes of the polynomial f(x) = 2x^3 + px^2 + qx + r be a, b, and c.
The product of the zeroes taken two at a time can be expressed as:
ab + ac + bc
Using Vieta's formulas, we know that:
a + b + c = -p/2
ab + ac + bc = q/2
abc = -r/2
Now, we need to find the value of q/2.
From the given information, we can see that the coefficient of x term is q, which is the sum of the zeroes taken two at a time. Hence, q/2 is equal to the sum of the product of the zeroes taken two at a time.
Therefore, the sum of the product of the zeroes taken two at a time is q/2.
Let the zeroes of the polynomial f(x) = 2x^3 + px^2 + qx + r be a, b, and c.
The product of the zeroes taken two at a time can be expressed as:
ab + ac + bc
Using Vieta's formulas, we know that:
a + b + c = -p/2
ab + ac + bc = q/2
abc = -r/2
Now, we need to find the value of q/2.
From the given information, we can see that the coefficient of x term is q, which is the sum of the zeroes taken two at a time. Hence, q/2 is equal to the sum of the product of the zeroes taken two at a time.
Therefore, the sum of the product of the zeroes taken two at a time is q/2.
What is the cubic polynomial whose zeros are α, β, γ such that α + β + γ = 4. abg = - 6 and αβ + βγ + γα = 1?- a)x3 − 4x2 + x +6
- b)x3 − 2x2− x +6
- c)x3 − 4x2+4 x − 6
- d)x3 - 4x2- x -6
Correct answer is option 'A'. Can you explain this answer?
What is the cubic polynomial whose zeros are α, β, γ such that α + β + γ = 4. abg = - 6 and αβ + βγ + γα = 1?
a)
x3 − 4x2 + x +6
b)
x3 − 2x2− x +6
c)
x3 − 4x2+4 x − 6
d)
x3 - 4x2- x -6
|
|
Ritu Saxena answered |
Required polynomial
= P(x ) = x3 - (α + β + γ)x2 + (αβ + βγ + γα)x
- αβγ
= x3 − 4x2+ x + 6
= P(x ) = x3 - (α + β + γ)x2 + (αβ + βγ + γα)x
- αβγ
= x3 − 4x2+ x + 6
11. Find a cubic polynomial whose zeros are α, β, g such that α + β + γ= 6, αβ + βγ + gα = -1 and αβγ = -30.- a)x3 − 6x2− x +30
- b)x3 + 6x2+ x −30
- c)x3 −x2− 6 x +30
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
11. Find a cubic polynomial whose zeros are α, β, g such that α + β + γ= 6, αβ + βγ + gα = -1 and αβγ = -30.
a)
x3 − 6x2− x +30
b)
x3 + 6x2+ x −30
c)
x3 −x2− 6 x +30
d)
None of these
|
|
Madhuri bajaj answered |
To find a cubic polynomial with zeros -2, 0, and 3, we can use the fact that if a polynomial has a zero at a certain value, then it must have a factor of (x - zero).
So, for the given zeros, the factors are: (x - (-2)), (x - 0), and (x - 3).
Simplifying these factors, we get: (x + 2), x, and (x - 3).
To find the cubic polynomial, we multiply these factors together:
(x + 2)(x)(x - 3)
Expanding this expression, we get:
(x^2 + 2x)(x - 3)
Now, we multiply each term in the first expression by each term in the second expression:
x^2(x - 3) + 2x(x - 3)
Expanding further, we get:
x^3 - 3x^2 + 2x^2 - 6x
Combining like terms, we have:
x^3 - x^2 - 6x
Therefore, the cubic polynomial with zeros -2, 0, and 3 is:
f(x) = x^3 - x^2 - 6x
So, for the given zeros, the factors are: (x - (-2)), (x - 0), and (x - 3).
Simplifying these factors, we get: (x + 2), x, and (x - 3).
To find the cubic polynomial, we multiply these factors together:
(x + 2)(x)(x - 3)
Expanding this expression, we get:
(x^2 + 2x)(x - 3)
Now, we multiply each term in the first expression by each term in the second expression:
x^2(x - 3) + 2x(x - 3)
Expanding further, we get:
x^3 - 3x^2 + 2x^2 - 6x
Combining like terms, we have:
x^3 - x^2 - 6x
Therefore, the cubic polynomial with zeros -2, 0, and 3 is:
f(x) = x^3 - x^2 - 6x
A cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time and the product of its zeroes as –3, 8, 4 respectively, is _______.- a)x3 – 3x2 – 8x – 4
- b)x3 + 3x2 – 8x – 4
- c)x3 + 3x2 + 8x – 4
- d)x3 – 3x2 – 8x + 4
Correct answer is option 'C'. Can you explain this answer?
A cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time and the product of its zeroes as –3, 8, 4 respectively, is _______.
a)
x3 – 3x2 – 8x – 4
b)
x3 + 3x2 – 8x – 4
c)
x3 + 3x2 + 8x – 4
d)
x3 – 3x2 – 8x + 4
|
Avni dubey answered |
Let the cubic polynomial be $ax^3+bx^2+cx+d$. By Vieta's formulas, we have:
Sum of zeroes = $-\frac{b}{a}$
Sum of product of zeroes taken two at a time = $\frac{c}{a}$
Product of zeroes = $-\frac{d}{a}$
We want the sum of these three quantities, which is:
$-\frac{b}{a}+\frac{c}{a}-\frac{d}{a}=\boxed{\frac{c-b-d}{a}}$
Sum of zeroes = $-\frac{b}{a}$
Sum of product of zeroes taken two at a time = $\frac{c}{a}$
Product of zeroes = $-\frac{d}{a}$
We want the sum of these three quantities, which is:
$-\frac{b}{a}+\frac{c}{a}-\frac{d}{a}=\boxed{\frac{c-b-d}{a}}$
What will be the value of p(3), if 3 is one of zeroes of polynomial p(x) = x3 + bx + D?- a)3
- b)D
- c)27
- d)0
Correct answer is option 'D'. Can you explain this answer?
What will be the value of p(3), if 3 is one of zeroes of polynomial p(x) = x3 + bx + D?
a)
3
b)
D
c)
27
d)
0
|
|
Gauri iyer answered |
To find the value of p(3), we need to substitute 3 into the polynomial p(x) = x^3 + bx + D.
Let's break down the steps to find the value of p(3):
Step 1: Substitute x with 3 in the polynomial equation:
p(3) = (3)^3 + b(3) + D
Step 2: Simplify the equation:
p(3) = 27 + 3b + D
Since we don't have any specific values for b and D, we cannot simplify the equation any further. Therefore, the value of p(3) is 27 + 3b + D.
Now, let's analyze the given options:
a) 3: This option suggests that p(3) equals 3, but based on the equation p(3) = 27 + 3b + D, there is no guarantee that the value will be exactly 3.
b) D: This option suggests that p(3) equals D, which is one of the variables in the equation. While it is possible for p(3) to equal D if b is zero, we cannot determine the value without more information.
c) 27: This option suggests that p(3) equals 27. While this is a possibility, it is not always the case since the equation also contains the variables b and D. Without specific values for b and D, we cannot determine if p(3) equals 27.
d) 0: This option suggests that p(3) equals 0. Based on the equation p(3) = 27 + 3b + D, we can see that if 27 + 3b + D equals 0, then p(3) will indeed be 0. This is the correct answer since it satisfies the equation.
Therefore, the correct answer is option 'd' - 0.
Let's break down the steps to find the value of p(3):
Step 1: Substitute x with 3 in the polynomial equation:
p(3) = (3)^3 + b(3) + D
Step 2: Simplify the equation:
p(3) = 27 + 3b + D
Since we don't have any specific values for b and D, we cannot simplify the equation any further. Therefore, the value of p(3) is 27 + 3b + D.
Now, let's analyze the given options:
a) 3: This option suggests that p(3) equals 3, but based on the equation p(3) = 27 + 3b + D, there is no guarantee that the value will be exactly 3.
b) D: This option suggests that p(3) equals D, which is one of the variables in the equation. While it is possible for p(3) to equal D if b is zero, we cannot determine the value without more information.
c) 27: This option suggests that p(3) equals 27. While this is a possibility, it is not always the case since the equation also contains the variables b and D. Without specific values for b and D, we cannot determine if p(3) equals 27.
d) 0: This option suggests that p(3) equals 0. Based on the equation p(3) = 27 + 3b + D, we can see that if 27 + 3b + D equals 0, then p(3) will indeed be 0. This is the correct answer since it satisfies the equation.
Therefore, the correct answer is option 'd' - 0.
If p, q are the zeroes of the polynomial f(x) = x2 + k(x – 1) – c, then (p – 1)(q – 1) is equal to _______.- a)c –1
- b)1 – c
- c)c
- d)1 + c
Correct answer is option 'B'. Can you explain this answer?
If p, q are the zeroes of the polynomial f(x) = x2 + k(x – 1) – c, then (p – 1)(q – 1) is equal to _______.
a)
c –1
b)
1 – c
c)
c
d)
1 + c
|
Baishali Kulkarni answered |
It seems like the question is incomplete. Could you please provide the complete expression for the polynomial f(x)?
If sum of all zeros of the polynomial 5x2 – (3 + k)x + 7 is zero, then zeroes of the polynomial 2x2 – 2(k + 11)x + 30 are- a)3, 5
- b)7, 9
- c)3, 6
- d)2, 5
Correct answer is option 'A'. Can you explain this answer?
If sum of all zeros of the polynomial 5x2 – (3 + k)x + 7 is zero, then zeroes of the polynomial 2x2 – 2(k + 11)x + 30 are
a)
3, 5
b)
7, 9
c)
3, 6
d)
2, 5
|
|
Vivek Bansal answered |
Sum of zeroes of polynomial
5x2– (3 + k)x + 7 is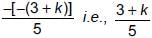
According to question, ((3+k)/5) = 0 ⇒ k = –3
Now, 2x2 – 2(k + 11)x + 30 becomes 2x2 – 16x + 30.
i.e., 2x2 – 16x + 30 = 0 or x2 – 8x + 15 = 0
⇒ x = 3, 5
Hence, zeroes of polynomial 2x2 – 16x + 30 are 3, 5.
5x2– (3 + k)x + 7 is
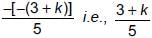
According to question, ((3+k)/5) = 0 ⇒ k = –3
Now, 2x2 – 2(k + 11)x + 30 becomes 2x2 – 16x + 30.
i.e., 2x2 – 16x + 30 = 0 or x2 – 8x + 15 = 0
⇒ x = 3, 5
Hence, zeroes of polynomial 2x2 – 16x + 30 are 3, 5.
A rectangular garden of length (2x3 + 5x2 – 7) m has the perimeter (4x3 – 2x2 + 4) m. Find the breadth of the garden.- a)(6x2 – 9) m
- b)(–6x2 + 9) m
- c)(2x3 – 7x2 + 11) m
- d)(6x3 + 7x2 + 9) m
Correct answer is option 'B'. Can you explain this answer?
A rectangular garden of length (2x3 + 5x2 – 7) m has the perimeter (4x3 – 2x2 + 4) m. Find the breadth of the garden.
a)
(6x2 – 9) m
b)
(–6x2 + 9) m
c)
(2x3 – 7x2 + 11) m
d)
(6x3 + 7x2 + 9) m
|
|
Ritu Saxena answered |
Length of the garden = (2x3 + 5x2 – 7) m
Perimeter of the garden = 2 × (length + breadth)
∴ 4x3 - 2x2 + 4 = 2(2x3 + 5x2 – 7 + breadth)
⇒ 2x3 – x2 + 2 = (2x3 + 5x2 – 7) + breadth
So, breadth of the rectangle
= 2x3 – x2 + 2 – 2x3 – 5x2 + 7 = (–6x2 + 9) m
Perimeter of the garden = 2 × (length + breadth)
∴ 4x3 - 2x2 + 4 = 2(2x3 + 5x2 – 7 + breadth)
⇒ 2x3 – x2 + 2 = (2x3 + 5x2 – 7) + breadth
So, breadth of the rectangle
= 2x3 – x2 + 2 – 2x3 – 5x2 + 7 = (–6x2 + 9) m
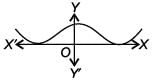
Which of the following graph has more than three distinct real roots?- a)
- b)
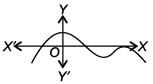
- c)
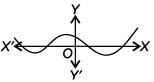
- d)
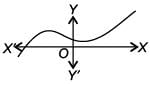
Correct answer is option 'C'. Can you explain this answer?
Which of the following graph has more than three distinct real roots?
a)
b)
c)
d)
|
|
Priyanka Kapoor answered |
For more than three distinct real roots the graph must cut x-axis at least four times. So, graph in option (C) has more than three distinct real roots.
If α , β are the zeros of quadratic polynomial 6x2 + x - 2, find the value of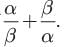 
- a)
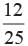
- b)
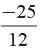
- c)
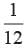
- d)
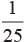
Correct answer is option 'B'. Can you explain this answer?
If α , β are the zeros of quadratic polynomial 6x2 + x - 2, find the value of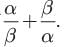
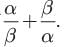
a)
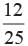
b)
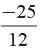
c)
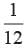
d)
|
|
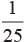
Ritu Saxena answered |
Given 6 x2 +x−2
If a, b are its zeros
then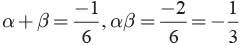
Now
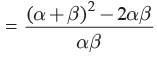
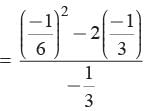
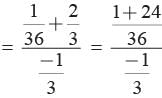
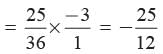
If a, b are its zeros
then
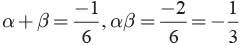
Now
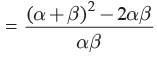
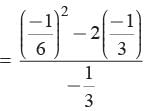
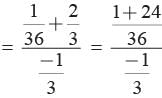
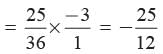
If α , β are zeros of the polynomial x2 −px+d , then what is the value of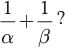 
- a)
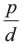
- b)
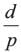
- c)1
- d)
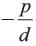
Correct answer is option 'A'. Can you explain this answer?
If α , β are zeros of the polynomial x2 −px+d , then what is the value of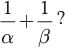
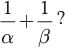
a)
b)
c)
1
d)
|
|
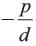
Ritu Saxena answered |
Given α and β are zeros of x2 −px+d
then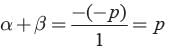
and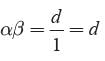
∴
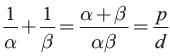
then
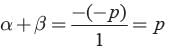
and
∴
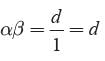
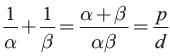
Find the polynomial which when divided by −x2 + x −1 gives a quotient x - 2 and remainder 3.- a)−x3+ 3x2 −3x+ 5
- b)-x3- 3x2 -3x- 5
- c)x3 − 3x2+3x − 5
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the polynomial which when divided by −x2 + x −1 gives a quotient x - 2 and remainder 3.
a)
−x3+ 3x2 −3x+ 5
b)
-x3- 3x2 -3x- 5
c)
x3 − 3x2+3x − 5
d)
None of these
|
|
Ritu Saxena answered |
Polynomial = (−x2+x −1) ( x−2) + 3
= −x3 + 2x2 + x2−2x − x+ 2 +3
= −x3+ 3x2 −3x+ 5
= −x3 + 2x2 + x2−2x − x+ 2 +3
= −x3+ 3x2 −3x+ 5
If divisor is 2 − x + x2 and quotient is (3x - 1) then what is the dividend if dividend is completely divisible?- a)3x3 −2x2− 7 x +2
- b)3x3 −4x2+ 7 x −2
- c)3x3 −4x2− 7 x +2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If divisor is 2 − x + x2 and quotient is (3x - 1) then what is the dividend if dividend is completely divisible?
a)
3x3 −2x2− 7 x +2
b)
3x3 −4x2+ 7 x −2
c)
3x3 −4x2− 7 x +2
d)
None of these
|
|
Ritu Saxena answered |
Here (2 − x+x2)(3x −1)
= 6 x −2− 3x2 + x+3x3 − x2
= 3x3−4x2+ 7x −2
= 6 x −2− 3x2 + x+3x3 − x2
= 3x3−4x2+ 7x −2
Find the other two zeros of the polynomial 2x4 - 3x3 - 3x2 + 6x - 2 if its two roots are √2 and - √2.- a)1 and
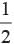
- b)-1 and
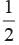
- c)2 and 1
- d)-2 and 1
Correct answer is option 'A'. Can you explain this answer?
Find the other two zeros of the polynomial 2x4 - 3x3 - 3x2 + 6x - 2 if its two roots are √2 and - √2.
a)
1 and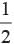
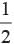
b)
-1 and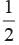
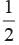
c)
2 and 1
d)
-2 and 1
|
|
Ritu Saxena answered |
2 x4 −3x3− 3x2 +6x− 2
Let the other roots be α and β.
Sum of the roots =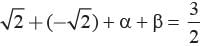
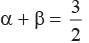…(1)
Product of roots =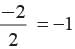
√2 + (- √2)αβ = -1 ⇒ αβ =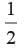
…(2)
(α - β)2 = (α + β)2 - 4αβ
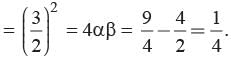
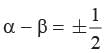…(3)
From equation (1) and (3)
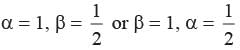
Let the other roots be α and β.
Sum of the roots =
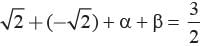
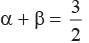…(1)Product of roots =
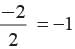
√2 + (- √2)αβ = -1 ⇒ αβ =
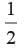…(2)(α - β)2 = (α + β)2 - 4αβ
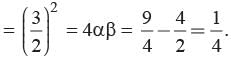
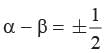…(3)From equation (1) and (3)
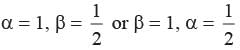
When x3 – 3x2 + 3x + 5 is divided by x2 – x + 1, the quotient and remainder are _______.- a)x + 2, 7
- b)x – 2, –7
- c)x – 2, 7
- d)x + 2, –7
Correct answer is option 'C'. Can you explain this answer?
When x3 – 3x2 + 3x + 5 is divided by x2 – x + 1, the quotient and remainder are _______.
a)
x + 2, 7
b)
x – 2, –7
c)
x – 2, 7
d)
x + 2, –7
|
|
Ritu Saxena answered |
This can be done either by long division as shown in the image
We can see the division gives us a quotient (x − 2) and a remainder 3
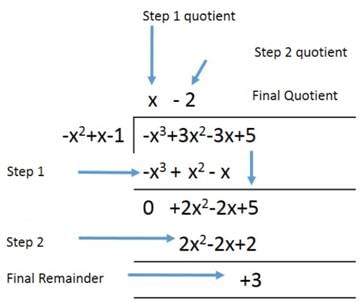
We can see the division gives us a quotient (x − 2) and a remainder 3
If a , b are the zeros of the polynomial x2 - 5x + P such that α - β = 1. What is the value of P?- a)1/6
- b)6
- c)-6
- d)3
Correct answer is option 'B'. Can you explain this answer?
If a , b are the zeros of the polynomial x2 - 5x + P such that α - β = 1. What is the value of P?
a)
1/6
b)
6
c)
-6
d)
3
|
|
Ritu Saxena answered |
Here α, β are the zeros of x2 - 5x + P
then α + β = 5 …(1)
and αβ = P
α - β = 1 …(2)
Solving (1) and (2) we get
2α = 6 ⇒ α = 3
and β = 5 - 3 = 2
∴ αβ = P = (3) (2) = 6
then α + β = 5 …(1)
and αβ = P
α - β = 1 …(2)
Solving (1) and (2) we get
2α = 6 ⇒ α = 3
and β = 5 - 3 = 2
∴ αβ = P = (3) (2) = 6
Length and breadth of a rectangular park are (3x2 + 2x) m and (2x3 – 3) m respectively. Find the area of the park, when x = 3.- a)1924 m2
- b)1492 m2
- c)1881 m2
- d)1683 m2
Correct answer is option 'D'. Can you explain this answer?
Length and breadth of a rectangular park are (3x2 + 2x) m and (2x3 – 3) m respectively. Find the area of the park, when x = 3.
a)
1924 m2
b)
1492 m2
c)
1881 m2
d)
1683 m2
|
|
Vivek Bansal answered |
Length of rectangular park = (3x2 + 2x) m
Breadth of rectangular park = (2x3 – 3) m
Area of park = length × breadth
= (3x2 + 2x) (2x3 – 3) = (6x5 + 4x4 – 9x2 – 6x) m
For x = 3, 6x5 + 4x4 – 9x2 – 6x
= 6 × 243 + 4 × 81 – 9 × 9 – 6 × 3 = 1683
Hence, area of park = 1683 m2
Breadth of rectangular park = (2x3 – 3) m
Area of park = length × breadth
= (3x2 + 2x) (2x3 – 3) = (6x5 + 4x4 – 9x2 – 6x) m
For x = 3, 6x5 + 4x4 – 9x2 – 6x
= 6 × 243 + 4 × 81 – 9 × 9 – 6 × 3 = 1683
Hence, area of park = 1683 m2
What should be subtracted from f (x) = 6x3 + 11x2 – 39x – 65 so that f(x) is exactly divisible by x2 + x – 1?- a)38x + 60
- b)–38x – 60
- c)–19x – 30
- d)9x + 10
Correct answer is option 'B'. Can you explain this answer?
What should be subtracted from f (x) = 6x3 + 11x2 – 39x – 65 so that f(x) is exactly divisible by x2 + x – 1?
a)
38x + 60
b)
–38x – 60
c)
–19x – 30
d)
9x + 10
|
|
Priyanka Kapoor answered |
By long division method, we have
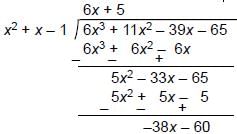
We must subtract the remainder so that f(x) is exactly divisible by x2 + x – 1
Hence, –38x – 60 is to be subtracted.
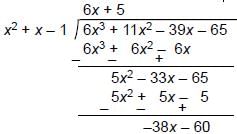
We must subtract the remainder so that f(x) is exactly divisible by x2 + x – 1
Hence, –38x – 60 is to be subtracted.
If the product of two zeros of the polynomial 2 x3 +6x2−4x + 9 is 3 then what is its third zero?- a)3/2
- b)2/3
- c)1/2
- d)
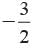
Correct answer is option 'D'. Can you explain this answer?
If the product of two zeros of the polynomial 2 x3 +6x2−4x + 9 is 3 then what is its third zero?
a)
3/2
b)
2/3
c)
1/2
d)
|
|
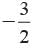
Ritu Saxena answered |
If α and β are two zeros then αβ = 3 Let third root be γ.
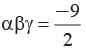
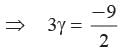
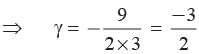
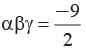
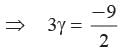
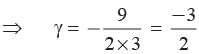
What are the zeros of abx2 + (b2 - ac)x - bc?- a)
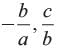
- b)
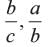
- c)
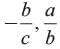
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What are the zeros of abx2 + (b2 - ac)x - bc?
a)
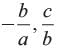
b)
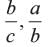
c)
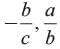
d)
None of these
|
|
Ritu Saxena answered |
We have abx 2 + (b2−ac)x − bc
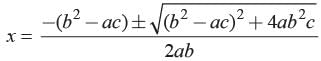
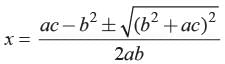
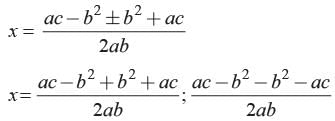
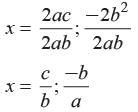
The zeros of the given polynomial are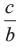
and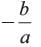 
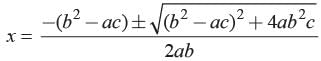
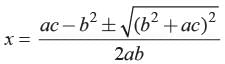
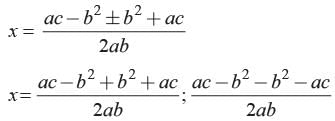
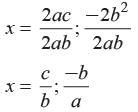
The zeros of the given polynomial are
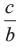and 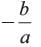If divisor is x -1-x 2 and dividend is 3x 2 −x3−3x + 5, then what is the remainder?- a)x - 3
- b)3
- c)-3
- d)x + 3
Correct answer is option 'B'. Can you explain this answer?
If divisor is x -1-x 2 and dividend is 3x 2 −x3−3x + 5, then what is the remainder?
a)
x - 3
b)
3
c)
-3
d)
x + 3
|
|
Ritu Saxena answered |
-x2 + x - 1) - x3 + 3x2 - 3x + 5( x - 2
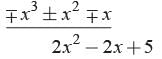
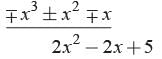
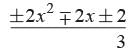
If α, β be two zeroes of the quadratic polynomial ax2 + bx – c = 0, then find the value of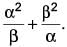 
- a)
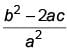
- b)
- c)
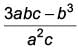
- d)
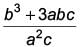
Correct answer is option 'D'. Can you explain this answer?
If α, β be two zeroes of the quadratic polynomial ax2 + bx – c = 0, then find the value of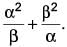
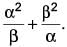
a)
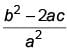
b)
c)
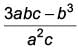
d)
|
|
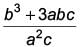
Ritu Saxena answered |
Since, a and b are the zeroes of quadratic equation ax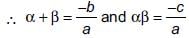
2 + bx – c = 0
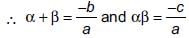
Now,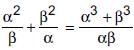
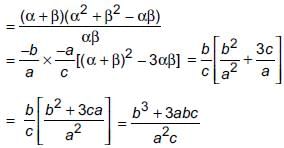
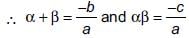2 + bx – c = 0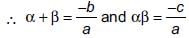Now,
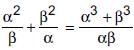
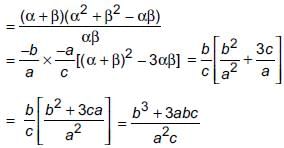
What is the cubic polynomial in which the sum, sum of the products of its zeros taken at a time and product of its zeros as 2, -7, -14 respectively?- a)k (x3 − 2 x2−7x +14)
- b)k (x3 − 2 x2 + 8x −14)
- c)k (x3 + 2 x2−7x − 4)
- d)k (x3 - x2-x -14)
Correct answer is option 'A'. Can you explain this answer?
What is the cubic polynomial in which the sum, sum of the products of its zeros taken at a time and product of its zeros as 2, -7, -14 respectively?
a)
k (x3 − 2 x2−7x +14)
b)
k (x3 − 2 x2 + 8x −14)
c)
k (x3 + 2 x2−7x − 4)
d)
k (x3 - x2-x -14)
|
|
Ritu Saxena answered |
Given a + b+ γ = 2 =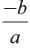 
⇒ b = -2a
αβ + βγ + γα = -7 =
⇒ c = -7a
αβγ = -14 =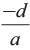
⇒ d = 14a
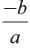⇒ b = -2aαβ + βγ + γα = -7 =
⇒ c = -7aαβγ = -14 =
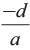⇒ d = 14ab : c : d = -2 : -7 : 14
Cubic polynomial is
k(x3 - 2x2 - 7x + 14)
Cubic polynomial is
k(x3 - 2x2 - 7x + 14)
Chapter doubts & questions for Polynomials - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomials - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Olympiad Preparation for Class 10
70 videos|242 docs|187 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily