All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Quadratic Equations for Class 10 Exam
If 2 is a root of the equation x2 + bx + 12 = 0 and the equation x2 + bx + q = 0 has equal roots, then q is equal to- a)8
- b)– 8
- c)16
- d)–16
Correct answer is option 'C'. Can you explain this answer?
If 2 is a root of the equation x2 + bx + 12 = 0 and the equation x2 + bx + q = 0 has equal roots, then q is equal to
a)
8
b)
– 8
c)
16
d)
–16
|
Sheena mehta answered |
To find the value of q, we can use the fact that if 2 is a root of the equation x^2 + bx + 12 = 0, then (x-2) is a factor of the equation.
So, we can write the equation as (x-2)(x-k) = 0, where k is the other root of the equation.
Expanding this equation, we get x^2 - (2+k)x + 2k = 0.
Since the equation x^2 - bx + q = 0 has equal roots, the discriminant (b^2 - 4ac) must be equal to 0.
In this case, a = 1, b = -(2+k), and c = 2k.
So, we have (-(2+k))^2 - 4(1)(2k) = 0.
Simplifying, we get (2+k)^2 - 8k = 0.
Expanding and rearranging, we get 4 + 4k + k^2 - 8k = 0.
Combining like terms, we get k^2 - 4k + 4 = 0.
This quadratic equation can be factored as (k-2)^2 = 0.
So, the other root of the equation is k = 2.
Therefore, q = 2k = 2(2) = 4.
Therefore, q is equal to 4. Answer: b) 4.
So, we can write the equation as (x-2)(x-k) = 0, where k is the other root of the equation.
Expanding this equation, we get x^2 - (2+k)x + 2k = 0.
Since the equation x^2 - bx + q = 0 has equal roots, the discriminant (b^2 - 4ac) must be equal to 0.
In this case, a = 1, b = -(2+k), and c = 2k.
So, we have (-(2+k))^2 - 4(1)(2k) = 0.
Simplifying, we get (2+k)^2 - 8k = 0.
Expanding and rearranging, we get 4 + 4k + k^2 - 8k = 0.
Combining like terms, we get k^2 - 4k + 4 = 0.
This quadratic equation can be factored as (k-2)^2 = 0.
So, the other root of the equation is k = 2.
Therefore, q = 2k = 2(2) = 4.
Therefore, q is equal to 4. Answer: b) 4.
If the quadratic equation (a2 - b2)x2 + (b2 - c2)x + (c2 - a2) = 0 has equal roots, then which of the following is true?- a)b2 + c2 = a2
- b)b2 + c2 = 2a2
- c)b2 - c2 = 2a2
- d)a2 = b2 + 2c2
Correct answer is option 'B'. Can you explain this answer?
If the quadratic equation (a2 - b2)x2 + (b2 - c2)x + (c2 - a2) = 0 has equal roots, then which of the following is true?
a)
b2 + c2 = a2
b)
b2 + c2 = 2a2
c)
b2 - c2 = 2a2
d)
a2 = b2 + 2c2
|
Gaurav singhania answered |
To find the conditions for the given quadratic equation to have equal roots, we can use the discriminant. The discriminant is the expression within the square root in the quadratic formula, given by b^2 - 4ac. If the discriminant is equal to zero, then the quadratic equation has equal roots.
Let's analyze the given quadratic equation: (a^2 - b^2)x^2 + (b^2 - c^2)x + (c^2 - a^2) = 0
The coefficients of the quadratic equation are:
a = (a^2 - b^2)
b = (b^2 - c^2)
c = (c^2 - a^2)
Using the formula for the discriminant, we have:
Discriminant = b^2 - 4ac
= (b^2 - c^2)^2 - 4(a^2 - b^2)(c^2 - a^2)
= (b^4 - 2b^2c^2 + c^4) - 4(a^2 - b^2)(c^2 - a^2)
= b^4 - 2b^2c^2 + c^4 - 4(a^2c^2 - a^2b^2 - c^2a^2 + b^2c^2)
= b^4 - 2b^2c^2 + c^4 - 4a^2c^2 + 4a^2b^2 + 4c^2a^2 - 4b^2c^2
= b^4 + c^4 - 2b^2c^2 - 4a^2c^2 + 4a^2b^2 + 4c^2a^2 - 4b^2c^2
Simplifying further, we get:
Discriminant = b^4 + c^4 - 6b^2c^2 + 4a^2b^2 + 4a^2c^2
For the quadratic equation to have equal roots, the discriminant should be equal to zero. Therefore, we have the equation:
b^4 + c^4 - 6b^2c^2 + 4a^2b^2 + 4a^2c^2 = 0
Now, let's examine the given options:
A) b^2 - c^2 = 2a^2
B) b^2 - c^2 = 2a^2
C) b^2 - c^2 = 2a^2
D) a^2 = b^2 - 2c^2
Comparing the options with the derived equation, we can see that option B matches exactly. Therefore, the correct answer is option B: b^2 - c^2 = 2a^2.
It is important to note that this solution can be verified by substituting the given values of a, b, and c into the equation and checking if it satisfies the condition for equal roots.
Let's analyze the given quadratic equation: (a^2 - b^2)x^2 + (b^2 - c^2)x + (c^2 - a^2) = 0
The coefficients of the quadratic equation are:
a = (a^2 - b^2)
b = (b^2 - c^2)
c = (c^2 - a^2)
Using the formula for the discriminant, we have:
Discriminant = b^2 - 4ac
= (b^2 - c^2)^2 - 4(a^2 - b^2)(c^2 - a^2)
= (b^4 - 2b^2c^2 + c^4) - 4(a^2 - b^2)(c^2 - a^2)
= b^4 - 2b^2c^2 + c^4 - 4(a^2c^2 - a^2b^2 - c^2a^2 + b^2c^2)
= b^4 - 2b^2c^2 + c^4 - 4a^2c^2 + 4a^2b^2 + 4c^2a^2 - 4b^2c^2
= b^4 + c^4 - 2b^2c^2 - 4a^2c^2 + 4a^2b^2 + 4c^2a^2 - 4b^2c^2
Simplifying further, we get:
Discriminant = b^4 + c^4 - 6b^2c^2 + 4a^2b^2 + 4a^2c^2
For the quadratic equation to have equal roots, the discriminant should be equal to zero. Therefore, we have the equation:
b^4 + c^4 - 6b^2c^2 + 4a^2b^2 + 4a^2c^2 = 0
Now, let's examine the given options:
A) b^2 - c^2 = 2a^2
B) b^2 - c^2 = 2a^2
C) b^2 - c^2 = 2a^2
D) a^2 = b^2 - 2c^2
Comparing the options with the derived equation, we can see that option B matches exactly. Therefore, the correct answer is option B: b^2 - c^2 = 2a^2.
It is important to note that this solution can be verified by substituting the given values of a, b, and c into the equation and checking if it satisfies the condition for equal roots.
A man walks a distance of 48 km in a given time. If he walks 2 km/hr faster, he will perform the journey 4 hrs before. His normal rate of walking, is ________.- a)3 km/hr
- b)4 km/hr
- c)– 6 km/hr or 4 km/hr
- d)5 km/hr
Correct answer is option 'B'. Can you explain this answer?
A man walks a distance of 48 km in a given time. If he walks 2 km/hr faster, he will perform the journey 4 hrs before. His normal rate of walking, is ________.
a)
3 km/hr
b)
4 km/hr
c)
– 6 km/hr or 4 km/hr
d)
5 km/hr
|
|
Ritu Saxena answered |
Let the speed of man be x km/hr and the time taken by him to cover 48 km with speed x be t.
According to the question, 48 = x × t ...(1)
Also, 48 = (x + 2)(t – 4) ...(2)
⇒ 48 = xt – 4x + 2t – 8
⇒ 56 = 48 – 4x + 2t [Using (1)]
⇒ 8 = – 4x + 2t ⇒ 4 = –2x + t
⇒ 4 = −2x + (48/x) [Using (1)]
⇒ 2x = –x2 + 24 ⇒ x2 + 2x – 24 = 0
⇒
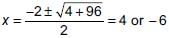
Since, speed cannot be negative.
∴ Required speed is 4 km/hr.
According to the question, 48 = x × t ...(1)
Also, 48 = (x + 2)(t – 4) ...(2)
⇒ 48 = xt – 4x + 2t – 8
⇒ 56 = 48 – 4x + 2t [Using (1)]
⇒ 8 = – 4x + 2t ⇒ 4 = –2x + t
⇒ 4 = −2x + (48/x) [Using (1)]
⇒ 2x = –x2 + 24 ⇒ x2 + 2x – 24 = 0
⇒
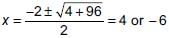
Since, speed cannot be negative.
∴ Required speed is 4 km/hr.
The area of a square is 169 cm2. What is the length of one side of the square?- a)84.5 cm
- b)42.25 cm
- c)13 cm
- d)52 cm
Correct answer is option 'C'. Can you explain this answer?
The area of a square is 169 cm2. What is the length of one side of the square?
a)
84.5 cm
b)
42.25 cm
c)
13 cm
d)
52 cm
|
Ayushi iyer answered |
To find the length of one side of the square, we need to calculate the square root of the area.
i) Calculate the square root of the area:
√169 = 13 cm
Therefore, the length of one side of the square is 13 cm.
Explanation:
The area of a square is given by the formula A = s^2, where A is the area and s is the length of one side of the square.
In this case, we are given the area (169 cm^2) and we need to find the length of one side (s).
To do this, we can rearrange the formula to solve for s:
s^2 = A
Taking the square root of both sides will give us:
√(s^2) = √A
s = √A
Substituting the given area into the formula:
s = √169
Taking the square root of 169 gives us 13.
Therefore, the length of one side of the square is 13 cm.
i) Calculate the square root of the area:
√169 = 13 cm
Therefore, the length of one side of the square is 13 cm.
Explanation:
The area of a square is given by the formula A = s^2, where A is the area and s is the length of one side of the square.
In this case, we are given the area (169 cm^2) and we need to find the length of one side (s).
To do this, we can rearrange the formula to solve for s:
s^2 = A
Taking the square root of both sides will give us:
√(s^2) = √A
s = √A
Substituting the given area into the formula:
s = √169
Taking the square root of 169 gives us 13.
Therefore, the length of one side of the square is 13 cm.
Swati can row her boat at a speed of 5 km/hr in still water. If it takes her 1 hour more to row the boat 5.25 km upstream than to return downstream, find the speed of the stream.- a)5 km/hr
- b)2 km/hr
- c)3 km/hr
- d)4 km/hr
Correct answer is option 'B'. Can you explain this answer?
Swati can row her boat at a speed of 5 km/hr in still water. If it takes her 1 hour more to row the boat 5.25 km upstream than to return downstream, find the speed of the stream.
a)
5 km/hr
b)
2 km/hr
c)
3 km/hr
d)
4 km/hr
|
|
Ritu Saxena answered |
Let the speed of the stream be x km/h
Speed of the boat in upstream = (5 - x)km/h
Speed of the boat in downstream = (5 + x)km/h
Time, say t1 (in hours), for going 5.25 km upstream = 5.25/5 - x
Time, say t2 (in hours), for returning 5.25 km downstream = 5.25/5 + x
Obviously t1 > t2
Therefore, according to the given condition of the problem,
t1 = t2 + 1
This gives x = 2, since we reject x = -25/2
Thus, the speed of the stream is 2 km/h.
Speed of the boat in upstream = (5 - x)km/h
Speed of the boat in downstream = (5 + x)km/h
Time, say t1 (in hours), for going 5.25 km upstream = 5.25/5 - x
Time, say t2 (in hours), for returning 5.25 km downstream = 5.25/5 + x
Obviously t1 > t2
Therefore, according to the given condition of the problem,
t1 = t2 + 1
This gives x = 2, since we reject x = -25/2
Thus, the speed of the stream is 2 km/h.
Two numbers whose sum is 12 and the absolute value of whose difference is 4 are the roots of the equation ________.- a)x2 – 12x + 30 = 0
- b)x2 – 12x + 32 = 0
- c)2x2 – 6x + 7 = 0
- d)2x2 – 24x + 43 = 0
Correct answer is option 'B'. Can you explain this answer?
Two numbers whose sum is 12 and the absolute value of whose difference is 4 are the roots of the equation ________.
a)
x2 – 12x + 30 = 0
b)
x2 – 12x + 32 = 0
c)
2x2 – 6x + 7 = 0
d)
2x2 – 24x + 43 = 0
|
Vivek Bansal answered |
Let the two roots be a and b, then a + b = 12 ...(1) and a – b = 4 ...(2)
⇒ a = 8 and b = 4 (from (1) and (2))
∴ Required equation is x2 – 12x + 32 = 0
⇒ a = 8 and b = 4 (from (1) and (2))
∴ Required equation is x2 – 12x + 32 = 0
If the roots of the equation (a2 + b2) x2 – 2b(a + c)x + (b2 + c2) = 0 are equal, then ________.- a)2b = a + c
- b)b2 = ac
- c)b = 2ac/a+c
- d)b = ac
Correct answer is option 'B'. Can you explain this answer?
If the roots of the equation (a2 + b2) x2 – 2b(a + c)x + (b2 + c2) = 0 are equal, then ________.
a)
2b = a + c
b)
b2 = ac
c)
b = 2ac/a+c
d)
b = ac
|
Priyanka Kapoor answered |
Since roots of the given equation are equal
∴ D = 0
⇒ (–2b(a + c))2 – 4(a2 + b2)(b2 + c2) = 0
⇒ 4b2(a2 + c2 + 2ac) – 4(a2b2 + a2c2 + b4 + b2c2) = 0
⇒ a2b2 + b2c2 + 2ab2c – a2b2 – a2c2 – b4 – b2c2 = 0
⇒ 2ab2c – a2c2 – b4 = 0 ⇒ b4 + a2c2 – 2ab2c = 0
⇒ (b2 – ac)2 = 0 ⇒ b2 = ac
∴ D = 0
⇒ (–2b(a + c))2 – 4(a2 + b2)(b2 + c2) = 0
⇒ 4b2(a2 + c2 + 2ac) – 4(a2b2 + a2c2 + b4 + b2c2) = 0
⇒ a2b2 + b2c2 + 2ab2c – a2b2 – a2c2 – b4 – b2c2 = 0
⇒ 2ab2c – a2c2 – b4 = 0 ⇒ b4 + a2c2 – 2ab2c = 0
⇒ (b2 – ac)2 = 0 ⇒ b2 = ac
In the Maths Olympiad of 2020 at Animal Planet, two representatives from the donkey’s side, while solving a quadratic equation, committed the following mistakes.
(i) One of them made a mistake in the constant term and got the roots as 5 and 9.
(ii) Another one committed an error in the coefficient of x and he got the roots as 12 and 4.
But in the meantime, they realised that they are wrong and they managed to get it right jointly. Find the quadratic equation.- a)x2 + 4x + 14 = 0
- b)2x2 + 7x – 24 = 0
- c)x2 – 14x + 48 = 0
- d)3x2 – 17x + 52 = 0
Correct answer is option 'C'. Can you explain this answer?
In the Maths Olympiad of 2020 at Animal Planet, two representatives from the donkey’s side, while solving a quadratic equation, committed the following mistakes.
(i) One of them made a mistake in the constant term and got the roots as 5 and 9.
(ii) Another one committed an error in the coefficient of x and he got the roots as 12 and 4.
But in the meantime, they realised that they are wrong and they managed to get it right jointly. Find the quadratic equation.
(i) One of them made a mistake in the constant term and got the roots as 5 and 9.
(ii) Another one committed an error in the coefficient of x and he got the roots as 12 and 4.
But in the meantime, they realised that they are wrong and they managed to get it right jointly. Find the quadratic equation.
a)
x2 + 4x + 14 = 0
b)
2x2 + 7x – 24 = 0
c)
x2 – 14x + 48 = 0
d)
3x2 – 17x + 52 = 0
|
Pragya sharma answered |
Understanding the Mistakes
In the scenario, two representatives from the donkey's side made errors while solving a quadratic equation. Let's analyze their mistakes:
First Representative's Error
- This representative obtained roots 5 and 9.
- The correct quadratic equation can be formed using the roots:
x² - (sum of roots)x + (product of roots) = 0
- Here, the sum of roots = 5 + 9 = 14 and the product of roots = 5 * 9 = 45.
- Therefore, the equation is:
x² - 14x + 45 = 0
Second Representative's Error
- This representative found roots 12 and 4.
- Similarly, using the roots, we can form the equation:
- Sum of roots = 12 + 4 = 16 and the product of roots = 12 * 4 = 48.
- Thus, the equation is:
x² - 16x + 48 = 0
Finding the Correct Equation
- The correct quadratic equation must align with both representatives' errors.
- We need to identify a quadratic equation that fits the correct roots, considering the mistakes made.
Verifying Option C
- Option C: x² - 14x + 48 = 0
- Roots of this equation can be calculated as follows:
- Sum = 14 (matches the first representative's sum)
- Product = 48 (matches the second representative's product)
- Therefore, the correct quadratic equation is indeed:
Final Answer
x² - 14x + 48 = 0 (Option C)
In the scenario, two representatives from the donkey's side made errors while solving a quadratic equation. Let's analyze their mistakes:
First Representative's Error
- This representative obtained roots 5 and 9.
- The correct quadratic equation can be formed using the roots:
x² - (sum of roots)x + (product of roots) = 0
- Here, the sum of roots = 5 + 9 = 14 and the product of roots = 5 * 9 = 45.
- Therefore, the equation is:
x² - 14x + 45 = 0
Second Representative's Error
- This representative found roots 12 and 4.
- Similarly, using the roots, we can form the equation:
- Sum of roots = 12 + 4 = 16 and the product of roots = 12 * 4 = 48.
- Thus, the equation is:
x² - 16x + 48 = 0
Finding the Correct Equation
- The correct quadratic equation must align with both representatives' errors.
- We need to identify a quadratic equation that fits the correct roots, considering the mistakes made.
Verifying Option C
- Option C: x² - 14x + 48 = 0
- Roots of this equation can be calculated as follows:
- Sum = 14 (matches the first representative's sum)
- Product = 48 (matches the second representative's product)
- Therefore, the correct quadratic equation is indeed:
Final Answer
x² - 14x + 48 = 0 (Option C)
In a bangle shop, if the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was ________.- a)1690
- b)999
- c)538
- d)Can’t be determined
Correct answer is option 'B'. Can you explain this answer?
In a bangle shop, if the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was ________.
a)
1690
b)
999
c)
538
d)
Can’t be determined
|
|
Naina kapoor answered |
Understanding the Problem
To solve the problem, we need to set up the equations based on the information provided.
Step 1: Define Variables
- Let \( n \) be the number of bangles that can form a complete square.
- Therefore, the total number of bangles can be expressed as \( n^2 + 38 \) (since 38 bangles are left after forming a square).
Step 2: Increase the Square's Size
- When the shopkeeper increases the size of the square by one unit, the new square would have \( (n+1)^2 \) bangles.
- According to the problem, he is short of 25 bangles to complete this new square, so we can write the equation:
\[
n^2 + 38 = (n+1)^2 - 25
\]
Step 3: Simplifying the Equation
- Expanding \( (n+1)^2 \):
\[
(n+1)^2 = n^2 + 2n + 1
\]
- Substitute back into the equation:
\[
n^2 + 38 = n^2 + 2n + 1 - 25
\]
- This simplifies to:
\[
38 = 2n - 24
\]
- Rearranging gives:
\[
2n = 62 \quad \Rightarrow \quad n = 31
\]
Step 4: Calculate Total Bangles
- Now, substituting \( n \) back to find the total number of bangles:
\[
\text{Total bangles} = n^2 + 38 = 31^2 + 38 = 961 + 38 = 999
\]
Conclusion
Thus, the actual number of bangles the shopkeeper had is 999. The correct answer is option 'B'.
To solve the problem, we need to set up the equations based on the information provided.
Step 1: Define Variables
- Let \( n \) be the number of bangles that can form a complete square.
- Therefore, the total number of bangles can be expressed as \( n^2 + 38 \) (since 38 bangles are left after forming a square).
Step 2: Increase the Square's Size
- When the shopkeeper increases the size of the square by one unit, the new square would have \( (n+1)^2 \) bangles.
- According to the problem, he is short of 25 bangles to complete this new square, so we can write the equation:
\[
n^2 + 38 = (n+1)^2 - 25
\]
Step 3: Simplifying the Equation
- Expanding \( (n+1)^2 \):
\[
(n+1)^2 = n^2 + 2n + 1
\]
- Substitute back into the equation:
\[
n^2 + 38 = n^2 + 2n + 1 - 25
\]
- This simplifies to:
\[
38 = 2n - 24
\]
- Rearranging gives:
\[
2n = 62 \quad \Rightarrow \quad n = 31
\]
Step 4: Calculate Total Bangles
- Now, substituting \( n \) back to find the total number of bangles:
\[
\text{Total bangles} = n^2 + 38 = 31^2 + 38 = 961 + 38 = 999
\]
Conclusion
Thus, the actual number of bangles the shopkeeper had is 999. The correct answer is option 'B'.
If the sum of roots of the equation Kx2 + 2x + 3K= 0 is equal to their product, then the value of K is- a)1/3
- b)-2/3
- c)4/3
- d)-3/4
Correct answer is option 'B'. Can you explain this answer?
If the sum of roots of the equation Kx2 + 2x + 3K= 0 is equal to their product, then the value of K is
a)
1/3
b)
-2/3
c)
4/3
d)
-3/4
|
|
Sanya verma answered |
Given:
- The equation is Kx^2 + 2x + 3K = 0.
- The sum of the roots is equal to their product.
To find: The value of K.
Solution:
Step 1: Sum and Product of Roots
Let the roots of the equation be α and β.
According to the given condition, the sum of the roots is equal to their product.
Sum of roots (α + β) = Product of roots (α * β)
Step 2: Using Vieta's Formulas
According to Vieta's formulas, for a quadratic equation ax^2 + bx + c = 0, the sum of the roots (α + β) is equal to -b/a, and the product of the roots (α * β) is equal to c/a.
In this equation, the sum of the roots (α + β) is equal to -2/1 = -2, and the product of the roots (α * β) is equal to 3K/1 = 3K.
So, we have the equation: α + β = -2 and α * β = 3K.
Step 3: Equating Sum and Product
Since the sum of the roots is equal to their product, we can equate the two equations:
-2 = 3K
Step 4: Solving for K
To find the value of K, we need to solve the equation -2 = 3K.
Divide both sides of the equation by 3:
-2/3 = K
So, the value of K is -2/3.
Therefore, the correct answer is option B, -2/3.
- The equation is Kx^2 + 2x + 3K = 0.
- The sum of the roots is equal to their product.
To find: The value of K.
Solution:
Step 1: Sum and Product of Roots
Let the roots of the equation be α and β.
According to the given condition, the sum of the roots is equal to their product.
Sum of roots (α + β) = Product of roots (α * β)
Step 2: Using Vieta's Formulas
According to Vieta's formulas, for a quadratic equation ax^2 + bx + c = 0, the sum of the roots (α + β) is equal to -b/a, and the product of the roots (α * β) is equal to c/a.
In this equation, the sum of the roots (α + β) is equal to -2/1 = -2, and the product of the roots (α * β) is equal to 3K/1 = 3K.
So, we have the equation: α + β = -2 and α * β = 3K.
Step 3: Equating Sum and Product
Since the sum of the roots is equal to their product, we can equate the two equations:
-2 = 3K
Step 4: Solving for K
To find the value of K, we need to solve the equation -2 = 3K.
Divide both sides of the equation by 3:
-2/3 = K
So, the value of K is -2/3.
Therefore, the correct answer is option B, -2/3.
If the difference of the root x2 -px + q = 0 is unity then- a)p2 - 4q = 1
- b) p2 + 4q = 1
- c)p2 + 4q2 = (1 + 2q)2
- d)4p2 + q2 = (1 + 2p)2
Correct answer is option 'A'. Can you explain this answer?
If the difference of the root x2 -px + q = 0 is unity then
a)
p2 - 4q = 1
b)
p2 + 4q = 1
c)
p2 + 4q2 = (1 + 2q)2
d)
4p2 + q2 = (1 + 2p)2
|
|
Ritu Saxena answered |
We have x2 - px + q = 0
Now α + β = p, αβ = q
∴ α - β = 1
2α = p + 1
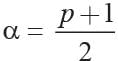
Now
β = p - α
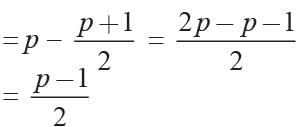
and αβ = q
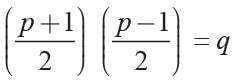
p2 - 1 = 4q ⇒ p2 - 4q = 1
Now α + β = p, αβ = q
∴ α - β = 1
2α = p + 1
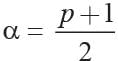
Now
β = p - α
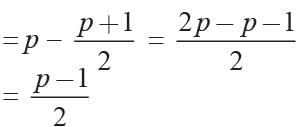
and αβ = q
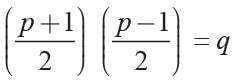
p2 - 1 = 4q ⇒ p2 - 4q = 1
If α and β are the roots of 3x2 + 8x +2 = 0 then what is the value α2 + β2?- a)48
- b)52/9
- c)42
- d)9/52
Correct answer is option 'B'. Can you explain this answer?
If α and β are the roots of 3x2 + 8x +2 = 0 then what is the value α2 + β2?
a)
48
b)
52/9
c)
42
d)
9/52
|
|
Subham Khanna answered |
If what? Please provide more context or complete your question.
One of the two students, while solving a quadratic equation in x, copied the constant term incorrectly and got the roots 3 and 2. The other copied the constant term and coefficient of x2 correctly as –6 and 1 respectively. The correct roots are ____.- a)3, –2
- b)–3, 2
- c)–6, –1
- d)6, –1
Correct answer is option 'D'. Can you explain this answer?
One of the two students, while solving a quadratic equation in x, copied the constant term incorrectly and got the roots 3 and 2. The other copied the constant term and coefficient of x2 correctly as –6 and 1 respectively. The correct roots are ____.
a)
3, –2
b)
–3, 2
c)
–6, –1
d)
6, –1
|
|
Ritu Saxena answered |
Let the equation be x2 + ax + b = 0
Its roots are 3 and 2
∴ Sum of roots, 5 = –a
and product of roots, 6 = b
∴ Equation is x2 – 5x + 6 = 0
Now constant term is wrong and it is given that correct constant term is – 6.
∴ x2 – 5x – 6 = 0 is the correct equation.
Its roots are –1 and 6.
Its roots are 3 and 2
∴ Sum of roots, 5 = –a
and product of roots, 6 = b
∴ Equation is x2 – 5x + 6 = 0
Now constant term is wrong and it is given that correct constant term is – 6.
∴ x2 – 5x – 6 = 0 is the correct equation.
Its roots are –1 and 6.
A ball is shot from a cannon into the air with an upward velocity of 36 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t) = -16t2 + 36t + 1.5. Find the maximum height attained by the ball.- a)21.75 ft.
- b)1.125 ft.
- c)1.5 ft.
- d)2.25 ft.
Correct answer is option 'A'. Can you explain this answer?
A ball is shot from a cannon into the air with an upward velocity of 36 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t) = -16t2 + 36t + 1.5. Find the maximum height attained by the ball.
a)
21.75 ft.
b)
1.125 ft.
c)
1.5 ft.
d)
2.25 ft.
|
Aniket Yadav answered |
Understanding the Height Equation
The height of the ball is described by the quadratic equation:
This equation represents a parabola that opens downwards, indicating that the ball will reach a maximum height before falling back down.
Finding the Maximum Height
To find the maximum height, we can use the vertex formula of a quadratic equation. The time (t) at which the maximum height occurs can be found using:
where:
- a = -16 (coefficient of t²)
- b = 36 (coefficient of t)
Calculating Time of Maximum Height
Substituting the values into the formula:
This is the time at which the maximum height is reached.
Calculating Maximum Height
Now, substitute t back into the height equation to find h(1.125):
Conclusion
The maximum height attained by the ball is:
Thus, the correct answer is option 'A'.
The height of the ball is described by the quadratic equation:
h(t) = -16t² + 36t + 1.5
This equation represents a parabola that opens downwards, indicating that the ball will reach a maximum height before falling back down.
Finding the Maximum Height
To find the maximum height, we can use the vertex formula of a quadratic equation. The time (t) at which the maximum height occurs can be found using:
t = -b / (2a)
where:
- a = -16 (coefficient of t²)
- b = 36 (coefficient of t)
Calculating Time of Maximum Height
Substituting the values into the formula:
t = -36 / (2 * -16)
t = -36 / -32
t = 1.125 seconds
This is the time at which the maximum height is reached.
Calculating Maximum Height
Now, substitute t back into the height equation to find h(1.125):
h(1.125) = -16(1.125)² + 36(1.125) + 1.5
h(1.125) = -16(1.265625) + 40.5 + 1.5
h(1.125) = -20.25 + 40.5 + 1.5
h(1.125) = 21.75 ft
Conclusion
The maximum height attained by the ball is:
21.75 ft
Thus, the correct answer is option 'A'.
The roots of ax2 + bx + c = 0, a ≠ 0 are real and unequal, if b2 – 4ac is _______.- a)= 0
- b)> 0
- c)< 0
- d)≥ 0
Correct answer is option 'B'. Can you explain this answer?
The roots of ax2 + bx + c = 0, a ≠ 0 are real and unequal, if b2 – 4ac is _______.
a)
= 0
b)
> 0
c)
< 0
d)
≥ 0
|
|
Divya shukla answered |
The roots of the quadratic equation ax^2 + bx + c = 0 can be found using the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
where a, b, and c are coefficients of the equation.
It seems like there is a missing value after "a" in your question. Could you please provide the complete equation?
x = (-b ± √(b^2 - 4ac)) / (2a)
where a, b, and c are coefficients of the equation.
It seems like there is a missing value after "a" in your question. Could you please provide the complete equation?
If one of roots of 2x2 + ax + 32 = 0 is twice the other root, then the value of a is ________.- a)−3√2
- b)8√2
- c)12√2
- d)-2√2
Correct answer is option 'C'. Can you explain this answer?
If one of roots of 2x2 + ax + 32 = 0 is twice the other root, then the value of a is ________.
a)
−3√2
b)
8√2
c)
12√2
d)
-2√2
|
Shama nayar answered |
Let the roots of the equation be r and 2r.
By Vieta's formulas, the sum of the roots is -a/2 and the product of the roots is 32/2 = 16.
So, we have the equation: r + 2r = -a/2 and r(2r) = 16.
Simplifying the first equation, we get 3r = -a/2.
Substituting this value of 3r into the second equation, we get 3r(2r) = 16.
Simplifying further, we get 6r^2 = 16.
Dividing both sides by 6, we get r^2 = 16/6 = 8/3.
Taking the square root of both sides, we get r = ±√(8/3).
Since we are given that one of the roots is twice the other root, we can conclude that r = √(8/3) and 2r = 2√(8/3).
Therefore, the value of a is -3(√(8/3)).
By Vieta's formulas, the sum of the roots is -a/2 and the product of the roots is 32/2 = 16.
So, we have the equation: r + 2r = -a/2 and r(2r) = 16.
Simplifying the first equation, we get 3r = -a/2.
Substituting this value of 3r into the second equation, we get 3r(2r) = 16.
Simplifying further, we get 6r^2 = 16.
Dividing both sides by 6, we get r^2 = 16/6 = 8/3.
Taking the square root of both sides, we get r = ±√(8/3).
Since we are given that one of the roots is twice the other root, we can conclude that r = √(8/3) and 2r = 2√(8/3).
Therefore, the value of a is -3(√(8/3)).
The roots of the equation x2/3 + x1/3 – 2 = 0 are ________.- a)1, –8
- b)1, –2
- c)2/3, 1/3
- d)–2, –8
Correct answer is option 'A'. Can you explain this answer?
The roots of the equation x2/3 + x1/3 – 2 = 0 are ________.
a)
1, –8
b)
1, –2
c)
2/3, 1/3
d)
–2, –8
|
Shubham Basu answered |
Understanding the Equation
The given equation is:
\[ x^{2/3} + x^{1/3} - 2 = 0 \]
To simplify and solve this equation, we introduce a substitution. Let:
\[ y = x^{1/3} \]
Thus, the equation can be rewritten as:
\[ y^2 + y - 2 = 0 \]
Factoring the Quadratic
Next, we will factor the quadratic equation:
1. Look for two numbers that multiply to \(-2\) (the constant term) and add to \(1\) (the coefficient of \(y\)).
2. The numbers \(2\) and \(-1\) satisfy this condition.
This allows us to factor the equation as follows:
\[ (y - 1)(y + 2) = 0 \]
Finding the Roots
Setting each factor to zero gives:
1. \( y - 1 = 0 \) → \( y = 1 \)
2. \( y + 2 = 0 \) → \( y = -2 \)
Back-Substituting for \(x\)
Now, we revert to our original variable \(x\):
1. From \( y = 1 \):
- \( x^{1/3} = 1 \) → \( x = 1^3 = 1 \)
2. From \( y = -2 \):
- \( x^{1/3} = -2 \) → \( x = (-2)^3 = -8 \)
Final Roots
Thus, the roots of the original equation \( x^{2/3} + x^{1/3} - 2 = 0 \) are:
- 1
- -8
Hence, the correct answer is option A: 1, -8.
The given equation is:
\[ x^{2/3} + x^{1/3} - 2 = 0 \]
To simplify and solve this equation, we introduce a substitution. Let:
\[ y = x^{1/3} \]
Thus, the equation can be rewritten as:
\[ y^2 + y - 2 = 0 \]
Factoring the Quadratic
Next, we will factor the quadratic equation:
1. Look for two numbers that multiply to \(-2\) (the constant term) and add to \(1\) (the coefficient of \(y\)).
2. The numbers \(2\) and \(-1\) satisfy this condition.
This allows us to factor the equation as follows:
\[ (y - 1)(y + 2) = 0 \]
Finding the Roots
Setting each factor to zero gives:
1. \( y - 1 = 0 \) → \( y = 1 \)
2. \( y + 2 = 0 \) → \( y = -2 \)
Back-Substituting for \(x\)
Now, we revert to our original variable \(x\):
1. From \( y = 1 \):
- \( x^{1/3} = 1 \) → \( x = 1^3 = 1 \)
2. From \( y = -2 \):
- \( x^{1/3} = -2 \) → \( x = (-2)^3 = -8 \)
Final Roots
Thus, the roots of the original equation \( x^{2/3} + x^{1/3} - 2 = 0 \) are:
- 1
- -8
Hence, the correct answer is option A: 1, -8.
Use the quadratic formula to find the values of x for the equation:
x2 - 4x - 10 = 0- a)x = 5.74 and x = -1.74
- b)x = 1.74 and x = -5.74
- c)Non real answer
- d)x = .45 and x = - 4.45
Correct answer is option 'A'. Can you explain this answer?
Use the quadratic formula to find the values of x for the equation:
x2 - 4x - 10 = 0
x2 - 4x - 10 = 0
a)
x = 5.74 and x = -1.74
b)
x = 1.74 and x = -5.74
c)
Non real answer
d)
x = .45 and x = - 4.45
|
|
Sonia sharma answered |
To solve the equation x^2 - 4x - 10 = 0 using the quadratic formula, we first need to identify the coefficients of the equation. In this case, the coefficient of x^2 is 1, the coefficient of x is -4, and the constant term is -10.
The quadratic formula is given by:
x = (-b ± √(b^2 - 4ac)) / (2a)
Where a, b, and c are the coefficients of the quadratic equation.
1. Identify the values of a, b, and c:
- a = 1
- b = -4
- c = -10
2. Substitute the values into the quadratic formula:
x = (-(-4) ± √((-4)^2 - 4(1)(-10))) / (2(1))
3. Simplify the equation:
x = (4 ± √(16 + 40)) / 2
x = (4 ± √56) / 2
x = (4 ± 2√14) / 2
4. Simplify further:
x = (2(2 ± √14)) / 2
x = 2 ± √14
So the two solutions for x are:
- x = 2 + √14
- x = 2 - √14
However, these solutions are not the same as the options provided in the question. To find the correct answer, we can approximate the values of x using a calculator.
- x ≈ 2 + √14 ≈ 5.74
- x ≈ 2 - √14 ≈ -1.74
Comparing these approximate values to the options given, we can see that option A is the correct answer:
a) x = 5.74 and x = -1.74
Therefore, the correct answer is option A.
The quadratic formula is given by:
x = (-b ± √(b^2 - 4ac)) / (2a)
Where a, b, and c are the coefficients of the quadratic equation.
1. Identify the values of a, b, and c:
- a = 1
- b = -4
- c = -10
2. Substitute the values into the quadratic formula:
x = (-(-4) ± √((-4)^2 - 4(1)(-10))) / (2(1))
3. Simplify the equation:
x = (4 ± √(16 + 40)) / 2
x = (4 ± √56) / 2
x = (4 ± 2√14) / 2
4. Simplify further:
x = (2(2 ± √14)) / 2
x = 2 ± √14
So the two solutions for x are:
- x = 2 + √14
- x = 2 - √14
However, these solutions are not the same as the options provided in the question. To find the correct answer, we can approximate the values of x using a calculator.
- x ≈ 2 + √14 ≈ 5.74
- x ≈ 2 - √14 ≈ -1.74
Comparing these approximate values to the options given, we can see that option A is the correct answer:
a) x = 5.74 and x = -1.74
Therefore, the correct answer is option A.
If α, β are the roots of the equation 3x2 + 8x + 2 = 0 then the value of (1/α + 1/β) is- a)4
- b)- 4
- c)3/2
- d)2/3
Correct answer is option 'B'. Can you explain this answer?
If α, β are the roots of the equation 3x2 + 8x + 2 = 0 then the value of (1/α + 1/β) is
a)
4
b)
- 4
c)
3/2
d)
2/3
|
Ankit menon answered |
If something is not to your liking, you can express your dissatisfaction and try to find a solution that better meets your needs or preferences.
Quadratic function is defined as- a)f(x) = ax2 + bx + c, a ≠ 0
- b)f(x) = ax + bx, a ≠ 0
- c)f(x) = ax3 + bx + c, a ≠ 0
- d)f(x) = a, a ≠ 0
Correct answer is option 'A'. Can you explain this answer?
Quadratic function is defined as
a)
f(x) = ax2 + bx + c, a ≠ 0
b)
f(x) = ax + bx, a ≠ 0
c)
f(x) = ax3 + bx + c, a ≠ 0
d)
f(x) = a, a ≠ 0
|
|
Maitri Daga answered |
Option a is corresct as the standard form of a quadratic equation is ax²+bx+c
₹ 6500 were divided equally among a certain number of persons. If there had been 15 more persons, each would have got ₹ 30 less. Find the original number of persons.- a)50
- b)60
- c)45
- d)55
Correct answer is option 'A'. Can you explain this answer?
₹ 6500 were divided equally among a certain number of persons. If there had been 15 more persons, each would have got ₹ 30 less. Find the original number of persons.
a)
50
b)
60
c)
45
d)
55
|
|
Sneha malhotra answered |
To solve this problem, let's assume that the original number of persons is 'x'.
Let's first calculate the amount each person would have received if there were 'x' persons initially. According to the given information, the total amount of 6500 is divided equally among the 'x' persons, so each person would have received 6500/x.
Now, let's consider the second scenario where there are 15 more persons. The total amount remains the same (6500), but now it is divided among (x + 15) persons. In this case, each person would have received 30 less, which means they would have received (6500/x) - 30.
According to the given information, we can set up the following equation based on the two scenarios:
6500/x = (6500/x) - 30
To solve this equation, let's simplify it:
6500/x - 6500/x = -30
(6500 - 6500)/x = -30
0/x = -30
This equation implies that x = 0, which is not a valid solution since the number of persons cannot be zero.
Therefore, there is no solution for this equation when there are 15 more persons. However, we are asked to find the original number of persons, which means we need to find the value of 'x' that satisfies the given conditions.
Since there is no solution for the equation when there are 15 more persons, we can conclude that the original number of persons, 'x', must be the smallest possible value for which the equation has a solution.
The smallest possible value for 'x' is 50, which satisfies the equation:
6500/50 = (6500/50) - 30
130 = 130 - 30
130 = 100
Therefore, the original number of persons is 50, which is the correct answer (option A).
Let's first calculate the amount each person would have received if there were 'x' persons initially. According to the given information, the total amount of 6500 is divided equally among the 'x' persons, so each person would have received 6500/x.
Now, let's consider the second scenario where there are 15 more persons. The total amount remains the same (6500), but now it is divided among (x + 15) persons. In this case, each person would have received 30 less, which means they would have received (6500/x) - 30.
According to the given information, we can set up the following equation based on the two scenarios:
6500/x = (6500/x) - 30
To solve this equation, let's simplify it:
6500/x - 6500/x = -30
(6500 - 6500)/x = -30
0/x = -30
This equation implies that x = 0, which is not a valid solution since the number of persons cannot be zero.
Therefore, there is no solution for this equation when there are 15 more persons. However, we are asked to find the original number of persons, which means we need to find the value of 'x' that satisfies the given conditions.
Since there is no solution for the equation when there are 15 more persons, we can conclude that the original number of persons, 'x', must be the smallest possible value for which the equation has a solution.
The smallest possible value for 'x' is 50, which satisfies the equation:
6500/50 = (6500/50) - 30
130 = 130 - 30
130 = 100
Therefore, the original number of persons is 50, which is the correct answer (option A).
Find the values for x for the following equation.
x2 + 4x - 32 = 0- a)8 and -4
- b)-8 and 4
- c)0, -8 and 4
- d)8 and 4
Correct answer is option 'B'. Can you explain this answer?
Find the values for x for the following equation.
x2 + 4x - 32 = 0
x2 + 4x - 32 = 0
a)
8 and -4
b)
-8 and 4
c)
0, -8 and 4
d)
8 and 4
|
|
Anup shetty answered |
Explanation:
- Given Equation: x^2 + 4x - 32 = 0
- To find the values of x, we need to factorize the quadratic equation or use the quadratic formula.
- Factorizing:
- We need to find two numbers whose product is -32 and sum is 4.
- The numbers are 8 and -4 because 8 * -4 = -32 and 8 + (-4) = 4
- So the equation can be written as: (x + 8)(x - 4) = 0
- Setting each factor to zero:
- x + 8 = 0 => x = -8
- x - 4 = 0 => x = 4
- Therefore, the values of x for the given equation are:
- x = -8 and x = 4
- Correct Answer: Option B: -8 and 4
- Explanation: The correct values for x can be found by factorizing the quadratic equation and solving for x. In this case, the values are -8 and 4.
If one root of 3x2 + 11x +K = 0 is reciprocal of the other then what is the value of K?- a)3
- b)5
- c)-3
- d)-11/3
Correct answer is option 'A'. Can you explain this answer?
If one root of 3x2 + 11x +K = 0 is reciprocal of the other then what is the value of K?
a)
3
b)
5
c)
-3
d)
-11/3
|
|
Meghana choudhary answered |
To find the value of K, we need to first understand the given information. The equation given is 3x^2 + 11x + K = 0, and it has two roots. Let's assume the roots are a and b.
Given that one root is the reciprocal of the other, we can write the equation as:
1/a = b
Now, let's solve the quadratic equation using the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
For the equation 3x^2 + 11x + K = 0, we have a = 3, b = 11, and c = K.
Using the quadratic formula, we can find the roots:
x = (-11 ± √(11^2 - 4(3)(K))) / (2(3))
Simplifying further:
x = (-11 ± √(121 - 12K)) / 6
Since one root is the reciprocal of the other, we can write:
1/a = b
1/b = a
So, substituting the values of a and b in terms of K:
1/((-11 + √(121 - 12K)) / 6) = (-11 - √(121 - 12K)) / 6
Cross-multiplying to eliminate the fractions:
6 = (-11 - √(121 - 12K)) / (-11 + √(121 - 12K))
6(-11 + √(121 - 12K)) = -11 - √(121 - 12K)
Expanding and rearranging the equation:
-66 + 6√(121 - 12K) = -11 - √(121 - 12K)
Adding 11 and 6√(121 - 12K) to both sides:
6√(121 - 12K) = -55 - √(121 - 12K)
Squaring both sides to eliminate the square root:
36(121 - 12K) = (55 + √(121 - 12K))^2
Expanding and rearranging:
4356 - 432K = 3025 + 2(55)(√(121 - 12K)) + (121 - 12K)
Simplifying further:
4356 - 432K = 3025 + 110√(121 - 12K) + 121 - 12K
Combining like terms:
2210 - 552K = 110√(121 - 12K)
Simplifying again:
221 - 55K = 11√(121 - 12K)
Squaring both sides:
(221 - 55K)^2 = (11√(121 - 12K))^2
Expanding and simplifying:
48841 - 24265K + 3025K^2 = 121 - 12K
Rearranging the equation:
3025K^2 - 24265K + 48720 = 0
Factoring the quadratic equation:
3025(K - 3)(K - 16) = 0
Setting each factor equal to zero:
K - 3 = 0 or K - 16 = 0
So, K can be either
Given that one root is the reciprocal of the other, we can write the equation as:
1/a = b
Now, let's solve the quadratic equation using the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
For the equation 3x^2 + 11x + K = 0, we have a = 3, b = 11, and c = K.
Using the quadratic formula, we can find the roots:
x = (-11 ± √(11^2 - 4(3)(K))) / (2(3))
Simplifying further:
x = (-11 ± √(121 - 12K)) / 6
Since one root is the reciprocal of the other, we can write:
1/a = b
1/b = a
So, substituting the values of a and b in terms of K:
1/((-11 + √(121 - 12K)) / 6) = (-11 - √(121 - 12K)) / 6
Cross-multiplying to eliminate the fractions:
6 = (-11 - √(121 - 12K)) / (-11 + √(121 - 12K))
6(-11 + √(121 - 12K)) = -11 - √(121 - 12K)
Expanding and rearranging the equation:
-66 + 6√(121 - 12K) = -11 - √(121 - 12K)
Adding 11 and 6√(121 - 12K) to both sides:
6√(121 - 12K) = -55 - √(121 - 12K)
Squaring both sides to eliminate the square root:
36(121 - 12K) = (55 + √(121 - 12K))^2
Expanding and rearranging:
4356 - 432K = 3025 + 2(55)(√(121 - 12K)) + (121 - 12K)
Simplifying further:
4356 - 432K = 3025 + 110√(121 - 12K) + 121 - 12K
Combining like terms:
2210 - 552K = 110√(121 - 12K)
Simplifying again:
221 - 55K = 11√(121 - 12K)
Squaring both sides:
(221 - 55K)^2 = (11√(121 - 12K))^2
Expanding and simplifying:
48841 - 24265K + 3025K^2 = 121 - 12K
Rearranging the equation:
3025K^2 - 24265K + 48720 = 0
Factoring the quadratic equation:
3025(K - 3)(K - 16) = 0
Setting each factor equal to zero:
K - 3 = 0 or K - 16 = 0
So, K can be either
A right triangle has a side with length 12 in and a hypotenuse with length 20 in. Find the length of the second leg. (Round to the nearest hundredth if needed)- a)16 in.
- b)15 in.
- c)23.32 in.
- d)8 in.
Correct answer is option 'A'. Can you explain this answer?
A right triangle has a side with length 12 in and a hypotenuse with length 20 in. Find the length of the second leg. (Round to the nearest hundredth if needed)
a)
16 in.
b)
15 in.
c)
23.32 in.
d)
8 in.
|
|
Ritu Saxena answered |
Since we are working with a right triangle, and we are missing a leg, we can use the Pythagorean Theorem to solve for that missing leg.
Pythagorean Theorem: A2 + B2 = C2
A = 1 2 B = ? C = 20
122 + B2 = 202 Substitute
144 + B2 = 400 Simplify
144 - 144 + B2 = 400 - 144
Subtract 144 from both sides.
B2 = 256 Simplify
Take the square root of both sides.
B = 16
Pythagorean Theorem: A2 + B2 = C2
A = 1 2 B = ? C = 20
122 + B2 = 202 Substitute
144 + B2 = 400 Simplify
144 - 144 + B2 = 400 - 144
Subtract 144 from both sides.
B2 = 256 Simplify
Take the square root of both sides.
B = 16
If a, b are the roots of the equation x2 + x + 1 = 0 then a2 + b2 = ?- a)1
- b)2
- c)3
- d)-1
Correct answer is option 'D'. Can you explain this answer?
If a, b are the roots of the equation x2 + x + 1 = 0 then a2 + b2 = ?
a)
1
b)
2
c)
3
d)
-1
|
|
Samiksha dasgupta answered |
To find the value of a² - b², we need to first determine the values of a and b.
Given that a and b are the roots of the equation x² + x + 1 = 0, we can use the quadratic formula to solve for them.
The quadratic formula states that for an equation in the form ax² + bx + c = 0, the solutions can be found using the formula:
x = (-b ± √(b² - 4ac)) / (2a)
In this case, a = 1, b = 1, and c = 1. Substituting these values into the quadratic formula, we get:
x = (-(1) ± √((1)² - 4(1)(1))) / (2(1))
= (-1 ± √(1 - 4)) / 2
= (-1 ± √(-3)) / 2
Since the discriminant (√(b² - 4ac)) is negative, we have complex roots. Let's simplify the expression:
x = (-1 ± i√3) / 2
Therefore, a = (-1 + i√3) / 2 and b = (-1 - i√3) / 2.
Now, let's substitute these values into the expression a² - b²:
a² - b² = [(-1 + i√3) / 2]² - [(-1 - i√3) / 2]²
Expanding the squares:
a² - b² = [(-1 + i√3) / 2] * [(-1 + i√3) / 2] - [(-1 - i√3) / 2] * [(-1 - i√3) / 2]
Simplifying each term:
a² - b² = [(-1 + i√3)(-1 + i√3)] / 4 - [(-1 - i√3)(-1 - i√3)] / 4
Using the distributive property:
a² - b² = (1 - i√3 - i√3 + 3) / 4 - (1 + i√3 + i√3 + 3) / 4
Combining like terms:
a² - b² = (4 - 2i√3) / 4 - (4 + 2i√3) / 4
Simplifying further:
a² - b² = (4 - 4 - 2i√3 - 2i√3) / 4
a² - b² = (-4i√3) / 4
Simplifying the fraction:
a² - b² = -i√3
Therefore, the correct answer is option D, -1.
Given that a and b are the roots of the equation x² + x + 1 = 0, we can use the quadratic formula to solve for them.
The quadratic formula states that for an equation in the form ax² + bx + c = 0, the solutions can be found using the formula:
x = (-b ± √(b² - 4ac)) / (2a)
In this case, a = 1, b = 1, and c = 1. Substituting these values into the quadratic formula, we get:
x = (-(1) ± √((1)² - 4(1)(1))) / (2(1))
= (-1 ± √(1 - 4)) / 2
= (-1 ± √(-3)) / 2
Since the discriminant (√(b² - 4ac)) is negative, we have complex roots. Let's simplify the expression:
x = (-1 ± i√3) / 2
Therefore, a = (-1 + i√3) / 2 and b = (-1 - i√3) / 2.
Now, let's substitute these values into the expression a² - b²:
a² - b² = [(-1 + i√3) / 2]² - [(-1 - i√3) / 2]²
Expanding the squares:
a² - b² = [(-1 + i√3) / 2] * [(-1 + i√3) / 2] - [(-1 - i√3) / 2] * [(-1 - i√3) / 2]
Simplifying each term:
a² - b² = [(-1 + i√3)(-1 + i√3)] / 4 - [(-1 - i√3)(-1 - i√3)] / 4
Using the distributive property:
a² - b² = (1 - i√3 - i√3 + 3) / 4 - (1 + i√3 + i√3 + 3) / 4
Combining like terms:
a² - b² = (4 - 2i√3) / 4 - (4 + 2i√3) / 4
Simplifying further:
a² - b² = (4 - 4 - 2i√3 - 2i√3) / 4
a² - b² = (-4i√3) / 4
Simplifying the fraction:
a² - b² = -i√3
Therefore, the correct answer is option D, -1.
If A and B are the roots of the quadratic equation x2 - 12x + 27 = 0, then A3 + B3 is- a)27
- b)729
- c)756
- d)64
Correct answer is option 'C'. Can you explain this answer?
If A and B are the roots of the quadratic equation x2 - 12x + 27 = 0, then A3 + B3 is
a)
27
b)
729
c)
756
d)
64
|
Roshni verma answered |
Given:
The quadratic equation is x^2 - 12x + 27 = 0
To find:
The value of A^3 + B^3
Solution:
We know that if A and B are the roots of a quadratic equation ax^2 + bx + c = 0, then the sum of the roots is given by A + B = -b/a and the product of the roots is given by AB = c/a.
So, in the given equation x^2 - 12x + 27 = 0, the sum of the roots A and B is A + B = 12 and the product of the roots A and B is AB = 27.
Now, let's find the value of (A^3 + B^3).
Step 1:
We know that (A + B)^3 = A^3 + B^3 + 3AB(A + B)
Substituting the given values, (A + B)^3 = (12)^3
Simplifying, (A + B)^3 = 1728
Step 2:
Expanding (A + B)^3, we get A^3 + 3A^2B + 3AB^2 + B^3 = 1728
Step 3:
Substituting the values of AB and simplifying, we get A^3 + B^3 + 3(27)(12) + 12(3)(27) = 1728
Simplifying further, we get A^3 + B^3 + 324 + 972 = 1728
Step 4:
Combining like terms, we get A^3 + B^3 + 1296 = 1728
Step 5:
Subtracting 1296 from both sides, we get A^3 + B^3 = 1728 - 1296
Simplifying, we get A^3 + B^3 = 432
Answer:
Therefore, the value of A^3 + B^3 is 432.
The quadratic equation is x^2 - 12x + 27 = 0
To find:
The value of A^3 + B^3
Solution:
We know that if A and B are the roots of a quadratic equation ax^2 + bx + c = 0, then the sum of the roots is given by A + B = -b/a and the product of the roots is given by AB = c/a.
So, in the given equation x^2 - 12x + 27 = 0, the sum of the roots A and B is A + B = 12 and the product of the roots A and B is AB = 27.
Now, let's find the value of (A^3 + B^3).
Step 1:
We know that (A + B)^3 = A^3 + B^3 + 3AB(A + B)
Substituting the given values, (A + B)^3 = (12)^3
Simplifying, (A + B)^3 = 1728
Step 2:
Expanding (A + B)^3, we get A^3 + 3A^2B + 3AB^2 + B^3 = 1728
Step 3:
Substituting the values of AB and simplifying, we get A^3 + B^3 + 3(27)(12) + 12(3)(27) = 1728
Simplifying further, we get A^3 + B^3 + 324 + 972 = 1728
Step 4:
Combining like terms, we get A^3 + B^3 + 1296 = 1728
Step 5:
Subtracting 1296 from both sides, we get A^3 + B^3 = 1728 - 1296
Simplifying, we get A^3 + B^3 = 432
Answer:
Therefore, the value of A^3 + B^3 is 432.
Roots of the quadratic equation x2 + x – (a + 1)(a + 2) = 0 are ________.- a)–(a + 1), (a + 2)
- b)(a + 1), –(a + 2)
- c)(a + 1), (a + 2)
- d)–(a + 1), –(a + 2)
Correct answer is option 'B'. Can you explain this answer?
Roots of the quadratic equation x2 + x – (a + 1)(a + 2) = 0 are ________.
a)
–(a + 1), (a + 2)
b)
(a + 1), –(a + 2)
c)
(a + 1), (a + 2)
d)
–(a + 1), –(a + 2)
|
|
Ritu Saxena answered |
Given equation is x2 + x – (a + 1)(a + 2) = 0
⇒ x2 + (a + 2)x – (a + 1)x – (a + 1) (a + 2) = 0
⇒ x(x + (a + 2)) – (a + 1)(x + (a + 2)) = 0
⇒ (x – (a + 1))(x + (a + 2)) = 0
⇒ x = (a + 1) or x = – (a + 2)
⇒ x2 + (a + 2)x – (a + 1)x – (a + 1) (a + 2) = 0
⇒ x(x + (a + 2)) – (a + 1)(x + (a + 2)) = 0
⇒ (x – (a + 1))(x + (a + 2)) = 0
⇒ x = (a + 1) or x = – (a + 2)
If the roots of the equation (a – b)x2 + (b – c)x + (c – a) = 0 are equal. Then _______.- a)2b = a + c
- b)2a = b + c
- c)2c = a + b
- d)
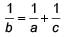
Correct answer is option 'B'. Can you explain this answer?
If the roots of the equation (a – b)x2 + (b – c)x + (c – a) = 0 are equal. Then _______.
a)
2b = a + c
b)
2a = b + c
c)
2c = a + b
d)
|
|
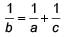
Ritu Saxena answered |
Since the given equation has equal roots.
∴ D = 0
⇒ (b – c)2 – 4(c – a) (a – b) = 0
⇒ 4a2 + b2 + c2 – 4ab + 2bc – 4ac = 0
⇒ (–2a)2 + (b)2 + (c)2 + 2(–2a)(b) + 2bc + 2(–2a)(c) = 0
⇒ (–2a + b + c)2 = 0
⇒ –2a + b + c = 0 ⇒ 2a = b + c
∴ D = 0
⇒ (b – c)2 – 4(c – a) (a – b) = 0
⇒ 4a2 + b2 + c2 – 4ab + 2bc – 4ac = 0
⇒ (–2a)2 + (b)2 + (c)2 + 2(–2a)(b) + 2bc + 2(–2a)(c) = 0
⇒ (–2a + b + c)2 = 0
⇒ –2a + b + c = 0 ⇒ 2a = b + c
If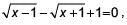 
then 4x is equal to ________.- a)
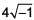
- b)0
- c)5
- d)1(1/4)
Correct answer is option 'C'. Can you explain this answer?
If 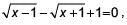then 4x is equal to ________.
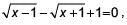then 4x is equal to ________.a)
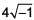
b)
0
c)
5
d)
1(1/4)
|
|
Priyanka Kapoor answered |
Given equation is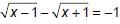 
...(1)
Rationalising (1), we get
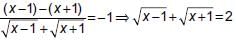...(2)
Adding (1) and (2), we get
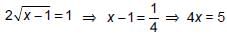
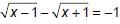...(1)Rationalising (1), we get
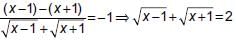...(2)Adding (1) and (2), we get
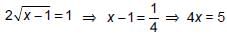
If one root of the equation x2 + px + 12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots then the value of q is- a)4/49
- b)4
- c)49/4
- d)7/4
Correct answer is option 'C'. Can you explain this answer?
If one root of the equation x2 + px + 12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots then the value of q is
a)
4/49
b)
4
c)
49/4
d)
7/4
|
|
Ritu Saxena answered |
Here x2 + px + q = 0 has one root a = 4
∴ 42 + b4 + 12 = 0
⇒ b = -7
Now the equation x2 - 7x + q = 0 has equal roots
(-7)2 - 4 (1) (q) = 0 then
⇒ 4q = 49 ⇒ q = 49/4
∴ 42 + b4 + 12 = 0
⇒ b = -7
Now the equation x2 - 7x + q = 0 has equal roots
(-7)2 - 4 (1) (q) = 0 then
⇒ 4q = 49 ⇒ q = 49/4
Find the values of y for the following equation:
2y2 - 5y + 2 = 5- a)y = − 1/2 and y = 3
- b)y = 1/2 and y = -3
- c)y = 1/2 and y = 2
- d)y = − 1/2 and y = -2
Correct answer is option 'A'. Can you explain this answer?
Find the values of y for the following equation:
2y2 - 5y + 2 = 5
2y2 - 5y + 2 = 5
a)
y = − 1/2 and y = 3
b)
y = 1/2 and y = -3
c)
y = 1/2 and y = 2
d)
y = − 1/2 and y = -2
|
|
Ritu Saxena answered |
In order to find the values for y, we must set the equation equal to 0 by subtracting 5 from both sides.
2y2 - 5y + 2 - 5 = 5 - 5
Subtract 5 from both sides
2y2 - 5y - 3 = 0
Now the equation is set equal to 0.
As I take a look at the answers, it looks like this equation can be factored. Let’s try!
(2y + 1) (y - 3) = 0 Factor the equation
2y + 1 = 0 y - 3 = 0
Set each factor equal to 0
2y + 1 - 1 = 0 - 1 y - 3 + 3 = 0 + 3
2y = -1 y = 3
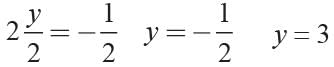
2y2 - 5y + 2 - 5 = 5 - 5
Subtract 5 from both sides
2y2 - 5y - 3 = 0
Now the equation is set equal to 0.
As I take a look at the answers, it looks like this equation can be factored. Let’s try!
(2y + 1) (y - 3) = 0 Factor the equation
2y + 1 = 0 y - 3 = 0
Set each factor equal to 0
2y + 1 - 1 = 0 - 1 y - 3 + 3 = 0 + 3
2y = -1 y = 3
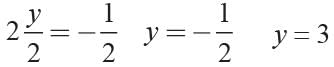
If x =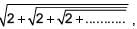 
then _______.- a)x = 1
- b)0 < x < 1
- c)x is infinite
- d)x = 2
Correct answer is option 'D'. Can you explain this answer?
If x = 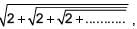then _______.
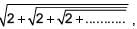then _______.a)
x = 1
b)
0 < x < 1
c)
x is infinite
d)
x = 2
|
|
Vivek Bansal answered |
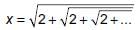...(i)Squaring both sides of (1), we get
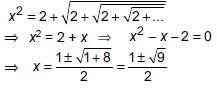
Since x cannot be negative, therefore, neglect
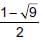
Thus, x = 2
Find the x-intercepts for the following equation.
Y = 6x2 - 7x - 3- a)(7,0) (12,0)
- b)(3,0) (-1,0)
- c)
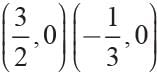
- d)
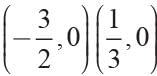
Correct answer is option 'C'. Can you explain this answer?
Find the x-intercepts for the following equation.
Y = 6x2 - 7x - 3
Y = 6x2 - 7x - 3
a)
(7,0) (12,0)
b)
(3,0) (-1,0)
c)
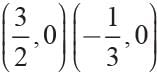
d)
|
|
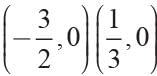
Ritu Saxena answered |
In order to find the x-intercepts, we can let y = 0 and solve for x. We can solve by possible factoring or by using the quadratic formula. Let’s use the discriminant to decide which method would be best.
0 = 6x2 - 7x - 3
where a = 6
b = -7
c = -3
Discriminate: b2 - 4ac
(-7)2 - 4(6) (-3) = 121.
This is postive and a perfect square, so let’s factor!
0 = 6x2 - 7x - 3
where a = 6
b = -7
c = -3
Discriminate: b2 - 4ac
(-7)2 - 4(6) (-3) = 121.
This is postive and a perfect square, so let’s factor!
If -5, is a root of the quadratic equation 2x2 + Px - 15 = 0 and the quadratic equation P (x2 +x) + K = 0 has equal roots. What is the value of K?- a)7/4
- b)7/8
- c)4/7
- d)8/7
Correct answer is option 'A'. Can you explain this answer?
If -5, is a root of the quadratic equation 2x2 + Px - 15 = 0 and the quadratic equation P (x2 +x) + K = 0 has equal roots. What is the value of K?
a)
7/4
b)
7/8
c)
4/7
d)
8/7
|
|
Ritu Saxena answered |
The given equation is
2x2 + Px - 15 = 0
2(-5)2 + P(-5) - 15 = 0
⇒ 50 - 5P - 15 = 0
⇒ -5P = - 35
⇒ P = 7
P(x2 + x) + K = 0
⇒ 7(x2 + x) + K = 0 ⇒ 7x2 + 7x + K = 0
⇒ a = 7, b = 7, c = K
∴ D = b2 - 4ac = (7)2 - 4(7)K = 49 - 28K
The equation has equal roots
D = 0 ⇒ 49 - 28K = 0 ⇒ K = 49/28 = 7/4
2x2 + Px - 15 = 0
2(-5)2 + P(-5) - 15 = 0
⇒ 50 - 5P - 15 = 0
⇒ -5P = - 35
⇒ P = 7
P(x2 + x) + K = 0
⇒ 7(x2 + x) + K = 0 ⇒ 7x2 + 7x + K = 0
⇒ a = 7, b = 7, c = K
∴ D = b2 - 4ac = (7)2 - 4(7)K = 49 - 28K
The equation has equal roots
D = 0 ⇒ 49 - 28K = 0 ⇒ K = 49/28 = 7/4
Which statement best describes the solutions to the equation below?
3x2 - 5x + 20 = 0- a)There are 2 rational solutions
- b)There are 2 irrational solutions
- c)There are no real solutions
- d)There is one rational solution
Correct answer is option 'C'. Can you explain this answer?
Which statement best describes the solutions to the equation below?
3x2 - 5x + 20 = 0
3x2 - 5x + 20 = 0
a)
There are 2 rational solutions
b)
There are 2 irrational solutions
c)
There are no real solutions
d)
There is one rational solution
|
|
Ritu Saxena answered |
In order to determine which statement best represents this equation, I would need to find the discriminate. Discriminate: b2 - 4ac
where: a = 3 b = -5 c = 20
(-5)2 - 4(3) (20) = -215
Since the discriminate is negative, this means that there are no real solutions.
where: a = 3 b = -5 c = 20
(-5)2 - 4(3) (20) = -215
Since the discriminate is negative, this means that there are no real solutions.
If α , β are the roots of the equation x2 - p (x + 1) - c = 0 then (α + 1) (β + 1) is equal to- a)1 + c
- b)1 - c
- c)c - 1
- d)c
Correct answer is option 'B'. Can you explain this answer?
If α , β are the roots of the equation x2 - p (x + 1) - c = 0 then (α + 1) (β + 1) is equal to
a)
1 + c
b)
1 - c
c)
c - 1
d)
c
|
|
Ritu Saxena answered |
The given equation is
x2 - p(x + 1) - c = 0
⇒ x2 - px + (-c - p) = 0
∴ α + β = p
and
Now (α + 1) (β+ 1) = αβ + α + β + 1 = - c -p + p + 1 = 1 - c
x2 - p(x + 1) - c = 0
⇒ x2 - px + (-c - p) = 0
∴ α + β = p
and
Now (α + 1) (β+ 1) = αβ + α + β + 1 = - c -p + p + 1 = 1 - c
Find the value of x. (Be sure to give all solutions)
x2 - 6 = 138- a)11.49
- b)12
- c)±12
- d)72
Correct answer is option 'C'. Can you explain this answer?
Find the value of x. (Be sure to give all solutions)
x2 - 6 = 138
x2 - 6 = 138
a)
11.49
b)
12
c)
±12
d)
72
|
|
Priyanka Kapoor answered |
Simplifying x2 + -6 = 138
Reorder the terms: -6 + x2 = 138
Solving -6 + x2 = 138
Solving for variable 'x'
Move all terms containing x to the left, all other terms to the right
Add '6' to each side of the equation
-6 + 6 + x2 = 138 + 6
Combine like terms: -6 + 6 = 0
0 + x2 = 138 + 6
x2 = 138 + 6
Combine like terms: 138 + 6 = 144
x2 = 144
Simplifying x2 = 144
Take the square root of each side:
x = {-12, 12}
Reorder the terms: -6 + x2 = 138
Solving -6 + x2 = 138
Solving for variable 'x'
Move all terms containing x to the left, all other terms to the right
Add '6' to each side of the equation
-6 + 6 + x2 = 138 + 6
Combine like terms: -6 + 6 = 0
0 + x2 = 138 + 6
x2 = 138 + 6
Combine like terms: 138 + 6 = 144
x2 = 144
Simplifying x2 = 144
Take the square root of each side:
x = {-12, 12}
If one root of the equation a ( b – c ) x2 + b(c – a)x + c(a – b) = 0 is 1, then the other root is ___.- a)
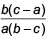
- b)
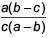
- c)
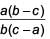
- d)
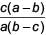
Correct answer is option 'D'. Can you explain this answer?
If one root of the equation a ( b – c ) x2 + b(c – a)x + c(a – b) = 0 is 1, then the other root is ___.
a)
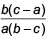
b)
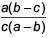
c)
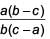
d)
|
|
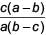
Vivek Bansal answered |
Given equation is a(b – c)x2 + b(c – a)x + c(a – b) = 0
Let α be the other root, then
Product of roots =
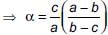
Let α be the other root, then
Product of roots =
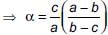
The roots of a quadratic equation are 7 and -3, then what is the equation?- a)x2 + 10x - 21 = 0
- b)x2 - 4x - 21 = 0
- c)x2 - 4x + 21 = 0
- d)x2 - 7x + 21 = 0
Correct answer is option 'B'. Can you explain this answer?
The roots of a quadratic equation are 7 and -3, then what is the equation?
a)
x2 + 10x - 21 = 0
b)
x2 - 4x - 21 = 0
c)
x2 - 4x + 21 = 0
d)
x2 - 7x + 21 = 0
|
|
Ritu Saxena answered |
The required equation is
x2 - (Sum of roots)x + Product of roots = 0
⇒ x2 - [7 + (- 3)]x + (7) (- 3) = 0
⇒ x2 - 4x - 21 = 0
x2 - (Sum of roots)x + Product of roots = 0
⇒ x2 - [7 + (- 3)]x + (7) (- 3) = 0
⇒ x2 - 4x - 21 = 0
If a < 0, then function f(x) = ax2 + bx + c has a maximum value at- a)
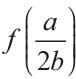
- b)
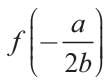
- c)
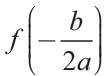
- d)None of Above
Correct answer is option 'C'. Can you explain this answer?
If a < 0, then function f(x) = ax2 + bx + c has a maximum value at
a)
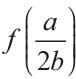
b)
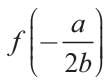
c)
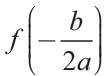
d)
None of Above
|
|
Vivek Bansal answered |
The graph of a quadratic equation is parabola.
If a < 0, then the parabola opens downward. If the parabola opens downward, then the vertex is the point whose y-value is the maximum value of f.
If a < 0, then the parabola opens downward. If the parabola opens downward, then the vertex is the point whose y-value is the maximum value of f.
In the equation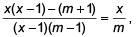 
the roots are equal when m = ________.- a)1/2
- b)-(1/2)
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
In the equation 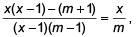the roots are equal when m = ________.
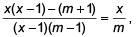the roots are equal when m = ________.a)
1/2
b)
-(1/2)
c)
0
d)
1
|
|
Vivek Bansal answered |
We have,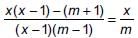 
⇒ (x2 – x)m – (m2 + m) = x(x – 1)(m – 1)
⇒ x2m – mx – m2 – m = x2m – x2 – xm + x
⇒ (x2 – m2) – (m + x) = 0
⇒ (x + m)(x – m – 1) = 0
Now, since roots are equal ⇒ –m = m + 1 ⇒ m = (-1)/2
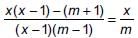
⇒ (x2 – x)m – (m2 + m) = x(x – 1)(m – 1)
⇒ x2m – mx – m2 – m = x2m – x2 – xm + x
⇒ (x2 – m2) – (m + x) = 0
⇒ (x + m)(x – m – 1) = 0
Now, since roots are equal ⇒ –m = m + 1 ⇒ m = (-1)/2
The roots of the equation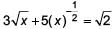 
can be found by solving ________. - a)9x2 + 28x + 25 = 0
- b)9x2 + 30x + 25 = 0
- c)9x2 + 28x – 25 = 0
- d)16x2 + 22x – 30 = 0
Correct answer is option 'A'. Can you explain this answer?
The roots of the equation 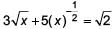can be found by solving ________.
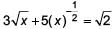can be found by solving ________. a)
9x2 + 28x + 25 = 0
b)
9x2 + 30x + 25 = 0
c)
9x2 + 28x – 25 = 0
d)
16x2 + 22x – 30 = 0
|
|
Priyanka Kapoor answered |
We have, 3x1/2 + 5x−1/2 = √2
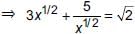
⇒ 3x + 5 = (2x)1/2 ...(1)
Squaring both sides of (1), we have
9x2 + 25 + 30x = 2x
⇒ 9x2 + 28x + 25 = 0
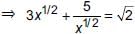
⇒ 3x + 5 = (2x)1/2 ...(1)
Squaring both sides of (1), we have
9x2 + 25 + 30x = 2x
⇒ 9x2 + 28x + 25 = 0
For what value of a, the roots of t he equation 2x2 + 6x + a = 0, satisfy the condition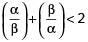 
(where α and β are the roots of equation). - a)a < 0
- b)–1 < a < 0
- c)–1 < a < 1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
For what value of a, the roots of t he equation 2x2 + 6x + a = 0, satisfy the condition 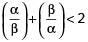(where α and β are the roots of equation).
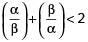(where α and β are the roots of equation). a)
a < 0
b)
–1 < a < 0
c)
–1 < a < 1
d)
None of these
|
|
Ritu Saxena answered |
Given equation is 2x2 + 6x + a = 0
Now,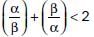
⇒
⇒
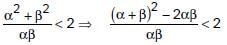
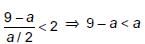
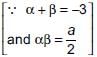
⇒ (9/2) < a
Now,
⇒
⇒
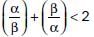
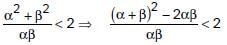
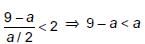
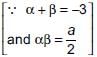
⇒ (9/2) < a
Graph of quadratic function is- a)Circle
- b)Parabola
- c)Triangle
- d)Rectangle
Correct answer is option 'B'. Can you explain this answer?
Graph of quadratic function is
a)
Circle
b)
Parabola
c)
Triangle
d)
Rectangle
|
|
Priyanka Kapoor answered |
The graph of a quadratic function is called a parabola.
Chapter doubts & questions for Quadratic Equations - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadratic Equations - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Olympiad Preparation for Class 10
70 videos|242 docs|187 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup