All Exams >
Grade 9 >
Calculus AB >
All Questions
All questions of Unit 7: Differential Equations for Grade 9 Exam
The solution of the initial value problem edy/dx = x + 1, y(0) = 3 is :
- a)y = (x – 1)log(x + 1) + 3
- b)y = (x + 1)log(x + 1) -x+3
- c)y = (x + 1)log(x + 1) + 4
- d)y = (x + 1)log(x + 1) – 1
Correct answer is option 'B'. Can you explain this answer?
The solution of the initial value problem edy/dx = x + 1, y(0) = 3 is :
a)
y = (x – 1)log(x + 1) + 3
b)
y = (x + 1)log(x + 1) -x+3
c)
y = (x + 1)log(x + 1) + 4
d)
y = (x + 1)log(x + 1) – 1
|
|
Preeti Iyer answered |
edy/dx = x + 1
⇒ dy/dx = log(x+1)
⇒ dy = log(x+1)dx
Integrating both sides, we get
⇒ ∫dy = ∫log(x+1)dx
y = log(x + 1) ∫1dx - ∫[d/dx{log(x + 1)} ∫1dx]dx
y = xlog(x + 1) - ∫1/(x+1)xdx
y = xlog(x + 1) - ∫(1 - 1/(x + 1)dx
y = xlog(x + 1) - ∫dx + ∫1/(x+1)dx
y = xlog(x + 1) - x + log|x + 1| + c
y = (x + 1)log|x + 1| - x + c
Here c is 3
y = (x + 1)log|x + 1| - x + 3
⇒ dy/dx = log(x+1)
⇒ dy = log(x+1)dx
Integrating both sides, we get
⇒ ∫dy = ∫log(x+1)dx
y = log(x + 1) ∫1dx - ∫[d/dx{log(x + 1)} ∫1dx]dx
y = xlog(x + 1) - ∫1/(x+1)xdx
y = xlog(x + 1) - ∫(1 - 1/(x + 1)dx
y = xlog(x + 1) - ∫dx + ∫1/(x+1)dx
y = xlog(x + 1) - x + log|x + 1| + c
y = (x + 1)log|x + 1| - x + c
Here c is 3
y = (x + 1)log|x + 1| - x + 3
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The differential equation, is a:
is a:
- a)second order, third degree equation.
- b)second order, second degree equation.
- c)third order, third degree equation.
- d)second order, first degree equation
Correct answer is option 'D'. Can you explain this answer?
The differential equation, is a:
is a:
a)
second order, third degree equation.
b)
second order, second degree equation.
c)
third order, third degree equation.
d)
second order, first degree equation

|
Aashu answered |
I assume you know the basics of order and degree.. And i am going to tell only why degree is 2... Since a polynomial must have power as natural no. Not a fraction... So we square both side and then expand.. You will find power of highest order(d^2y/dx^2) is 2... It is called degree.. So degree is 2
Low Haemoglobin causes________.
- a)Malaria
- b)Anaemia
- c)Cancer
- d)Cholera
Correct answer is option 'B'. Can you explain this answer?
Low Haemoglobin causes________.
a)
Malaria
b)
Anaemia
c)
Cancer
d)
Cholera
|
|
Priyanka Sharma answered |
Hemoglobin, the substance that gives color to red blood cells, is the substance that allows for the transport of oxygen throughout the body. Low hemoglobin levels lead to anemia, which causes symptoms like fatigue and trouble breathing.
The differential equation 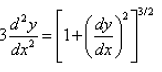 is a:
is a:- a)Third order, third degree equation
- b)Second order, second degree equation
- c)Second order, first degree equation
- d)Second order, third degree equation
Correct answer is option 'B'. Can you explain this answer?
The differential equation 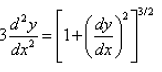 is a:
is a:
a)
Third order, third degree equation
b)
Second order, second degree equation
c)
Second order, first degree equation
d)
Second order, third degree equation
|
|
Suresh Iyer answered |
3*(d2y/dx2) = [1+(dy/dx)2]3/2
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
Differential equation representing the family of curves given by y = ax + x2 is:- a)
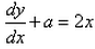
- b)

- c)

- d)
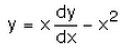
Correct answer is option 'C'. Can you explain this answer?
Differential equation representing the family of curves given by y = ax + x2 is:
a)
b)
c)
d)
|
|
Vikas Kapoor answered |
The answer is C. We eliminate constants.
We have
y=ax+x2
Differentiating with respect to x,
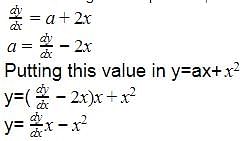
The solution of the differential equation 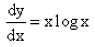 is :
is :- a)2y = x2(log x + 1) + c
- b)

- c)
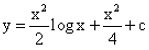
- d)y = x2(log x + 1) + c
Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation 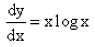 is :
is :
a)
2y = x2(log x + 1) + c
b)
c)
d)
y = x2(log x + 1) + c
|
|
Poonam Reddy answered |
dy/dx = x logx
=> ∫dy = ∫x logx dx
y = logx . x2/2 - ∫1/x . x2/2 dx + c
y = x2/2 log x -½ ∫x dx + c
y = x2/2 log x - ½ . x2/2 + c
y = x2/2 log x - x2/4 + c
=> ∫dy = ∫x logx dx
y = logx . x2/2 - ∫1/x . x2/2 dx + c
y = x2/2 log x -½ ∫x dx + c
y = x2/2 log x - ½ . x2/2 + c
y = x2/2 log x - x2/4 + c
The integrating factor of differential equation is :
is :- a)-tan x
- b)sec2x
- c)-sec2x
- d)tan x
Correct answer is option 'B'. Can you explain this answer?
The integrating factor of differential equation is :
is :
a)
-tan x
b)
sec2x
c)
-sec2x
d)
tan x
|
|
Vikas Kapoor answered |
dy/dx+2ytanx=sinx
This is in the form of dy/dx + py = θ
where p=2tanx,θ=sinx
∴ finding If e∫pdx = e∫2tanxdx
=e(2log secx)
=e(log sec2x)
=sec2x
This is in the form of dy/dx + py = θ
where p=2tanx,θ=sinx
∴ finding If e∫pdx = e∫2tanxdx
=e(2log secx)
=e(log sec2x)
=sec2x
The solution of the differential equation x dy = (2y + 2x4 + x2) dx is:- a)y = x4 + x2 log |x2 + cx2
- b)y = x3 + 2x + cx2
- c)y = x3 + x log |x| + cx
- d)y = x4 + x2 log |x| + cx2
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation x dy = (2y + 2x4 + x2) dx is:
a)
y = x4 + x2 log |x2 + cx2
b)
y = x3 + 2x + cx2
c)
y = x3 + x log |x| + cx
d)
y = x4 + x2 log |x| + cx2

|
Sai Kulkarni answered |
xdy = (2y + 2x4 + x2)dx
→ dy/dx − (2x)y = 2x3 + x
This differential is of the form y′+P(x)y=Q(x) which is the general first order linear differential equation, where P(x) and Q(x) are continuous function defined on an interval.
The general solution for this is y∙I.F = ∫I.F × Q(x)dx
Where I.F = e∫P(x)dx is the integrating factor of the differential equation.
I.F = e∫P(x)dx
= e∫−2/xdx
= e(−2∙lnx)
= eln(x−2)
= x−2
Thus y(1/x2) = ∫1/x2(2x3 + x)dx
=∫(2x + 1/x)dx
= x2 + lnx + C
⟹ y = x4 + x2lnx + c
→ dy/dx − (2x)y = 2x3 + x
This differential is of the form y′+P(x)y=Q(x) which is the general first order linear differential equation, where P(x) and Q(x) are continuous function defined on an interval.
The general solution for this is y∙I.F = ∫I.F × Q(x)dx
Where I.F = e∫P(x)dx is the integrating factor of the differential equation.
I.F = e∫P(x)dx
= e∫−2/xdx
= e(−2∙lnx)
= eln(x−2)
= x−2
Thus y(1/x2) = ∫1/x2(2x3 + x)dx
=∫(2x + 1/x)dx
= x2 + lnx + C
⟹ y = x4 + x2lnx + c
The solution of the differential equation  is :
is :
- a)a log sec by + beax = c
- b)a log (sec by + tan by) = beax + c
- c)a log (sec by + tan by) + beax = c
- d)a log sec by + beax + c
Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation  is :
is :
a)
a log sec by + beax = c
b)
a log (sec by + tan by) = beax + c
c)
a log (sec by + tan by) + beax = c
d)
a log sec by + beax + c
|
|
Aryan Khanna answered |
dy/dx = eax cos by
∫dy/cos by = ∫eax dx
∫sec by dy = ∫eax dx
= (log| sec by + tan by|)/b = eax /a + c
= a(log| sec by + tan by|) = beax + c
∫dy/cos by = ∫eax dx
∫sec by dy = ∫eax dx
= (log| sec by + tan by|)/b = eax /a + c
= a(log| sec by + tan by|) = beax + c
The number of arbitrary constants in the particular solution of a differential equation of third order are:- a)2
- b)0
- c)3
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of arbitrary constants in the particular solution of a differential equation of third order are:
a)
2
b)
0
c)
3
d)
1

|
Akshay Sharma answered |
0 , because the particular solution is free from arbitrary constants.
Order of a differential equation is defined as- a)the number of constant terms
- b)the order of the lowest order derivative ofthe dependent variable
- c)the order of the highest order derivative ofthe dependent variable
- d)the number of derivative terms
Correct answer is option 'C'. Can you explain this answer?
Order of a differential equation is defined as
a)
the number of constant terms
b)
the order of the lowest order derivative ofthe dependent variable
c)
the order of the highest order derivative ofthe dependent variable
d)
the number of derivative terms

|
Sagarika Ahuja answered |
Order of a differential equation is defined asthe order of the highest order derivative ofthe dependent variable.
The solution of the differential equation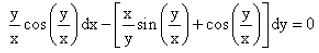 is :
is :- a)

- b)
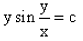
- c)
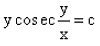
- d)

Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation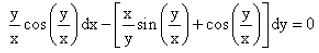 is :
is :
a)
b)
c)
d)
|
|
Aryan Khanna answered |
y/x cos y/x dx − (x/y sin y/x + cosy/x) dy = 0
⇒dy/dx = (y/x cos y/x)/(x/y sin y/x + cos y/x)
This is a homogeneous differential equation.
Putting y = vx and dy/dx = v+xdv/dx, we have v+xdv/dx = (v2cosv)/(sinv+vcosv)
⇒ xdv/dx = (v2cosv)/(sinv+vcosv) - v
⇒x dv/dx = (v2 cosv - v2 cosv - vsinv )/(sinv+vcosv)
⇒ x dv/dx = - [v sinv/(sinv + vcosv)]
⇒ ∫[(sinv + vcosv)/v sinv]dv = ∫dx/x
Integrating both the sides, we get
∫(cot v + 1/v)dv = - ln(x) + c
ln(sin v) + ln(v) = -ln(x) + c
ln(sin(y/x) + ln(y/x) + ln(x) = c
ln(y/x sin y/x * x) + c
y sin(y/x) = c
⇒dy/dx = (y/x cos y/x)/(x/y sin y/x + cos y/x)
This is a homogeneous differential equation.
Putting y = vx and dy/dx = v+xdv/dx, we have v+xdv/dx = (v2cosv)/(sinv+vcosv)
⇒ xdv/dx = (v2cosv)/(sinv+vcosv) - v
⇒x dv/dx = (v2 cosv - v2 cosv - vsinv )/(sinv+vcosv)
⇒ x dv/dx = - [v sinv/(sinv + vcosv)]
⇒ ∫[(sinv + vcosv)/v sinv]dv = ∫dx/x
Integrating both the sides, we get
∫(cot v + 1/v)dv = - ln(x) + c
ln(sin v) + ln(v) = -ln(x) + c
ln(sin(y/x) + ln(y/x) + ln(x) = c
ln(y/x sin y/x * x) + c
y sin(y/x) = c
The solution of the equation x3dx + (y + 1)2 dy = 0- a)12[x4 - (y +1)3] = c
- b)12[x4 + (y +1)3] = c
- c)3x4 + 4(y +1)3 = c
- d)3x4 + 3(y +1)3 = c
Correct answer is option 'C'. Can you explain this answer?
The solution of the equation x3dx + (y + 1)2 dy = 0
a)
12[x4 - (y +1)3] = c
b)
12[x4 + (y +1)3] = c
c)
3x4 + 4(y +1)3 = c
d)
3x4 + 3(y +1)3 = c
|
|
Om Desai answered |
x3dx + (y + 1)dy = 0
=> d(x4/4) + d((y + 1)3/3) = 0
=> d(x4/4 + ((y + 1)3/3)) = 0
=> (x4/4 + ((y + 1)3/3)) = constt
=> 12 *(x4/4 + ((y + 1)3/3)) = 12 * constt
=> 3x4 + 4(y + 1)3 = constt
=> d(x4/4) + d((y + 1)3/3) = 0
=> d(x4/4 + ((y + 1)3/3)) = 0
=> (x4/4 + ((y + 1)3/3)) = constt
=> 12 *(x4/4 + ((y + 1)3/3)) = 12 * constt
=> 3x4 + 4(y + 1)3 = constt
The solution of the differential equation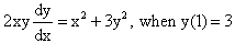 is :
is :- a)x3 + 10y3 = x2
- b)x3 + y3 = 10x2
- c)x3 + y2 = 10x3
- d)x3 -10y3 = x2
Correct answer is option 'C'. Can you explain this answer?
The solution of the differential equation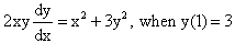 is :
is :
a)
x3 + 10y3 = x2
b)
x3 + y3 = 10x2
c)
x3 + y2 = 10x3
d)
x3 -10y3 = x2
|
|
Om Desai answered |
dy/dx = (x2 + 3y2)/2xy………….(1)
Let y = vx
dy/dx = v + xdv/dx
Substitute the value of y and dy/dx in (1)
v + x dv/dx = (1+3v2)/2v
x dv/dx = (1+3v2)/2v - v
x dv/dx = (1 + 3v2 - 2v2)/2
x dv/dx = (1+ v2)/2v
2v/(1+v2) dv = dx/x…………(2)
Integrating both the sides
∫2v/(1+v2) dv = ∫dx/x
Put t = 1 + v2
dt = 2vdv
∫dt/t = ∫dx/x
=> log|t| = log|x| + log|c|
=> log|t/x| = log|c|
t/x = +- c
(1+v2)/x = +-c
(1 + (y2)/(x2))/x = +-c
x2 + y2 = Cx3……….(3)
y(1) = 3
1 + 9 = c(1)3
c = 10
From eq(3), we get x
Let y = vx
dy/dx = v + xdv/dx
Substitute the value of y and dy/dx in (1)
v + x dv/dx = (1+3v2)/2v
x dv/dx = (1+3v2)/2v - v
x dv/dx = (1 + 3v2 - 2v2)/2
x dv/dx = (1+ v2)/2v
2v/(1+v2) dv = dx/x…………(2)
Integrating both the sides
∫2v/(1+v2) dv = ∫dx/x
Put t = 1 + v2
dt = 2vdv
∫dt/t = ∫dx/x
=> log|t| = log|x| + log|c|
=> log|t/x| = log|c|
t/x = +- c
(1+v2)/x = +-c
(1 + (y2)/(x2))/x = +-c
x2 + y2 = Cx3……….(3)
y(1) = 3
1 + 9 = c(1)3
c = 10
From eq(3), we get x
3
+ y2 = 10x3The solution of the differential equation is :
is :- a)

- b)

- c)

- d)
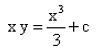
Correct answer is option 'A'. Can you explain this answer?
The solution of the differential equation is :
is :
a)
b)
c)
d)

|
Notes Wala answered |
dy/dx + y/x = x2
differential equation is in the form : dy/dx + Py = Q
P = 1/x Q = x2
I.F = e∫P(x)dx
I.F = e∫1/x dx
I.F = e[log x]
I.F = x
y I.F = ∫(Q * I.F) dx + c
yx = ∫x2 * x * dx + c
yx = ∫x3 dx + c
xy = [x4]/4 + c
differential equation is in the form : dy/dx + Py = Q
P = 1/x Q = x2
I.F = e∫P(x)dx
I.F = e∫1/x dx
I.F = e[log x]
I.F = x
y I.F = ∫(Q * I.F) dx + c
yx = ∫x2 * x * dx + c
yx = ∫x3 dx + c
xy = [x4]/4 + c
The solution of the differential equation is :
is :- a)
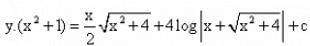
- b)

- c)

- d)
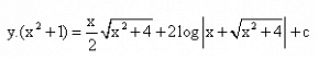
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation is :
is :
a)
b)
c)
d)
|
|
Om Desai answered |
The given differential equation may be written as
dy/dx + (2x/(x2+1)y = √x2+4/(x2+1) ... (i)
This is of the form dy/dx + Py = Q,
where P=2x/(x2+1) and Q=(√x2+4)/(x2+1)
Thus, the given differential equation is linear.
IF=e(∫Pdx)
= e(∫2x(x2+1)dx)
= e(log(x2+1) = (x2+1)
So, the required solution is given by
y × IF = ∫{Q×IF}dx + C,
i.e., y(x2+1)=∫(√x2+4)/(x2+1)×(x2+1)dx
⇒y(x2+1)=∫(√x2+4)dx
=1/2x (√x2+4) +1/2 × (2)2 × log|x+(√x2+4)| + C
=1/2x (√x2+4) + 2log|x+(√x2+4) + C.
Hence, y(x2+1) = 1/2x(√x2+4) + 2log|x+√x2+4| + C is the required solution.
dy/dx + (2x/(x2+1)y = √x2+4/(x2+1) ... (i)
This is of the form dy/dx + Py = Q,
where P=2x/(x2+1) and Q=(√x2+4)/(x2+1)
Thus, the given differential equation is linear.
IF=e(∫Pdx)
= e(∫2x(x2+1)dx)
= e(log(x2+1) = (x2+1)
So, the required solution is given by
y × IF = ∫{Q×IF}dx + C,
i.e., y(x2+1)=∫(√x2+4)/(x2+1)×(x2+1)dx
⇒y(x2+1)=∫(√x2+4)dx
=1/2x (√x2+4) +1/2 × (2)2 × log|x+(√x2+4)| + C
=1/2x (√x2+4) + 2log|x+(√x2+4) + C.
Hence, y(x2+1) = 1/2x(√x2+4) + 2log|x+√x2+4| + C is the required solution.
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :- a)
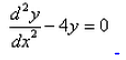
- b)

- c)

- d)
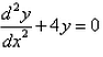
Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :
a)
b)
c)
d)
|
|
Toushit Lohani answered |
Diiferentiate the eqn twice
y' =2(Ae^2x-Be^2x)
y''=4(Ae^2x+Be^2x)
we get
y''-4y=0
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:- a)
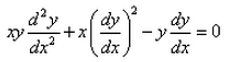
- b)
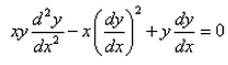
- c)
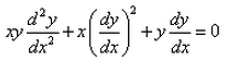
- d)

Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:
a)
b)
c)
d)
|
|
Geetika Shah answered |
Equation of ellipse :
x2/a2 + y2/b2 = 1
Differentiation by x,
2x/a2 + (dy/dx)*(2y/b2) = 0
dy/dx = -(b2/a2)(x/y)
-(b2/a^2) = (dy/dx)*(y/x) ----- eqn 1
Again differentiating by x,
d2y/dx2 = -(b2/a2)*((y-x(dy/dx))/y2)
Substituting value of -b2/a2 from eqn 1
d2y/dx2 = (dy/dx)*(y/x)*((y-x(dy/dx))/y2)
d2y/dx2 = (dy/dx)*((y-x*(dy/dx))/xy)
(xy)*(d2y/dx2) = y*(dy/dx) - x*(dy/dx)2
(xy)*(d2y/dx2) + x*(dy/dx)2- y*(dy/dx) = 0
The first order, first degree differential equation y’ = f(x,y) is said to be homogeneous, if- a)f(x , y) is a homogeneous function of degree zero.
- b)f(x , y) is a homogeneous function of second degree.
- c)f(x , y) is a homogeneous function of first degree.
- d)f(x , y) is a homogeneous function of third degree.
Correct answer is option 'A'. Can you explain this answer?
The first order, first degree differential equation y’ = f(x,y) is said to be homogeneous, if
a)
f(x , y) is a homogeneous function of degree zero.
b)
f(x , y) is a homogeneous function of second degree.
c)
f(x , y) is a homogeneous function of first degree.
d)
f(x , y) is a homogeneous function of third degree.

|
Arshiya Mehta answered |
The correct answer is option A, because a first-order, first-degree differential equation is said to be homogeneous if the function f(x,y) is a homogeneous function of degree zero.
A function f(x,y) is said to be homogeneous of degree n if it satisfies the equation:
f(λx, λy) = λ^n * f(x,y)
where λ is a scalar. This means that if we multiply both the independent and dependent variables by a constant λ, the value of the function is scaled by a factor of λ^n.
In the case of a first-order, first-degree differential equation, the function f(x,y) is a function of two variables: x and y. For this type of equation, f(x,y) is said to be homogeneous if it is a homogeneous function of degree zero, which means that it satisfies the equation:
f(λx, λy) = f(x,y)
In other words, if we multiply both the independent and dependent variables by a constant λ, the value of the function does not change. This means that f(x,y) does not depend on the magnitude of the variables x and y, but only on their relative values.
For example, if f(x,y) = xy, then f(λx, λy) = λxy = xy, so f(x,y) is a homogeneous function of degree zero. On the other hand, if f(x,y) = x^2 + y^2, then f(λx, λy) = λ^2x^2 + λ^2y^2 = x^2 + y^2, so f(x,y) is not a homogeneous function.
Therefore, the correct answer is option A, because a first-order, first-degree differential equation is said to be homogeneous if the function f(x,y) is a homogeneous function of degree zero.
Identify the type of differential equation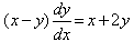
- a)Variable separable
- b)Homogeneous
- c)Linear
- d)Both Variable separable and Linear
Correct answer is option 'B'. Can you explain this answer?
Identify the type of differential equation
a)
Variable separable
b)
Homogeneous
c)
Linear
d)
Both Variable separable and Linear
|
|
Tejas Verma answered |
(x−y)dy/dx = x + 2y
⇒ dy/dx = (x + 2y)/(x−y)
F (x,y) = (x + 2y)/(x−y)
F(Ax, Ay) = (Ax + 2Ay)/(Ax−Ay)
= A(x + 2y)/A(x−y)
= (x + 2y)/(x − y) = F (x,y)
Hence, the equation is homogenous.
⇒ dy/dx = (x + 2y)/(x−y)
F (x,y) = (x + 2y)/(x−y)
F(Ax, Ay) = (Ax + 2Ay)/(Ax−Ay)
= A(x + 2y)/A(x−y)
= (x + 2y)/(x − y) = F (x,y)
Hence, the equation is homogenous.
Write the order and degree of the given differential equation:
- a)2,3
- b)1,1
- c)2,1
- d)3, 1
Correct answer is option 'D'. Can you explain this answer?
Write the order and degree of the given differential equation:
a)
2,3
b)
1,1
c)
2,1
d)
3, 1
|
|
Gaurav Kumar answered |
Order = 3 and Degree = 1
The order of a differential equation is determined by the highest-order derivative; the degree is determined by the highest power on a variable. The higher the order of the differential equation, the more arbitrary constants need to be added to the general solution.
The order of a differential equation is determined by the highest-order derivative; the degree is determined by the highest power on a variable. The higher the order of the differential equation, the more arbitrary constants need to be added to the general solution.
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).- a)7.93%
- b)8.93%
- c)9.93%
- d)6.93%
Correct answer is option 'D'. Can you explain this answer?
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
a)
7.93%
b)
8.93%
c)
9.93%
d)
6.93%
|
|
Anirban Desai answered |
To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial amount)
r is the annual interest rate (as a decimal)
n is the number of times the interest is compounded per year
t is the number of years
In this case, the principal doubles itself in 10 years. So, the final amount A is 2 times the principal P.
2P = P(1 + r/n)^(nt)
Since we are given that the principal increases continuously, we can take the limit as n approaches infinity. This simplifies the formula to:
2 = e^(rt)
Where e is the base of natural logarithms and is approximately equal to 2.71828.
Now, we can take the natural logarithm of both sides to solve for r:
ln(2) = rt
Dividing both sides by t:
r = ln(2)/t
Given that t = 10 years, we can substitute this value into the equation:
r = ln(2)/10
Using the given value of loge2 = 0.6931, we can calculate r:
r = 0.6931/10 = 0.06931 = 6.93%
Therefore, the value of r is 6.93%.
So, the correct answer is option D.
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial amount)
r is the annual interest rate (as a decimal)
n is the number of times the interest is compounded per year
t is the number of years
In this case, the principal doubles itself in 10 years. So, the final amount A is 2 times the principal P.
2P = P(1 + r/n)^(nt)
Since we are given that the principal increases continuously, we can take the limit as n approaches infinity. This simplifies the formula to:
2 = e^(rt)
Where e is the base of natural logarithms and is approximately equal to 2.71828.
Now, we can take the natural logarithm of both sides to solve for r:
ln(2) = rt
Dividing both sides by t:
r = ln(2)/t
Given that t = 10 years, we can substitute this value into the equation:
r = ln(2)/10
Using the given value of loge2 = 0.6931, we can calculate r:
r = 0.6931/10 = 0.06931 = 6.93%
Therefore, the value of r is 6.93%.
So, the correct answer is option D.
Degree of a differential equation, when the equation is polynomial equation in y′ is- a)Highest (positive integral index) of the lowest order derivative in the given differential equation.
- b)Lowest power (positive integral index) of the highest order derivative in the given differential equation.
- c)Lowest power (positive integral index) of the lowest order derivative in the given differential equation.
- d)Highest power (positive integral index) of the highest order derivative in the given differential equation.
Correct answer is option 'D'. Can you explain this answer?
Degree of a differential equation, when the equation is polynomial equation in y′ is
a)
Highest (positive integral index) of the lowest order derivative in the given differential equation.
b)
Lowest power (positive integral index) of the highest order derivative in the given differential equation.
c)
Lowest power (positive integral index) of the lowest order derivative in the given differential equation.
d)
Highest power (positive integral index) of the highest order derivative in the given differential equation.
|
|
Malavika Menon answered |
The degree of a differential equation is determined by the highest power of the derivative(s) present in the equation.
When the equation is a polynomial equation in y, the degree is determined by the highest power of y in the equation. The derivative(s) of y do not affect the degree in this case.
When the equation is a polynomial equation in y, the degree is determined by the highest power of y in the equation. The derivative(s) of y do not affect the degree in this case.
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:- a)2, 4
- b)3, 5
- c)2, 5
- d)2, 3
Correct answer is option 'D'. Can you explain this answer?
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:
a)
2, 4
b)
3, 5
c)
2, 5
d)
2, 3
|
|
Naina Bansal answered |
Toolbox:
The highest order derivative present in the differential equation determines its order.
The highest power raise to the derivative determines its degree.
(y′′′)^2+(y′′)^3+(y′)^4+y^5 = 0
The order of the given equation is 3.
The degree corresponding to the highest order is 2
The solution of the differential equation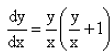 is :
is :- a)

- b)
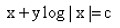
- c)
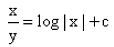
- d)
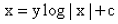
Correct answer is option 'A'. Can you explain this answer?
The solution of the differential equation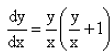 is :
is :
a)
b)
c)
d)

|
Peter Parker answered |
Option A is correct...
Find the differential equation of all the straight lines touching the circle x2 + y2 = r2.
- a)r2 (1+(dy/dx))2
- b)3r2 (1+(dx/dy))2
- c)2r2 (1+(dy/dx))2
- d)r2 (1+(dx/dy))2
Correct answer is option 'A'. Can you explain this answer?
Find the differential equation of all the straight lines touching the circle x2 + y2 = r2.
a)
r2 (1+(dy/dx))2
b)
3r2 (1+(dx/dy))2
c)
2r2 (1+(dy/dx))2
d)
r2 (1+(dx/dy))2
|
|
Ajay Yadav answered |
- Let y = mx + c be the equation of all the straight lines touching the circle.Given : The equation of the circle is x2 + y2 = r2----------> (1)The tangent to the circle is c2 = r2(1+m2)c = r√(1+m2)we know that y = mx + c---------->(2)y = mx + r√(1+m2) ---------->(3)y - mx = r√(1+m2)Differentiating wrt x we get dy/dx -m =0dy/dx = mSubstituting this in equation (3)y - (dy/dx . x) = r√(1+(dy/dx)2)Squaring on both sides, we gety2 - (dy/dx . x)2 = [ r√(1+(dy/dx)2)]2[y - x(dy/dx)]2 = r2 (1+(dy/dx))2 is the required differential equation.Answer: The differential equation of all the straight lines touching the circle x2 + y2 = r2 is [y - x(dy/dx)]2 = r2 (1+(dy/dx))2

Differential equations are equations containing functions y = f(x), g(x) and- a)tangent of y at zero
- b)maxima of y
- c)derivatives of y
- d)minima of y
Correct answer is option 'C'. Can you explain this answer?
Differential equations are equations containing functions y = f(x), g(x) and
a)
tangent of y at zero
b)
maxima of y
c)
derivatives of y
d)
minima of y
|
|
Dipanjan Verma answered |
Differential equations are mathematical equations that involve derivatives of an unknown function. They are widely used in various fields of science and engineering to model and analyze dynamic systems. In this question, we are asked to identify the correct option regarding the nature of the functions involved in differential equations.
Differential equations involve functions y = f(x) and g(x), where y represents the dependent variable and x represents the independent variable. These functions can have various properties and behaviors based on the given equation. Let's analyze each option to understand why option 'C' is the correct answer.
a) Tangent of y at zero:
The tangent of a function at a specific point represents the slope of the function at that point. This option suggests that the differential equation involves the tangent of y at zero. However, this is not a general characteristic of differential equations. Differential equations can involve tangents at any point, not just zero.
b) Maxima of y:
Maxima of a function refers to the points where the function reaches its highest values. While differential equations can involve maxima or minima, it is not a general property of all differential equations. Therefore, this option is not correct.
c) Derivatives of y:
This option suggests that the differential equations involve derivatives of y. This is the correct answer. Differential equations often involve derivatives of the unknown function y with respect to the independent variable x. By including derivatives, we can describe how the rate of change of y varies with respect to x.
d) Minima of y:
Minima of a function refers to the points where the function reaches its lowest values. Similar to option 'b', this is not a general property of all differential equations. While some differential equations may involve minima, it is not a defining characteristic.
In conclusion, the correct answer is option 'c' because differential equations commonly involve derivatives of the unknown function y. Including derivatives allows us to describe the rate of change and behavior of the function with respect to the independent variable.
Differential equations involve functions y = f(x) and g(x), where y represents the dependent variable and x represents the independent variable. These functions can have various properties and behaviors based on the given equation. Let's analyze each option to understand why option 'C' is the correct answer.
a) Tangent of y at zero:
The tangent of a function at a specific point represents the slope of the function at that point. This option suggests that the differential equation involves the tangent of y at zero. However, this is not a general characteristic of differential equations. Differential equations can involve tangents at any point, not just zero.
b) Maxima of y:
Maxima of a function refers to the points where the function reaches its highest values. While differential equations can involve maxima or minima, it is not a general property of all differential equations. Therefore, this option is not correct.
c) Derivatives of y:
This option suggests that the differential equations involve derivatives of y. This is the correct answer. Differential equations often involve derivatives of the unknown function y with respect to the independent variable x. By including derivatives, we can describe how the rate of change of y varies with respect to x.
d) Minima of y:
Minima of a function refers to the points where the function reaches its lowest values. Similar to option 'b', this is not a general property of all differential equations. While some differential equations may involve minima, it is not a defining characteristic.
In conclusion, the correct answer is option 'c' because differential equations commonly involve derivatives of the unknown function y. Including derivatives allows us to describe the rate of change and behavior of the function with respect to the independent variable.
General solution of a given differential equation- a)contains arbitrary constants depending on the order of the differential equation
- b)contains exactly one arbitrary constant
- c)contains exactly two arbitrary constants
- d)does not contain arbitrary constants
Correct answer is option 'A'. Can you explain this answer?
General solution of a given differential equation
a)
contains arbitrary constants depending on the order of the differential equation
b)
contains exactly one arbitrary constant
c)
contains exactly two arbitrary constants
d)
does not contain arbitrary constants
|
|
Madhurima Mehta answered |
The general solution of a given differential equation contains arbitrary constants depending on the order of the differential equation. Let's understand this in detail:
1. Differential Equation:
A differential equation is an equation that relates a function with its derivatives. It represents a relationship between the function and its rate of change.
2. Order of a Differential Equation:
The order of a differential equation is the highest order of the derivative present in the equation. For example, if the equation involves only the first derivative of the function, it is a first-order differential equation. Similarly, if it involves the second derivative, it is a second-order differential equation, and so on.
3. Particular Solution:
A particular solution is a specific solution of a differential equation that satisfies the given initial conditions.
4. General Solution:
The general solution of a differential equation is a family of solutions that contains all possible solutions of the equation. It includes a set of functions that satisfy the differential equation, along with arbitrary constants.
5. Arbitrary Constants:
Arbitrary constants are constants that can take any value. They are introduced in the general solution to account for the different solutions that satisfy the given differential equation.
6. Number of Arbitrary Constants:
The number of arbitrary constants in the general solution depends on the order of the differential equation.
- For a first-order differential equation, the general solution contains exactly one arbitrary constant.
- For a second-order differential equation, the general solution contains exactly two arbitrary constants.
- For higher-order differential equations, the general solution contains arbitrary constants equal to the order of the differential equation.
7. Importance of Arbitrary Constants:
The arbitrary constants in the general solution allow us to find the particular solution by substituting specific values for the constants. These values are determined by the given initial conditions or boundary conditions.
In conclusion, the general solution of a given differential equation contains arbitrary constants depending on the order of the differential equation. These arbitrary constants allow us to find particular solutions that satisfy the given initial or boundary conditions.
1. Differential Equation:
A differential equation is an equation that relates a function with its derivatives. It represents a relationship between the function and its rate of change.
2. Order of a Differential Equation:
The order of a differential equation is the highest order of the derivative present in the equation. For example, if the equation involves only the first derivative of the function, it is a first-order differential equation. Similarly, if it involves the second derivative, it is a second-order differential equation, and so on.
3. Particular Solution:
A particular solution is a specific solution of a differential equation that satisfies the given initial conditions.
4. General Solution:
The general solution of a differential equation is a family of solutions that contains all possible solutions of the equation. It includes a set of functions that satisfy the differential equation, along with arbitrary constants.
5. Arbitrary Constants:
Arbitrary constants are constants that can take any value. They are introduced in the general solution to account for the different solutions that satisfy the given differential equation.
6. Number of Arbitrary Constants:
The number of arbitrary constants in the general solution depends on the order of the differential equation.
- For a first-order differential equation, the general solution contains exactly one arbitrary constant.
- For a second-order differential equation, the general solution contains exactly two arbitrary constants.
- For higher-order differential equations, the general solution contains arbitrary constants equal to the order of the differential equation.
7. Importance of Arbitrary Constants:
The arbitrary constants in the general solution allow us to find the particular solution by substituting specific values for the constants. These values are determined by the given initial conditions or boundary conditions.
In conclusion, the general solution of a given differential equation contains arbitrary constants depending on the order of the differential equation. These arbitrary constants allow us to find particular solutions that satisfy the given initial or boundary conditions.
General Solution of (ex + e-x) dy - (ex - e-x) dx = 0- a)y = log(e2x+ e−x) + C
- b)y = log(ex+ e−x) + C
- c)y = (ex+ e−x) + C
- d)y = log(e−2x+ e−x) + C
Correct answer is option 'B'. Can you explain this answer?
General Solution of (ex + e-x) dy - (ex - e-x) dx = 0
a)
y = log(e2x+ e−x) + C
b)
y = log(ex+ e−x) + C
c)
y = (ex+ e−x) + C
d)
y = log(e−2x+ e−x) + C
|
|
Samridhi Deshpande answered |
General Solution of the given differential equation:
- To find the general solution of the given differential equation, start by rearranging the equation in the form of dy/dx.
- The given differential equation is: (ex+ e-x) dy - (ex- e-x) dx = 0
- Rearranging the equation gives: dy/dx = (ex- e-x) / (ex+ e-x)
Integrating the equation:
- To solve this differential equation, separate the variables and integrate both sides.
- Integrate the left side with respect to y and the right side with respect to x.
- Integrate (ex+ e-x) dy = Integrate (ex- e-x) dx
Applying Integration:
- The integral of (ex+ e-x) dy is y = log|ex+e-x| + C1, where C1 is the constant of integration.
- The integral of (ex- e-x) dx is x = log|ex-e-x| + C2, where C2 is the constant of integration.
General Solution:
- Combining the results from the integrations, the general solution of the given differential equation is:
- y = log(ex+e-x) + C1
- This is the general solution for the given differential equation.
- To find the general solution of the given differential equation, start by rearranging the equation in the form of dy/dx.
- The given differential equation is: (ex+ e-x) dy - (ex- e-x) dx = 0
- Rearranging the equation gives: dy/dx = (ex- e-x) / (ex+ e-x)
Integrating the equation:
- To solve this differential equation, separate the variables and integrate both sides.
- Integrate the left side with respect to y and the right side with respect to x.
- Integrate (ex+ e-x) dy = Integrate (ex- e-x) dx
Applying Integration:
- The integral of (ex+ e-x) dy is y = log|ex+e-x| + C1, where C1 is the constant of integration.
- The integral of (ex- e-x) dx is x = log|ex-e-x| + C2, where C2 is the constant of integration.
General Solution:
- Combining the results from the integrations, the general solution of the given differential equation is:
- y = log(ex+e-x) + C1
- This is the general solution for the given differential equation.
The order of the differential equation: 
- a)4
- b)2
- c)3
- d)1
Correct answer is option 'C'. Can you explain this answer?
The order of the differential equation: 
a)
4
b)
2
c)
3
d)
1

|
Anuj Seth answered |
Order is seen from highest efficiency of differentiability I.e. in hindi , kisi bhi equation me jisme sabse jyada differential power hai wo jeeta
Differential equation of the family of ellipses having foci on y-axis and centre at origin is- a)xy′′ + x(y′)2 yy′ = 0
- b)xyy′′ + x(y′)2 yy′ = 0
- c)yy′′ + x(y′)2 yy′ = 0
- d)xyy′′ −x(y′)2 +yy′ = 0
Correct answer is option 'B'. Can you explain this answer?
Differential equation of the family of ellipses having foci on y-axis and centre at origin is
a)
xy′′ + x(y′)2 yy′ = 0
b)
xyy′′ + x(y′)2 yy′ = 0
c)
yy′′ + x(y′)2 yy′ = 0
d)
xyy′′ −x(y′)2 +yy′ = 0
|
|
Palak Banerjee answered |
The differential equation of the family of ellipses having foci on the y-axis and center at the origin can be found as follows:
Let's consider an ellipse with foci (0, c) and (0, -c), where c is a positive constant. The distance between the foci is 2c.
The general equation of an ellipse centered at the origin is given by:
x^2/a^2 + y^2/b^2 = 1,
where a and b are positive constants representing the semi-major and semi-minor axes, respectively.
Since the foci lie on the y-axis, the equation of the ellipse becomes:
x^2/a^2 + (y - c)^2/b^2 = 1.
We know that the distance between the foci is 2c, so we have:
2c = 2b^2/a.
Simplifying this equation, we get:
b^2 = ac.
Now, differentiating both sides of the equation with respect to x, we have:
2b(b') = a'c + ac',
where b' and a' represent the derivatives of b and a with respect to x, respectively.
Since the derivatives of a and b are unknown, we cannot solve for the differential equation in terms of x and y directly. However, we can eliminate a' and b' by using the relationship b^2 = ac, which gives:
2b(b') = 2b(c'/b) + ac'.
Simplifying this equation, we find:
b' = c'/b + ac'/(2b^2).
Rearranging terms, we get:
b'(2b^2) = c' + ac'.
Substituting b^2 = ac, we obtain:
b'(2b^2) = c' + b^2c'.
Finally, dividing both sides by 2b^2, we get the differential equation:
b' = (c' + b^2c')/(2b^2).
Therefore, the differential equation of the family of ellipses having foci on the y-axis and center at the origin is:
b' = (c' + b^2c')/(2b^2).
Let's consider an ellipse with foci (0, c) and (0, -c), where c is a positive constant. The distance between the foci is 2c.
The general equation of an ellipse centered at the origin is given by:
x^2/a^2 + y^2/b^2 = 1,
where a and b are positive constants representing the semi-major and semi-minor axes, respectively.
Since the foci lie on the y-axis, the equation of the ellipse becomes:
x^2/a^2 + (y - c)^2/b^2 = 1.
We know that the distance between the foci is 2c, so we have:
2c = 2b^2/a.
Simplifying this equation, we get:
b^2 = ac.
Now, differentiating both sides of the equation with respect to x, we have:
2b(b') = a'c + ac',
where b' and a' represent the derivatives of b and a with respect to x, respectively.
Since the derivatives of a and b are unknown, we cannot solve for the differential equation in terms of x and y directly. However, we can eliminate a' and b' by using the relationship b^2 = ac, which gives:
2b(b') = 2b(c'/b) + ac'.
Simplifying this equation, we find:
b' = c'/b + ac'/(2b^2).
Rearranging terms, we get:
b'(2b^2) = c' + ac'.
Substituting b^2 = ac, we obtain:
b'(2b^2) = c' + b^2c'.
Finally, dividing both sides by 2b^2, we get the differential equation:
b' = (c' + b^2c')/(2b^2).
Therefore, the differential equation of the family of ellipses having foci on the y-axis and center at the origin is:
b' = (c' + b^2c')/(2b^2).
The order of a differential equation representing a family of curves is same as:- a)The number of arbitrary constants present in the equation.
- b)The number of variables in the equation
- c)The degree of the equation
- d)The number of curves in the family
Correct answer is option 'A'. Can you explain this answer?
The order of a differential equation representing a family of curves is same as:
a)
The number of arbitrary constants present in the equation.
b)
The number of variables in the equation
c)
The degree of the equation
d)
The number of curves in the family
|
|
Anand Kumar answered |
Once go through it definition u will find it
Solution of x dy− ydx = 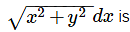
- a)

- b)
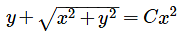
- c)

- d)
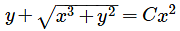
Correct answer is option 'B'. Can you explain this answer?
Solution of x dy− ydx = 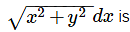
a)
b)
c)
d)
|
|
Harsh Singhal answered |
Solve by put x=rcos$ & y=rsin$
Which of the following is a homogeneous differential equation?- a)(xy) dx − (x3+ y3) dy = 0
- b)(x3+ 2y2) dx + 2xy dy = 0
- c)y2dx + (x2− xy − y2) dy = 0
- d)(4x + 6y + 5) dy − (3y + 2x + 4) dx = 0
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a homogeneous differential equation?
a)
(xy) dx − (x3+ y3) dy = 0
b)
(x3+ 2y2) dx + 2xy dy = 0
c)
y2dx + (x2− xy − y2) dy = 0
d)
(4x + 6y + 5) dy − (3y + 2x + 4) dx = 0

|
Sarthak Khanna answered |
y2dx + (x2− xy − y2) dy = 0 is a homogeneous differential equation ,because the degree of each individual term is same i.e. 2.
To form a differential equation from a given function- a)Differentiate thefunction successively as many times as the number of arbitrary constants inthe given function and eliminate the arbitrary constants.
- b)Differentiate thefunction twice and eliminate the arbitrary constants
- c)Differentiate thefunction once and eliminate the arbitrary constants
- d)Differentiate thefunction once and add values to arbitrary constants
Correct answer is option 'A'. Can you explain this answer?
To form a differential equation from a given function
a)
Differentiate thefunction successively as many times as the number of arbitrary constants inthe given function and eliminate the arbitrary constants.
b)
Differentiate thefunction twice and eliminate the arbitrary constants
c)
Differentiate thefunction once and eliminate the arbitrary constants
d)
Differentiate thefunction once and add values to arbitrary constants

|
Sagarika Ahuja answered |
To form a differential equation from a given functionDifferentiate thefunction successively as many times as the number of arbitrary constants inthe given function and eliminate the arbitrary constants.i.e. the differential equation should be free from arbitrary constants.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).- a)(x + 3)2 = y + 4
- b)(x + 5)2 = 2y + 3
- c)(x + 4)2 = y + 3
- d)(x + 5)2 = 2y + 3
Correct answer is option 'C'. Can you explain this answer?
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).
a)
(x + 3)2 = y + 4
b)
(x + 5)2 = 2y + 3
c)
(x + 4)2 = y + 3
d)
(x + 5)2 = 2y + 3

|
Ipsita Sen answered |
Slope of the line segment joining the point of contact P (x , y) to the point (- 4 , - 3) = 

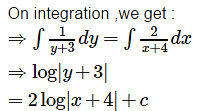

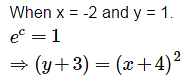
In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs1000 is deposited with this bank, how much will it worth after 10 years (e0.5= 1.648).- a)Rs 1848
- b)Rs 1648
- c)Rs 1948
- d)Rs 1748
Correct answer is option 'B'. Can you explain this answer?
In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs1000 is deposited with this bank, how much will it worth after 10 years (e0.5= 1.648).
a)
Rs 1848
b)
Rs 1648
c)
Rs 1948
d)
Rs 1748

|
Prasenjit Malik answered |


When P = 1000 and t = 0 ., then ,
c = 1000, therefore, we have :
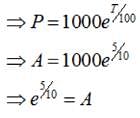

Chapter doubts & questions for Unit 7: Differential Equations - Calculus AB 2024 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Unit 7: Differential Equations - Calculus AB in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Calculus AB
22 videos|44 docs|34 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup