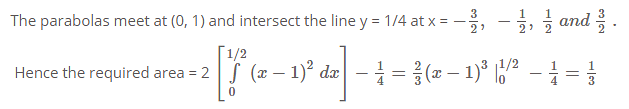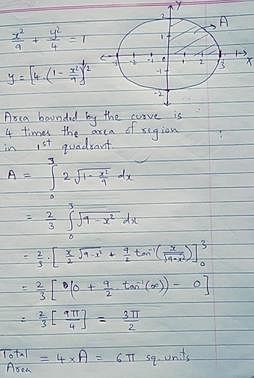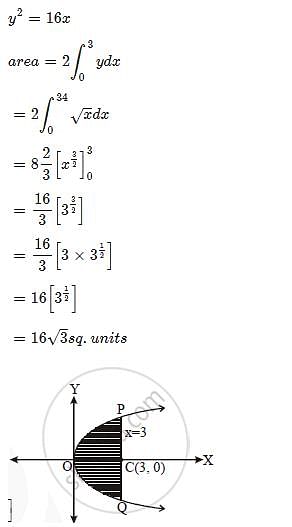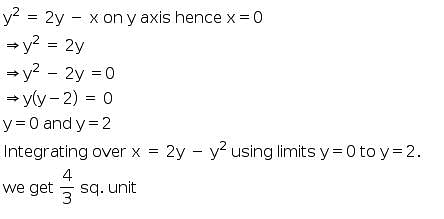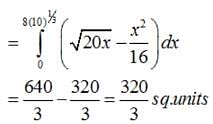All Exams >
Grade 9 >
Calculus AB >
All Questions
All questions of Unit 8: Applications of Integration for Grade 9 Exam
The area shaded in the given figure can be calculated by which of the following definite integral?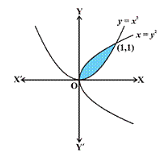
- a)

- b)
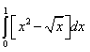
- c)
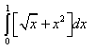
- d)
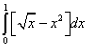
Correct answer is option 'D'. Can you explain this answer?
The area shaded in the given figure can be calculated by which of the following definite integral?
a)
b)
c)
d)
|
|
Leelu Bhai answered |
The required area is calculated by the difference ... moreof area of upper curve and lower curve.Now equation of upper curve
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The area of the region bounded by y = x2 – 2x and y = 4 – x2 is.- a)7 sq. units
- b)8 sq. units
- c)9 sq. units
- d)10 sq. units
Correct answer is option 'C'. Can you explain this answer?
The area of the region bounded by y = x2 – 2x and y = 4 – x2 is.
a)
7 sq. units
b)
8 sq. units
c)
9 sq. units
d)
10 sq. units
|
|
Vikas Kapoor answered |
To find area between y = x2 – 2x and y = 4 – x2,
We need to find POI.
x2 – 2x = 4 – x2
2x2 - 2x – 4 = 0
x2 – x – 2 = 0
(x-2)(x+1) = 0
x = -1, 2
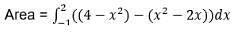

= [(-2x3)/3 + x2 + 4x]x=2 - [(-2x3)/3 + x2 + 4x]x= -1
= -16/3 + 4 + 8 – (2/3 + 1 - 4)
= 9 sq units
We need to find POI.
x2 – 2x = 4 – x2
2x2 - 2x – 4 = 0
x2 – x – 2 = 0
(x-2)(x+1) = 0
x = -1, 2
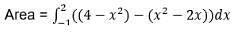

= [(-2x3)/3 + x2 + 4x]x=2 - [(-2x3)/3 + x2 + 4x]x= -1
= -16/3 + 4 + 8 – (2/3 + 1 - 4)
= 9 sq units
The area enclosed between the lines x = 2 and x = 7 is- a)Infinite
- b)7 units
- c)5 units
- d)2 units
Correct answer is option 'A'. Can you explain this answer?
The area enclosed between the lines x = 2 and x = 7 is
a)
Infinite
b)
7 units
c)
5 units
d)
2 units
|
|
Manas Khantal answered |
See from graph of x=2 & x=7 it's simple
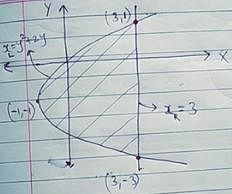
The area bounded by the curve y2 = 16x , x = 1, y = 3 and X-axis is: - a)
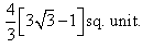
- b)

- c)
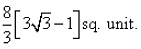
- d)
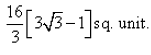
Correct answer is option 'C'. Can you explain this answer?
The area bounded by the curve y2 = 16x , x = 1, y = 3 and X-axis is:
a)
b)
c)
d)

|
Moksh Sharma answered |
Plese give detailed solution of this question
The area between the curves y = x2 and y = x3 is:
- a) 1/12 sq.units
- b) 1/8 sq.units
- c) 1/10 sq.unit
- d) 1/6 sq.units
Correct answer is option 'A'. Can you explain this answer?
The area between the curves y = x2 and y = x3 is:
a)
1/12 sq.unitsb)
1/8 sq.unitsc)
1/10 sq.unitd)
1/6 sq.units|
|
Arun Khanna answered |
First we note that the curves intersect at the points (0,0) and (1,1). Then we see that
x^3 < x^2
in this interval. Hence the area is given by
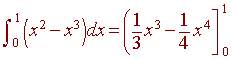
= 1/3 - 1/4 = 1/12.
The area enclosed between the curves y = √x , x = 2y+3and the x-axis is- a)9
- b)18
- c)27
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area enclosed between the curves y = √x , x = 2y+3and the x-axis is
a)
9
b)
18
c)
27
d)
none of these

|
Manisha Mehta answered |
The two curves meet where;

Therefore, the two curves meet where x = 9.
Therefore,required Area:
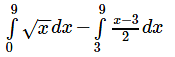

Therefore, the two curves meet where x = 9.
Therefore,required Area:
The area bounded by the curve y = 2x - x2 and the line x + y = 0 is- a)9/2 sq. units
- b)35/6 sq. units
- c)19/6 sq. units
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the curve y = 2x - x2 and the line x + y = 0 is
a)
9/2 sq. units
b)
35/6 sq. units
c)
19/6 sq. units
d)
none of these

|
Pranav Pillai answered |
The equation y = 2x − x2 i.e. y – 1 = - (x - 1)2 represents a downward parabola with vertex at (1, 1) which meets x – axis where y = 0 .i .e . where x = 0 , 2. Also , the line y = - x meets this parabola where – x = 2x − x2 i.e. where x = 0 , 3.
Therefore , required area is :
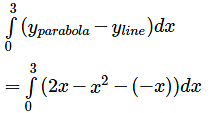
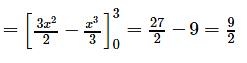
Therefore , required area is :
The area bounded by the angle bisectors of the lines x2−y2+2y = 1 and x+y = 3 is- a)6 sq. units
- b)2 sq. units
- c)3 sq.units
- d)4 sq. units
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the angle bisectors of the lines x2−y2+2y = 1 and x+y = 3 is
a)
6 sq. units
b)
2 sq. units
c)
3 sq.units
d)
4 sq. units

|
Jatin Dasgupta answered |
The angle bisectors of the line given by x2−− y2+2y = 1 are x = 0 , y = 1. Required area = 1/2 .2.2 = 2 sq. units
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to- a)12 sq. units
- b)6 sq. units
- c)9 sq. units
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to
a)
12 sq. units
b)
6 sq. units
c)
9 sq. units
d)
none of these

|
Mohit Patel answered |
Therefore, tangent at (2, 3) is y – 3 = ½ (x – 2). i.e. x – 2y +4 = 0 . therefore required area is
Area of the region bounded by the curves y = ex, x = a , x = b and the x- axis is given by- a)eb−ea
- b)eb−a
- c)eb+ea
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Area of the region bounded by the curves y = ex, x = a , x = b and the x- axis is given by
a)
eb−ea
b)
eb−a
c)
eb+ea
d)
none of these
|
|
Nisha Sen answered |
To find the area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis, we can use integration.
Step 1: Determine the limits of integration
The region is bounded by the vertical lines x = a and x = b, so the limits of integration for x will be from a to b.
Step 2: Set up the integral
The area of the region can be found by integrating the function y = ex with respect to x over the given limits of integration.
The integral for the area is given by:
∫(ex) dx from a to b
Step 3: Evaluate the integral
Integrating the function ex with respect to x gives us ex.
So, the integral becomes:
∫(ex) dx = ex
Evaluating this integral from a to b gives us:
ex evaluated from a to b = eb - ea
Step 4: Subtracting the areas below the x-axis
Since the region is bounded by the x-axis, we need to consider the areas below the x-axis as negative.
If there are any values of x within the interval (a, b) where ex is negative, we need to subtract the absolute value of the integral of ex in that range. However, since the function ex is always positive, we don't need to consider this step.
Step 5: Finalize the answer
The area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis is given by:
Area = eb - ea
Therefore, the correct answer is option A) eb - ea.
Step 1: Determine the limits of integration
The region is bounded by the vertical lines x = a and x = b, so the limits of integration for x will be from a to b.
Step 2: Set up the integral
The area of the region can be found by integrating the function y = ex with respect to x over the given limits of integration.
The integral for the area is given by:
∫(ex) dx from a to b
Step 3: Evaluate the integral
Integrating the function ex with respect to x gives us ex.
So, the integral becomes:
∫(ex) dx = ex
Evaluating this integral from a to b gives us:
ex evaluated from a to b = eb - ea
Step 4: Subtracting the areas below the x-axis
Since the region is bounded by the x-axis, we need to consider the areas below the x-axis as negative.
If there are any values of x within the interval (a, b) where ex is negative, we need to subtract the absolute value of the integral of ex in that range. However, since the function ex is always positive, we don't need to consider this step.
Step 5: Finalize the answer
The area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis is given by:
Area = eb - ea
Therefore, the correct answer is option A) eb - ea.
The area bounded by the parabolas y = 5x2and y − 9 = 2x2 is- a)12√3 sq.units
- b)6√2 sq.units
- c)12√2 sq.units
- d)4√3 sq.units
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the parabolas y = 5x2and y − 9 = 2x2 is
a)
12√3 sq.units
b)
6√2 sq.units
c)
12√2 sq.units
d)
4√3 sq.units
|
|
Saranya Choudhary answered |
Explanation:
Finding the Points of Intersection:
To find the points of intersection of the two parabolas, set them equal to each other:
5x^2 = 9 - 2x^2
7x^2 = 9
x^2 = 9/7
x = ±√(9/7)
Calculating the Area Between the Curves:
Integrate the difference of the two equations between the points of intersection to find the area:
∫(9 - 2x^2) - 5x^2 dx from -√(9/7) to √(9/7)
= ∫(9 - 7x^2) dx from -√(9/7) to √(9/7)
= [9x - (7x^3)/3] from -√(9/7) to √(9/7)
Substitute the Values:
= [9√(9/7) - (7(9/7)^(3/2))/3] - [-9√(9/7) - (7(9/7)^(3/2))/3]
= (27/√7 - 21√7/3) - (-27/√7 - 21√7/3)
= 54/√7
Final Calculation:
To find the area, square the result:
(54/√7)^2 = 2916/7 = 123 sq. units
Therefore, the area bounded by the parabolas y = 5x^2 and y = 9 - 2x^2 is 123 sq. units.
Finding the Points of Intersection:
To find the points of intersection of the two parabolas, set them equal to each other:
5x^2 = 9 - 2x^2
7x^2 = 9
x^2 = 9/7
x = ±√(9/7)
Calculating the Area Between the Curves:
Integrate the difference of the two equations between the points of intersection to find the area:
∫(9 - 2x^2) - 5x^2 dx from -√(9/7) to √(9/7)
= ∫(9 - 7x^2) dx from -√(9/7) to √(9/7)
= [9x - (7x^3)/3] from -√(9/7) to √(9/7)
Substitute the Values:
= [9√(9/7) - (7(9/7)^(3/2))/3] - [-9√(9/7) - (7(9/7)^(3/2))/3]
= (27/√7 - 21√7/3) - (-27/√7 - 21√7/3)
= 54/√7
Final Calculation:
To find the area, square the result:
(54/√7)^2 = 2916/7 = 123 sq. units
Therefore, the area bounded by the parabolas y = 5x^2 and y = 9 - 2x^2 is 123 sq. units.
Let y be the function which passes through (1 , 2) having slope (2x + 1) . The area bounded between the curve and the x – axis is- a)1/6 sq. units
- b)6 sq. units
- c)5/6 sq. units
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Let y be the function which passes through (1 , 2) having slope (2x + 1) . The area bounded between the curve and the x – axis is
a)
1/6 sq. units
b)
6 sq. units
c)
5/6 sq. units
d)
none of these

|
Rhea Joshi answered |
Given slope of the curve is 2x + 1.
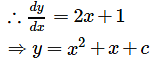
Also , it passes through (1, 2).
∴ 2 = 1+1+c ⇒ c = 0
Equation of curve is : y = x2 + x. Therefore , points of intersection of y = x (x +1) and the x – axis are x = 0 , x = - 1.
Required area :

Also , it passes through (1, 2).
∴ 2 = 1+1+c ⇒ c = 0
Equation of curve is : y = x2 + x. Therefore , points of intersection of y = x (x +1) and the x – axis are x = 0 , x = - 1.
Required area :
The area bounded by y = 2cosx , x = 0 to x = 2π and the axis of x in square units is- a)6
- b)4
- c)8
- d)7
Correct answer is option 'C'. Can you explain this answer?
The area bounded by y = 2cosx , x = 0 to x = 2π and the axis of x in square units is
a)
6
b)
4
c)
8
d)
7

|
Manisha Mehta answered |
Required area :
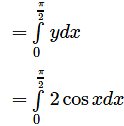

Therefore , total area from x = 0 to x = 2π is 4 X 2= 8 sq. units.
Therefore , total area from x = 0 to x = 2π is 4 X 2= 8 sq. units.
Area under the circle x2 + y2 = 16 is- a)π sq units
- b)13π sq units
- c)16 π sq units
- d)4 π sq units
Correct answer is option 'C'. Can you explain this answer?
Area under the circle x2 + y2 = 16 is
a)
π sq units
b)
13π sq units
c)
16 π sq units
d)
4 π sq units
|
|
Partho Sengupta answered |
Finding the Area under a Circle
Given the equation of the circle x^2 + y^2 = 16, we need to find the area under the circle.
Solution:
- Rewrite the equation of the circle in terms of y:
y^2 = 16 - x^2
- Take the square root of both sides:
y = ± √(16 - x^2)
- We are only concerned with the positive square root since we are finding the area under the circle, which is above the x-axis.
- Plot the graph of y = √(16 - x^2) from x = -4 to x = 4 (the limits of the circle) to see the shape of the area we are finding.
- We notice that the area under the curve is a quarter of a circle with radius 4.
- The area of a quarter circle with radius r is (πr^2)/4.
- Substituting r = 4, we get:
Area = (π(4)^2)/4 = 16π/4 = 4π
- The exact value of π is irrational, but we can approximate it to 3.14.
- So, the area under the circle is approximately:
Area ≈ 4(3.14) = 12.56
- However, the question asks for the exact area, which is:
Area = 4π = 12.57 sq units
Therefore, the correct option is "C" - 16 sq units.
Given the equation of the circle x^2 + y^2 = 16, we need to find the area under the circle.
Solution:
- Rewrite the equation of the circle in terms of y:
y^2 = 16 - x^2
- Take the square root of both sides:
y = ± √(16 - x^2)
- We are only concerned with the positive square root since we are finding the area under the circle, which is above the x-axis.
- Plot the graph of y = √(16 - x^2) from x = -4 to x = 4 (the limits of the circle) to see the shape of the area we are finding.
- We notice that the area under the curve is a quarter of a circle with radius 4.
- The area of a quarter circle with radius r is (πr^2)/4.
- Substituting r = 4, we get:
Area = (π(4)^2)/4 = 16π/4 = 4π
- The exact value of π is irrational, but we can approximate it to 3.14.
- So, the area under the circle is approximately:
Area ≈ 4(3.14) = 12.56
- However, the question asks for the exact area, which is:
Area = 4π = 12.57 sq units
Therefore, the correct option is "C" - 16 sq units.
The area bounded by the curves y2 = x and y = x2 is- a)1/2 sq. units
- b)2/3 sq. units
- c)1 sq. units
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The area bounded by the curves y2 = x and y = x2 is
a)
1/2 sq. units
b)
2/3 sq. units
c)
1 sq. units
d)
none of these

|
Nilesh Goyal answered |
The two curves meet in (0 , 0) and (1, 1).The required area lies above the curve y = x2 and below x = y2 and is equal to ;

The area bounded by the curves y2 = 4x and y = x is equal to- a)8/3
- b)35/6
- c)1/3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the curves y2 = 4x and y = x is equal to
a)
8/3
b)
35/6
c)
1/3
d)
none of these

|
Pranav Pillai answered |
The two curves y2 = 4x and y = x meet where x2 = 4x i.e ..where x = 0 or x = 4 . Moreover , the parabola lies above the line y = x between x = 0 and x = 4 . Hence , the required are is :
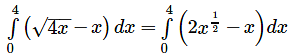
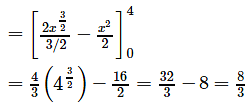

- a)π ab
- b)
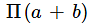
- c)

- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
π ab
b)
c)
d)
None of these

|
Mohit Patel answered |
Area of standard ellipse is given by :πab.
The area bounded by the curve y = 4x - x2 and the x- axis is equal to- a)
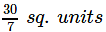
- b)
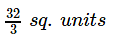
- c)
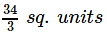
- d)
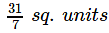
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the curve y = 4x - x2 and the x- axis is equal to
a)
b)
c)
d)

|
Rhea Joshi answered |
For x - axis, y = 0,
Therefore, 4x - x2 = 0
Therefore, x = 0 or x = 4
Required area :
Chapter doubts & questions for Unit 8: Applications of Integration - Calculus AB 2024 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Unit 8: Applications of Integration - Calculus AB in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Calculus AB
22 videos|44 docs|34 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup