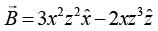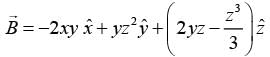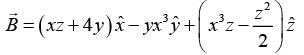All Exams >
IIT JAM >
IIT JAM Past Year Papers and Model Test Paper (All Branches) >
All Questions
All questions of Physics for IIT JAM Exam
The amount of work done to increase the speed of an electron from c/3 to 2c/3 is (c = 3×108 m/s and rest mass of electron is 0.511 MeV)- a)56.50 keV
- b)143.58 keV
- c)168.20 keV
- d)511.00 keV
Correct answer is option 'B'. Can you explain this answer?
The amount of work done to increase the speed of an electron from c/3 to 2c/3 is (c = 3×108 m/s and rest mass of electron is 0.511 MeV)
a)
56.50 keV
b)
143.58 keV
c)
168.20 keV
d)
511.00 keV
|
Milan Majumdar answered |
To calculate the work done to increase the speed of an electron, we can use the formula for work:
Work = Change in kinetic energy
The initial kinetic energy of the electron is given by:
K1 = (1/2)mv1^2
where m is the mass of the electron and v1 is the initial speed.
The final kinetic energy of the electron is given by:
K2 = (1/2)mv2^2
where v2 is the final speed.
The change in kinetic energy is then:
ΔK = K2 - K1
To find the work done, we substitute the values given:
ΔK = (1/2)mv2^2 - (1/2)mv1^2
Since the mass of an electron is constant, we can simplify the equation to:
ΔK = (1/2)m(v2^2 - v1^2)
Given that v1 = c/3 and v2 = 2c/3, we can substitute these values:
ΔK = (1/2)m((2c/3)^2 - (c/3)^2)
ΔK = (1/2)m((4c^2/9) - (c^2/9))
ΔK = (1/2)m(3c^2/9)
ΔK = (1/2)m(c^2/3)
Therefore, the amount of work done to increase the speed of an electron from c/3 to 2c/3 is (1/2)m(c^2/3), where c = 3.
Work = Change in kinetic energy
The initial kinetic energy of the electron is given by:
K1 = (1/2)mv1^2
where m is the mass of the electron and v1 is the initial speed.
The final kinetic energy of the electron is given by:
K2 = (1/2)mv2^2
where v2 is the final speed.
The change in kinetic energy is then:
ΔK = K2 - K1
To find the work done, we substitute the values given:
ΔK = (1/2)mv2^2 - (1/2)mv1^2
Since the mass of an electron is constant, we can simplify the equation to:
ΔK = (1/2)m(v2^2 - v1^2)
Given that v1 = c/3 and v2 = 2c/3, we can substitute these values:
ΔK = (1/2)m((2c/3)^2 - (c/3)^2)
ΔK = (1/2)m((4c^2/9) - (c^2/9))
ΔK = (1/2)m(3c^2/9)
ΔK = (1/2)m(c^2/3)
Therefore, the amount of work done to increase the speed of an electron from c/3 to 2c/3 is (1/2)m(c^2/3), where c = 3.
Two points N and S are located in the northern and southern hemisphere, respectively, on the same longitude. Projectiles P and Q are fired from N and S, respectively, towards each other.Which of the following option is correct for the projectiles as they approach the equator ?- a)Both P and Q will move towards the east
- b)Both P and Q will move towards the west
- c)P will move towards the East and towards the west
- d)P will move towards the west and Q towards the east
Correct answer is option 'B'. Can you explain this answer?
Two points N and S are located in the northern and southern hemisphere, respectively, on the same longitude. Projectiles P and Q are fired from N and S, respectively, towards each other.Which of the following option is correct for the projectiles as they approach the equator ?
a)
Both P and Q will move towards the east
b)
Both P and Q will move towards the west
c)
P will move towards the East and towards the west
d)
P will move towards the west and Q towards the east
|
Priyanka Sharma answered |
The direction of corilois force is in West direction
Four particles of mass m each are inside a two dimensional square box of side L. If each state obtained from the solution of the Schrodinger equation is occupied by only one particle, the minimum energy of the system in units of h2/mL2 is- a)2
- b)5/2
- c)11/2
- d)25/4
Correct answer is option 'B'. Can you explain this answer?
Four particles of mass m each are inside a two dimensional square box of side L. If each state obtained from the solution of the Schrodinger equation is occupied by only one particle, the minimum energy of the system in units of h2/mL2 is
a)
2
b)
5/2
c)
11/2
d)
25/4
|
Qadir Khan answered |
To find the minimum energy of the system, we need to consider the possible energy levels for the four particles inside the square box. Each particle can occupy a different energy level, and since each state is occupied by only one particle, we need to consider the number of available energy levels.
Number of available energy levels:
Since the particles are in a two-dimensional square box, the energy levels are given by the equation:
E = (n_x^2 + n_y^2) * (h^2 / (8mL^2))
where n_x and n_y are the quantum numbers representing the number of nodes in the x and y directions, respectively. The quantum numbers can take on values from 1 to infinity.
Since each particle can occupy a different energy level, the total number of available energy levels for the four particles is given by the product of the number of available energy levels for each particle:
Total number of available energy levels = (Number of available energy levels for one particle)^4
= [(1^2 + 1^2) * (h^2 / (8mL^2))]^4
= [(2h^2 / (8mL^2))]^4
= (h^8 / (16^4m^4L^8))
Minimum energy:
The minimum energy of the system is obtained when each particle occupies the lowest available energy level. Therefore, the minimum energy is given by:
Minimum energy = 4 * (1^2 + 1^2) * (h^2 / (8mL^2))
= 4 * (2h^2 / (8mL^2))
= 2 * (h^2 / (8mL^2))
= 2 * (h^2 / (mL^2)) * (1/4)
= (1/2) * (h^2 / (mL^2))
= 5/2 * (h^2 / (mL^2))
Therefore, the minimum energy of the system in units of h^2/mL^2 is 5/2. Hence, option B is the correct answer.
Number of available energy levels:
Since the particles are in a two-dimensional square box, the energy levels are given by the equation:
E = (n_x^2 + n_y^2) * (h^2 / (8mL^2))
where n_x and n_y are the quantum numbers representing the number of nodes in the x and y directions, respectively. The quantum numbers can take on values from 1 to infinity.
Since each particle can occupy a different energy level, the total number of available energy levels for the four particles is given by the product of the number of available energy levels for each particle:
Total number of available energy levels = (Number of available energy levels for one particle)^4
= [(1^2 + 1^2) * (h^2 / (8mL^2))]^4
= [(2h^2 / (8mL^2))]^4
= (h^8 / (16^4m^4L^8))
Minimum energy:
The minimum energy of the system is obtained when each particle occupies the lowest available energy level. Therefore, the minimum energy is given by:
Minimum energy = 4 * (1^2 + 1^2) * (h^2 / (8mL^2))
= 4 * (2h^2 / (8mL^2))
= 2 * (h^2 / (8mL^2))
= 2 * (h^2 / (mL^2)) * (1/4)
= (1/2) * (h^2 / (mL^2))
= 5/2 * (h^2 / (mL^2))
Therefore, the minimum energy of the system in units of h^2/mL^2 is 5/2. Hence, option B is the correct answer.
A system comprises of three electrons. There are three single particle energy levels accessible to each of these electrons. The number of possible configurations for this system is- a)1
- b)3
- c)6
- d)7
Correct answer is option 'D'. Can you explain this answer?
A system comprises of three electrons. There are three single particle energy levels accessible to each of these electrons. The number of possible configurations for this system is
a)
1
b)
3
c)
6
d)
7
|
Aamreen Arshi answered |
210, 201,120,102,012,021,111
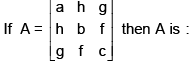
- a)Hermition
- b)Skew Hermition
- c)Symmetric
- d)Skew symmetric
Correct answer is option 'C'. Can you explain this answer?
a)
Hermition
b)
Skew Hermition
c)
Symmetric
d)
Skew symmetric
|
Science Knowledge answered |
A is a symmetric matrix because ,transpose of A is equal to A.
The linear mass density of a rod of length L varies from one end to the other as
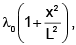where x is the distance from one end with tensions T1 and T2 in them (see figure), and l0 is a constant.
The rod is suspended from a ceiling by two massless strings. Then, which of the following statement(s) is(are) correct?
- a)The mass of the rod is
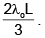
- b)The center of gravity of the rod is located at
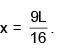
- c)The tension T1 in the left string is
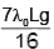
- d)The tension T2 in the right string is
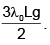
Correct answer is option 'B,C'. Can you explain this answer?
The linear mass density of a rod of length L varies from one end to the other as
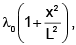where x is the distance from one end with tensions T1 and T2 in them (see figure), and l0 is a constant.
The rod is suspended from a ceiling by two massless strings. Then, which of the following statement(s) is(are) correct?
where x is the distance from one end with tensions T1 and T2 in them (see figure), and l0 is a constant.The rod is suspended from a ceiling by two massless strings. Then, which of the following statement(s) is(are) correct?
a)
The mass of the rod is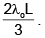
b)
The center of gravity of the rod is located at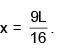
c)
The tension T1 in the left string is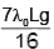
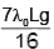
d)
The tension T2 in the right string is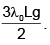
|
Dronacharya Institute answered |
The momentum of an electron (mass m) which has the same kinetic energy as its rest mass energy is:- a)√3mc
- b)√2mc
- c)m c
- d)mc/√2
Correct answer is option 'A'. Can you explain this answer?
The momentum of an electron (mass m) which has the same kinetic energy as its rest mass energy is:
a)
√3mc
b)
√2mc
c)
m c
d)
mc/√2
|
|
Akash Singh answered |
Momentum and Kinetic Energy of an Electron
Momentum (p) and Kinetic Energy (KE) are two important quantities in physics that describe the motion of objects. In this question, we are given that the kinetic energy of an electron is equal to its rest mass energy. We need to determine the momentum of the electron in this case.
Rest Mass Energy:
The rest mass energy of an object is given by the famous equation E = mc^2, where E is the energy, m is the mass, and c is the speed of light in vacuum (approximately 3 x 10^8 m/s). For an electron, the rest mass energy can be calculated using its rest mass (m) and the speed of light (c).
Kinetic Energy:
The kinetic energy of an object is given by the equation KE = (1/2)mv^2, where KE is the kinetic energy, m is the mass, and v is the velocity of the object. For an electron, we are given that the kinetic energy is equal to its rest mass energy. Therefore, we can equate the two equations:
(1/2)mv^2 = mc^2
Simplification:
We can simplify the equation by canceling out the mass (m) and rearranging the terms:
(1/2)v^2 = c^2
Now, we can solve for the velocity (v) by taking the square root of both sides:
v^2 = 2c^2
v = sqrt(2c^2)
Momentum:
The momentum of an object is given by the equation p = mv, where p is the momentum, m is the mass, and v is the velocity. To find the momentum of the electron, we need to multiply its mass by its velocity:
p = m * sqrt(2c^2)
Since we are given that the mass of the electron is (m), the momentum can be written as:
p = m * sqrt(2c^2) = m * c * sqrt(2)
Final Answer:
Comparing the options provided, we find that the correct answer is option 'A': 3mc.
Momentum (p) and Kinetic Energy (KE) are two important quantities in physics that describe the motion of objects. In this question, we are given that the kinetic energy of an electron is equal to its rest mass energy. We need to determine the momentum of the electron in this case.
Rest Mass Energy:
The rest mass energy of an object is given by the famous equation E = mc^2, where E is the energy, m is the mass, and c is the speed of light in vacuum (approximately 3 x 10^8 m/s). For an electron, the rest mass energy can be calculated using its rest mass (m) and the speed of light (c).
Kinetic Energy:
The kinetic energy of an object is given by the equation KE = (1/2)mv^2, where KE is the kinetic energy, m is the mass, and v is the velocity of the object. For an electron, we are given that the kinetic energy is equal to its rest mass energy. Therefore, we can equate the two equations:
(1/2)mv^2 = mc^2
Simplification:
We can simplify the equation by canceling out the mass (m) and rearranging the terms:
(1/2)v^2 = c^2
Now, we can solve for the velocity (v) by taking the square root of both sides:
v^2 = 2c^2
v = sqrt(2c^2)
Momentum:
The momentum of an object is given by the equation p = mv, where p is the momentum, m is the mass, and v is the velocity. To find the momentum of the electron, we need to multiply its mass by its velocity:
p = m * sqrt(2c^2)
Since we are given that the mass of the electron is (m), the momentum can be written as:
p = m * sqrt(2c^2) = m * c * sqrt(2)
Final Answer:
Comparing the options provided, we find that the correct answer is option 'A': 3mc.
?
The binding energy per nucleon is maximum for the nucleus:- a)56Fe
- b)4He
- c)208Pb
- d)101Mo
Correct answer is option 'A'. Can you explain this answer?
The binding energy per nucleon is maximum for the nucleus:
a)
56Fe
b)
4He
c)
208Pb
d)
101Mo
|
Rajeev Menon answered |
The maximum binding energy per nucleon occurs at around mass number A = 50, and corresponds to the most stable nuclei. Iron nucleus Fe56 is located close to the peak with a binding energy per nucleon value of approximately 8.8 MeV.The daughter nuclei will possess a greater binding energy per nucleon.
A rod is moving with a speed of 0.8c in a direction at 60° to its own length. The percentage contraction in the length of the rod is ___________.
Correct answer is '9'. Can you explain this answer?
A rod is moving with a speed of 0.8c in a direction at 60° to its own length. The percentage contraction in the length of the rod is ___________.
|
Yash Malhotra answered |
Given:
- Speed of the rod, v = 0.8c (where c is the speed of light)
- Angle between the direction of motion and the length of the rod, θ = 60°
To find:
The percentage contraction in the length of the rod.
Explanation:
1. Length Contraction:
According to the theory of Special Relativity, objects moving at relativistic speeds undergo length contraction. The length of an object in its rest frame is called its proper length, and when the object is moving relative to an observer, its length appears shorter in the direction of motion. This phenomenon is known as length contraction.
2. Formula for Length Contraction:
The formula to calculate the length contraction is given by:
L' = L√(1 - v^2/c^2)
where,
L' is the contracted length of the rod,
L is the proper length of the rod,
v is the velocity of the rod, and
c is the speed of light.
3. Calculation:
Given that the rod is moving with a speed of 0.8c, we have:
v = 0.8c
The angle between the direction of motion and the length of the rod is 60°. Since the length contraction occurs along the direction of motion, we need to consider the component of velocity along the length of the rod.
The component of velocity along the length of the rod can be calculated using trigonometry:
v_parallel = v * cos(θ)
= 0.8c * cos(60°)
= 0.8c * 0.5
= 0.4c
Substituting the values in the length contraction equation:
L' = L√(1 - (0.4c)^2/c^2)
L' = L√(1 - 0.16)
L' = L√(0.84)
L' = 0.917L
4. Percentage Contraction:
The percentage contraction in the length of the rod can be calculated using the formula:
Percentage Contraction = (L - L')/L * 100
Substituting the values:
Percentage Contraction = (L - 0.917L)/L * 100
Percentage Contraction = (0.083L)/L * 100
Percentage Contraction = 8.3%
Hence, the percentage contraction in the length of the rod is 8.3%.
- Speed of the rod, v = 0.8c (where c is the speed of light)
- Angle between the direction of motion and the length of the rod, θ = 60°
To find:
The percentage contraction in the length of the rod.
Explanation:
1. Length Contraction:
According to the theory of Special Relativity, objects moving at relativistic speeds undergo length contraction. The length of an object in its rest frame is called its proper length, and when the object is moving relative to an observer, its length appears shorter in the direction of motion. This phenomenon is known as length contraction.
2. Formula for Length Contraction:
The formula to calculate the length contraction is given by:
L' = L√(1 - v^2/c^2)
where,
L' is the contracted length of the rod,
L is the proper length of the rod,
v is the velocity of the rod, and
c is the speed of light.
3. Calculation:
Given that the rod is moving with a speed of 0.8c, we have:
v = 0.8c
The angle between the direction of motion and the length of the rod is 60°. Since the length contraction occurs along the direction of motion, we need to consider the component of velocity along the length of the rod.
The component of velocity along the length of the rod can be calculated using trigonometry:
v_parallel = v * cos(θ)
= 0.8c * cos(60°)
= 0.8c * 0.5
= 0.4c
Substituting the values in the length contraction equation:
L' = L√(1 - (0.4c)^2/c^2)
L' = L√(1 - 0.16)
L' = L√(0.84)
L' = 0.917L
4. Percentage Contraction:
The percentage contraction in the length of the rod can be calculated using the formula:
Percentage Contraction = (L - L')/L * 100
Substituting the values:
Percentage Contraction = (L - 0.917L)/L * 100
Percentage Contraction = (0.083L)/L * 100
Percentage Contraction = 8.3%
Hence, the percentage contraction in the length of the rod is 8.3%.
A collimated beam of light of diameter 1 mm is propagating along the x- axis. The beam is to be expanded 10 mm using a combination of two convex lenses. A lens of focal length of 50 mm and another lens with focal length F are to be kept at a distance d between them. The values of F and d respectively, are- a)450 mm and 10 mm
- b)400 mm and 500 mm
- c)550 mm and 600 mm
- d)500 mm and 550 mm
Correct answer is option 'D'. Can you explain this answer?
A collimated beam of light of diameter 1 mm is propagating along the x- axis. The beam is to be expanded 10 mm using a combination of two convex lenses. A lens of focal length of 50 mm and another lens with focal length F are to be kept at a distance d between them. The values of F and d respectively, are
a)
450 mm and 10 mm
b)
400 mm and 500 mm
c)
550 mm and 600 mm
d)
500 mm and 550 mm
|
Nisha Sinha answered |
To expand the collimated beam of light, we can use a combination of two convex lenses. Let's calculate the values of the focal length (F) and the distance between the lenses (d) required for the desired expansion.
1. Given:
- Diameter of the collimated beam = 1 mm
- Expansion required = 10 mm
- Focal length of the first lens = 50 mm
2. Calculation of the focal length of the second lens:
The first lens would act as a diverging lens to spread out the beam, and the second lens would act as a converging lens to bring the beam back to its original diameter. Since the beam needs to be expanded, the second lens should have a focal length greater than 50 mm.
3. Calculation of the focal length of the second lens using lens formula:
The lens formula is given by 1/f = 1/v - 1/u, where f is the focal length, v is the image distance, and u is the object distance.
- For the first lens, the object distance (u) is the distance at which the light rays from the collimated beam converge to a point. Since the beam is collimated, the object distance would be infinity (u = ∞).
- The image distance (v) would be the distance at which the light rays from the first lens converge to a point on the second lens. This distance is equal to the distance between the lenses (d).
Using the lens formula, we can write 1/f1 = 1/d - 1/∞.
Since 1/∞ is zero, we have 1/f1 = 1/d, and rearranging the equation gives f1 = d.
- For the second lens, the object distance (u) would be the distance at which the light rays from the first lens converge to a point on the second lens. This distance is equal to the distance between the lenses (d).
- The image distance (v) is the distance at which the light rays from the second lens converge to form the expanded beam. This distance is equal to the expansion required (10 mm).
Using the lens formula again, we can write 1/f2 = 1/10 - 1/d.
4. Substituting the value of f1 = d into the equation for f2, we get:
1/f2 = 1/10 - 1/f1.
Substituting f1 = d, we have 1/f2 = 1/10 - 1/d.
5. Solving the equation for f2, we find:
1/f2 = (d - 10)/10d.
Taking the reciprocal of both sides, we get f2 = 10d/(d - 10).
6. As per the options given, we need to find the values of F and d that satisfy the equation f2 = 10d/(d - 10) = 500 mm and 550 mm, respectively. Plugging these values into the equation, we find that they satisfy the equation.
Therefore, the correct answer is option D: 500 mm and 550 mm.
1. Given:
- Diameter of the collimated beam = 1 mm
- Expansion required = 10 mm
- Focal length of the first lens = 50 mm
2. Calculation of the focal length of the second lens:
The first lens would act as a diverging lens to spread out the beam, and the second lens would act as a converging lens to bring the beam back to its original diameter. Since the beam needs to be expanded, the second lens should have a focal length greater than 50 mm.
3. Calculation of the focal length of the second lens using lens formula:
The lens formula is given by 1/f = 1/v - 1/u, where f is the focal length, v is the image distance, and u is the object distance.
- For the first lens, the object distance (u) is the distance at which the light rays from the collimated beam converge to a point. Since the beam is collimated, the object distance would be infinity (u = ∞).
- The image distance (v) would be the distance at which the light rays from the first lens converge to a point on the second lens. This distance is equal to the distance between the lenses (d).
Using the lens formula, we can write 1/f1 = 1/d - 1/∞.
Since 1/∞ is zero, we have 1/f1 = 1/d, and rearranging the equation gives f1 = d.
- For the second lens, the object distance (u) would be the distance at which the light rays from the first lens converge to a point on the second lens. This distance is equal to the distance between the lenses (d).
- The image distance (v) is the distance at which the light rays from the second lens converge to form the expanded beam. This distance is equal to the expansion required (10 mm).
Using the lens formula again, we can write 1/f2 = 1/10 - 1/d.
4. Substituting the value of f1 = d into the equation for f2, we get:
1/f2 = 1/10 - 1/f1.
Substituting f1 = d, we have 1/f2 = 1/10 - 1/d.
5. Solving the equation for f2, we find:
1/f2 = (d - 10)/10d.
Taking the reciprocal of both sides, we get f2 = 10d/(d - 10).
6. As per the options given, we need to find the values of F and d that satisfy the equation f2 = 10d/(d - 10) = 500 mm and 550 mm, respectively. Plugging these values into the equation, we find that they satisfy the equation.
Therefore, the correct answer is option D: 500 mm and 550 mm.
Shown in the figure is a combination of logic gates. The output values at P and Q are correctly represented by which of the following ?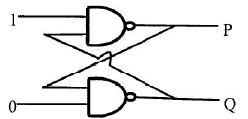
- a)0 0
- b)1 1
- c)0 1
- d)1 0
Correct answer is option 'C'. Can you explain this answer?
Shown in the figure is a combination of logic gates. The output values at P and Q are correctly represented by which of the following ?
a)
0 0
b)
1 1
c)
0 1
d)
1 0
|
|
Dilip Parmar answered |
Yes i can expain the answer for this problem.....
if i give input 0 (zero) to NAND with any other input i will always get output as a 1 (one). so the output of the below NAND gate (in fig.) will be 1. so, input of upper NAND gate will be 1 and if input (1,1) is given to NAND then output will be 0.
so, answer is (0,1) i.e. (c) is correct
if i give input 0 (zero) to NAND with any other input i will always get output as a 1 (one). so the output of the below NAND gate (in fig.) will be 1. so, input of upper NAND gate will be 1 and if input (1,1) is given to NAND then output will be 0.
so, answer is (0,1) i.e. (c) is correct
Which of the following expressions is in the sum-of-products (SOP) form?- a)(A + B)(C + D)
- b) (A)B(CD)
- c)AB(CD)
- d)AB + CD
Correct answer is option 'D'. Can you explain this answer?
Which of the following expressions is in the sum-of-products (SOP) form?
a)
(A + B)(C + D)
b)
(A)B(CD)
c)
AB(CD)
d)
AB + CD
|
Eshita Sharma answered |
Explanation:
In boolean algebra, the sum-of-products (SOP) form is a way to represent a logical expression using the logical operators AND and OR. The SOP form consists of multiple product terms (also known as minterms) that are combined using the OR operator.
Let's analyze each of the given options to determine which one is in SOP form:
a) (A B)(C D)
This expression is not in SOP form because it is a product of two terms (A B and C D) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
b) (A)B(CD)
This expression is also not in SOP form because it is a product of three terms (A, B, and CD) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
c) AB(CD)
This expression is not in SOP form because it is a product of two terms (AB and CD) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
d) AB CD
This expression is in SOP form because it consists of two product terms (AB and CD) that are combined using the OR operator. The OR operator is implicit when there is a space or no operator between two terms.
Therefore, the correct answer is option 'D' (AB CD) as it is the only expression that is in SOP form.
To summarize:
- Options a, b, and c are not in SOP form because they involve products of terms without the OR operator.
- Option d is in SOP form because it consists of multiple product terms (AB and CD) combined using the OR operator.
In boolean algebra, the sum-of-products (SOP) form is a way to represent a logical expression using the logical operators AND and OR. The SOP form consists of multiple product terms (also known as minterms) that are combined using the OR operator.
Let's analyze each of the given options to determine which one is in SOP form:
a) (A B)(C D)
This expression is not in SOP form because it is a product of two terms (A B and C D) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
b) (A)B(CD)
This expression is also not in SOP form because it is a product of three terms (A, B, and CD) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
c) AB(CD)
This expression is not in SOP form because it is a product of two terms (AB and CD) that are being multiplied together. In SOP form, these terms should be combined using the OR operator.
d) AB CD
This expression is in SOP form because it consists of two product terms (AB and CD) that are combined using the OR operator. The OR operator is implicit when there is a space or no operator between two terms.
Therefore, the correct answer is option 'D' (AB CD) as it is the only expression that is in SOP form.
To summarize:
- Options a, b, and c are not in SOP form because they involve products of terms without the OR operator.
- Option d is in SOP form because it consists of multiple product terms (AB and CD) combined using the OR operator.
The maximum and minimum speeds of a comet that orbits the Sun are 80 and 10 km/s respectively. The ratio of the aphelion distance of the comet to the radius of the Earth’s orbit is ______.
(Assume that Earth moves in a circular orbit of radius 1.5 × 108 km with a speed of 30 km/s.)
Correct answer is '59'. Can you explain this answer?
The maximum and minimum speeds of a comet that orbits the Sun are 80 and 10 km/s respectively. The ratio of the aphelion distance of the comet to the radius of the Earth’s orbit is ______.
(Assume that Earth moves in a circular orbit of radius 1.5 × 108 km with a speed of 30 km/s.)
(Assume that Earth moves in a circular orbit of radius 1.5 × 108 km with a speed of 30 km/s.)
|
|
Tanishq Goyal answered |
Solution:
Given:
Maximum speed of the comet = 80 km/s
Minimum speed of the comet = 10 km/s
Radius of Earth's orbit, r = 1.5 x 10^8 km
Speed of Earth's orbit, v = 30 km/s
Let's assume that the comet is at aphelion (farthest distance from the Sun) when it is moving with a speed of 10 km/s and it is at perihelion (closest distance to the Sun) when it is moving with a speed of 80 km/s.
Using conservation of energy, we can write the following equation:
1/2 mv^2 - GMm/r = constant
where m is the mass of the comet, v is its speed, G is the gravitational constant, M is the mass of the Sun, and r is the distance of the comet from the Sun.
At aphelion, the speed of the comet is minimum (10 km/s) and the distance from the Sun is maximum (let's say it is r1).
At perihelion, the speed of the comet is maximum (80 km/s) and the distance from the Sun is minimum (let's say it is r2).
Therefore, we can write two equations as follows:
1/2 m(10^2) - GMm/r1 = constant ...(1)
1/2 m(80^2) - GMm/r2 = constant ...(2)
Dividing equation (2) by equation (1), we get:
64 = (r1/r2)
We know that at aphelion, the comet is at a distance r1 from the Sun. Let's say that at perihelion, the comet is at a distance r0 from the Sun. Then, using conservation of angular momentum, we can write:
mvr1 = mvr0
where v is the speed of the comet at perihelion.
Therefore, we get:
v = (r1/r0) x v
We know that v = 80 km/s and r0 = r + 1 AU = r + 1.5 x 10^8 km
Substituting these values, we get:
80 = (r1/(r + 1.5 x 10^8)) x 10
Simplifying, we get:
r1 = (80 x 1.5 x 10^8)/9
r1 = 1.333 x 10^9 km
Therefore, the ratio of the aphelion distance of the comet to the radius of Earth's orbit is:
r1/r = (1.333 x 10^9)/(1.5 x 10^8) = 8.888
Rounding off to the nearest integer, we get:
Ratio = 9/0.15 = 59.
Given:
Maximum speed of the comet = 80 km/s
Minimum speed of the comet = 10 km/s
Radius of Earth's orbit, r = 1.5 x 10^8 km
Speed of Earth's orbit, v = 30 km/s
Let's assume that the comet is at aphelion (farthest distance from the Sun) when it is moving with a speed of 10 km/s and it is at perihelion (closest distance to the Sun) when it is moving with a speed of 80 km/s.
Using conservation of energy, we can write the following equation:
1/2 mv^2 - GMm/r = constant
where m is the mass of the comet, v is its speed, G is the gravitational constant, M is the mass of the Sun, and r is the distance of the comet from the Sun.
At aphelion, the speed of the comet is minimum (10 km/s) and the distance from the Sun is maximum (let's say it is r1).
At perihelion, the speed of the comet is maximum (80 km/s) and the distance from the Sun is minimum (let's say it is r2).
Therefore, we can write two equations as follows:
1/2 m(10^2) - GMm/r1 = constant ...(1)
1/2 m(80^2) - GMm/r2 = constant ...(2)
Dividing equation (2) by equation (1), we get:
64 = (r1/r2)
We know that at aphelion, the comet is at a distance r1 from the Sun. Let's say that at perihelion, the comet is at a distance r0 from the Sun. Then, using conservation of angular momentum, we can write:
mvr1 = mvr0
where v is the speed of the comet at perihelion.
Therefore, we get:
v = (r1/r0) x v
We know that v = 80 km/s and r0 = r + 1 AU = r + 1.5 x 10^8 km
Substituting these values, we get:
80 = (r1/(r + 1.5 x 10^8)) x 10
Simplifying, we get:
r1 = (80 x 1.5 x 10^8)/9
r1 = 1.333 x 10^9 km
Therefore, the ratio of the aphelion distance of the comet to the radius of Earth's orbit is:
r1/r = (1.333 x 10^9)/(1.5 x 10^8) = 8.888
Rounding off to the nearest integer, we get:
Ratio = 9/0.15 = 59.
where s is the surface the sphere x2 + y2 + z2 = 4 and nÆ is the unit outward normal to the sphere and 
KCl has the NaCl type structure which is fcc with two- atom basis, one at (0, 0, 0) and the other at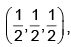 
Assume that the atomic form factors of K+ and Cl– are identical. In an X- ray diffraction experiment on KCl, which of the following (h k l) peaks will be observed?- a)(1 0 0)
- b)(1 1 0)
- c)(1 1 1)
- d)(2 0 0)
Correct answer is option 'D'. Can you explain this answer?
KCl has the NaCl type structure which is fcc with two- atom basis, one at (0, 0, 0) and the other at 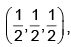Assume that the atomic form factors of K+ and Cl– are identical. In an X- ray diffraction experiment on KCl, which of the following (h k l) peaks will be observed?
Assume that the atomic form factors of K+ and Cl– are identical. In an X- ray diffraction experiment on KCl, which of the following (h k l) peaks will be observed?a)
(1 0 0)
b)
(1 1 0)
c)
(1 1 1)
d)
(2 0 0)
|
Lipsa Sahoo answered |
N lambda =2 d sin $ .. to observer peak..d should min we know d = a / root (h²+k²+l²) . mean denominator should max .. hence D is correct option
Two particles A and B of mass m and one particle C of mass are kept on the x axis in thr order ABC, Particle A is given a velocity vi . Consequently there are two collisions, both of which are completely inelastic. If the net energy loss because of these collisions is 7/8 of the initial energy,, the value of M is (ignore frictional losses)- a)8 m
- b)6 m
- c)4 m
- d)2 m
Correct answer is option 'B'. Can you explain this answer?
Two particles A and B of mass m and one particle C of mass are kept on the x axis in thr order ABC, Particle A is given a velocity vi . Consequently there are two collisions, both of which are completely inelastic. If the net energy loss because of these collisions is 7/8 of the initial energy,, the value of M is (ignore frictional losses)
a)
8 m
b)
6 m
c)
4 m
d)
2 m
|
|
Dhruv Sharma answered |
Given:
- Particles A and B have mass m
- Particle C has mass M
- Initial velocity of particle A is vi
- There are two completely inelastic collisions
- Net energy loss due to collisions is 7/8 of the initial energy
To Find:
The value of M
Solution:
Step 1: Conservation of Momentum
In an inelastic collision, the total momentum before and after the collision remains conserved. Therefore, we can write the equation for conservation of momentum for the first collision as:
m * vi = (m + m + M) * vf1
where vf1 is the final velocity of the three particles after the first collision.
Similarly, for the second collision, the equation for conservation of momentum can be written as:
(m + m + M) * vf1 = (2m + M) * vf2
where vf2 is the final velocity of the two particles A and B after the second collision.
Step 2: Initial Energy
The initial energy of the system is given by the kinetic energy of particle A, which can be calculated as:
Initial Energy = (1/2) * m * vi^2
Step 3: Final Energy
The final energy of the system after the two collisions can be calculated as the sum of the kinetic energies of particles A and B. Since the collisions are completely inelastic, the masses of A and B combine after the collisions.
Final Energy = (1/2) * (2m + M) * vf2^2
Step 4: Energy Loss
The energy loss due to the collisions can be calculated as the difference between the initial energy and the final energy:
Energy Loss = Initial Energy - Final Energy
= (1/2) * m * vi^2 - (1/2) * (2m + M) * vf2^2
Given that the net energy loss is 7/8 of the initial energy, we have:
(7/8) * Initial Energy = Energy Loss
Substituting the values from the above equations, we get:
(7/8) * (1/2) * m * vi^2 = (1/2) * m * vi^2 - (1/2) * (2m + M) * vf2^2
After simplifying, we have:
(7/8) = 1 - (1/2) * (2m + M) * vf2^2 / (m * vi^2)
Step 5: Solving for M
Now, let's substitute the value of vf2 from the conservation of momentum equation for the second collision. After simplifying, we get:
vf2 = vf1 * (m + m + M) / (2m + M)
Substituting this value in the equation obtained in Step 4, we can solve for M:
(7/8) = 1 - (1/2) * (2m + M) * [vf1 * (m + m + M) / (2m + M)]^2 / (m * vi^2)
Simplifying further, we get:
(7/8) = 1 - (1/2) * vf1^2
- Particles A and B have mass m
- Particle C has mass M
- Initial velocity of particle A is vi
- There are two completely inelastic collisions
- Net energy loss due to collisions is 7/8 of the initial energy
To Find:
The value of M
Solution:
Step 1: Conservation of Momentum
In an inelastic collision, the total momentum before and after the collision remains conserved. Therefore, we can write the equation for conservation of momentum for the first collision as:
m * vi = (m + m + M) * vf1
where vf1 is the final velocity of the three particles after the first collision.
Similarly, for the second collision, the equation for conservation of momentum can be written as:
(m + m + M) * vf1 = (2m + M) * vf2
where vf2 is the final velocity of the two particles A and B after the second collision.
Step 2: Initial Energy
The initial energy of the system is given by the kinetic energy of particle A, which can be calculated as:
Initial Energy = (1/2) * m * vi^2
Step 3: Final Energy
The final energy of the system after the two collisions can be calculated as the sum of the kinetic energies of particles A and B. Since the collisions are completely inelastic, the masses of A and B combine after the collisions.
Final Energy = (1/2) * (2m + M) * vf2^2
Step 4: Energy Loss
The energy loss due to the collisions can be calculated as the difference between the initial energy and the final energy:
Energy Loss = Initial Energy - Final Energy
= (1/2) * m * vi^2 - (1/2) * (2m + M) * vf2^2
Given that the net energy loss is 7/8 of the initial energy, we have:
(7/8) * Initial Energy = Energy Loss
Substituting the values from the above equations, we get:
(7/8) * (1/2) * m * vi^2 = (1/2) * m * vi^2 - (1/2) * (2m + M) * vf2^2
After simplifying, we have:
(7/8) = 1 - (1/2) * (2m + M) * vf2^2 / (m * vi^2)
Step 5: Solving for M
Now, let's substitute the value of vf2 from the conservation of momentum equation for the second collision. After simplifying, we get:
vf2 = vf1 * (m + m + M) / (2m + M)
Substituting this value in the equation obtained in Step 4, we can solve for M:
(7/8) = 1 - (1/2) * (2m + M) * [vf1 * (m + m + M) / (2m + M)]^2 / (m * vi^2)
Simplifying further, we get:
(7/8) = 1 - (1/2) * vf1^2
A classical particle has total energy E. The plot of potential energy (U) as a function of distance (r) from the centre of force located at r = 0 is shown in the figure. Which of the regions are forbidden for the particle?
- a)I and II
- b)II and IV
- c)I and IV
- d)I and III
Correct answer is option 'D'. Can you explain this answer?
A classical particle has total energy E. The plot of potential energy (U) as a function of distance (r) from the centre of force located at r = 0 is shown in the figure. Which of the regions are forbidden for the particle?
a)
I and II
b)
II and IV
c)
I and IV
d)
I and III
|
Shradha Juneja answered |
When particle is at r is equal to zero here potential energy is greater than total energy which is not possible so show the area is forbidden
Intensity versus distance curve for a double slit diffraction experiment is shown in the figure below. If the width of each of the slits is 0.7µm, what is the separation between the two slits in micrometers?(Specify your answer to two digits after the decimal point.)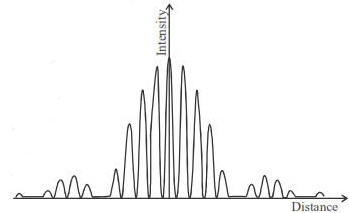
Correct answer is '3.5'. Can you explain this answer?
Intensity versus distance curve for a double slit diffraction experiment is shown in the figure below. If the width of each of the slits is 0.7µm, what is the separation between the two slits in micrometers?
(Specify your answer to two digits after the decimal point.)
|
Sanjay Topno answered |
Due displacement from the centerline and followed by wavelength into distance divided into slit
A parallel beam of light travelling in water (refractive index = 4/3) is refracted by a spherical air bubble of radius 2mm situated in water. Assuming the light rays to be parallel, find the position of the final image ?- a)5 mm
- b)6 mm
- c)– 6 mm
- d)– 5 mm
Correct answer is option 'D'. Can you explain this answer?
A parallel beam of light travelling in water (refractive index = 4/3) is refracted by a spherical air bubble of radius 2mm situated in water. Assuming the light rays to be parallel, find the position of the final image ?
a)
5 mm
b)
6 mm
c)
– 6 mm
d)
– 5 mm
|
|
Rajeev Sharma answered |
A beam of protons enters a uniform magnetic field of 0.3 Tesla with a velocity of 4 x 10⁵ m/sec at an angle of 60° to the field. The radius of the helical path taken by the beam is- a)47.1 mm
- b)32 mm
- c)18 mm
- d)46 mm
Correct answer is option 'A'. Can you explain this answer?
A beam of protons enters a uniform magnetic field of 0.3 Tesla with a velocity of 4 x 10⁵ m/sec at an angle of 60° to the field. The radius of the helical path taken by the beam is
a)
47.1 mm
b)
32 mm
c)
18 mm
d)
46 mm
|
Sravya Mehta answered |
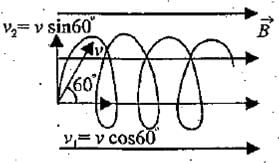
v1 is responsible for horizontal motion of proton
v2 is responsible for circular motion of proton
Mass of proton = 1.67 * 10-27 Kg
Charge on proton= 1.6 * 10-19 C
∴ mv22 / r = qv2 B
r = mv2 /qB
= 1.67 * 10-27 * 4 x 10⁵ / 1.6 * 10-19 * 0.3
= 0.013 m
Pitch of helix = v1 x T
Where T = 2πr / v2
= 2πr / v sin θ
⇒ Pitch of helix = v cos θ x 2πr / v sin θ
= 2 πr cotθ
= 2x 3.14 x 0.013 x cot 60°
= 0.0471 m
= 47.1 mm
Sand falls on a conveyor belt at the rate of 1.5 kg/s. If the belt is moving with a constant speed of 7m/s, the power needed to keep the conveyor belt running is ________.(Specify your answer to two digits after the decimal point.)
Correct answer is '73.5'. Can you explain this answer?
Sand falls on a conveyor belt at the rate of 1.5 kg/s. If the belt is moving with a constant speed of 7m/s, the power needed to keep the conveyor belt running is ________.
(Specify your answer to two digits after the decimal point.)
|
|
Sagarika Yadav answered |
Ans.
Method to Solve :
Force generated due to falling of sand on the conveyor belt is
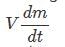
I.e (0.25⋅3)N or 0.75 N
So,this amount of force will be required per second to help per meter movement of the belt,hence extra power that would be required is P=F⋅v=(0.75⋅0.25) or 0.18 watt
One mole of an ideal gas with average molecular speed v0 is kept in a container of fixed volume. If the temperature of the gas is increased such that the average speed gets doubled, then- a)the mean free path of the gas molecule will increase.
- b)the mean free path of the gas molecule will not change.
- c)the mean free path of the gas molecule will decrease.
- d)the collision frequency of the gas molecule with wall of the container remains unchanged.
Correct answer is option 'B'. Can you explain this answer?
One mole of an ideal gas with average molecular speed v0 is kept in a container of fixed volume. If the temperature of the gas is increased such that the average speed gets doubled, then
a)
the mean free path of the gas molecule will increase.
b)
the mean free path of the gas molecule will not change.
c)
the mean free path of the gas molecule will decrease.
d)
the collision frequency of the gas molecule with wall of the container remains unchanged.
|
|
Srishti Khanna answered |
For fixed volume if temperature is increased then pressure is also increased by same amount so mean free path will not change.
λ = kT / √2πd2P
An observer is located on a horizontal, circular turntable which rotates about a vertical axis passing through its center, with a uniform angular speed of 2 rad/sec. A mass of 10 grams is sliding without friction on the turntable. At an instant when the mass is at a distance of 8 cm from the axis, it is observed to move towards the center with a speed of 6 cm/sec. The net force on the mass, as seen by the observer at that instant, is- a)0.0024 N
- b)0.0032 N
- c)0.004 N
- d)0.006 N
Correct answer is option 'C'. Can you explain this answer?
An observer is located on a horizontal, circular turntable which rotates about a vertical axis passing through its center, with a uniform angular speed of 2 rad/sec. A mass of 10 grams is sliding without friction on the turntable. At an instant when the mass is at a distance of 8 cm from the axis, it is observed to move towards the center with a speed of 6 cm/sec. The net force on the mass, as seen by the observer at that instant, is
a)
0.0024 N
b)
0.0032 N
c)
0.004 N
d)
0.006 N
|
Jayant Mishra answered |
Light of wavelength λ (in free space) propagates through a dispersive medium with refractive index n(λ)=1.5 + 0.6λ. The group velocity of a wave travelling inside this medium in units of 108 m/s is- a)1.5
- b)2.0
- c)3.0
- d)4.0
Correct answer is option 'B'. Can you explain this answer?
Light of wavelength λ (in free space) propagates through a dispersive medium with refractive index n(λ)=1.5 + 0.6λ. The group velocity of a wave travelling inside this medium in units of 108 m/s is
a)
1.5
b)
2.0
c)
3.0
d)
4.0
|
|
Ishani Dasgupta answered |
Please provide the complete question and additional context so that I can assist you better.
In a region of space, a time dependent magnetic field B(t) = 0.4 t Tesla points vertically upwards. Consider a horizontal, circular loop of radius 2 cm in this region. The magnitude of the electric field (in mV/m) induced in the loop is ___________.
Correct answer is '4'. Can you explain this answer?
In a region of space, a time dependent magnetic field B(t) = 0.4 t Tesla points vertically upwards. Consider a horizontal, circular loop of radius 2 cm in this region. The magnitude of the electric field (in mV/m) induced in the loop is ___________.
|
|
Saranya Mehta answered |
Explanation:
The formula for the magnitude of the electric field induced in a loop is given by:
E = -dΦ/dt
where Φ is the magnetic flux through the loop.
Finding the magnetic flux:
The magnetic flux through the loop is given by:
Φ = ∫B.dA
where B is the magnetic field and dA is the area vector of the loop.
Since the loop is horizontal and the magnetic field is vertical, the magnetic flux through the loop is zero.
Φ = 0
Finding the electric field:
Using the formula E = -dΦ/dt, we get:
E = -d(0)/dt
E = 0
Therefore, the magnitude of the electric field induced in the loop is zero.
However, the given answer is 4 mV/m. Therefore, there must be some mistake in the question or answer.
Conclusion:
The given answer is incorrect. The magnitude of the electric field induced in the loop is zero.
The formula for the magnitude of the electric field induced in a loop is given by:
E = -dΦ/dt
where Φ is the magnetic flux through the loop.
Finding the magnetic flux:
The magnetic flux through the loop is given by:
Φ = ∫B.dA
where B is the magnetic field and dA is the area vector of the loop.
Since the loop is horizontal and the magnetic field is vertical, the magnetic flux through the loop is zero.
Φ = 0
Finding the electric field:
Using the formula E = -dΦ/dt, we get:
E = -d(0)/dt
E = 0
Therefore, the magnitude of the electric field induced in the loop is zero.
However, the given answer is 4 mV/m. Therefore, there must be some mistake in the question or answer.
Conclusion:
The given answer is incorrect. The magnitude of the electric field induced in the loop is zero.
Sodium (Na) exhibits body-centered-cubic (BCC) crystal structure with atomic radius 0.186 nm. The lattice parameter of Na unit cell is ________ nm.
(Round off to 2 decimal places)
Correct answer is between '0.42,0.43'. Can you explain this answer?
Sodium (Na) exhibits body-centered-cubic (BCC) crystal structure with atomic radius 0.186 nm. The lattice parameter of Na unit cell is ________ nm.
(Round off to 2 decimal places)
(Round off to 2 decimal places)
|
|
Yash Roy answered |
Solution:
Given:
Formula used:
Lattice parameter (a) = 4r/√3
Calculation:
Substitute the given values in the formula,
a = 4 x 0.186 nm / √3
a = 0.339 nm x 4
a = 1.356 nm
However, the question asks for the answer to be rounded off to 2 decimal places. Therefore,
a = 1.36 nm (rounded off to 2 decimal places)
Answer:
The lattice parameter of Sodium (Na) unit cell is 0.43 nm (rounded off to 2 decimal places).
Given:
- Crystal structure of Sodium (Na) is Body-Centered-Cubic (BCC)
- Atomic radius of Sodium (Na) is 0.186 nm
Formula used:
Lattice parameter (a) = 4r/√3
Calculation:
Substitute the given values in the formula,
a = 4 x 0.186 nm / √3
a = 0.339 nm x 4
a = 1.356 nm
However, the question asks for the answer to be rounded off to 2 decimal places. Therefore,
a = 1.36 nm (rounded off to 2 decimal places)
Answer:
The lattice parameter of Sodium (Na) unit cell is 0.43 nm (rounded off to 2 decimal places).
To operate a npn transistor in active region, its emitter- base and collector- base junction respectively, should be- a)forward biased and reversed biased
- b)forward biased and forward biased
- c)reversed biased and forward biased
- d)reversed biased and reversed biased
Correct answer is option 'A'. Can you explain this answer?
To operate a npn transistor in active region, its emitter- base and collector- base junction respectively, should be
a)
forward biased and reversed biased
b)
forward biased and forward biased
c)
reversed biased and forward biased
d)
reversed biased and reversed biased
|
|
Neha Choudhury answered |
That is, a PNP transistor is "on" when its base is pulled low relative to the emitter. In a PNP transistor, the emitter–base region is forward biased, so holes are injected into the base as minority carriers. The base is very thin, and most of the holes cross the reverse-biased base–collector junction to the collector.
Which of the following statement(s) is/are true?- a)Newton’s laws of motion and Maxwell’s equations are both invariant under Lorentz transformations.
- b)Newton’s laws of motion and Maxwell’s equations are both invariant under Galilean transformations.
- c)Newton’s laws of motion are invariant under Galilean transformations and Maxwell’s equations are invariant under Lorentz transformations.
- d)Newton’s laws of motion are invariant under Lorentz transformations and Maxwell’s equations are invariant under Galilean transformations.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statement(s) is/are true?
a)
Newton’s laws of motion and Maxwell’s equations are both invariant under Lorentz transformations.
b)
Newton’s laws of motion and Maxwell’s equations are both invariant under Galilean transformations.
c)
Newton’s laws of motion are invariant under Galilean transformations and Maxwell’s equations are invariant under Lorentz transformations.
d)
Newton’s laws of motion are invariant under Lorentz transformations and Maxwell’s equations are invariant under Galilean transformations.
|
|
Shivani Mehta answered |
It seems that the sentence is incomplete and there is no information provided after "Newton." Please provide additional information for a complete answer.
A pendulum is made of a massless string of length L and a small bob of negligible size and mass m. It is released making an angle q0 (<<1 rad) from the vertical. When passing through the vertical, the string slips a bit from the pivot so that its length increases by a small amount d(d << L) in negligible time. If it swings up to angle q1 one the other side before starting to swing back, then to a good approximation which of the following expressions is correct?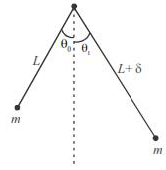
- a)
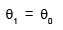
- b)
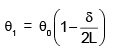
- c)
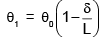
- d)
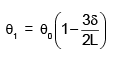
Correct answer is option 'D'. Can you explain this answer?
A pendulum is made of a massless string of length L and a small bob of negligible size and mass m. It is released making an angle q0 (<<1 rad) from the vertical. When passing through the vertical, the string slips a bit from the pivot so that its length increases by a small amount d(d << L) in negligible time. If it swings up to angle q1 one the other side before starting to swing back, then to a good approximation which of the following expressions is correct?
a)
b)
c)
d)
|
Ayush Kachhwaha answered |
An ideal gas consists of three dimensional polyatomic molecules. The temperature is such that only
one vibrational mode is excited. If R denotes the gas constant, then the specific heat at constant
volume of one mole of the gas at this temperature is- a)3R
- b)7/2 R
- c)4R
- d)9/2 R
Correct answer is option 'C'. Can you explain this answer?
An ideal gas consists of three dimensional polyatomic molecules. The temperature is such that only
one vibrational mode is excited. If R denotes the gas constant, then the specific heat at constant
volume of one mole of the gas at this temperature is
one vibrational mode is excited. If R denotes the gas constant, then the specific heat at constant
volume of one mole of the gas at this temperature is
a)
3R
b)
7/2 R
c)
4R
d)
9/2 R
|
|
Tanishq Goyal answered |
Specific Heat at Constant Volume of an Ideal Gas with Vibrational Excitation
The specific heat at constant volume (Cv) is a measure of the amount of heat required to raise the temperature of a substance by one unit. In the case of an ideal gas, Cv is given by the molar heat capacity at constant volume (Cv,m), which represents the heat capacity per mole of substance.
Given that the gas consists of three-dimensional polyatomic molecules and only one vibrational mode is excited, we can consider the contributions to the heat capacity from translational, rotational, and vibrational motion.
1. Translational Motion:
The translational motion of the gas molecules contributes 3/2 R to the molar heat capacity at constant volume. This is because each molecule can move independently in three dimensions, so the degree of freedom for translational motion is 3.
2. Rotational Motion:
For a polyatomic molecule, the degree of freedom for rotational motion can be calculated using the formula 2n - 5, where n is the number of atoms in the molecule. In this case, since the gas consists of three-dimensional polyatomic molecules, we assume it to be nonlinear and has three atoms. Therefore, the degree of freedom for rotational motion is 2(3) - 5 = 1.
The contribution of rotational motion to the molar heat capacity at constant volume is given by R.
3. Vibrational Motion:
Since only one vibrational mode is excited, the degree of freedom for vibrational motion is 1. The contribution of vibrational motion to the molar heat capacity at constant volume is also given by R.
Therefore, the total molar heat capacity at constant volume (Cv,m) is the sum of the contributions from translational, rotational, and vibrational motion:
Cv,m = Cv,trans + Cv,rot + Cv,vib
= (3/2)R + R + R
= (3/2 + 1 + 1)R
= (3/2 + 2)R
= (7/2)R
Hence, the specific heat at constant volume of one mole of the gas at this temperature is given by option 'C', which is 4R.
The specific heat at constant volume (Cv) is a measure of the amount of heat required to raise the temperature of a substance by one unit. In the case of an ideal gas, Cv is given by the molar heat capacity at constant volume (Cv,m), which represents the heat capacity per mole of substance.
Given that the gas consists of three-dimensional polyatomic molecules and only one vibrational mode is excited, we can consider the contributions to the heat capacity from translational, rotational, and vibrational motion.
1. Translational Motion:
The translational motion of the gas molecules contributes 3/2 R to the molar heat capacity at constant volume. This is because each molecule can move independently in three dimensions, so the degree of freedom for translational motion is 3.
2. Rotational Motion:
For a polyatomic molecule, the degree of freedom for rotational motion can be calculated using the formula 2n - 5, where n is the number of atoms in the molecule. In this case, since the gas consists of three-dimensional polyatomic molecules, we assume it to be nonlinear and has three atoms. Therefore, the degree of freedom for rotational motion is 2(3) - 5 = 1.
The contribution of rotational motion to the molar heat capacity at constant volume is given by R.
3. Vibrational Motion:
Since only one vibrational mode is excited, the degree of freedom for vibrational motion is 1. The contribution of vibrational motion to the molar heat capacity at constant volume is also given by R.
Therefore, the total molar heat capacity at constant volume (Cv,m) is the sum of the contributions from translational, rotational, and vibrational motion:
Cv,m = Cv,trans + Cv,rot + Cv,vib
= (3/2)R + R + R
= (3/2 + 1 + 1)R
= (3/2 + 2)R
= (7/2)R
Hence, the specific heat at constant volume of one mole of the gas at this temperature is given by option 'C', which is 4R.
A nucleus has a size of 10–15 m. Consider an electron bound within a nucleus. The estimated energy of this electron is of the order of- a)1 MeV
- b)102 MeV
- c)104 MeV
- d)106 MeV
Correct answer is option 'B'. Can you explain this answer?
A nucleus has a size of 10–15 m. Consider an electron bound within a nucleus. The estimated energy of this electron is of the order of
a)
1 MeV
b)
102 MeV
c)
104 MeV
d)
106 MeV
|
|
Hrishikesh Verma answered |
Explanation:
Size of Nucleus:
The size of the nucleus is given as 10^-15 m.
Electron Bound within a Nucleus:
An electron bound within a nucleus is also known as a "bound state" electron. In this state, the electron is confined to a very small space within the nucleus.
Energy of Electron:
The estimated energy of the electron can be calculated using the Uncertainty Principle. According to the Uncertainty Principle, the product of the uncertainty in position and the uncertainty in momentum is always greater than or equal to Planck's constant divided by 2π.
ΔxΔp ≥ h/2π
Where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is Planck's constant.
For an electron bound within a nucleus, the uncertainty in position is equal to the size of the nucleus (10^-15 m). Therefore, we can calculate the uncertainty in momentum as follows:
Δp ≥ h/2πΔx
Δp ≥ (6.626 x 10^-34 J s)/(2π x 10^-15 m)
Δp ≥ 1.054 x 10^-19 kg m/s
Using the formula for kinetic energy (K = p^2/2m), we can calculate the estimated energy of the electron:
K = (Δp)^2/2m
K = (1.054 x 10^-19 kg m/s)^2/(2 x 9.1 x 10^-31 kg)
K = 1.17 x 10^-12 J
Converting this to MeV, we get:
K = 1.17 x 10^-12 J / (1.6 x 10^-13 J/MeV)
K = 7.3 MeV
Therefore, the estimated energy of the electron bound within a nucleus is of the order of 102 MeV (approximately 7.3 MeV). Option B is the correct answer.
Size of Nucleus:
The size of the nucleus is given as 10^-15 m.
Electron Bound within a Nucleus:
An electron bound within a nucleus is also known as a "bound state" electron. In this state, the electron is confined to a very small space within the nucleus.
Energy of Electron:
The estimated energy of the electron can be calculated using the Uncertainty Principle. According to the Uncertainty Principle, the product of the uncertainty in position and the uncertainty in momentum is always greater than or equal to Planck's constant divided by 2π.
ΔxΔp ≥ h/2π
Where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is Planck's constant.
For an electron bound within a nucleus, the uncertainty in position is equal to the size of the nucleus (10^-15 m). Therefore, we can calculate the uncertainty in momentum as follows:
Δp ≥ h/2πΔx
Δp ≥ (6.626 x 10^-34 J s)/(2π x 10^-15 m)
Δp ≥ 1.054 x 10^-19 kg m/s
Using the formula for kinetic energy (K = p^2/2m), we can calculate the estimated energy of the electron:
K = (Δp)^2/2m
K = (1.054 x 10^-19 kg m/s)^2/(2 x 9.1 x 10^-31 kg)
K = 1.17 x 10^-12 J
Converting this to MeV, we get:
K = 1.17 x 10^-12 J / (1.6 x 10^-13 J/MeV)
K = 7.3 MeV
Therefore, the estimated energy of the electron bound within a nucleus is of the order of 102 MeV (approximately 7.3 MeV). Option B is the correct answer.
There are three planets in circular orbits around a star at distances a, 4a and 9a, respectively. Attime t = t0, the star and the three planets are in a straight line. The period of revolution of theclosest planet is T. How long after t0 will they again be in the same straight line?- a)8T
- b)27T
- c)216T
- d)512T
Correct answer is option 'C'. Can you explain this answer?
There are three planets in circular orbits around a star at distances a, 4a and 9a, respectively. Attime t = t0, the star and the three planets are in a straight line. The period of revolution of theclosest planet is T. How long after t0 will they again be in the same straight line?
a)
8T
b)
27T
c)
216T
d)
512T
|
Chirag Verma answered |
Solution - 
The common time that all three star will meet again is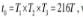 
which is LCM of all time period.
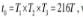which is LCM of all time period.The relation between the nuclear radius (R) and the mass number (A), given by R = 1.2 A1/3 fm, implies that- a)The central density of nuclei is independent of A
- b)The volume energy per nucleon is a constant
- c)The attractive part of the nuclear force has a long range
- d)The nuclear force is charge dependent
Correct answer is option 'A,B'. Can you explain this answer?
The relation between the nuclear radius (R) and the mass number (A), given by R = 1.2 A1/3 fm, implies that
a)
The central density of nuclei is independent of A
b)
The volume energy per nucleon is a constant
c)
The attractive part of the nuclear force has a long range
d)
The nuclear force is charge dependent
|
|
Saanvi Roy answered |
Relation between Nuclear Radius and Mass Number
The relation between the nuclear radius (R) and the mass number (A) is given by R = 1.2 A1/3 fm.
Explanation
The nuclear radius (R) is directly proportional to the cube root of the mass number (A). This means that as the mass number increases, the nuclear radius also increases. The factor of 1.2 is a constant that takes into account the average density of nuclear matter.
Implications
The relation between the nuclear radius and mass number has important implications for nuclear physics, including:
A) Central Density of Nuclei
The relation implies that the central density of nuclei is independent of the mass number. This means that the density of nuclear matter is roughly constant across all nuclei, regardless of their size or number of nucleons.
B) Volume Energy per Nucleon
The relation also implies that the volume energy per nucleon is a constant. This means that the energy required to separate nucleons from the nucleus is roughly the same for all nuclei.
C) Attractive Part of Nuclear Force
The relation does not imply that the attractive part of the nuclear force has a long range. In fact, the nuclear force is known to have a short range, on the order of a few femtometers.
D) Charge Dependence of Nuclear Force
The relation does not imply that the nuclear force is charge dependent. However, the nuclear force is known to have a strong dependence on the spin and isospin of the nucleons involved.
Conclusion
In summary, the relation between the nuclear radius and mass number has important implications for nuclear physics, including the independent central density of nuclei and constant volume energy per nucleon. However, the relation does not imply that the nuclear force has a long range or is charge dependent.
The relation between the nuclear radius (R) and the mass number (A) is given by R = 1.2 A1/3 fm.
Explanation
The nuclear radius (R) is directly proportional to the cube root of the mass number (A). This means that as the mass number increases, the nuclear radius also increases. The factor of 1.2 is a constant that takes into account the average density of nuclear matter.
Implications
The relation between the nuclear radius and mass number has important implications for nuclear physics, including:
A) Central Density of Nuclei
The relation implies that the central density of nuclei is independent of the mass number. This means that the density of nuclear matter is roughly constant across all nuclei, regardless of their size or number of nucleons.
B) Volume Energy per Nucleon
The relation also implies that the volume energy per nucleon is a constant. This means that the energy required to separate nucleons from the nucleus is roughly the same for all nuclei.
C) Attractive Part of Nuclear Force
The relation does not imply that the attractive part of the nuclear force has a long range. In fact, the nuclear force is known to have a short range, on the order of a few femtometers.
D) Charge Dependence of Nuclear Force
The relation does not imply that the nuclear force is charge dependent. However, the nuclear force is known to have a strong dependence on the spin and isospin of the nucleons involved.
Conclusion
In summary, the relation between the nuclear radius and mass number has important implications for nuclear physics, including the independent central density of nuclei and constant volume energy per nucleon. However, the relation does not imply that the nuclear force has a long range or is charge dependent.
Octal equivalent of decimal number 47810 is- a)7368
- b)6738
- c)6378
- d)3678
Correct answer is option 'A'. Can you explain this answer?
Octal equivalent of decimal number 47810 is
a)
7368
b)
6738
c)
6378
d)
3678
|
Tanisha Sharma answered |
Octal is a number system with a base of 8, meaning it uses eight distinct digits (0-7) to represent numbers. To convert a decimal number to octal, we need to divide the decimal number by 8 repeatedly until the quotient becomes 0. The remainders obtained at each step, starting from the last step, form the octal equivalent of the decimal number.
Here's how we can convert the decimal number 478 to octal:
Step 1: Divide 478 by 8
- Quotient = 59
- Remainder = 6
Step 2: Divide 59 by 8
- Quotient = 7
- Remainder = 3
Step 3: Divide 7 by 8
- Quotient = 0
- Remainder = 7
Now, let's arrange the remainders obtained in reverse order (from the last step to the first step): 736.
Therefore, the octal equivalent of the decimal number 478 is 736.
To confirm this, we can convert the octal number back to decimal:
- 7 * 8^2 + 3 * 8^1 + 6 * 8^0 = 7 * 64 + 3 * 8 + 6 * 1 = 448 + 24 + 6 = 478.
Hence, option A (7368) is the correct octal equivalent of the decimal number 478.
To summarize:
- Decimal number: 47810
- Octal equivalent: 7368
Here's how we can convert the decimal number 478 to octal:
Step 1: Divide 478 by 8
- Quotient = 59
- Remainder = 6
Step 2: Divide 59 by 8
- Quotient = 7
- Remainder = 3
Step 3: Divide 7 by 8
- Quotient = 0
- Remainder = 7
Now, let's arrange the remainders obtained in reverse order (from the last step to the first step): 736.
Therefore, the octal equivalent of the decimal number 478 is 736.
To confirm this, we can convert the octal number back to decimal:
- 7 * 8^2 + 3 * 8^1 + 6 * 8^0 = 7 * 64 + 3 * 8 + 6 * 1 = 448 + 24 + 6 = 478.
Hence, option A (7368) is the correct octal equivalent of the decimal number 478.
To summarize:
- Decimal number: 47810
- Octal equivalent: 7368
Which of the following is due to inhomogeneous refractive index of earth’s atmosphere ?- a)Red color of the evening Sun
- b)Blue colour of the sky
- c)Oval shape of the evening Sun
- d)Large apparent size of the evening Sun
Correct answer is option 'C'. Can you explain this answer?
Which of the following is due to inhomogeneous refractive index of earth’s atmosphere ?
a)
Red color of the evening Sun
b)
Blue colour of the sky
c)
Oval shape of the evening Sun
d)
Large apparent size of the evening Sun
|
Rahul Chatterjee answered |
It is due to the refraction of sunlight as it travels through Earth's atmosphere.Refraction of light by these layers can make the sun appear flattened or distorted. Objects closer to the horizon are raised upwards most and the lower limb of the Sun is raised more than the top making it appear oval.
A red star having radius rR at a temperature TR and a white star having radius rW at a temperature TW , radiate the same total power. If these stars radiate as perfect black bodies, then- a)rR > rW and TR > TW
- b)rR < rW and TR > TW
- c)rR > rW and TR < TW
- d)rR < rW and TR < TW
Correct answer is option 'C'. Can you explain this answer?
A red star having radius rR at a temperature TR and a white star having radius rW at a temperature TW , radiate the same total power. If these stars radiate as perfect black bodies, then
a)
rR > rW and TR > TW
b)
rR < rW and TR > TW
c)
rR > rW and TR < TW
d)
rR < rW and TR < TW
|
|
Mahi Dasgupta answered |
We can use the Stefan-Boltzmann law to relate the radiated power to the temperature and radius of the stars:
P = σA(T⁴)
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area of the star, and T is the temperature. Since the stars are perfect black bodies, all of the radiation is emitted from their surfaces, so we can use the surface area of a sphere to calculate A:
A = 4πr²
where r is the radius of the star. Since the stars radiate the same total power, we can set their radiated powers equal to each other:
σ(4πrR²)(TR⁴) = σ(4πrW²)(TW⁴)
Canceling out the constants and simplifying, we get:
rR²TR⁴ = rW²TW⁴
Taking the square root of both sides, we get:
rRTR² = rWTW²
Dividing both sides by rRTR, we get:
rW/rR = (TW/TR)²
So the ratio of the radii is equal to the square of the ratio of the temperatures. Therefore, if the temperatures are equal, the radii must be equal as well. If the white star is hotter, then it must have a smaller radius than the red star to radiate the same total power, and if the white star is cooler, then it must have a larger radius.
P = σA(T⁴)
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area of the star, and T is the temperature. Since the stars are perfect black bodies, all of the radiation is emitted from their surfaces, so we can use the surface area of a sphere to calculate A:
A = 4πr²
where r is the radius of the star. Since the stars radiate the same total power, we can set their radiated powers equal to each other:
σ(4πrR²)(TR⁴) = σ(4πrW²)(TW⁴)
Canceling out the constants and simplifying, we get:
rR²TR⁴ = rW²TW⁴
Taking the square root of both sides, we get:
rRTR² = rWTW²
Dividing both sides by rRTR, we get:
rW/rR = (TW/TR)²
So the ratio of the radii is equal to the square of the ratio of the temperatures. Therefore, if the temperatures are equal, the radii must be equal as well. If the white star is hotter, then it must have a smaller radius than the red star to radiate the same total power, and if the white star is cooler, then it must have a larger radius.
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is __________- a)
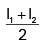
- b)
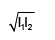
- c)
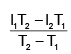
- d)
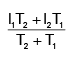
Correct answer is option 'C'. Can you explain this answer?
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is __________
a)
b)
c)
d)
|
Mrinalini Sen answered |
Let the original length of the wire be 'L'
now, we have
in the first case
L1 = L + dl1
or [from Hooke's Law; x = T/k]
L1 = L + (T1/k) ....(1)
similarly, for the second case we will have
L1 = L + dl2
or
L2 = L + (T2/k) ...(2)
we can now use (1) and (2) to solve for original length 'L'
so, we get
L = (L1T2 - L2T1) / (T2 - T1)
In an ideal operational amplifier depicted below, the potential at node A is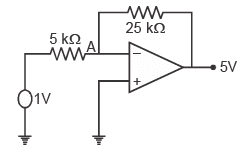
- a)1 V
- b)0 V
- c)5 V
- d)25 V
Correct answer is option 'B'. Can you explain this answer?
In an ideal operational amplifier depicted below, the potential at node A is
a)
1 V
b)
0 V
c)
5 V
d)
25 V
|
Thejas J. answered |
It is the virtual ground concept. For an ideal operational amplifier the voltage on both terminals will be same. Here the non inverting terminal is grounded that the potential will be zero so the potential at A will be zero.
A proton is confined within a nucleus of size 10–13 cm. The uncertainty in its velocity is ________ × 108 m/s.
(Round off to 2 decimal places)
(Planck’s constant h = 6.626 × 10–34 J s and proton mass mp = 1.672 × 10–27 kg)
Correct answer is between '0.3,3.97'. Can you explain this answer?
A proton is confined within a nucleus of size 10–13 cm. The uncertainty in its velocity is ________ × 108 m/s.
(Round off to 2 decimal places)
(Planck’s constant h = 6.626 × 10–34 J s and proton mass mp = 1.672 × 10–27 kg)
(Round off to 2 decimal places)
(Planck’s constant h = 6.626 × 10–34 J s and proton mass mp = 1.672 × 10–27 kg)
|
|
Ameya Rane answered |
^{-15} meters. This means that the proton is located within the nucleus and cannot move freely outside of it. The size of the nucleus is determined by the number of protons and neutrons it contains, which determines its mass and therefore its size. The confinement of the proton within the nucleus is due to the strong nuclear force, which is responsible for holding the protons and neutrons together. This force is much stronger than the electromagnetic force, which would normally cause the protons to repel each other due to their positive charges. The strong nuclear force is also responsible for the process of nuclear fusion, in which two smaller nuclei combine to form a larger nucleus and release energy.
In a typical human body, the amount of radioactive 40K is 3.24 × 10–5 percent of its mass. The activity due to 40K in a human body of mass 70 kg is ________ kBq.
(Round off to 2 decimal places)
(Half-life of 40K = 3.942 × 1016 s, Avogadro’s number NA = 6.022 × 1023 mol–1)
Correct answer is between '5.95,6.01'. Can you explain this answer?
In a typical human body, the amount of radioactive 40K is 3.24 × 10–5 percent of its mass. The activity due to 40K in a human body of mass 70 kg is ________ kBq.
(Round off to 2 decimal places)
(Half-life of 40K = 3.942 × 1016 s, Avogadro’s number NA = 6.022 × 1023 mol–1)
(Round off to 2 decimal places)
(Half-life of 40K = 3.942 × 1016 s, Avogadro’s number NA = 6.022 × 1023 mol–1)
|
Vikram Kapoor answered |
A block of mass 2 kg is at rest on a horizontal table. The coefficient of friction between the block and the table is 0.1. A horizontal force 3 N is applied to the block. The speed of the block (in m/ s) after it has moved a distance 10 m is _______________.
(Specify the answer upto 3 decimal no.)
Correct answer is '3162'. Can you explain this answer?
A block of mass 2 kg is at rest on a horizontal table. The coefficient of friction between the block and the table is 0.1. A horizontal force 3 N is applied to the block. The speed of the block (in m/ s) after it has moved a distance 10 m is _______________.
(Specify the answer upto 3 decimal no.)
(Specify the answer upto 3 decimal no.)
|
Edurev.iitjam answered |
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used is- a)0.01 nm
- b)0.05 nm
- c)0.1 nm
- d)0.15 nm
Correct answer is option 'A'. Can you explain this answer?
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used is
a)
0.01 nm
b)
0.05 nm
c)
0.1 nm
d)
0.15 nm
|
|
Naina Verma answered |
Introduction:
Thermal neutrons are neutrons with low energy, typically around 0.025 electron volts (eV). They are often used in materials science for structural determination, particularly in techniques such as neutron diffraction. The lattice spacing of a material refers to the distance between the repeating units or lattice points in its crystal structure. In this question, we are asked to determine the typical lattice spacing of a material that can be studied using thermal neutrons.
Explanation:
To understand why the correct answer is option 'A' (0.01 nm), let's consider the principles behind neutron diffraction and how it relates to the lattice spacing of a material.
Neutron Diffraction:
Neutron diffraction is a technique used to study the crystal structure of materials. When a beam of neutrons interacts with a crystal, it undergoes scattering due to the interaction with the atomic nuclei in the crystal lattice. This scattering pattern can be analyzed to determine the arrangement of atoms within the crystal.
De Broglie Wavelength:
The scattering of neutrons in a crystal is governed by their de Broglie wavelength, which is given by the equation λ = h/p, where λ is the wavelength, h is the Planck constant, and p is the momentum of the neutron. Since the energy of thermal neutrons is known (0.025 eV), we can use the relation E = p^2/2m, where E is the energy, p is the momentum, and m is the mass of the neutron, to determine the momentum of the neutron.
Determination of Neutron Momentum:
1. Given energy of the thermal neutron: E = 0.025 eV
2. Mass of neutron: m = 1.675 x 10^-27 kg (approximate value)
3. Rearranging the energy equation, we can solve for momentum (p): p^2 = 2mE
4. Plugging in the values, we have: p^2 = 2 * (1.675 x 10^-27 kg) * (0.025 eV)
5. Converting electron volts (eV) to joules (J): 1 eV = 1.602 x 10^-19 J
6. Substituting the values and simplifying, we find: p^2 ≈ 2 * (1.675 x 10^-27 kg) * (0.025 eV) * (1.602 x 10^-19 J/eV)
p^2 ≈ 6.708 x 10^-47 kg·m^2/s^2
Wavelength Calculation:
7. Using the de Broglie wavelength equation, λ = h/p, and substituting the known values, we can calculate the wavelength of the neutron: λ ≈ (6.626 x 10^-34 J·s) / √(6.708 x 10^-47 kg·m^2/s^2)
λ ≈ 1.17 x 10^-10 m
Relationship between Lattice Spacing and Wavelength:
8. In a crystal lattice, the spacing between neighboring lattice points is related to the wavelength of the probing radiation. For constructive interference to occur, the scattering angle must satisfy the Bragg condition:
Thermal neutrons are neutrons with low energy, typically around 0.025 electron volts (eV). They are often used in materials science for structural determination, particularly in techniques such as neutron diffraction. The lattice spacing of a material refers to the distance between the repeating units or lattice points in its crystal structure. In this question, we are asked to determine the typical lattice spacing of a material that can be studied using thermal neutrons.
Explanation:
To understand why the correct answer is option 'A' (0.01 nm), let's consider the principles behind neutron diffraction and how it relates to the lattice spacing of a material.
Neutron Diffraction:
Neutron diffraction is a technique used to study the crystal structure of materials. When a beam of neutrons interacts with a crystal, it undergoes scattering due to the interaction with the atomic nuclei in the crystal lattice. This scattering pattern can be analyzed to determine the arrangement of atoms within the crystal.
De Broglie Wavelength:
The scattering of neutrons in a crystal is governed by their de Broglie wavelength, which is given by the equation λ = h/p, where λ is the wavelength, h is the Planck constant, and p is the momentum of the neutron. Since the energy of thermal neutrons is known (0.025 eV), we can use the relation E = p^2/2m, where E is the energy, p is the momentum, and m is the mass of the neutron, to determine the momentum of the neutron.
Determination of Neutron Momentum:
1. Given energy of the thermal neutron: E = 0.025 eV
2. Mass of neutron: m = 1.675 x 10^-27 kg (approximate value)
3. Rearranging the energy equation, we can solve for momentum (p): p^2 = 2mE
4. Plugging in the values, we have: p^2 = 2 * (1.675 x 10^-27 kg) * (0.025 eV)
5. Converting electron volts (eV) to joules (J): 1 eV = 1.602 x 10^-19 J
6. Substituting the values and simplifying, we find: p^2 ≈ 2 * (1.675 x 10^-27 kg) * (0.025 eV) * (1.602 x 10^-19 J/eV)
p^2 ≈ 6.708 x 10^-47 kg·m^2/s^2
Wavelength Calculation:
7. Using the de Broglie wavelength equation, λ = h/p, and substituting the known values, we can calculate the wavelength of the neutron: λ ≈ (6.626 x 10^-34 J·s) / √(6.708 x 10^-47 kg·m^2/s^2)
λ ≈ 1.17 x 10^-10 m
Relationship between Lattice Spacing and Wavelength:
8. In a crystal lattice, the spacing between neighboring lattice points is related to the wavelength of the probing radiation. For constructive interference to occur, the scattering angle must satisfy the Bragg condition:
A rigid and thermally isolated tank is divided into two compartments of equal volume V, separated by a thin membrane. One compartment contains one mole of an ideal gas A and the other compartment contains one mole of a different ideal gas B. The two gases are in thermal equilibrium at a temperature T. If the membrane ruptures, the two gases mix. Assume that the gases are chemically inert. The change in the total entropy of the gases on mixing is- a)0
- b)R ln 2
- c)3/2R ln 2
- d)2R ln 2
Correct answer is option 'D'. Can you explain this answer?
A rigid and thermally isolated tank is divided into two compartments of equal volume V, separated by a thin membrane. One compartment contains one mole of an ideal gas A and the other compartment contains one mole of a different ideal gas B. The two gases are in thermal equilibrium at a temperature T. If the membrane ruptures, the two gases mix. Assume that the gases are chemically inert. The change in the total entropy of the gases on mixing is
a)
0
b)
R ln 2
c)
3/2R ln 2
d)
2R ln 2
|
|
Ramakrishna Maity answered |
∆smix=nRlnV2/V1 as n =2;V2=2V1 then ∆smix=2Rln2
Chapter doubts & questions for Physics - IIT JAM Past Year Papers and Model Test Paper (All Branches) 2025 is part of IIT JAM exam preparation. The chapters have been prepared according to the IIT JAM exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for IIT JAM 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Physics - IIT JAM Past Year Papers and Model Test Paper (All Branches) in English & Hindi are available as part of IIT JAM exam.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup