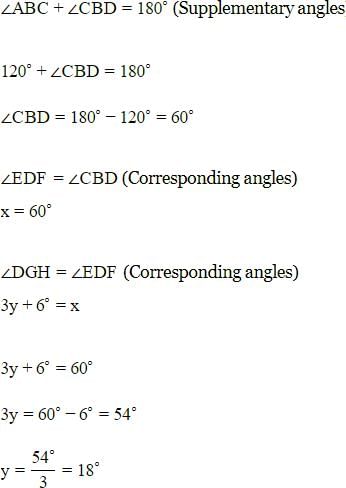All Exams >
UPSC >
CSAT की तैयारी (हिंदी) >
All Questions
All questions of समतल ज्यामिति for UPSC CSE Exam
दो समवृत्त वृत्तों का त्रिज्या 9 सेमी और 15 सेमी है। यदि बड़े वृत्त की तिर्यक छोटी वृत्त के लिए एक स्पर्श रेखा है, तो उस तिर्यक की लंबाई है- a)24 सेंटीमीटर
- b)12 सेमी
- c)30 सेमी
- d)18 सेमी
Correct answer is option 'A'. Can you explain this answer?
दो समवृत्त वृत्तों का त्रिज्या 9 सेमी और 15 सेमी है। यदि बड़े वृत्त की तिर्यक छोटी वृत्त के लिए एक स्पर्श रेखा है, तो उस तिर्यक की लंबाई है
a)
24 सेंटीमीटर
b)
12 सेमी
c)
30 सेमी
d)
18 सेमी

|
Wizius Careers answered |
प्रश्न के अनुसार, हम केंद्र O के साथ एक वृत्त का चित्र बनाते हैं,
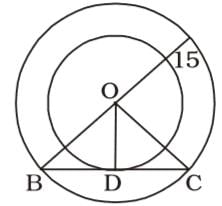
यहाँ, BO = OC = 15 सेमी और OD = 9 सेमी है।
∆ BDO से,

यहाँ, BO = OC = 15 सेमी और OD = 9 सेमी है।
∆ BDO से,
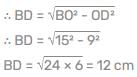
∴ BC = 2 × 12 = 24 सेमी।
दो कोण पूरक हैं और उनके अनुपात 1:4 है। छोटे कोण का मान क्या है?- a)36 डिग्री
- b)45 डिग्री
- c)35 डिग्री
- d)72 डिग्री
Correct answer is option 'A'. Can you explain this answer?
दो कोण पूरक हैं और उनके अनुपात 1:4 है। छोटे कोण का मान क्या है?
a)
36 डिग्री
b)
45 डिग्री
c)
35 डिग्री
d)
72 डिग्री

|
Spectrum Coaching Institute answered |
जैसा कि हम जानते हैं कि कोण पूरक होते हैं, इसलिए कोणों का योग 180 डिग्री होगा।
हम मान लेते हैं कि अनुपात कारक r है।
प्रश्न के अनुसार,
कोण पूरक हैं और उनका अनुपात 1:4 है।
r + 4r = 180
⇒ 5r = 180
⇒ r = 180/5
⇒ r = 36
हम मान लेते हैं कि अनुपात कारक r है।
प्रश्न के अनुसार,
कोण पूरक हैं और उनका अनुपात 1:4 है।
r + 4r = 180
⇒ 5r = 180
⇒ r = 180/5
⇒ r = 36
निम्नलिखित कथनों पर विचार करें: यदि दो सीधी रेखाएँ परस्पर मिलती हैं, तो
I. विपरीत कोण समान होते हैं।
II. विपरीत कोण पूरक होते हैं।
III. निकटवर्ती कोण पूरक होते हैं।
उपरोक्त दिए गए में से कौन सा कथन सही है?- a)केवल III
- b)केवल I
- c)I और III
- d)II और III
Correct answer is option 'B'. Can you explain this answer?
निम्नलिखित कथनों पर विचार करें: यदि दो सीधी रेखाएँ परस्पर मिलती हैं, तो
I. विपरीत कोण समान होते हैं।
II. विपरीत कोण पूरक होते हैं।
III. निकटवर्ती कोण पूरक होते हैं।
उपरोक्त दिए गए में से कौन सा कथन सही है?
I. विपरीत कोण समान होते हैं।
II. विपरीत कोण पूरक होते हैं।
III. निकटवर्ती कोण पूरक होते हैं।
उपरोक्त दिए गए में से कौन सा कथन सही है?
a)
केवल III
b)
केवल I
c)
I और III
d)
II और III

|
Aim It Academy answered |
यहाँ, AB और CD दो रेखाएँ हैं।

यदि दो सीधी रेखाएँ परस्पर मिलती हैं, तो विपरीत कोण समान होते हैं।
इसलिए, विकल्प B सही है।

यदि दो सीधी रेखाएँ परस्पर मिलती हैं, तो विपरीत कोण समान होते हैं।
इसलिए, विकल्प B सही है।
एक चतुर्भुज एक वृत्त में अंकित है। यदि चारों खंडों के बाहर एक कोण अंकित है, तो इन चार कोणों का योग क्या है?- a)270°
- b)360°
- c)540°
- d)720°
Correct answer is option 'C'. Can you explain this answer?
एक चतुर्भुज एक वृत्त में अंकित है। यदि चारों खंडों के बाहर एक कोण अंकित है, तो इन चार कोणों का योग क्या है?
a)
270°
b)
360°
c)
540°
d)
720°

|
Iq Funda answered |
एक चतुर्भुज में अंकित चार कोणों का योग 360° है।

दी गई आकृति में ∠QPR = 90°, QR = 26 सेमी, PM = 6 सेमी, MR = 8 सेमी और ∠PMR = 90°, ΔPQR का क्षेत्रफल ज्ञात करें।
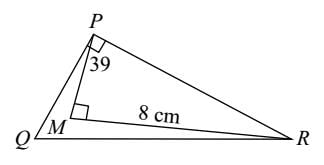
- a)180 सेमी2
- b)240 सेमी2
- c)120 सेमी2
- d)150 सेमी2
Correct answer is option 'C'. Can you explain this answer?
दी गई आकृति में ∠QPR = 90°, QR = 26 सेमी, PM = 6 सेमी, MR = 8 सेमी और ∠PMR = 90°, ΔPQR का क्षेत्रफल ज्ञात करें।


a)
180 सेमी2
b)
240 सेमी2
c)
120 सेमी2
d)
150 सेमी2

|
Aim It Academy answered |
प्रश्न में दिया गया है, QR = 26 सेमी, PM = 6 सेमी, MR = 8 सेमी
प्रश्न के अनुसार, Δ PMR में
(पाइथागोरस का प्रमेय)

प्रश्न के अनुसार, Δ PQR में
(पाइथागोरस का प्रमेय)
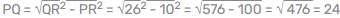
∴ त्रिकोण ∆PQR का क्षेत्रफल = आधार लंबाई x ऊँचाई / 2
⇒ त्रिकोण ∆PQR का क्षेत्रफल = PR x PQ / 2
⇒ त्रिकोण ∆PQR का क्षेत्रफल = 10 x 24 / 2 = 10 x 12
⇒ त्रिकोण ∆PQR का क्षेत्रफल = 120
प्रश्न के अनुसार, Δ PMR में
(पाइथागोरस का प्रमेय)

प्रश्न के अनुसार, Δ PQR में
(पाइथागोरस का प्रमेय)
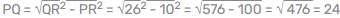
∴ त्रिकोण ∆PQR का क्षेत्रफल = आधार लंबाई x ऊँचाई / 2
⇒ त्रिकोण ∆PQR का क्षेत्रफल = PR x PQ / 2
⇒ त्रिकोण ∆PQR का क्षेत्रफल = 10 x 24 / 2 = 10 x 12
⇒ त्रिकोण ∆PQR का क्षेत्रफल = 120
दो समान त्रिकोणों के क्षेत्रफल 81 cm2 और 144 cm2 हैं। यदि छोटे त्रिकोण की सबसे बड़ी भुजा 27 cm है, तो बड़े त्रिकोण की सबसे बड़ी भुजा होगी:
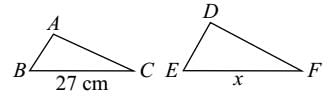
- a)24 सेमी
- b)48 सेमी
- c)36 सेमी
- d)88 सेमी
Correct answer is option 'C'. Can you explain this answer?
दो समान त्रिकोणों के क्षेत्रफल 81 cm2 और 144 cm2 हैं। यदि छोटे त्रिकोण की सबसे बड़ी भुजा 27 cm है, तो बड़े त्रिकोण की सबसे बड़ी भुजा होगी:
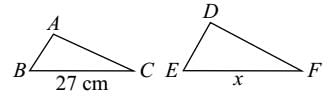
a)
24 सेमी
b)
48 सेमी
c)
36 सेमी
d)
88 सेमी

|
Wizius Careers answered |
मान लें कि ABC और DEF दो समान Δ हैं, जिनका क्षेत्रफल क्रमशः 81 cm2 और 144 cm2 है:
मान लें कि BC = 27 cm
फिर चूंकि ΔABC ∼ ΔDEF
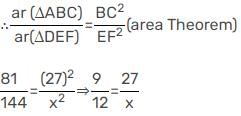
अतः x = 36 cm।
मान लें कि BC = 27 cm
फिर चूंकि ΔABC ∼ ΔDEF
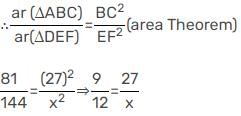
अतः x = 36 cm।
निम्नलिखित आकृति में, दिया गया है कि O वृत्त का केंद्र है और ∠AOC = 140° है। ∠ABC ज्ञात करें।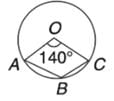
- a)120°
- b)110°
- c)115°
- d)130°
Correct answer is option 'B'. Can you explain this answer?
निम्नलिखित आकृति में, दिया गया है कि O वृत्त का केंद्र है और ∠AOC = 140° है। ∠ABC ज्ञात करें।

a)
120°
b)
110°
c)
115°
d)
130°
|
|
Learnpro Institute answered |
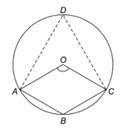
∠AOC का छोटे क्षेत्र का = 140°
∠AOC का बड़े क्षेत्र का = 360° - 140° = 220°
सिद्धांत: केंद्र पर बना कोण वृत्त के परिधि पर बने कोण का दो गुना होता है।
इसलिए,
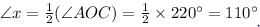
∴ ∠x का मान = 110°
दी गई आकृति में x का मान ज्ञात करें।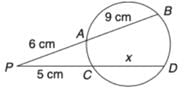
- a)16 सेमी
- b)12 सेंटीमीटर
- c)13 सेंटीमीटर
- d)15 सेंटीमीटर
Correct answer is option 'C'. Can you explain this answer?
दी गई आकृति में x का मान ज्ञात करें।

a)
16 सेमी
b)
12 सेंटीमीटर
c)
13 सेंटीमीटर
d)
15 सेंटीमीटर

|
Glance Learning Institute answered |
तारों के नियम के अनुसार, बाहरी कटाव द्वारा हम प्राप्त करते हैं:
(9 + 6) * 6 = (5 + x) * 5
90 = 25 + 5x
5x = 65
x = 13 सेमी
90 = 25 + 5x
5x = 65
x = 13 सेमी
एक लंबा खड़ा棒, जिसकी लंबाई 20 मीटर है, जमीन पर 10 मीटर लंबी छाया डालता है। उसी समय, एक टॉवर जमीन पर 50 मीटर लंबी छाया डालता है। टॉवर की ऊँचाई ज्ञात करें।- a)80 मीटर
- b)100 मीटर
- c)25 मीटर
- d)200 मीटर
Correct answer is option 'B'. Can you explain this answer?
एक लंबा खड़ा棒, जिसकी लंबाई 20 मीटर है, जमीन पर 10 मीटर लंबी छाया डालता है। उसी समय, एक टॉवर जमीन पर 50 मीटर लंबी छाया डालता है। टॉवर की ऊँचाई ज्ञात करें।
a)
80 मीटर
b)
100 मीटर
c)
25 मीटर
d)
200 मीटर

|
Wizius Careers answered |
जब棒 की लंबाई = 20 मीटर है, तो छाया की लंबाई = 10 मीटर है, अर्थात् इस मामले में लंबाई = 2 * छाया
सूर्य के समान झुकाव के कोण के साथ, टॉवर की लंबाई जो 50 मीटर की छाया डालती है, है: 2 * 50 मीटर = 100 मीटर
टॉवर की ऊँचाई = 100 मीटर
टॉवर की ऊँचाई = 100 मीटर
एक वृत्त की दो तंतु AB और CD, जिसका केंद्र O है, P पर एक-दूसरे को काटते हैं। यदि ∠AOD = 100° और ∠BOC = 70° है, तो ∠APC का मान है- a)80°
- b)75°
- c)85°
- d)95°
Correct answer is option 'D'. Can you explain this answer?
एक वृत्त की दो तंतु AB और CD, जिसका केंद्र O है, P पर एक-दूसरे को काटते हैं। यदि ∠AOD = 100° और ∠BOC = 70° है, तो ∠APC का मान है
a)
80°
b)
75°
c)
85°
d)
95°

|
Wizius Careers answered |
प्रश्न के आधार पर, हम केंद्र O के साथ एक वृत्त का आकृति चित्रित करते हैं,
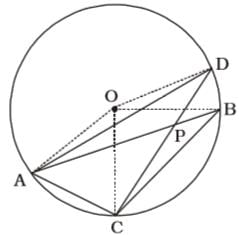
दिया गया है, ∠AOD = 100°
हम जानते हैं कि केंद्र पर बना कोण उस वृत्त पर बने कोण का दुगना होता है जो उसी आर्क द्वारा बनता है।
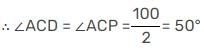
फिर, ∠BOC = 70°
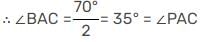
इसलिए, ∠APC = 180° – 50° – 35° = 95°

दिया गया है, ∠AOD = 100°
हम जानते हैं कि केंद्र पर बना कोण उस वृत्त पर बने कोण का दुगना होता है जो उसी आर्क द्वारा बनता है।
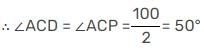
फिर, ∠BOC = 70°
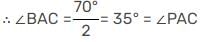
इसलिए, ∠APC = 180° – 50° – 35° = 95°
दी गई आकृति में, AB || CD, ∠ABO = 40° और ∠CDO = 30° है। यदि ∠DOB = x° है, तो x का मान क्या है? 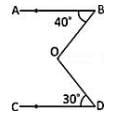
- a)35°
- b)110°
- c)70°
- d)140°
Correct answer is option 'C'. Can you explain this answer?
दी गई आकृति में, AB || CD, ∠ABO = 40° और ∠CDO = 30° है। यदि ∠DOB = x° है, तो x का मान क्या है?

a)
35°
b)
110°
c)
70°
d)
140°
|
|
Learnpro Institute answered |
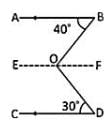
दी गई आकृति में,
O से EOF को AB के समानांतर खींचें और CD के समानांतर भी।
∴ ∠BOF = ∠ABO = 40° (वैकल्पिक कोण)
इसी तरह, ∠FOD = ∠CDO = 30° (वैकल्पिक कोण)
∴ ∠BOD = (40° + 30°) = 70°।
इसलिए, x = 70°।
इसलिए, विकल्प C सही है।
दिए गए चित्र में, AOB एक सीधी रेखा है। यदि ∠AOC + ∠BOD = 85°, तो ∠COD है:
- a)85°
- b)90°
- c)95°
- d)100°
Correct answer is option 'C'. Can you explain this answer?
दिए गए चित्र में, AOB एक सीधी रेखा है। यदि ∠AOC + ∠BOD = 85°, तो ∠COD है:

a)
85°
b)
90°
c)
95°
d)
100°
|
|
Learnpro Institute answered |
स्पष्ट है,
∠AOC + ∠COD + ∠BOD = 180°
∴ 85° + ∠COD = 180°।
इसलिए, ∠COD = (180° - 85°) = 95°।
इसलिए, विकल्प C सही है।
∠AOC + ∠COD + ∠BOD = 180°
∴ 85° + ∠COD = 180°।
इसलिए, ∠COD = (180° - 85°) = 95°।
इसलिए, विकल्प C सही है।
यदि Δ का कोण का द्विभाजक विपरीत भुजा को विभाजित करता है, तो Δ क्या है?- a)स्केलीन
- b)आयताकार
- c)समकोण त्रिकोण
- d)वृत्त
Correct answer is option 'B'. Can you explain this answer?
यदि Δ का कोण का द्विभाजक विपरीत भुजा को विभाजित करता है, तो Δ क्या है?
a)
स्केलीन
b)
आयताकार
c)
समकोण त्रिकोण
d)
वृत्त

|
Glance Learning Institute answered |
चूंकि ∠1 = ∠2
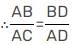
लेकिन BD = CD (दिया गया)
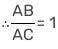
AB = AC
इसलिए, दिया गया ∆ आयताकार है
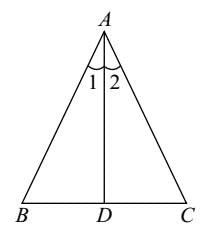
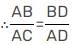
लेकिन BD = CD (दिया गया)
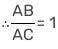
AB = AC
इसलिए, दिया गया ∆ आयताकार है

एक वर्ग को 10 सेमी की त्रिज्या वाले अर्धवृत्त में अंकित किया गया है। अंकित वर्ग का क्षेत्रफल क्या है? (यह मानते हुए कि वर्ग की भुजा अर्धवृत्त के व्यास के साथ है।)- a)70 सेमी2
- b)50 सेमी2
- c)25 सेमी2
- d)80 सेमी2
Correct answer is option 'D'. Can you explain this answer?
एक वर्ग को 10 सेमी की त्रिज्या वाले अर्धवृत्त में अंकित किया गया है। अंकित वर्ग का क्षेत्रफल क्या है? (यह मानते हुए कि वर्ग की भुजा अर्धवृत्त के व्यास के साथ है।)
a)
70 सेमी2
b)
50 सेमी2
c)
25 सेमी2
d)
80 सेमी2

|
Iq Funda answered |
अंकित वर्ग का क्षेत्रफल 50 सेमी2 है।
निम्नलिखित आकृति पर विचार करें: AB = 10 सेमी, AC = 17 सेमी, BC = 21 सेमी और EHFD एक वर्ग है। वर्ग की भुजा की लंबाई (सेमी में) ज्ञात करें।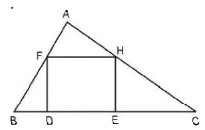
- a)10.5
- b)12
- c)13.5
- d)इनमें से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
निम्नलिखित आकृति पर विचार करें: AB = 10 सेमी, AC = 17 सेमी, BC = 21 सेमी और EHFD एक वर्ग है। वर्ग की भुजा की लंबाई (सेमी में) ज्ञात करें।
a)
10.5
b)
12
c)
13.5
d)
इनमें से कोई नहीं

|
Aim It Academy answered |
वर्ग की भुजा हमेशा त्रिकोण की ऊँचाई से कम होनी चाहिए।
PQRS एक ट्रैपेजियम है, जिसमें PQ RS के समानांतर है, और PQ = 3 (RS)। ट्रैपेजियम का विकर्ण एक-दूसरे को X पर काटता है, तब, ar ( ∆ PXQ) : ar ( ∆ RXS) का अनुपात क्या है?- a)6:1
- b)3:1
- c)9:1
- d)7:1
Correct answer is option 'C'. Can you explain this answer?
PQRS एक ट्रैपेजियम है, जिसमें PQ RS के समानांतर है, और PQ = 3 (RS)। ट्रैपेजियम का विकर्ण एक-दूसरे को X पर काटता है, तब, ar ( ∆ PXQ) : ar ( ∆ RXS) का अनुपात क्या है?
a)
6:1
b)
3:1
c)
9:1
d)
7:1

|
Aim It Academy answered |

∆ PXQ और ∆ RXS में
=> कोण P = कोण R
कोण Q = कोण S
:- ∆ PXQ ~ ∆ RXS ( AA समानता नियम)
ar ( ∆ PXQ) / ar ( ∆ RXS) = ( PQ / RS) ^ 2
= ( 3 / 1 ) ^ 2
= 9 / 1
इसलिए, ar ( ∆ PXQ) : ar ( ∆ RXS)
= 9:1
= 9:1
सबसे बड़ा नियमित षट्कोण H एक समसामिक त्रिकोण X से काटा गया है। सबसे बड़ा समसामिक त्रिकोण Y षट्कोण H से काटा गया है। समसामिक त्रिकोण X और Y के क्षेत्रों का अनुपात क्या है?- a)5 : 1
- b)6 : 1
- c)8 : 1
- d)3 : 1
Correct answer is option 'D'. Can you explain this answer?
सबसे बड़ा नियमित षट्कोण H एक समसामिक त्रिकोण X से काटा गया है। सबसे बड़ा समसामिक त्रिकोण Y षट्कोण H से काटा गया है। समसामिक त्रिकोण X और Y के क्षेत्रों का अनुपात क्या है?
a)
5 : 1
b)
6 : 1
c)
8 : 1
d)
3 : 1

|
Learning Education answered |
समसामिक त्रिकोण X और Y के क्षेत्रों का अनुपात ज्ञात करने के लिए, हमें पहले दोनों त्रिकोणों के क्षेत्रों की गणना करनी होगी।
तीन समान वृत्त एक दूसरे को बाहरी रूप से छूते हैं। यदि इन वृत्तों के केंद्र A, B, C हों, तो ΔABC ________ है।- a)एक समकोण त्रिकोण
- b)एक समभुज त्रिकोण
- c)एक समद्विबाहु त्रिकोण
- d)एक असमभुज त्रिकोण
Correct answer is option 'B'. Can you explain this answer?
तीन समान वृत्त एक दूसरे को बाहरी रूप से छूते हैं। यदि इन वृत्तों के केंद्र A, B, C हों, तो ΔABC ________ है।
a)
एक समकोण त्रिकोण
b)
एक समभुज त्रिकोण
c)
एक समद्विबाहु त्रिकोण
d)
एक असमभुज त्रिकोण

|
Learning Education answered |
चित्र इस प्रकार है:
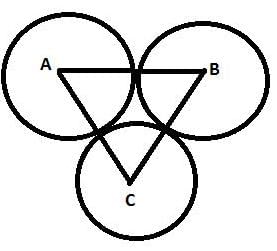
मान लें, वृत्त का त्रिज्या r हो।
तब,
AB = BC = CA = 2r
इसलिए, त्रिकोण के सभी तीन पक्ष समान हैं।
△ABC एक समभुज त्रिकोण है।
इसलिए, आवश्यक उत्तर है समभुज त्रिकोण.

मान लें, वृत्त का त्रिज्या r हो।
तब,
AB = BC = CA = 2r
इसलिए, त्रिकोण के सभी तीन पक्ष समान हैं।
△ABC एक समभुज त्रिकोण है।
इसलिए, आवश्यक उत्तर है समभुज त्रिकोण.
दी गई आकृति में, सीधी रेखाएँ AB और CD O पर मिलती हैं। यदि ∠δ = 3∠v है, तो ∠v = ?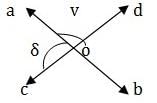
- a)40⁰
- b)50⁰
- c)55⁰
- d)45⁰
Correct answer is option 'D'. Can you explain this answer?
दी गई आकृति में, सीधी रेखाएँ AB और CD O पर मिलती हैं। यदि ∠δ = 3∠v है, तो ∠v = ?

a)
40⁰
b)
50⁰
c)
55⁰
d)
45⁰

|
Wizius Careers answered |
COD एक सीधी रेखा है।
∴ ∠δ + ∠v = 180⁰ ⇒ 3v + v = 180 ⇒ 4v = 180 ⇒ v = 45⁰।
∴ ∠δ + ∠v = 180⁰ ⇒ 3v + v = 180 ⇒ 4v = 180 ⇒ v = 45⁰।
दो सीधे रेखाएँ AB और CD एक दूसरे को O पर काटती हैं। यदि ∠BOD = 63° है, तो ∠BOC क्या होगा?- a)63°
- b)117°
- c)17°
- d)153°
Correct answer is option 'B'. Can you explain this answer?
दो सीधे रेखाएँ AB और CD एक दूसरे को O पर काटती हैं। यदि ∠BOD = 63° है, तो ∠BOC क्या होगा?
a)
63°
b)
117°
c)
17°
d)
153°

|
Spectrum Coaching Institute answered |

जैसा कि दिया गया है ∠BOD = 63°
चूंकि COD एक सीधी रेखा है, हमें यह मिलता है:
∠BOC + ∠BOD = 180°। इसलिए, ∠BOC = (180° ‒ 63°) = 117°।
इसलिए, विकल्प B सही है।
एक पहिया प्रत्येक मिनट में 12 क्रांति करता है। एक सेकंड में पहिये के एक तीर द्वारा वर्णित कोण (रेडियन में) क्या होगा?- a)5π/2
- b)2π/5
- c)3π/5
- d)4π/5
Correct answer is option 'B'. Can you explain this answer?
एक पहिया प्रत्येक मिनट में 12 क्रांति करता है। एक सेकंड में पहिये के एक तीर द्वारा वर्णित कोण (रेडियन में) क्या होगा?
a)
5π/2
b)
2π/5
c)
3π/5
d)
4π/5

|
Wizius Careers answered |
1 मिनट = 60 सेकंड में पहिये द्वारा तय की गई दूरी:
= 12 × उसकी परिधि
= 12 × 2πr
इसलिए 1 सेकंड में पहिये द्वारा तय की गई दूरी
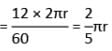
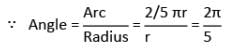
जो आवश्यक कोण है।
इसलिए, विकल्प B सही है।
= 12 × उसकी परिधि
= 12 × 2πr
इसलिए 1 सेकंड में पहिये द्वारा तय की गई दूरी
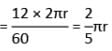
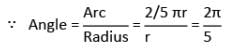
जो आवश्यक कोण है।
इसलिए, विकल्प B सही है।
त्रिकोण का सेंट्रोइड वह बिंदु है जहाँ- a)मध्य रेखाएँ मिलती हैं
- b)ऊँचाइयाँ मिलती हैं
- c)त्रिकोण के भुजाओं के समकोण बिसेक्टर मिलते हैं
- d)त्रिकोण के कोणों के बिसेक्टर मिलते हैं
Correct answer is option 'A'. Can you explain this answer?
त्रिकोण का सेंट्रोइड वह बिंदु है जहाँ
a)
मध्य रेखाएँ मिलती हैं
b)
ऊँचाइयाँ मिलती हैं
c)
त्रिकोण के भुजाओं के समकोण बिसेक्टर मिलते हैं
d)
त्रिकोण के कोणों के बिसेक्टर मिलते हैं

|
Spectrum Coaching Institute answered |
जैसा कि हम जानते हैं, एक त्रिकोण का सेंट्रोइड वह बिंदु है जहाँ त्रिकोण की मध्य रेखाओं का प्रतिच्छेदन होता है।
नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का समाधान करें।
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल के बराबर है। इसके अलावा, वर्ग का परिमाण भी आयत के परिमाण के बराबर है।- a)आयत की चौड़ाई
- b)वर्ग की भुजा
- c)निर्धारित नहीं किया जा सकता
- d)दोनों A और B
Correct answer is option 'D'. Can you explain this answer?
नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का समाधान करें।
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल के बराबर है। इसके अलावा, वर्ग का परिमाण भी आयत के परिमाण के बराबर है।
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल के बराबर है। इसके अलावा, वर्ग का परिमाण भी आयत के परिमाण के बराबर है।
a)
आयत की चौड़ाई
b)
वर्ग की भुजा
c)
निर्धारित नहीं किया जा सकता
d)
दोनों A और B

|
Iq Funda answered |
यह संभव है केवल तब जब आयत की लंबाई और चौड़ाई दोनों वर्ग की भुजा के बराबर हों।
एक ΔABC में, यदि 2∠A = 3∠B = 6∠C है, तो ∠A के बराबर है:- a)60°
- b)30°
- c)90°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
एक ΔABC में, यदि 2∠A = 3∠B = 6∠C है, तो ∠A के बराबर है:
a)
60°
b)
30°
c)
90°
d)
120°

|
Aim It Academy answered |
मान लेते हैं कि 2∠A = 3∠B = 6∠C = K
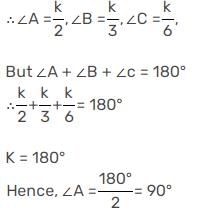
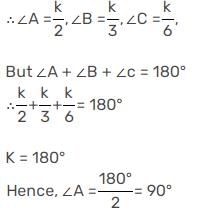
AB वृत्त का व्यास है और ∠PAB=40°
इस स्थिति में ∠PCA का मान क्या है?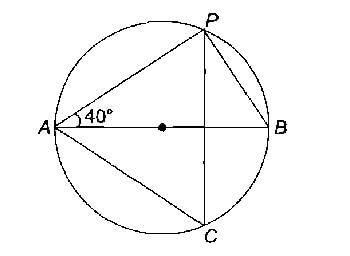
- a)50°
- b)55°
- c)70°
- d)45°
Correct answer is option 'A'. Can you explain this answer?
AB वृत्त का व्यास है और ∠PAB=40°
इस स्थिति में ∠PCA का मान क्या है?
इस स्थिति में ∠PCA का मान क्या है?

a)
50°
b)
55°
c)
70°
d)
45°

|
Glance Learning Institute answered |
समकोण त्रिकोण ΔPAB में
⇒ ∠PAB=40° [ दिया गया ]
⇒ ∠BPA=90° [ अर्धवृत्त में अंकित कोण ]
⇒ ∠PAB + ∠PBA + ∠BPA = 180°
∴ 40° + ∠PBA + 90° = 180°
∴ ∠PBA = 180° - 130°
∴ ∠PBA = 50°
⇒ ∠PBA = ∠PCA = 50° [ एक ही आर्क PA में अंकित कोण ]
∴ ∠PCA = 50°
एक वृत्त त्रिकोण ABC के BC भुजा को P पर छू रहा है और AB और AC भुजाओं को क्रमशः Q और R पर छू रहा है। यदि AQ = 6 सेमी है, तो त्रिकोण ABC का परिमाप क्या है?- a)6 सेमी
- b)10 सेमी
- c)12 सेमी
- d)18 सेमी
Correct answer is option 'C'. Can you explain this answer?
एक वृत्त त्रिकोण ABC के BC भुजा को P पर छू रहा है और AB और AC भुजाओं को क्रमशः Q और R पर छू रहा है। यदि AQ = 6 सेमी है, तो त्रिकोण ABC का परिमाप क्या है?
a)
6 सेमी
b)
10 सेमी
c)
12 सेमी
d)
18 सेमी

|
Learning Education answered |
एक वृत्त AQ और AR भुजाओं को छू रहा है,

फिर AR = AQ = 6 सेमी
अब AQ + AR = AB + BQ + AC + CR
⇒ 6 + 6 = AB + BQ + AC + CR
⇒ 6 + 6 = AB + BQ + AC + CR
[यहाँ BQ = BP और CR = CP]
12 = AB + AC + BP + PC
12 = AB + AC + BC
इसलिए, त्रिकोण ABC का परिमाप 12 सेमी है।

फिर AR = AQ = 6 सेमी
अब AQ + AR = AB + BQ + AC + CR
⇒ 6 + 6 = AB + BQ + AC + CR
⇒ 6 + 6 = AB + BQ + AC + CR
[यहाँ BQ = BP और CR = CP]
12 = AB + AC + BP + PC
12 = AB + AC + BC
इसलिए, त्रिकोण ABC का परिमाप 12 सेमी है।
रेखा AB की लंबाई 6 मीटर है और यह दो समांतर वृत्तों के बीच के आंतरिक वृत्त पर बिंदु C पर स्पर्श करती है। यह ज्ञात है कि दोनों वृत्तों की त्रिज्याएँ पूर्णांक हैं। बाहरी वृत्त की त्रिज्या क्या है, जहाँ A और B बाहरी वृत्त पर बिंदु हैं?- a)5 मीटर
- b)4 मीटर
- c)6 मीटर
- d)3 मीटर
Correct answer is option 'A'. Can you explain this answer?
रेखा AB की लंबाई 6 मीटर है और यह दो समांतर वृत्तों के बीच के आंतरिक वृत्त पर बिंदु C पर स्पर्श करती है। यह ज्ञात है कि दोनों वृत्तों की त्रिज्याएँ पूर्णांक हैं। बाहरी वृत्त की त्रिज्या क्या है, जहाँ A और B बाहरी वृत्त पर बिंदु हैं?
a)
5 मीटर
b)
4 मीटर
c)
6 मीटर
d)
3 मीटर

|
T.S Academy answered |
आइए आंतरिक वृत्त की त्रिज्या को r1 और बाहरी वृत्त की त्रिज्या को r2 मान लें। बाहरी वृत्त से आंतरिक वृत्त तक के स्पर्श की लंबाई इस प्रकार दी जाती है:
AC2 = AB2 - (r2 - r1)2
यह ज्ञात है कि AB = 6 मीटर है, और रेखा AB बिंदु C पर आंतरिक वृत्त को स्पर्श करती है, पायथागोरस के प्रमेय द्वारा:
r22 = r12 + 32
चूँकि त्रिज्याएँ पूर्णांक हैं, इसे हल करने से हमें r1 = 3 मीटर और r2 = 5 मीटर मिलता है। इसलिए, बाहरी वृत्त की त्रिज्या 5 मीटर है।
AC2 = AB2 - (r2 - r1)2
यह ज्ञात है कि AB = 6 मीटर है, और रेखा AB बिंदु C पर आंतरिक वृत्त को स्पर्श करती है, पायथागोरस के प्रमेय द्वारा:
r22 = r12 + 32
चूँकि त्रिज्याएँ पूर्णांक हैं, इसे हल करने से हमें r1 = 3 मीटर और r2 = 5 मीटर मिलता है। इसलिए, बाहरी वृत्त की त्रिज्या 5 मीटर है।
वह त्रिकोण जिसका दो मध्य 9 सेमी और 12 सेमी लंबे हैं, उनके बीच समकोण पर मिलन बिंदु है, उसका क्षेत्रफल क्या है?- a)72
- b)60
- c)56
- d)48
Correct answer is option 'A'. Can you explain this answer?
वह त्रिकोण जिसका दो मध्य 9 सेमी और 12 सेमी लंबे हैं, उनके बीच समकोण पर मिलन बिंदु है, उसका क्षेत्रफल क्या है?
a)
72
b)
60
c)
56
d)
48

|
Learning Education answered |
त्रिकोण का क्षेत्रफल 72 सेमी² है, जो उस त्रिकोण के दो मध्य के समकोण पर मिलने के कारण निकाला गया है।
एक वृत्त जिसका व्यास 10 सेमी है, उसे केंद्र से 12 सेमी की ऊँचाई पर छह समान तंकों द्वारा लटकाया गया है। तंकों को वृत्त के परिधि पर समान अंतराल पर जोड़ा गया है, जिससे वृत्त एक क्षैतिज तल में बना रहता है। दो निकटतम तंकों के बीच के कोण का कोसाइन मान किस सीमा में है?- a)0 और 1/2
- b)1/2 और 1
- c)- 1 / 2 से 0
- d)- 1 से - 1 / 2
Correct answer is option 'B'. Can you explain this answer?
एक वृत्त जिसका व्यास 10 सेमी है, उसे केंद्र से 12 सेमी की ऊँचाई पर छह समान तंकों द्वारा लटकाया गया है। तंकों को वृत्त के परिधि पर समान अंतराल पर जोड़ा गया है, जिससे वृत्त एक क्षैतिज तल में बना रहता है। दो निकटतम तंकों के बीच के कोण का कोसाइन मान किस सीमा में है?
a)
0 और 1/2
b)
1/2 और 1
c)
- 1 / 2 से 0
d)
- 1 से - 1 / 2

|
Aim It Academy answered |
समस्या को एक नियमित षट्भुज के आधार के रूप में एक पिरामिड के रूप में विचार करें।
अब A POR में
अब A POR में
OP = 12 सेमी
OR = 5 सेमी
PR = 13 सेमी
अब कोसाइन सूत्र उत्तर देगा।
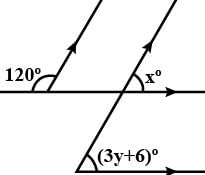
नीचे दिए गए चित्र में, AB, CD के समानांतर है। ∠ABC = 65°, ∠CDE = 15° और AB = AE है। ∠AEF का मान क्या है?

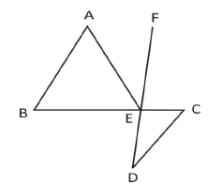
- a)30°
- b)35°
- c)40°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
नीचे दिए गए चित्र में, AB, CD के समानांतर है। ∠ABC = 65°, ∠CDE = 15° और AB = AE है। ∠AEF का मान क्या है?


a)
30°
b)
35°
c)
40°
d)
45°

|
Spectrum Coaching Institute answered |
दी गई जानकारी के अनुसार,
∠ABC = 65° और ∠CDE = 15°
यहाँ, ∠ABC + ∠TCB = 180° (∵ AB || CD)
∠TCB = 180° – ∠ABC
∴ ∠TCB = 180° – 65° = 115°
∵ ∠TCB + ∠DCB = 180° (रेखीय जोड़ी)
∴ ∠DCB = 65°
अब, ΔCDE में
∠CED = 180° – (∠ECD + ∠EDC) (∵ ∠ECD = ∠BCD)
= 180° – (– 65° + 15°) = 100°
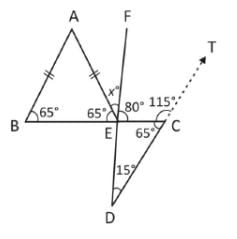
∵ ∠DEC + ∠FEC = 180°
⇒ ∠FEC = 180° – 100° = 80°
दी गई जानकारी के अनुसार, AB = AE। अर्थात् ΔABE एक समद्विबाहु त्रिकोण है।
∴ ∠ABE = ∠AEB = 65°
∵ ∠AEB + ∠AEF + ∠FEC = 180° (स्ट्रेट लाइन)
⇒ 65° + x° + 80° = 180°
∴ x° = 180° – 145° = 35°।
इसलिए, विकल्प B सही है।
∠ABC = 65° और ∠CDE = 15°
यहाँ, ∠ABC + ∠TCB = 180° (∵ AB || CD)
∠TCB = 180° – ∠ABC
∴ ∠TCB = 180° – 65° = 115°
∵ ∠TCB + ∠DCB = 180° (रेखीय जोड़ी)
∴ ∠DCB = 65°
अब, ΔCDE में
∠CED = 180° – (∠ECD + ∠EDC) (∵ ∠ECD = ∠BCD)
= 180° – (– 65° + 15°) = 100°

∵ ∠DEC + ∠FEC = 180°
⇒ ∠FEC = 180° – 100° = 80°
दी गई जानकारी के अनुसार, AB = AE। अर्थात् ΔABE एक समद्विबाहु त्रिकोण है।
∴ ∠ABE = ∠AEB = 65°
∵ ∠AEB + ∠AEF + ∠FEC = 180° (स्ट्रेट लाइन)
⇒ 65° + x° + 80° = 180°
∴ x° = 180° – 145° = 35°।
इसलिए, विकल्प B सही है।
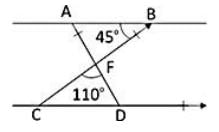
दी गई आकृति में, AB || CD, m∠ABF = 45° और m∠CFC = 110° है। तब, m∠FDC है:
- a)25°
- b)45°
- c)35°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
दी गई आकृति में, AB || CD, m∠ABF = 45° और m∠CFC = 110° है। तब, m∠FDC है:


a)
25°
b)
45°
c)
35°
d)
30°
|
|
Learnpro Institute answered |
दी गई आकृति में,
∴∠FCD = ∠FBA = 45° (वैकल्पिक ∠s)
∠FDC = 180° ‒ (110° + 45°) = 25°
इसलिए, विकल्प A सही है।
∴∠FCD = ∠FBA = 45° (वैकल्पिक ∠s)
∠FDC = 180° ‒ (110° + 45°) = 25°
इसलिए, विकल्प A सही है।
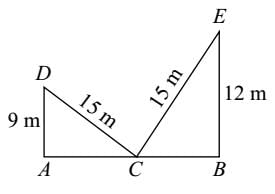
एक 15 मीटर लंबी सीढ़ी एक खिड़की तक पहुँचती है जो सड़क के एक तरफ जमीन से 9 मीटर ऊँची है। इसके पैर को उसी स्थान पर रखते हुए, सीढ़ी को सड़क के दूसरी तरफ घुमाया जाता है ताकि यह 12 मीटर ऊँची खिड़की तक पहुँच सके। सड़क की चौड़ाई क्या है:- a)31 मीटर
- b)12 मीटर
- c)30 मीटर
- d)21 मीटर
Correct answer is option 'D'. Can you explain this answer?
एक 15 मीटर लंबी सीढ़ी एक खिड़की तक पहुँचती है जो सड़क के एक तरफ जमीन से 9 मीटर ऊँची है। इसके पैर को उसी स्थान पर रखते हुए, सीढ़ी को सड़क के दूसरी तरफ घुमाया जाता है ताकि यह 12 मीटर ऊँची खिड़की तक पहुँच सके। सड़क की चौड़ाई क्या है:
a)
31 मीटर
b)
12 मीटर
c)
30 मीटर
d)
21 मीटर

|
Wizius Careers answered |
दिए गए प्रश्न के अनुसार एक चित्र बनाएं,
एक समकोण त्रिकोण ADC में, (पाइथागोरस प्रमेय) का उपयोग करें

एक समकोण त्रिकोण BCE में, सूत्र का उपयोग करें

इसलिए; सड़क की चौड़ाई (AC + BC) = AB = 12 + 9 = 21 मीटर।

एक समकोण त्रिकोण ADC में, (पाइथागोरस प्रमेय) का उपयोग करें
एक समकोण त्रिकोण BCE में, सूत्र का उपयोग करें
इसलिए; सड़क की चौड़ाई (AC + BC) = AB = 12 + 9 = 21 मीटर।

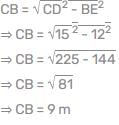
चित्र में x का मान ज्ञात कीजिए, यदि यह दिया गया है कि AC और BD वृत्त के व्यास हैं।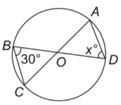
- a)60°
- b)30°
- c)15°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
चित्र में x का मान ज्ञात कीजिए, यदि यह दिया गया है कि AC और BD वृत्त के व्यास हैं।

a)
60°
b)
30°
c)
15°
d)
45°

|
Target Study Academy answered |
त्रिकोण BOC एक समद्विबाहु त्रिकोण है जिसमें OB और OC की भुजाएं समान हैं क्योंकि वे वृत्त के त्रिज्याएँ हैं। इसलिए, कोण OBC = कोण OCB = 30°।
अतः त्रिकोण BOC का तीसरा कोण यानी कोण BOC 120° के बराबर होगा।
⇒ BOC = AOD = 120°
⇒ BOC = AOD = 120°
इसके अलावा, समद्विबाहु त्रिकोण DOA में:
कोण ODA = कोण DAO = x = 30°
कोण ODA = कोण DAO = x = 30°
नीचे दिए गए चित्र में, PQ = QS, QR = RS और कोण SRQ = 100° है। कोण QPS कितने डिग्री का है?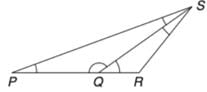
- a)30°
- b)15°
- c)40°
- d)20°
Correct answer is option 'D'. Can you explain this answer?
नीचे दिए गए चित्र में, PQ = QS, QR = RS और कोण SRQ = 100° है। कोण QPS कितने डिग्री का है?

a)
30°
b)
15°
c)
40°
d)
20°
|
|
Learnpro Institute answered |
में ΔQRS, QR = RS
⇒ ㄥRQS = ㄥRSQ (क्योंकि समान भुजाओं के सामने वाले कोण समान होते हैं)।
इस प्रकार:
⇒ ㄥRQS = ㄥRSQ (क्योंकि समान भुजाओं के सामने वाले कोण समान होते हैं)।
इस प्रकार:
ㄥRQS + ㄥRSQ = 180° - 100° = 80°
ㄥRQS = ㄥRSQ = 40°
ㄥPQS = 180° – 40° = 140° (एक रेखा पर कोणों का योग = 180°)
ㄥRQS = ㄥRSQ = 40°
ㄥPQS = 180° – 40° = 140° (एक रेखा पर कोणों का योग = 180°)
फिर, ㄥQPS = ㄥQSP (चूंकि समान भुजाओं के सामने वाले कोण समान होते हैं)
ㄥQPS + ㄥQSP = 180° – 140° = 40°
ㄥQPS = ㄥQSP = 20°
ㄥQPS = ㄥQSP = 20°
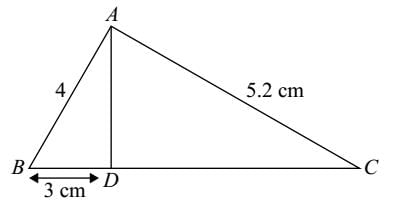
दी गई आकृति में ∠BAD = ∠CAD है। AB = 4 सेमी, AC = 5.2 सेमी, BD = 3 सेमी है। BC ज्ञात करें।
- a)6.9 सेमी
- b)9.6 सेमी
- c)3.9 सेमी
- d)9.3 सेमी
Correct answer is option 'A'. Can you explain this answer?
दी गई आकृति में ∠BAD = ∠CAD है। AB = 4 सेमी, AC = 5.2 सेमी, BD = 3 सेमी है। BC ज्ञात करें।


a)
6.9 सेमी
b)
9.6 सेमी
c)
3.9 सेमी
d)
9.3 सेमी
|
|
Learnpro Institute answered |
प्रश्न के अनुसार, दिया गया है कि
∠BAD = ∠CAD है। AB = 4 सेमी, AC = 5.2 सेमी, BD = 3 सेमी
ΔABC में, AD ∠A का बाइसेक्टर है।

लेकिन BC = BD + CD = 3 सेमी + 3.9 सेमी = 6.9 सेमी है।
∠BAD = ∠CAD है। AB = 4 सेमी, AC = 5.2 सेमी, BD = 3 सेमी
ΔABC में, AD ∠A का बाइसेक्टर है।

लेकिन BC = BD + CD = 3 सेमी + 3.9 सेमी = 6.9 सेमी है।
एक त्रिकोण की दो भुजाएँ 4 और 5 हैं। फिर, त्रिकोण के क्षेत्रफल के लिए, निम्नलिखित में से कौन सा सीमा सबसे तीव्र है?- a)<10.
- b)≤ 10.
- c)< 8.
- d)> 5.
Correct answer is option 'B'. Can you explain this answer?
एक त्रिकोण की दो भुजाएँ 4 और 5 हैं। फिर, त्रिकोण के क्षेत्रफल के लिए, निम्नलिखित में से कौन सा सीमा सबसे तीव्र है?
a)
<10.
b)
≤ 10.
c)
< 8.
d)
> 5.
|
|
Learnpro Institute answered |
मान लीजिए AB = 4 और BC = 5 है और AB, BC पर लंबवत है।
फिर क्षेत्रफल = 1/2 AB . AC = 1/2 . 4.5 = 10
सन्निहित चित्र में, ∠ABC = 100°, ∠EDC = 120° और AB || DE है। तब, ∠BCD के मान के बराबर है: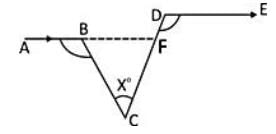
- a)80°
- b)60°
- c)40°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
सन्निहित चित्र में, ∠ABC = 100°, ∠EDC = 120° और AB || DE है। तब, ∠BCD के मान के बराबर है:

a)
80°
b)
60°
c)
40°
d)
20°

|
Wizius Careers answered |
दिए गए चित्र में,
AB को CD पर F पर मिलने के लिए बढ़ाएं।
∠BFD = ∠EDF = 120° (वैकल्पिक ∠)
∠BFC = (180° ‒ 120°) = 60°।
∠CBF = (180° ‒ 100°) = 80°.
इसलिए, ∠BCF = 180° ‒ (60° + 80°) = 40°।
इसलिए, विकल्प C सही है।
AB को CD पर F पर मिलने के लिए बढ़ाएं।
∠BFD = ∠EDF = 120° (वैकल्पिक ∠)
∠BFC = (180° ‒ 120°) = 60°।
∠CBF = (180° ‒ 100°) = 80°.
इसलिए, ∠BCF = 180° ‒ (60° + 80°) = 40°।
इसलिए, विकल्प C सही है।
यदि कोणों का मापन (5y + 62°) और (22° + y) पूरक हैं, तो y का मान होगा:- a)16°
- b)32°
- c)8°
- d)1°
Correct answer is option 'A'. Can you explain this answer?
यदि कोणों का मापन (5y + 62°) और (22° + y) पूरक हैं, तो y का मान होगा:
a)
16°
b)
32°
c)
8°
d)
1°

|
Wizius Careers answered |
जैसा कि हम जानते हैं कि दो पूरक कोणों का योग = 180°
इसलिए, (5y + 62°) + (22° + y) = 180°
⇒ 6y + 84° = 180°
⇒ 6y = 180° – 84° = 96°
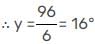
इसलिए, (5y + 62°) + (22° + y) = 180°
⇒ 6y + 84° = 180°
⇒ 6y = 180° – 84° = 96°
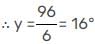
ΔABC में, D और E क्रमशः AB और AC के मध्य बिंदु हैं। ΔADE और ΔABC के क्षेत्रफल का अनुपात ज्ञात कीजिये।- a)1/2
- b)1/4
- c)3/4
- d)1/8
Correct answer is option 'B'. Can you explain this answer?
ΔABC में, D और E क्रमशः AB और AC के मध्य बिंदु हैं। ΔADE और ΔABC के क्षेत्रफल का अनुपात ज्ञात कीजिये।
a)
1/2
b)
1/4
c)
3/4
d)
1/8
|
|
Learnpro Institute answered |
स्पष्ट रूप से DE || BC (BPT के विपरीत) और इसलिए ΔADE ∼ ABC (∠A = ∠A और ∠ADE = ∠B)


दी गई आकृति में, ∠B = ∠C = 55° और ∠D = 25° है। तब: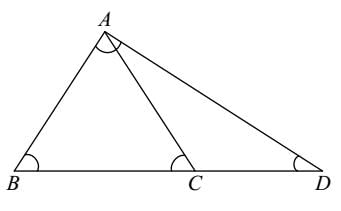
- a)BC < ca=""><>
- b)BC > CA > CD
- c)BC < ca,="" ca=""> CD
- d)बीसी > सीए, सीए <>
Correct answer is option 'D'. Can you explain this answer?
दी गई आकृति में, ∠B = ∠C = 55° और ∠D = 25° है। तब:

a)
BC < ca=""><>
b)
BC > CA > CD
c)
BC < ca,="" ca=""> CD
d)
बीसी > सीए, सीए <>

|
Aim It Academy answered |
प्रश्न के अनुसार,
∠B = ∠C = 55° , ∠D = 25°
हम कह सकते हैं ,
AB = AC ( ∴ ∠B = ∠C = 55° )
त्रिभुज ABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 55° + 55° = 180°
⇒ ∠A + 110° = 180°
⇒ ∠A = 180° - 110°
⇒ ∠A = 70° ..........................(1)
दी गई आकृति के अनुसार,
∠ACD + ∠ACB = 180° ( ∠ACB = ∠C = 55°)
⇒ ∠ACD + 55° = 180°
⇒ ∠ACD = 180° - 55°
⇒ ∠ACD = 125° ....................... (2)
अब त्रिभुज ACD में,
∠CAD + ∠ACD + ∠CDA = 180°
⇒ ∠CAD + 125° + 25° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30° ...........................(3)
( एक Δ में, बड़ा कोण उसके विपरीत लंबाई में बड़ी भुजा होती है )
समीकरण (1), (2) और (3) से;
∠B < ∠A और ∠CAD > ∠D ;
∴ BC > CA और CA < CD
∠B = ∠C = 55° , ∠D = 25°
हम कह सकते हैं ,
AB = AC ( ∴ ∠B = ∠C = 55° )
त्रिभुज ABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 55° + 55° = 180°
⇒ ∠A + 110° = 180°
⇒ ∠A = 180° - 110°
⇒ ∠A = 70° ..........................(1)
दी गई आकृति के अनुसार,
∠ACD + ∠ACB = 180° ( ∠ACB = ∠C = 55°)
⇒ ∠ACD + 55° = 180°
⇒ ∠ACD = 180° - 55°
⇒ ∠ACD = 125° ....................... (2)
अब त्रिभुज ACD में,
∠CAD + ∠ACD + ∠CDA = 180°
⇒ ∠CAD + 125° + 25° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30° ...........................(3)
( एक Δ में, बड़ा कोण उसके विपरीत लंबाई में बड़ी भुजा होती है )
समीकरण (1), (2) और (3) से;
∠B < ∠A और ∠CAD > ∠D ;
∴ BC > CA और CA < CD
दी गई आकृति में, यदि AB || CD है, तो ∠FXE के बराबर है:

- a)30°
- b)50°
- c)70°
- d)80°
Correct answer is option 'D'. Can you explain this answer?
दी गई आकृति में, यदि AB || CD है, तो ∠FXE के बराबर है:

a)
30°
b)
50°
c)
70°
d)
80°

|
Aim It Academy answered |
दिए गए चित्र के अनुसार,
∠BFE = ∠CEF = 110° (वैकल्पिक ∠s).
इसलिए, ∠XFE = ∠BFE ‒ ∠BFX = (110° ‒ 50°) = 60°.
और सीधी रेखा CD पर,
110° + ∠FEX + 30° = 180° ⇒ ∠FEX = 40°.
अब, ∠XFE + ∠FEX + ∠FXE = 180° ⇒ 60° + 40° + ∠FXE = 180°.
इसलिए, ∠FXE = 80°.
अतः, विकल्प D सही है.
∠BFE = ∠CEF = 110° (वैकल्पिक ∠s).
इसलिए, ∠XFE = ∠BFE ‒ ∠BFX = (110° ‒ 50°) = 60°.
और सीधी रेखा CD पर,
110° + ∠FEX + 30° = 180° ⇒ ∠FEX = 40°.
अब, ∠XFE + ∠FEX + ∠FXE = 180° ⇒ 60° + 40° + ∠FXE = 180°.
इसलिए, ∠FXE = 80°.
अतः, विकल्प D सही है.
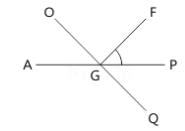
दी गई आकृति में रेखाएँ AP और OQ बिंदु G पर मिलती हैं। यदि ∠AGO + ∠PGF = 70° और ∠PGQ = 40° है, तो ∠PGF का कोण मान ज्ञात करें।
- a)31°
- b)35°
- c)30°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
दी गई आकृति में रेखाएँ AP और OQ बिंदु G पर मिलती हैं। यदि ∠AGO + ∠PGF = 70° और ∠PGQ = 40° है, तो ∠PGF का कोण मान ज्ञात करें।


a)
31°
b)
35°
c)
30°
d)
20°

|
Spectrum Coaching Institute answered |
चूँकि, AP एक सीधी रेखा है और किरणें GO और GF इस पर स्थित हैं।
इसलिए, ∠AGO + ∠OGF + ∠PGF = 180°
⇒ (∠AGO + ∠PGE) + ∠OGF = 180°
⇒ 70° + ∠OGF = 180°
⇒ ∠OGF = 180° – 70°
⇒ ∠OGF = 110°
चूँकि, OQ एक सीधी रेखा है, किरणें GF और GP इस पर स्थित हैं।
∠OGF + ∠PGF + ∠PGQ = 180°
∠OGF और ∠PGQ का मान रखते हुए
110° + ∠PGF + 40° = 180°
∠PGF = 180° – 150° = 30°
इसलिए, विकल्प C सही है।
इसलिए, ∠AGO + ∠OGF + ∠PGF = 180°
⇒ (∠AGO + ∠PGE) + ∠OGF = 180°
⇒ 70° + ∠OGF = 180°
⇒ ∠OGF = 180° – 70°
⇒ ∠OGF = 110°
चूँकि, OQ एक सीधी रेखा है, किरणें GF और GP इस पर स्थित हैं।
∠OGF + ∠PGF + ∠PGQ = 180°
∠OGF और ∠PGQ का मान रखते हुए
110° + ∠PGF + 40° = 180°
∠PGF = 180° – 150° = 30°
इसलिए, विकल्प C सही है।
80° का पूरक कोण क्या है?- a)

- b)
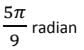
- c)

- d)
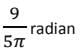
Correct answer is option 'C'. Can you explain this answer?
80° का पूरक कोण क्या है?
a)

b)
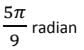
c)

d)
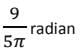

|
Learning Education answered |
पूरक कोण: पूरक कोण वे कोण जो मिलकर एक समकोण (90°) बनाते हैं।
इसलिए, आवश्यक कोण 10° होगा।
180° = π रेडियन
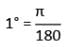
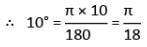
इसलिए, विकल्प C सही है।
इसलिए, आवश्यक कोण 10° होगा।
180° = π रेडियन
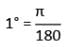
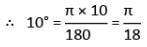
इसलिए, विकल्प C सही है।
यदि दो कोण एक-दूसरे के पूरक हैं, तो प्रत्येक कोण क्या है?
- a)एक obtuse कोण
- b)एक सही कोण
- c)एक acute कोण
- d)एक पूरक कोण
Correct answer is option 'C'. Can you explain this answer?
यदि दो कोण एक-दूसरे के पूरक हैं, तो प्रत्येक कोण क्या है?

a)
एक obtuse कोण
b)
एक सही कोण
c)
एक acute कोण
d)
एक पूरक कोण

|
Aim It Academy answered |
यदि दो कोण पूरक हैं, तो स्पष्ट रूप से प्रत्येक कोण 90° से कम है और इसलिए यह एक acute कोण है।
इसलिए, विकल्प C सही है।
इसलिए, विकल्प C सही है।
दो गोलों के केंद्रों के बीच की दूरी, जिनकी त्रिज्याएँ r1 और r2 हैं, d है। यदि ये एक-दूसरे को आंतरिक रूप से छूएँगे तो- a)d = r1 या r2
- b)d = r1 + r2
- c)d = r1 - r2
- d)उपरोक्त में से कोई नहीं
Correct answer is option 'C'. Can you explain this answer?
दो गोलों के केंद्रों के बीच की दूरी, जिनकी त्रिज्याएँ r1 और r2 हैं, d है। यदि ये एक-दूसरे को आंतरिक रूप से छूएँगे तो
a)
d = r1 या r2
b)
d = r1 + r2
c)
d = r1 - r2
d)
उपरोक्त में से कोई नहीं
|
|
Learnpro Institute answered |
प्रश्न के अनुसार, हम एक चित्र बना सकते हैं
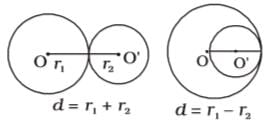
इसलिए, विकल्प C सही उत्तर है।

इसलिए, विकल्प C सही उत्तर है।
Chapter doubts & questions for समतल ज्यामिति - CSAT की तैयारी (हिंदी) 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of समतल ज्यामिति - CSAT की तैयारी (हिंदी) in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup