All Exams >
UPSC >
CSAT की तैयारी (हिंदी) >
All Questions
All questions of मापन: आयतन, सतही क्षेत्र और ठोस आकृतियाँ for UPSC CSE Exam
एक शंकु के फलक का ऊँचाई 8 सेमी है। फलक के शीर्ष का व्यास 6 सेमी और फलक के आधार का व्यास 12 सेमी है। फलक का घुमावदार क्षेत्रफल क्या होगा?- a)240π सेमी2
- b)180π सेमी2
- c)360π सेमी2
- d)उपरोक्त में से एक से अधिक
Correct answer is option 'B'. Can you explain this answer?
एक शंकु के फलक का ऊँचाई 8 सेमी है। फलक के शीर्ष का व्यास 6 सेमी और फलक के आधार का व्यास 12 सेमी है। फलक का घुमावदार क्षेत्रफल क्या होगा?
a)
240π सेमी2
b)
180π सेमी2
c)
360π सेमी2
d)
उपरोक्त में से एक से अधिक

|
Learning Education answered |
दिया गया:
फलक के आधार का व्यास = 12 सेमी।
फलक के शीर्ष का व्यास = 6 सेमी।
ऊँचाई = 8 सेमी
फलक के शीर्ष का व्यास = 6 सेमी।
ऊँचाई = 8 सेमी
उपयोग में लाया गया सूत्र:
एक शंकु के फलक की तिरछी ऊँचाई,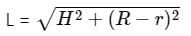
एक शंकु के फलक का घुमावदार क्षेत्रफल, CSA = π × L(R + r)
जहाँ फलक के आधार का व्यास = R, फलक के शीर्ष का व्यास = r, ऊँचाई = H, और तिरछी ऊँचाई = L
एक शंकु के फलक की तिरछी ऊँचाई,
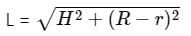
एक शंकु के फलक का घुमावदार क्षेत्रफल, CSA = π × L(R + r)
जहाँ फलक के आधार का व्यास = R, फलक के शीर्ष का व्यास = r, ऊँचाई = H, और तिरछी ऊँचाई = L
गणना:
इसलिए, एक शंकु के फलक की तिरछी ऊँचाई, L
इसलिए, एक शंकु के फलक की तिरछी ऊँचाई, L
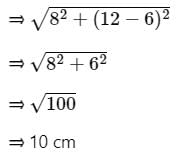
इस प्रकार, एक शंकु के फलक का घुमावदार क्षेत्रफल, CSA
⇒ π x 10 x (12 + 6)
⇒ π x 10 x 18
⇒ 180π सेमी2
⇒ π x 10 x (12 + 6)
⇒ π x 10 x 18
⇒ 180π सेमी2
∴ फलक का घुमावदार क्षेत्रफल 180π सेमी2 है।
एक कोन का कुल सतही क्षेत्रफल क्या है, जिसका व्यास 10 सेमी है और ऊँचाई 24 सेमी है?- a)1376.73 सेमी2
- b)1131.43 सेमी2
- c)1249.37 सेमी2
- d)उपरोक्त में से एक से अधिक
Correct answer is option 'B'. Can you explain this answer?
एक कोन का कुल सतही क्षेत्रफल क्या है, जिसका व्यास 10 सेमी है और ऊँचाई 24 सेमी है?
a)
1376.73 सेमी2
b)
1131.43 सेमी2
c)
1249.37 सेमी2
d)
उपरोक्त में से एक से अधिक

|
Wizius Careers answered |
दी गई जानकारी:
कोन का व्यास = 10 सेमी
कोन की ऊँचाई = 24 सेमी
सूत्र:
कोन का कुल सतही क्षेत्रफल = πR(L + R)


जहाँ, R = आधार का व्यास, H = कोन की ऊँचाई,
L = कोन की तिरछी ऊँचाई
गणना:

कोन का कुल सतही क्षेत्रफल

कोन का कुल सतही क्षेत्रफल
⇒ π x 10 x (26 + 10)
⇒ 22/7 x 10 x 36
⇒ 7920/7 = 1131.428 ≈ 1131.43 सेमी2
∴ कोन का कुल सतही क्षेत्रफल 1131.43 सेमी2 है।
एक आयताकार क्षेत्र की लंबाई 100 मीटर और चौड़ाई 40 मीटर है। क्षेत्रफल क्या होगा?- a)(4 x 102) वर्ग मीटर
- b)(4 x 10) वर्ग मीटर
- c)(4 x 104) वर्ग मीटर
- d)(4 x 103) वर्ग मीटर
Correct answer is option 'D'. Can you explain this answer?
एक आयताकार क्षेत्र की लंबाई 100 मीटर और चौड़ाई 40 मीटर है। क्षेत्रफल क्या होगा?
a)
(4 x 102) वर्ग मीटर
b)
(4 x 10) वर्ग मीटर
c)
(4 x 104) वर्ग मीटर
d)
(4 x 103) वर्ग मीटर

|
Iq Funda answered |
आवश्यक क्षेत्रफल = लंबाई x चौड़ाई
= 100 x 40 = 4000 वर्ग मीटर
= 4 x 103 वर्ग मीटर
= 100 x 40 = 4000 वर्ग मीटर
= 4 x 103 वर्ग मीटर
यदि एक वर्ग की भुजा में 4 सेमी की वृद्धि की जाती है, तो क्षेत्रफल 60 वर्ग सेमी बढ़ जाता है। वर्ग की भुजा क्या है?- a)12 सेमी
- b)13 सेमी
- c)14 सेमी
- d)इनमें से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
यदि एक वर्ग की भुजा में 4 सेमी की वृद्धि की जाती है, तो क्षेत्रफल 60 वर्ग सेमी बढ़ जाता है। वर्ग की भुजा क्या है?
a)
12 सेमी
b)
13 सेमी
c)
14 सेमी
d)
इनमें से कोई नहीं

|
Glance Learning Institute answered |
मान लेते हैं कि प्रत्येक भुजा = x सेमी है।
फिर, (x + 4 )2 - x2 = 60
⇒ x 2 + 8x + 16 - x2 = 60
∴ x = 5.5 सेमी
फिर, (x + 4 )2 - x2 = 60
⇒ x 2 + 8x + 16 - x2 = 60
∴ x = 5.5 सेमी
यदि एक अर्धगोलाकार का व्यास 28 सेमी है, तो अर्धगोलाकार का आयतन क्या होगा?- a)5749.33 सेमी3
- b)6349.22 सेमी3
- c)6728.11 सेमी3
- d)5124.44 सेमी3
Correct answer is option 'A'. Can you explain this answer?
यदि एक अर्धगोलाकार का व्यास 28 सेमी है, तो अर्धगोलाकार का आयतन क्या होगा?
a)
5749.33 सेमी3
b)
6349.22 सेमी3
c)
6728.11 सेमी3
d)
5124.44 सेमी3

|
Aim It Academy answered |
दी गई:
एक अर्धगोल का व्यास 28 सेमी है।
उपयोग किया गया सिद्धांत:
1. अर्धगोल का आयतन = 2πR3/3 (जहां R = त्रिज्या)
2. व्यास = त्रिज्या × 2
2. व्यास = त्रिज्या × 2
गणना:
अर्धगोल की त्रिज्या = 28/2 = 14 सेमी
अब, अर्धगोल का आयतन
अब, अर्धगोल का आयतन

∴ अर्धगोल का आयतन 5749.33 सेमी3 है।
28 सेमी ऊँचाई और 10 सेमी त्रिज्या वाले एक बेलन को पिघलाकर 4 वर्ग आधार वाले पिरामिडों में ढाला गया है, जिनकी ऊँचाई H समान है और प्रत्येक पिरामिड का आधार लंबाई समान है। यदि पिरामिड के आधार की लंबाई 20 सेमी है, तो पिरामिड की ऊँचाई ज्ञात कीजिए।- a)8.25 सेंटीमीटर
- b)16.5 सेमी
- c)33 सेंटीमीटर
- d)5.5 सेमी
Correct answer is option 'B'. Can you explain this answer?
28 सेमी ऊँचाई और 10 सेमी त्रिज्या वाले एक बेलन को पिघलाकर 4 वर्ग आधार वाले पिरामिडों में ढाला गया है, जिनकी ऊँचाई H समान है और प्रत्येक पिरामिड का आधार लंबाई समान है। यदि पिरामिड के आधार की लंबाई 20 सेमी है, तो पिरामिड की ऊँचाई ज्ञात कीजिए।
a)
8.25 सेंटीमीटर
b)
16.5 सेमी
c)
33 सेंटीमीटर
d)
5.5 सेमी

|
Iq Funda answered |
सिलेंडर की ऊँचाई = 28 सेमी
सिलेंडर का व्यास = 10 सेमी
सिलेंडर का आयतन = πr2h
⇒ 22/7 x 28 x 10 x 10
⇒ 8800 सेमी3
अब सिलेंडर को पिघलाकर समान आयतन के 4 पिरामिडों में ढाला जाता है।
प्रत्येक पिरामिड का आयतन = 8800/4 = 2200 सेमी3
पिरामिड का आयतन = (आधार का क्षेत्रफल x ऊँचाई)/3
पिरामिड के आधार की लंबाई = 20 सेमी
पिरामिड के आधार का क्षेत्रफल = 20 x 20 = 400 सेमी2
⇒ 1/3 x H x 400 = 2200
⇒ H = 16.5 सेमी
सिलेंडर का व्यास = 10 सेमी
सिलेंडर का आयतन = πr2h
⇒ 22/7 x 28 x 10 x 10
⇒ 8800 सेमी3
अब सिलेंडर को पिघलाकर समान आयतन के 4 पिरामिडों में ढाला जाता है।
प्रत्येक पिरामिड का आयतन = 8800/4 = 2200 सेमी3
पिरामिड का आयतन = (आधार का क्षेत्रफल x ऊँचाई)/3
पिरामिड के आधार की लंबाई = 20 सेमी
पिरामिड के आधार का क्षेत्रफल = 20 x 20 = 400 सेमी2
⇒ 1/3 x H x 400 = 2200
⇒ H = 16.5 सेमी
एक सही पिरामिड का आधार एक वर्ग है और वर्ग की भुजा की लंबाई 32 सेंटीमीटर है तथा पिरामिड की ऊँचाई 12 सेंटीमीटर है, तो वर्ग पिरामिड का कुल सतही क्षेत्रफल क्या होगा?- a)2114 वर्ग सेमी
- b)2304 वर्ग सेंटीमीटर
- c)2204 वर्ग सेंटीमीटर
- d)2314 वर्ग सेंटीमीटर
Correct answer is option 'B'. Can you explain this answer?
एक सही पिरामिड का आधार एक वर्ग है और वर्ग की भुजा की लंबाई 32 सेंटीमीटर है तथा पिरामिड की ऊँचाई 12 सेंटीमीटर है, तो वर्ग पिरामिड का कुल सतही क्षेत्रफल क्या होगा?
a)
2114 वर्ग सेमी
b)
2304 वर्ग सेंटीमीटर
c)
2204 वर्ग सेंटीमीटर
d)
2314 वर्ग सेंटीमीटर

|
Target Study Academy answered |
दी गई जानकारी:
एक समकोणीय पिरामिड का आधार एक वर्ग है और वर्ग की भुजा की लंबाई 32 सेमी है।
पिरामिड की ऊँचाई 12 सेमी है।
पिरामिड की ऊँचाई 12 सेमी है।
उपयोग किया गया सूत्र:
कुल सतह क्षेत्र = पार्श्व सतह क्षेत्र + आधार का क्षेत्र
पार्श्व सतह क्षेत्र = 1/2 × आधार की परिधि × तिरछी ऊँचाई
पार्श्व सतह क्षेत्र = 1/2 × आधार की परिधि × तिरछी ऊँचाई
गणना:

ΔOAB में
तिरछी ऊँचाई, l

अब, कुल सतह क्षेत्र = पार्श्व सतह क्षेत्र + आधार का क्षेत्र
⇒ 1/2 × आधार की परिधि × तिरछी ऊँचाई + आधार का क्षेत्र
⇒ 1/2 × (4 × 32) × 20 + (32)2
⇒ 1280 + 1024
⇒ 2304 वर्ग सेमी
⇒ 1/2 × आधार की परिधि × तिरछी ऊँचाई + आधार का क्षेत्र
⇒ 1/2 × (4 × 32) × 20 + (32)2
⇒ 1280 + 1024
⇒ 2304 वर्ग सेमी
27 सेमी ऊँचाई वाले समभुज त्रिकोण का क्षेत्रफल क्या है?- a)213√3 सेमी2
- b)256√3 सेमी2
- c)243√3 सेमी2
- d)343√3 सेमी2
Correct answer is option 'C'. Can you explain this answer?
27 सेमी ऊँचाई वाले समभुज त्रिकोण का क्षेत्रफल क्या है?
a)
213√3 सेमी2
b)
256√3 सेमी2
c)
243√3 सेमी2
d)
343√3 सेमी2

|
Aim It Academy answered |
समभुज त्रिकोण का क्षेत्रफल

इसलिए, विकल्प C सही है।

इसलिए, विकल्प C सही है।
अनिल अपने पिछवाड़े में टमाटर उगाते हैं, जिसका आकार चौकोर है। प्रत्येक टमाटर के लिए उनके पिछवाड़े में 1 सेमी2 स्थान लगता है। इस वर्ष, वह पिछले वर्ष की तुलना में 131 अधिक टमाटर उगाने में सक्षम रहे हैं। पिछवाड़े का आकार चौकोर ही रहा। इस वर्ष अनिल ने कितने टमाटर उत्पन्न किए?- a)4225
- b)4096
- c)4356
- d)अपर्याप्त डेटा
Correct answer is option 'C'. Can you explain this answer?
अनिल अपने पिछवाड़े में टमाटर उगाते हैं, जिसका आकार चौकोर है। प्रत्येक टमाटर के लिए उनके पिछवाड़े में 1 सेमी2 स्थान लगता है। इस वर्ष, वह पिछले वर्ष की तुलना में 131 अधिक टमाटर उगाने में सक्षम रहे हैं। पिछवाड़े का आकार चौकोर ही रहा। इस वर्ष अनिल ने कितने टमाटर उत्पन्न किए?
a)
4225
b)
4096
c)
4356
d)
अपर्याप्त डेटा

|
Aim It Academy answered |
इस वर्ष पिछवाड़े का क्षेत्रफल x2 मान लें और पिछले वर्ष का क्षेत्रफल y2 मान लें।
X2 - Y2 = 131
(X+Y) (X-Y) = 131
(X+Y) (X-Y) = 131
अब, 131 एक असामान्य संख्या है (यह एक अद्वितीय संख्या भी है। इसके गुणों की जानकारी गूगल पर देखें)। साथ ही, प्रश्न में दिए गए असामान्य संख्या को हमेशा पहचानें। यह समाधान को हल करने में मददगार हो सकता है।
⇒ (X+Y) (X-Y) = 131 x 1
⇒ X+Y = 131
⇒ X-Y = 1
⇒ 2X = 132
⇒ X = 66 और Y = 65
⇒ X+Y = 131
⇒ X-Y = 1
⇒ 2X = 132
⇒ X = 66 और Y = 65
∴ इस वर्ष उत्पादित टमाटरों की संख्या = 662 = 4356
इसलिए विकल्प (C) सही उत्तर है।
सही उत्तर: 4356
इसलिए विकल्प (C) सही उत्तर है।
सही उत्तर: 4356
एक क्यूबॉइड के आकार 15 मीटर x 20 मीटर x 18 मीटर को अंदर और बाहर से 5 पैसे प्रति वर्ग मीटर की दर से रंगा गया। यदि क्यूबॉइड धातु का बना है जिसका मोटाई नगण्य है, तो क्यूबॉइड को अंदर और बाहर रंगने के लिए कितने पैसे (रुपयों में) की आवश्यकता होगी?- a)9300
- b)93
- c)186
- d)18600
Correct answer is option 'C'. Can you explain this answer?
एक क्यूबॉइड के आकार 15 मीटर x 20 मीटर x 18 मीटर को अंदर और बाहर से 5 पैसे प्रति वर्ग मीटर की दर से रंगा गया। यदि क्यूबॉइड धातु का बना है जिसका मोटाई नगण्य है, तो क्यूबॉइड को अंदर और बाहर रंगने के लिए कितने पैसे (रुपयों में) की आवश्यकता होगी?
a)
9300
b)
93
c)
186
d)
18600

|
T.S Academy answered |
क्यूबॉइड का कुल सतह क्षेत्रफल = 2(लंबाई x चौड़ाई + चौड़ाई x ऊँचाई + ऊँचाई x लंबाई) = 2(15 x 20 + 20 x 18 + 18 x 15) = 2 x (300 +
360 + 270) = 2 x 930 = 1860 वर्ग मीटर
क्यूबॉइड धातु का बना है जिसका मोटाई नगण्य है, तो बाहरी सतह क्षेत्र = आंतरिक सतह क्षेत्र
आवश्यक उत्तर = 2 x 1860 x 5 = 18600 पैसे = 186 रुपये
इसलिए, विकल्प C सही है।
360 + 270) = 2 x 930 = 1860 वर्ग मीटर
क्यूबॉइड धातु का बना है जिसका मोटाई नगण्य है, तो बाहरी सतह क्षेत्र = आंतरिक सतह क्षेत्र
आवश्यक उत्तर = 2 x 1860 x 5 = 18600 पैसे = 186 रुपये
इसलिए, विकल्प C सही है।
एक आयत के अंदर सबसे बड़े वर्ग का क्षेत्रफल क्या है, जिसकी लंबाई 10 मीटर और चौड़ाई 4 मीटर है?- a)10 मीटर2
- b)12 मीटर2
- c)14 मीटर2
- d)16 मीटर2
Correct answer is option 'D'. Can you explain this answer?
एक आयत के अंदर सबसे बड़े वर्ग का क्षेत्रफल क्या है, जिसकी लंबाई 10 मीटर और चौड़ाई 4 मीटर है?
a)
10 मीटर2
b)
12 मीटर2
c)
14 मीटर2
d)
16 मीटर2

|
Learning Education answered |
वर्ग की भुजा आयत की चौड़ाई के समान होनी चाहिए।
वर्ग की भुजा = 4 मीटर
इसलिए उत्तर = 4 × 4 = 16 मीटर2
इसलिए, विकल्प D सही है।
वर्ग की भुजा = 4 मीटर
इसलिए उत्तर = 4 × 4 = 16 मीटर2
इसलिए, विकल्प D सही है।
एक त्रिकोण का क्षेत्रफल ज्ञात करें जिसकी आधार 4 सेमी और ऊँचाई 6 सेमी है।- a)10 सेमी2
- b)14 सेमी2
- c)16 सेमी2
- d)12 सेमी2
Correct answer is option 'D'. Can you explain this answer?
एक त्रिकोण का क्षेत्रफल ज्ञात करें जिसकी आधार 4 सेमी और ऊँचाई 6 सेमी है।
a)
10 सेमी2
b)
14 सेमी2
c)
16 सेमी2
d)
12 सेमी2

|
Iq Funda answered |
हमें पता है कि त्रिकोण का क्षेत्रफल 1/2 आधार × ऊँचाई के बराबर होता है।
यहाँ, आधार = 4 सेमी और ऊँचाई = 6 सेमी है।
इसलिए, क्षेत्रफल = 1/2 × 4 × 6 = 24 /2 = 12 सेमी2 है।
यहाँ, आधार = 4 सेमी और ऊँचाई = 6 सेमी है।
इसलिए, क्षेत्रफल = 1/2 × 4 × 6 = 24 /2 = 12 सेमी2 है।
16 मीटर किनारे वाले घन का आयतन क्या है?- a)3,600 m3
- b)3,750 m3
- c)3,900 m3
- d)4,096 m3
Correct answer is option 'D'. Can you explain this answer?
16 मीटर किनारे वाले घन का आयतन क्या है?
a)
3,600 m3
b)
3,750 m3
c)
3,900 m3
d)
4,096 m3

|
Learning Education answered |
घन का आयतन = किनारा3
इसलिए उत्तर = 16 × 16 × 16 = 4,096 m3
इसलिए, विकल्प D सही है।
इसलिए उत्तर = 16 × 16 × 16 = 4,096 m3
इसलिए, विकल्प D सही है।
यदि वर्ग का क्षेत्रफल 256 सेमी2 है और आयत की चौड़ाई वर्ग के पक्ष से 20% अधिक है और लंबाई 50% अधिक है, तो वर्ग के क्षेत्रफल और आयत के क्षेत्रफल का अनुपात ज्ञात करें।- a)4 : 5
- b)3 : 4
- c)3 : 7
- d)5 : 9
Correct answer is option 'D'. Can you explain this answer?
यदि वर्ग का क्षेत्रफल 256 सेमी2 है और आयत की चौड़ाई वर्ग के पक्ष से 20% अधिक है और लंबाई 50% अधिक है, तो वर्ग के क्षेत्रफल और आयत के क्षेत्रफल का अनुपात ज्ञात करें।
a)
4 : 5
b)
3 : 4
c)
3 : 7
d)
5 : 9

|
Target Study Academy answered |
वर्ग का क्षेत्रफल = 256 सेमी2, वर्ग का पक्ष = 16 सेमी
आयत का क्षेत्रफल = लंबाई x चौड़ाई
लंबाई = 16 x 1.5 = 24 सेमी
चौड़ाई = 16 x 1.2 = 19.2 सेमी
आयत का क्षेत्रफल = 460.8 सेमी2
आयत का क्षेत्रफल = लंबाई x चौड़ाई
लंबाई = 16 x 1.5 = 24 सेमी
चौड़ाई = 16 x 1.2 = 19.2 सेमी
आयत का क्षेत्रफल = 460.8 सेमी2

इसलिए, विकल्प D सही है।
ABCD एक वर्ग है जो PTRS नामक वर्ग के अंदर खींचा गया है, जिसकी भुजाएँ 4 सेमी हैं, PR, PT, TS, SR के मध्य बिंदुओं को जोड़कर। इसी तरह से ABCD के अंदर एक और वर्ग खींचा गया है। यह प्रक्रिया अनंत बार दोहराई जाती है। सभी वर्गों का योग ज्ञात करें।- a)16 सेमी2
- b)28 सेमी2
- c)32 सेमी2
- d)अनंत
Correct answer is option 'C'. Can you explain this answer?
ABCD एक वर्ग है जो PTRS नामक वर्ग के अंदर खींचा गया है, जिसकी भुजाएँ 4 सेमी हैं, PR, PT, TS, SR के मध्य बिंदुओं को जोड़कर। इसी तरह से ABCD के अंदर एक और वर्ग खींचा गया है। यह प्रक्रिया अनंत बार दोहराई जाती है। सभी वर्गों का योग ज्ञात करें।
a)
16 सेमी2
b)
28 सेमी2
c)
32 सेमी2
d)
अनंत

|
T.S Academy answered |
यदि हम वर्गों के क्षेत्रफल की अनंत श्रृंखला लिखें:
= 42 + (2√2)2 + 22 + ……. अनंत
चूंकि यह एक घटती श्रृंखला है, अनंत पदों का योग अनुमानित किया जा सकता है।
= 16 + 8 + 4 +………अनंत
एक आयताकार कमरे की लंबाई और चौड़ाई का अनुपात 3 : 4 है। कमरे में फर्श पर रखने के लिए सबसे लंबी डंडी की लंबाई 25 सेमी है। कमरे के फर्श को सीमेंट करने की कुल लागत प्रति वर्ग सेमी 5 रुपये की दर से क्या होगी?- a)रु. 1200
- b)रु. 1500
- c)रु. 960
- d)रु. 1800
Correct answer is option 'B'. Can you explain this answer?
एक आयताकार कमरे की लंबाई और चौड़ाई का अनुपात 3 : 4 है। कमरे में फर्श पर रखने के लिए सबसे लंबी डंडी की लंबाई 25 सेमी है। कमरे के फर्श को सीमेंट करने की कुल लागत प्रति वर्ग सेमी 5 रुपये की दर से क्या होगी?
a)
रु. 1200
b)
रु. 1500
c)
रु. 960
d)
रु. 1800

|
Spectrum Coaching Institute answered |
कमरे में फर्श पर रखने के लिए सबसे लंबी डंडी की लंबाई वास्तव में आयत का विकर्ण है।
इसलिए, पायथागोरस के प्रमेय से,
(3x)2 + (4x)2 = 252
जहाँ 3x कमरे की लंबाई है और 4x कमरे की चौड़ाई है।
9x2 + 16x2 = 625
हल करने पर, x = 5 सेमी
कमरे के फर्श का क्षेत्रफल = 3x x 4x = 12 x 5 x 5 = 300 वर्ग सेमी
कमरे के फर्श को सीमेंट करने की कुल लागत = 5 x 300 = रु. 1500
इसलिए, विकल्प B सही है।
इसलिए, पायथागोरस के प्रमेय से,
(3x)2 + (4x)2 = 252
जहाँ 3x कमरे की लंबाई है और 4x कमरे की चौड़ाई है।
9x2 + 16x2 = 625
हल करने पर, x = 5 सेमी
कमरे के फर्श का क्षेत्रफल = 3x x 4x = 12 x 5 x 5 = 300 वर्ग सेमी
कमरे के फर्श को सीमेंट करने की कुल लागत = 5 x 300 = रु. 1500
इसलिए, विकल्प B सही है।
जिसका भुजा 8 सेमी है, उस समभुज त्रिकोण का क्षेत्रफल क्या है?- a)64 सेमी2
- b)16√3 सेमी2
- c)21.3 सेमी2
- d)4√3 सेमी2
Correct answer is option 'B'. Can you explain this answer?
जिसका भुजा 8 सेमी है, उस समभुज त्रिकोण का क्षेत्रफल क्या है?
a)
64 सेमी2
b)
16√3 सेमी2
c)
21.3 सेमी2
d)
4√3 सेमी2

|
Aim It Academy answered |
आवश्यक क्षेत्रफल = √3/4 × a2 = √3/4 × 82 सेमी2
= 16√3 सेमी2
= 16√3 सेमी2
यदि एक आयत के किनारों को 10% बढ़ाया जाए तो इसके विकर्णों में कितने प्रतिशत की वृद्धि होगी?- a)20%
- b)10%
- c)15%
- d)18%
Correct answer is option 'B'. Can you explain this answer?
यदि एक आयत के किनारों को 10% बढ़ाया जाए तो इसके विकर्णों में कितने प्रतिशत की वृद्धि होगी?
a)
20%
b)
10%
c)
15%
d)
18%

|
Wizius Careers answered |
सूत्र के अनुसार,
∵ किनारों में प्रतिशत वृद्धि = 10%
∴ विकर्णों में प्रतिशत वृद्धि = 10%
∵ किनारों में प्रतिशत वृद्धि = 10%
∴ विकर्णों में प्रतिशत वृद्धि = 10%
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल से 28 वर्ग सेंटीमीटर अधिक है, जिसकी लंबाई 14 सेंटीमीटर और चौड़ाई 12 सेंटीमीटर है। वर्ग के अंतर्गत वृत्त का क्षेत्रफल क्या होगा?- a)162 वर्ग सेंटीमीटर।
- b)154 वर्ग सेंटीमीटर।
- c)132 वर्ग सेंटीमीटर।
- d)160 वर्ग सेंटीमीटर।
Correct answer is option 'B'. Can you explain this answer?
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल से 28 वर्ग सेंटीमीटर अधिक है, जिसकी लंबाई 14 सेंटीमीटर और चौड़ाई 12 सेंटीमीटर है। वर्ग के अंतर्गत वृत्त का क्षेत्रफल क्या होगा?
a)
162 वर्ग सेंटीमीटर।
b)
154 वर्ग सेंटीमीटर।
c)
132 वर्ग सेंटीमीटर।
d)
160 वर्ग सेंटीमीटर।

|
Wizius Careers answered |
आयत का क्षेत्रफल = लंबाई × चौड़ाई = 14 × 12 = 168 वर्ग सेंटीमीटर
वर्ग का क्षेत्रफल = 168 + 28 = 196 वर्ग सेंटीमीटर
वर्ग की भुजा = 196 का वर्गमूल = 14 सेंटीमीटर
वर्ग के अंतर्गत वृत्त का त्रिज्या

आवश्यक क्षेत्रफल
वर्ग का क्षेत्रफल = 168 + 28 = 196 वर्ग सेंटीमीटर
वर्ग की भुजा = 196 का वर्गमूल = 14 सेंटीमीटर
वर्ग के अंतर्गत वृत्त का त्रिज्या

आवश्यक क्षेत्रफल

इसलिए, विकल्प B सही है।
14 सेमी त्रिज्या वाले अर्धवृत्त का परिमाप क्या है?- a)60 सेमी
- b)64 सेमी
- c)70 सेमी
- d)72 सेमी
Correct answer is option 'D'. Can you explain this answer?
14 सेमी त्रिज्या वाले अर्धवृत्त का परिमाप क्या है?
a)
60 सेमी
b)
64 सेमी
c)
70 सेमी
d)
72 सेमी

|
Spectrum Coaching Institute answered |
अर्धवृत्त का परिमाप = πr + 2r
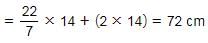
इसलिए, विकल्प D सही है।
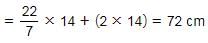
इसलिए, विकल्प D सही है।
एक वर्ग का परिमाप एक आयत के परिमाप का दो गुना है। यदि वर्ग का परिमाप 72 सेमी है और आयत की लंबाई उसकी चौड़ाई से 2 सेमी अधिक है, तो आयत की चौड़ाई क्या है?- a)8 सेमी
- b)10 सेमी
- c)12 सेमी
- d)15 सेमी
Correct answer is option 'A'. Can you explain this answer?
एक वर्ग का परिमाप एक आयत के परिमाप का दो गुना है। यदि वर्ग का परिमाप 72 सेमी है और आयत की लंबाई उसकी चौड़ाई से 2 सेमी अधिक है, तो आयत की चौड़ाई क्या है?
a)
8 सेमी
b)
10 सेमी
c)
12 सेमी
d)
15 सेमी

|
Learning Education answered |
आयत का परिमाप
= 72/2 = 36 सेमी
मान लीजिए कि आयत की चौड़ाई = x
लंबाई = x + 2
2 × (x + x + 2) = 36
2x + 2 = 18
x = 8 सेमी
इसलिए, विकल्प A सही है।
= 72/2 = 36 सेमी
मान लीजिए कि आयत की चौड़ाई = x
लंबाई = x + 2
2 × (x + x + 2) = 36
2x + 2 = 18
x = 8 सेमी
इसलिए, विकल्प A सही है।
समद्विबाहु त्रिकोण की ऊँचाई 2 √ 3 सेंटीमीटर है?- a)√ 3/2 सेंटीमीटर
- b)1/2 सेंटीमीटर
- c)√ 3/4
- d)3 सेंटीमीटर
Correct answer is option 'D'. Can you explain this answer?
समद्विबाहु त्रिकोण की ऊँचाई 2 √ 3 सेंटीमीटर है?
a)
√ 3/2 सेंटीमीटर
b)
1/2 सेंटीमीटर
c)
√ 3/4
d)
3 सेंटीमीटर

|
Target Study Academy answered |
∵ 1/2 x 2 √ x h
= √3/4 x (2 √3)2
∴ h = 3 सेंटीमीटर।
= √3/4 x (2 √3)2
∴ h = 3 सेंटीमीटर।
यदि एक आयत की लंबाई 25% बढ़ाई जाती है और चौड़ाई 33.33% घटाई जाती है, तो इसके विकर्ण पर क्या प्रभाव पड़ेगा (लगभग)?- a)7.6%
- b)8.33%
- c)6%
- d)7.33%
Correct answer is option 'A'. Can you explain this answer?
यदि एक आयत की लंबाई 25% बढ़ाई जाती है और चौड़ाई 33.33% घटाई जाती है, तो इसके विकर्ण पर क्या प्रभाव पड़ेगा (लगभग)?
a)
7.6%
b)
8.33%
c)
6%
d)
7.33%

|
Spectrum Coaching Institute answered |
मान लें कि आयत की लंबाई = 4 इकाइयाँ
और आयत की चौड़ाई = 3 इकाइयाँ
तब आयत का विकर्ण = √(42 + 32) = 5 इकाइयाँ
प्रश्न के अनुसार, आयत की लंबाई 25% बढ़ाई जाती है और चौड़ाई को 33.33% घटाया जाता है
नई लंबाई = 4 इकाइयों का 125% = 5 इकाइयाँ
नई चौड़ाई = 3 इकाइयों का 66.66% = 2 इकाइयाँ
नई आयत में, नया विकर्ण = √(52 + 22) = √29 = लगभग 5.38 इकाइयाँ
और आयत की चौड़ाई = 3 इकाइयाँ
तब आयत का विकर्ण = √(42 + 32) = 5 इकाइयाँ
प्रश्न के अनुसार, आयत की लंबाई 25% बढ़ाई जाती है और चौड़ाई को 33.33% घटाया जाता है
नई लंबाई = 4 इकाइयों का 125% = 5 इकाइयाँ
नई चौड़ाई = 3 इकाइयों का 66.66% = 2 इकाइयाँ
नई आयत में, नया विकर्ण = √(52 + 22) = √29 = लगभग 5.38 इकाइयाँ

इसलिए, विकल्प A सही है।
हॉल की लंबाई उसकी चौड़ाई के (4/3) गुना है। यदि हॉल का क्षेत्रफल 300 वर्ग मीटर है, तो लंबाई और चौड़ाई के बीच का अंतर क्या है?- a)15 मीटर
- b)4 मीटर
- c)3 मीटर
- d)इनमें से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
हॉल की लंबाई उसकी चौड़ाई के (4/3) गुना है। यदि हॉल का क्षेत्रफल 300 वर्ग मीटर है, तो लंबाई और चौड़ाई के बीच का अंतर क्या है?
a)
15 मीटर
b)
4 मीटर
c)
3 मीटर
d)
इनमें से कोई नहीं

|
Learning Education answered |
मान लें चौड़ाई = b मीटर।
फिर, लंबाई = 4b/3 मीटर।
∵ b x 4b/3 = 300
फिर, लंबाई = 4b/3 मीटर।
∵ b x 4b/3 = 300
⇒ b2 = 300 x 3/4
⇒ b2 = 225
∴ b = 15
⇒ b2 = 225
∴ b = 15
इसलिए, आवश्यक अंतर = [(लंबाई) - (चौड़ाई)]
= 4b/3 - b
= b/3
= 15/3 मीटर
= 5 मीटर
= 4b/3 - b
= b/3
= 15/3 मीटर
= 5 मीटर
एक समकोण त्रिकोणीय प्रिज्म की पार्श्व सतह क्षेत्रफल 288 cm2 है। यदि छोटे आधारों की लंबाई क्रमशः 6 cm और 8 cm है, तो प्रिज्म की ऊँचाई ज्ञात करें।- a)14 सेंटीमीटर
- b)12 सेमी
- c)24 सेमी
- d)22 सेंटीमीटर
Correct answer is option 'B'. Can you explain this answer?
एक समकोण त्रिकोणीय प्रिज्म की पार्श्व सतह क्षेत्रफल 288 cm2 है। यदि छोटे आधारों की लंबाई क्रमशः 6 cm और 8 cm है, तो प्रिज्म की ऊँचाई ज्ञात करें।
a)
14 सेंटीमीटर
b)
12 सेमी
c)
24 सेमी
d)
22 सेंटीमीटर

|
Glance Learning Institute answered |
बड़े आधार की लंबाई = √(62 + 82) = 10 सेमी (पाइथागोरस के प्रमेय का उपयोग करते हुए)
मान लें कि प्रिज्म की ऊँचाई की लंबाई X सेमी है।
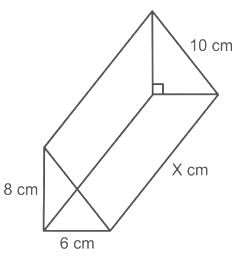
दिए गए प्रिज्म का परिमाप = 6 सेमी + 8 सेमी + 10 सेमी = 24 सेमी
दाएं त्रिकोणीय प्रिज्म का क्षेत्रफल = परिमाप x ऊँचाई
⇒ 24 x X = 288
⇒ X = 12 सेमी
एक समभुज त्रिकोण जिसकी भुजा 8 सेमी है, की ऊँचाई क्या है?- a)4√3 सेमी
- b)2√3 सेमी
- c)8√3 सेमी
- d)3√3 सेमी
Correct answer is option 'A'. Can you explain this answer?
एक समभुज त्रिकोण जिसकी भुजा 8 सेमी है, की ऊँचाई क्या है?
a)
4√3 सेमी
b)
2√3 सेमी
c)
8√3 सेमी
d)
3√3 सेमी
|
|
Learnpro Institute answered |
एक समभुज त्रिकोण की ऊँचाई
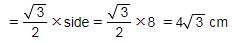
इसलिए, विकल्प A सही है।
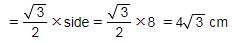
इसलिए, विकल्प A सही है।
एक त्रिकोणीय क्षेत्र को लोहे की तार से बाड़ा जाना है। बाड़ लगाने की लागत प्रति मीटर 15 रुपये है। यदि त्रिकोणीय क्षेत्र के तीन पक्षों में से दो के लंबाई का योग 25 मीटर है, तो निम्नलिखित में से कौन सी लागत क्षेत्र की बाड़ लगाने की नहीं हो सकती?- a)₹ 425
- b)675 रुपये
- c)₹ 725
- d)₹ 800
Correct answer is option 'D'. Can you explain this answer?
एक त्रिकोणीय क्षेत्र को लोहे की तार से बाड़ा जाना है। बाड़ लगाने की लागत प्रति मीटर 15 रुपये है। यदि त्रिकोणीय क्षेत्र के तीन पक्षों में से दो के लंबाई का योग 25 मीटर है, तो निम्नलिखित में से कौन सी लागत क्षेत्र की बाड़ लगाने की नहीं हो सकती?
a)
₹ 425
b)
675 रुपये
c)
₹ 725
d)
₹ 800

|
Iq Funda answered |
एक त्रिकोण के लिए, दो भुजाओं का योग हमेशा तीसरी भुजा से बड़ा होता है।
त्रिकोण की तीसरी भुजा को C मान लें।
यदि दो भुजाओं का योग 25 है,
तो 0 < c="">< 25="" c="" के="" लिए="" सत्य="">
C शून्य नहीं हो सकता और 25 से अधिक नहीं हो सकता।
त्रिकोण का परिमाण
= 25 < (त्रिकोण="" का="" परिमाण)=""><>
फेंसिंग की लागत प्रति मीटर 15 रुपये होगी, जो 375 - 750 के बीच होगी।
इसलिए, विकल्प D 800 रुपये फेंसिंग की लागत नहीं हो सकता।
त्रिकोण की तीसरी भुजा को C मान लें।
यदि दो भुजाओं का योग 25 है,
तो 0 < c="">< 25="" c="" के="" लिए="" सत्य="">
C शून्य नहीं हो सकता और 25 से अधिक नहीं हो सकता।
त्रिकोण का परिमाण
= 25 < (त्रिकोण="" का="" परिमाण)=""><>
फेंसिंग की लागत प्रति मीटर 15 रुपये होगी, जो 375 - 750 के बीच होगी।
इसलिए, विकल्प D 800 रुपये फेंसिंग की लागत नहीं हो सकता।
एक आयत के क्षेत्रफल का अनुपात एक वर्ग के क्षेत्रफल के साथ 3 : 5 है। यदि वर्ग का परिमाप 100 सेमी है, तो यदि आयत की चौड़ाई उसकी लंबाई से 66.67% अधिक है, तो आयत का परिमाप क्या हो सकता है?- a)75 सेमी
- b)80 सेमी
- c)85 सेमी
- d)65 सेमी
Correct answer is option 'B'. Can you explain this answer?
एक आयत के क्षेत्रफल का अनुपात एक वर्ग के क्षेत्रफल के साथ 3 : 5 है। यदि वर्ग का परिमाप 100 सेमी है, तो यदि आयत की चौड़ाई उसकी लंबाई से 66.67% अधिक है, तो आयत का परिमाप क्या हो सकता है?
a)
75 सेमी
b)
80 सेमी
c)
85 सेमी
d)
65 सेमी

|
Aim It Academy answered |
वर्ग की भुजा = 1000/4 = 25 सेमी
वर्ग का क्षेत्रफल = 25 × 25 = 625 वर्ग सेमी
आयत का क्षेत्रफल = 3x625 / 5 = 375 वर्ग सेमी
मान लें कि आयत की लंबाई = 3x और आयत की चौड़ाई = 3x का 166.67% = 5x, तो परिमाप =
2(l + b)
और क्षेत्रफल = 375 = 3x x 5x
x = 5 सेमी
परिमाप = 2(3x + 5x) = 16x = 80 सेमी
इसलिए, विकल्प B सही है।
आयत का क्षेत्रफल = 3x625 / 5 = 375 वर्ग सेमी
मान लें कि आयत की लंबाई = 3x और आयत की चौड़ाई = 3x का 166.67% = 5x, तो परिमाप =
2(l + b)
और क्षेत्रफल = 375 = 3x x 5x
x = 5 सेमी
परिमाप = 2(3x + 5x) = 16x = 80 सेमी
इसलिए, विकल्प B सही है।
यदि एक हॉल की लंबाई, चौड़ाई और ऊँचाई क्रमशः 20 मीटर, 10 मीटर और 20 मीटर हैं, तो हॉल का विकर्ण क्या होगा?- a)25 मीटर
- b)30 मीटर
- c)40 मीटर
- d)50 मीटर
Correct answer is option 'B'. Can you explain this answer?
यदि एक हॉल की लंबाई, चौड़ाई और ऊँचाई क्रमशः 20 मीटर, 10 मीटर और 20 मीटर हैं, तो हॉल का विकर्ण क्या होगा?
a)
25 मीटर
b)
30 मीटर
c)
40 मीटर
d)
50 मीटर

|
T.S Academy answered |
किसी कमरे का विकर्ण = √(l2 + b2 + h2)
इसलिए उत्तर = √(202 + 102 + 202) = √900 = 30 मीटर
इसलिए, विकल्प B सही है।
इसलिए उत्तर = √(202 + 102 + 202) = √900 = 30 मीटर
इसलिए, विकल्प B सही है।
यदि एक गोले का सतह क्षेत्र 1386 सेमी2 है, तो गोले का त्रिज्या ज्ञात करें।- a)12.5 सेंटीमीटर
- b)10.5 सेमी
- c)10 सेमी
- d)12 सेमी
Correct answer is option 'B'. Can you explain this answer?
यदि एक गोले का सतह क्षेत्र 1386 सेमी2 है, तो गोले का त्रिज्या ज्ञात करें।
a)
12.5 सेंटीमीटर
b)
10.5 सेमी
c)
10 सेमी
d)
12 सेमी

|
Spectrum Coaching Institute answered |
दिया गया:
एक गोले का सतही क्षेत्रफल = 1386 सेमी2
उपयोग किया गया सूत्र:
एक गोले का सतही क्षेत्रफल = 4πr2 जहाँ r गोले का त्रिज्या है।
गणना:
एक गोले का सतही क्षेत्रफल = 4πr2 = 1386

इसलिए, गोले की त्रिज्या 10.5 सेमी है।
1232 cm3 आयतन और 14 cm त्रिज्या वाले सिलिंडर की ऊँचाई क्या है?- a)2 सेंटीमीटर
- b)4 सेमी
- c)5 सेमी
- d)6 सेमी
Correct answer is option 'A'. Can you explain this answer?
1232 cm3 आयतन और 14 cm त्रिज्या वाले सिलिंडर की ऊँचाई क्या है?
a)
2 सेंटीमीटर
b)
4 सेमी
c)
5 सेमी
d)
6 सेमी

|
T.S Academy answered |
सिलेंडर का आयतन = πr2h = 1232
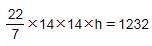
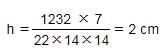
इसलिए, विकल्प A सही है।
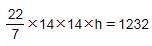
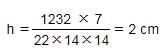
इसलिए, विकल्प A सही है।
यदि एक समबाहु त्रिकोण का क्षेत्रफल x है और उसकी परिधि y है, तो निम्नलिखित में से कौन सा सही है?- a)y4 = 432 x2
- b)y4 = 216 x2
- c)y2 = 432 x2
- d)इनमें से कोई नहीं
Correct answer is option 'A'. Can you explain this answer?
यदि एक समबाहु त्रिकोण का क्षेत्रफल x है और उसकी परिधि y है, तो निम्नलिखित में से कौन सा सही है?
a)
y4 = 432 x2
b)
y4 = 216 x2
c)
y2 = 432 x2
d)
इनमें से कोई नहीं

|
Spectrum Coaching Institute answered |
समबाहु त्रिकोण का क्षेत्रफल = √3a2/4 = x ......(i)
और परिधि = 3a = y
⇒ a = y/3 ....(ii)
अब, समीकरण (ii) से a का मान समीकरण (i) में डालने पर हमें मिलता है
√3 (y/3)2/4 = x
⇒ x = √3 x y2/36
⇒ x = y2/3√3x = y2/12√3
12√3 x = y2
दोनों पक्षों का वर्ग करने पर हमें मिलता है
y4 = 432x2
और परिधि = 3a = y
⇒ a = y/3 ....(ii)
अब, समीकरण (ii) से a का मान समीकरण (i) में डालने पर हमें मिलता है
√3 (y/3)2/4 = x
⇒ x = √3 x y2/36
⇒ x = y2/3√3x = y2/12√3
12√3 x = y2
दोनों पक्षों का वर्ग करने पर हमें मिलता है
y4 = 432x2
एक आयत की विकर्ण क्या है, जिसकी लंबाई 8 सेमी और चौड़ाई 6 सेमी है?- a)8 सेमी
- b)9 सेमी
- c)10 सेमी
- d)12 सेमी
Correct answer is option 'C'. Can you explain this answer?
एक आयत की विकर्ण क्या है, जिसकी लंबाई 8 सेमी और चौड़ाई 6 सेमी है?
a)
8 सेमी
b)
9 सेमी
c)
10 सेमी
d)
12 सेमी
|
|
Learnpro Institute answered |
आयत का विकर्ण = √(82 + 62) = √(64 + 36) = √100 = 10 सेमी
इसलिए, विकल्प C सही है।
इसलिए, विकल्प C सही है।
एक पिरामिड की कुल सतह क्षेत्रफल जिसका आधार एक नियमित बहुभुज है 260 cm2 है और इसके आधार का क्षेत्रफल 120 cm2 है। प्रत्येक पार्श्व चेहरे का क्षेत्रफल 20 cm2 है। तब पार्श्व चेहरों की संख्या क्या होगी?- a)7
- b)8
- c)6
- d)5
Correct answer is option 'A'. Can you explain this answer?
एक पिरामिड की कुल सतह क्षेत्रफल जिसका आधार एक नियमित बहुभुज है 260 cm2 है और इसके आधार का क्षेत्रफल 120 cm2 है। प्रत्येक पार्श्व चेहरे का क्षेत्रफल 20 cm2 है। तब पार्श्व चेहरों की संख्या क्या होगी?
a)
7
b)
8
c)
6
d)
5

|
Glance Learning Institute answered |
कुल सतह क्षेत्रफल = पार्श्व सतह क्षेत्रफल + आधार का क्षेत्रफल
260 = पार्श्व सतह क्षेत्रफल + 120
पार्श्व सतह क्षेत्रफल = 260 – 120 = 140 cm2
प्रत्येक पार्श्व चेहरे का क्षेत्रफल = 20 cm2
पार्श्व चेहरों की संख्या = 140/20 = 7
260 = पार्श्व सतह क्षेत्रफल + 120
पार्श्व सतह क्षेत्रफल = 260 – 120 = 140 cm2
प्रत्येक पार्श्व चेहरे का क्षेत्रफल = 20 cm2
पार्श्व चेहरों की संख्या = 140/20 = 7
क्यूब की भुजा की लंबाई 5.6 सेमी है। उस क्यूब से निकाली जा सकने वाली सबसे बड़ी गेंद का आयतन क्या है?- a)91.98 सेमी3
- b)99.96 सेमी3
- c)96.98 सेमी3
- d)90.69 सेमी3
Correct answer is option 'A'. Can you explain this answer?
क्यूब की भुजा की लंबाई 5.6 सेमी है। उस क्यूब से निकाली जा सकने वाली सबसे बड़ी गेंद का आयतन क्या है?
a)
91.98 सेमी3
b)
99.96 सेमी3
c)
96.98 सेमी3
d)
90.69 सेमी3

|
Wizius Careers answered |
दिया गया:
क्यूब की भुजा = 5.6 सेमी
उपयोग किया गया सूत्र:
गेंद का आयतन = (4/3) × π × r3
गणना:
गेंद का व्यास = क्यूब की भुजा
⇒ 2 × गेंद का त्रिज्या = 5.6 सेमी
⇒ गेंद का त्रिज्या = 5.6/2 = 2.8 सेमी
गेंद का आयतन = (4/3) × (22/7) × (2.8)3
⇒ 88/21 × 21.952
⇒ 91.98
∴ उस क्यूब से निकाली जा सकने वाली सबसे बड़ी गेंद का आयतन 91.98 सेमी3 है।
⇒ 2 × गेंद का त्रिज्या = 5.6 सेमी
⇒ गेंद का त्रिज्या = 5.6/2 = 2.8 सेमी
गेंद का आयतन = (4/3) × (22/7) × (2.8)3
⇒ 88/21 × 21.952
⇒ 91.98
∴ उस क्यूब से निकाली जा सकने वाली सबसे बड़ी गेंद का आयतन 91.98 सेमी3 है।
एक ठोस शंकु जिसका व्यास 7 सेमी और ऊँचाई 7 सेमी है, को दो ठोस गोलों (स्फियर) के साथ पिघलाया गया, जिनका व्यास भी 7 सेमी है, ताकि एक ठोस बेलन (सिलिंडर) का निर्माण हो सके जिसका व्यास 7 सेमी है। बेलन का वक्र सतह क्षेत्रफल (सेमी2 में) क्या है? (π = 22/7 का उपयोग करें)- a)880
- b)482
- c)924
- d)उपरोक्त में से कोई नहीं
Correct answer is option 'C'. Can you explain this answer?
एक ठोस शंकु जिसका व्यास 7 सेमी और ऊँचाई 7 सेमी है, को दो ठोस गोलों (स्फियर) के साथ पिघलाया गया, जिनका व्यास भी 7 सेमी है, ताकि एक ठोस बेलन (सिलिंडर) का निर्माण हो सके जिसका व्यास 7 सेमी है। बेलन का वक्र सतह क्षेत्रफल (सेमी2 में) क्या है? (π = 22/7 का उपयोग करें)
a)
880
b)
482
c)
924
d)
उपरोक्त में से कोई नहीं

|
T.S Academy answered |
प्रस्तुत:
एक ठोस शंकु जिसका त्रिज्या 7 सेमी और ऊँचाई 7 सेमी थी, को दो ठोस गोले के साथ पिघलाया गया, जिनकी त्रिज्या भी 7 सेमी है, ताकि एक ठोस बेलन का निर्माण हो सके जिसकी त्रिज्या 7 सेमी है।
उपयोग में लाया गया सूत्र:
शंकु का आयतन = 1/3πr2h
बेलन का आयतन = πr2h
गोले का आयतन = 4/3πr3
बेलन का वक्र सतही क्षेत्र = 2πrh
यहाँ,
r = त्रिज्या
h = ऊँचाई
बेलन का आयतन = πr2h
गोले का आयतन = 4/3πr3
बेलन का वक्र सतही क्षेत्र = 2πrh
यहाँ,
r = त्रिज्या
h = ऊँचाई
गणना:
शंकु का आयतन = 1/3π × 72 × 7
⇒ 1/3π x 49
⇒ 1/3π x 49
प्रत्येक गोले का आयतन = 4/3π × 73
मान लेते हैं कि बने हुए बेलन की ऊँचाई H है
प्रश्न के अनुसार,
मान लेते हैं कि बने हुए बेलन की ऊँचाई H है
प्रश्न के अनुसार,

इसलिए, बने हुए बेलन की ऊँचाई 21 सेमी है
अब,
बेलन का वक्र सतही क्षेत्र = 2 x 22/7 x 7 x 21
⇒ 924
∴ बेलन का वक्र सतही क्षेत्र (सेमी2) 924 है।
अब,
बेलन का वक्र सतही क्षेत्र = 2 x 22/7 x 7 x 21
⇒ 924
∴ बेलन का वक्र सतही क्षेत्र (सेमी2) 924 है।
शंकु के आधार की परिधि 132 सेमी है। शंकु की तिरछी ऊँचाई और आधार के त्रिज्या के बीच का अंतर 8 सेमी है। शंकु का आयतन ज्ञात करें।- a)1914 सेमी3
- b)8950 सेमी3
- c)9240 सेमी3
- d)उपरोक्त में से एक से अधिक
Correct answer is option 'C'. Can you explain this answer?
शंकु के आधार की परिधि 132 सेमी है। शंकु की तिरछी ऊँचाई और आधार के त्रिज्या के बीच का अंतर 8 सेमी है। शंकु का आयतन ज्ञात करें।
a)
1914 सेमी3
b)
8950 सेमी3
c)
9240 सेमी3
d)
उपरोक्त में से एक से अधिक

|
Aim It Academy answered |
दिया गया,
कोन के आधार का परिमाण = 132
कोन का त्रिज्या = 132 × 7/22 × 1/2 = 21 सेमी
तब,
कोन की झुकी हुई ऊँचाई = 21 + 8 = 29 सेमी
पाइथागोरस के प्रमेय का उपयोग करते हुए,
⇒ (झुकी हुई ऊँचाई)2 = (ऊँचाई)2 + (त्रिज्या)2
⇒ ऊँचाई2 = 292 – 212
⇒ ऊँचाई = 20 सेमी
कोन का आयतन = 1/3 × πr2h
= 1/3 × 22/7 × 21 × 21 × 20
= 9240 सेमी3
कोन का त्रिज्या = 132 × 7/22 × 1/2 = 21 सेमी
तब,
कोन की झुकी हुई ऊँचाई = 21 + 8 = 29 सेमी
पाइथागोरस के प्रमेय का उपयोग करते हुए,
⇒ (झुकी हुई ऊँचाई)2 = (ऊँचाई)2 + (त्रिज्या)2
⇒ ऊँचाई2 = 292 – 212
⇒ ऊँचाई = 20 सेमी
कोन का आयतन = 1/3 × πr2h
= 1/3 × 22/7 × 21 × 21 × 20
= 9240 सेमी3
एक फ्रustum की ऊपरी त्रिज्या 20 सेमी और निचला व्यास 60 सेमी है। इस फ्रustum की ऊँचाई 40 सेमी है। अब, इस फ्रustum पर एक दाहिनी गोल शंकु भरा जाना है ताकि निर्मित संरचना एक दाहिनी गोल शंकु हो। उस शंकु की ऊँचाई क्या होनी चाहिए जो भरी जानी है?- a)60 सेमी
- b)80 सेमी
- c)40 सेमी
- d)100 सेमी
Correct answer is option 'B'. Can you explain this answer?
एक फ्रustum की ऊपरी त्रिज्या 20 सेमी और निचला व्यास 60 सेमी है। इस फ्रustum की ऊँचाई 40 सेमी है। अब, इस फ्रustum पर एक दाहिनी गोल शंकु भरा जाना है ताकि निर्मित संरचना एक दाहिनी गोल शंकु हो। उस शंकु की ऊँचाई क्या होनी चाहिए जो भरी जानी है?
a)
60 सेमी
b)
80 सेमी
c)
40 सेमी
d)
100 सेमी

|
Learning Education answered |
दिया गया:
फ्रustum की ऊपरी त्रिज्या (r1) = 20 सेमी
फ्रustum की निचली त्रिज्या (r2) = 60/2 = 30 सेमी (क्योंकि व्यास दिया गया है)
फ्रustum की ऊँचाई (h1) = 40 सेमी
फ्रustum की निचली त्रिज्या (r2) = 60/2 = 30 सेमी (क्योंकि व्यास दिया गया है)
फ्रustum की ऊँचाई (h1) = 40 सेमी
गणना:
ऊँचाई और त्रिज्या का अनुपात



∴ भरी जाने वाली शंकु की ऊँचाई 80 सेमी होनी चाहिए।
एक सही प्रिस्म का आधार एक नियमित षट्भुज है, जिसका पक्ष 5 सेमी है। यदि इसकी ऊँचाई 12√3 सेमी है, तो इसका आयतन (सेमी3) क्या होगा:- a)1800
- b)900
- c)1350
- d)670
Correct answer is option 'C'. Can you explain this answer?
एक सही प्रिस्म का आधार एक नियमित षट्भुज है, जिसका पक्ष 5 सेमी है। यदि इसकी ऊँचाई 12√3 सेमी है, तो इसका आयतन (सेमी3) क्या होगा:
a)
1800
b)
900
c)
1350
d)
670

|
Wizius Careers answered |
दी गई जानकारी :-
एक सही प्रिस्म का आधार एक नियमित षट्भुज है, जिसका पक्ष 5 सेमी है।
ऊँचाई 12√3 सेमी है।
सिद्धांत :-
प्रिस्म एक सिलेंडर का एक भाग है, इसलिए,
प्रिस्म का आयतन = आधार × ऊँचाई
चूंकि प्रिस्म का आधार षट्भुज है, इसलिए
आधार क्षेत्र = आधार क्षेत्र x ऊँचाई
आधार क्षेत्र = षट्भुज का क्षेत्र = 6 समभुज त्रिकोणों का क्षेत्र = 6 x (√3/4) x पक्ष2
गणना :-
गणना :-
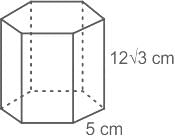
⇒ आधार क्षेत्र = 6 x (√3/4) x 52
⇒ आधार क्षेत्र = 150 x (√3/4)
⇒ आयतन = 150 x (√3/4) x 12√3
⇒ आयतन = (1800 x 3)/4
⇒ आयतन = 1350 सेमी3
∴ आयतन = 1350 सेमी3
त्रिभुज ABC में, BC = 5 सेमी, AC = 12 सेमी और AB = 13 सेमी है। AC पर B से खींची गई ऊँचाई की लंबाई क्या है?- a)4 सेमी
- b)5 सेमी
- c)6 सेमी
- d)7 सेमी
Correct answer is option 'B'. Can you explain this answer?
त्रिभुज ABC में, BC = 5 सेमी, AC = 12 सेमी और AB = 13 सेमी है। AC पर B से खींची गई ऊँचाई की लंबाई क्या है?
a)
4 सेमी
b)
5 सेमी
c)
6 सेमी
d)
7 सेमी

|
Spectrum Coaching Institute answered |
∵ s= (13 + 5 + 12) / 2 सेमी
= 15 सेमी
s-a = 2 सेमी,
s-b = 10 सेमी और
s-c = 3 सेमी
⇒ क्षेत्रफल = √ (15 x 2 x 10 x 3 ) सेमी2
= 30 सेमी2
⇒ (12 x h) / 2 = 30
∴ h = 5 सेमी
= 15 सेमी
s-a = 2 सेमी,
s-b = 10 सेमी और
s-c = 3 सेमी
⇒ क्षेत्रफल = √ (15 x 2 x 10 x 3 ) सेमी2
= 30 सेमी2
⇒ (12 x h) / 2 = 30
∴ h = 5 सेमी
एक आयताकार भूखंड की लंबाई उसकी चौड़ाई से आधी लंबी है। लॉन का क्षेत्रफल 2/3 हेक्टेयर है। भूखंड की लंबाई क्या है?- a)100 मीटर
- b)66.66 मीटर
- c)33 मीटर
- d)(100/ √ 3 ) मीटर
Correct answer is option 'A'. Can you explain this answer?
एक आयताकार भूखंड की लंबाई उसकी चौड़ाई से आधी लंबी है। लॉन का क्षेत्रफल 2/3 हेक्टेयर है। भूखंड की लंबाई क्या है?
a)
100 मीटर
b)
66.66 मीटर
c)
33 मीटर
d)
(100/ √ 3 ) मीटर

|
Wizius Careers answered |
मान लें चौड़ाई = b मीटर।
फिर, लंबाई = 3b/2 मीटर
∴ b x 3b/2 = 2/3 X 10000
⇒ b2 = (4 x 10000)/9
⇒ b = ( 2 X 100)/3 मीटर
∴ लंबाई = (3/2) x (2/3) x 100 मीटर
= 100 मीटर
फिर, लंबाई = 3b/2 मीटर
∴ b x 3b/2 = 2/3 X 10000
⇒ b2 = (4 x 10000)/9
⇒ b = ( 2 X 100)/3 मीटर
∴ लंबाई = (3/2) x (2/3) x 100 मीटर
= 100 मीटर
जिस वृत्त का त्रिज्या 3 सेंटीमीटर है, उसका व्यास क्या है?- a)6 सेंटीमीटर
- b)12 सेंटीमीटर
- c)1.5 सेंटीमीटर
- d)8 सेंटीमीटर
Correct answer is option 'A'. Can you explain this answer?
जिस वृत्त का त्रिज्या 3 सेंटीमीटर है, उसका व्यास क्या है?
a)
6 सेंटीमीटर
b)
12 सेंटीमीटर
c)
1.5 सेंटीमीटर
d)
8 सेंटीमीटर
|
|
Learnpro Institute answered |
त्रिज्या = व्यास/2
∴ व्यास = 2 x त्रिज्या
= 2 x 3
= 6 सेंटीमीटर
∴ व्यास = 2 x त्रिज्या
= 2 x 3
= 6 सेंटीमीटर
एक तांबे का गोला जिसका व्यास 18 सेमी है, उसे 6 मिमी व्यास के तार में ढाला गया है। तार की लंबाई ज्ञात कीजिए।- a)143 मीटर
- b)108 मीटर
- c)324 मीटर
- d)234 मीटर
Correct answer is option 'B'. Can you explain this answer?
एक तांबे का गोला जिसका व्यास 18 सेमी है, उसे 6 मिमी व्यास के तार में ढाला गया है। तार की लंबाई ज्ञात कीजिए।
a)
143 मीटर
b)
108 मीटर
c)
324 मीटर
d)
234 मीटर

|
Spectrum Coaching Institute answered |
दी गई जानकारी:
एक तांबे का गोला जिसका व्यास 18 सेमी है, उसे 6 मिमी व्यास के तार में ढाला गया है।
उपयोग की गई अवधारणा:
गोले का आयतन = 4/3πr3
सिलेंडर का आयतन = πr2h
सिलेंडर का आयतन = πr2h
गणना:
गोले का त्रिज्या = 9 सेमी
तार का त्रिज्या = 0.3 सेमी [क्योंकि 1 सेमी = 10 मिमी]
प्रश्न के अनुसार,
गोले का आयतन = सिलेंडर का आयतन
गोले का त्रिज्या = 9 सेमी
तार का त्रिज्या = 0.3 सेमी [क्योंकि 1 सेमी = 10 मिमी]
प्रश्न के अनुसार,
गोले का आयतन = सिलेंडर का आयतन
∴ तार की लंबाई 108 मीटर है।

यदि तीन ठोस सोने की गोलाकार मोतियाँ जिनकी त्रिज्याएँ क्रमशः 6 सेमी, 8 सेमी, और 10 सेमी हैं, को एक गोलाकार मोती में पिघलाया जाता है, तो बड़े मोती की त्रिज्या (सेमी में) क्या होगी?- a)16 सेमी
- b)15 सेमी
- c)13 सेमी
- d)उपरोक्त में से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
यदि तीन ठोस सोने की गोलाकार मोतियाँ जिनकी त्रिज्याएँ क्रमशः 6 सेमी, 8 सेमी, और 10 सेमी हैं, को एक गोलाकार मोती में पिघलाया जाता है, तो बड़े मोती की त्रिज्या (सेमी में) क्या होगी?
a)
16 सेमी
b)
15 सेमी
c)
13 सेमी
d)
उपरोक्त में से कोई नहीं

|
Learning Education answered |
दिया गया:
त्रिज्या r1 = 6 सेमी, r2 = 8 सेमी, r3 = 10 सेमी के गोलों को एक में पिघलाया गया।
उपयोग किया गया सूत्र:
गोल का आयतन = 4/3π r3
गणना:
चलो बड़े मोती की त्रिज्या को 'R' मान लेते हैं।
प्रश्न के अनुसार,
छोटे मोतियों का आयतन = बड़े मोती का आयतन
⇒ 4/3π [(6)3 + (8)3 + (10)3] = 4/3π R3
⇒ R3 = [(216) + (512) + (1000)]
⇒ R3 = 1728 = 12 सेमी।
∴ बड़े मोती की त्रिज्या (सेमी में) 12 सेमी होगी।
प्रश्न के अनुसार,
छोटे मोतियों का आयतन = बड़े मोती का आयतन
⇒ 4/3π [(6)3 + (8)3 + (10)3] = 4/3π R3
⇒ R3 = [(216) + (512) + (1000)]
⇒ R3 = 1728 = 12 सेमी।
∴ बड़े मोती की त्रिज्या (सेमी में) 12 सेमी होगी।
एक रबर की गेंद के क्रॉस-सेक्शन का बाहरी व्यास 22 इंच है। रबर की मोटाई 0.5 इंच है। निकटतम वर्ग इंच में, गेंद की आंतरिक सतह का क्षेत्रफल क्या होगा? (π का मान 3.14 मानें)।- a)253 वर्ग इंच
- b)3124.62 वर्ग इंच
- c)1384.74 वर्ग इंच
- d)2314.82 वर्ग इंच
Correct answer is option 'C'. Can you explain this answer?
एक रबर की गेंद के क्रॉस-सेक्शन का बाहरी व्यास 22 इंच है। रबर की मोटाई 0.5 इंच है। निकटतम वर्ग इंच में, गेंद की आंतरिक सतह का क्षेत्रफल क्या होगा? (π का मान 3.14 मानें)।
a)
253 वर्ग इंच
b)
3124.62 वर्ग इंच
c)
1384.74 वर्ग इंच
d)
2314.82 वर्ग इंच
|
|
Learnpro Institute answered |
दी गई जानकारी:
रबर के गेंद का बाहरी व्यास = 22 इंच।
मोटाई = 0.5 इंच
उपयोग किया गया सूत्र:
गेंद का सतही क्षेत्र = 4πr2 [जहाँ, r गेंद का त्रिज्या है]
गेंद का आंतरिक त्रिज्या = बाहरी त्रिज्या - मोटाई
व्यास = 2 × त्रिज्या
गणनाएँ:
बाहरी व्यास = 22

रबर के गेंद का आंतरिक त्रिज्या = 11 - 0.5 = 10.5 इंच
अब, रबर के गेंद के आंतरिक सतह का क्षेत्रफल = 4 x 3.14 x 10.52
= 4 × 3.14 × 110.25
= 1384.74 वर्ग इंच
∴ उत्तर है 1384.74 वर्ग इंच।
यदि एक आयत के भुजाओं को 5% बढ़ाया जाता है, तो इसके विकर्णों में प्रतिशत वृद्धि क्या होगी?- a)6%
- b)4%
- c)5%
- d)9%
Correct answer is option 'C'. Can you explain this answer?
यदि एक आयत के भुजाओं को 5% बढ़ाया जाता है, तो इसके विकर्णों में प्रतिशत वृद्धि क्या होगी?
a)
6%
b)
4%
c)
5%
d)
9%

|
Wizius Careers answered |
सूत्र के अनुसार,
विकर्णों में प्रतिशत वृद्धि = 5%
विकर्णों में प्रतिशत वृद्धि = 5%
एक बेलन और एक शंकु के आयतन का योग 2190π सेमी2 है। दोनों बेलन और शंकु की त्रिज्या समान है, अर्थात्, 10 सेमी। यदि शंकु की ऊँचाई 15 सेमी है, तो बेलन की ऊँचाई की शंकु की ऊँचाई के साथ अनुपात ज्ञात कीजिए?- a)173/152
- b)169/150
- c)156/149
- d)191/136
Correct answer is option 'B'. Can you explain this answer?
एक बेलन और एक शंकु के आयतन का योग 2190π सेमी2 है। दोनों बेलन और शंकु की त्रिज्या समान है, अर्थात्, 10 सेमी। यदि शंकु की ऊँचाई 15 सेमी है, तो बेलन की ऊँचाई की शंकु की ऊँचाई के साथ अनुपात ज्ञात कीजिए?
a)
173/152
b)
169/150
c)
156/149
d)
191/136

|
Learning Education answered |
मान लीजिए कि बेलन की ऊँचाई = h'
बेलन का आयतन = πr2h
बेलन का आयतन = πr2h



इसलिए, विकल्प B सही है।
पी और क्यू दो समवृत्त वृत्तों की परिधि पर दौड़ रहे हैं, जिसमें बड़े वृत्त की त्रिज्या आंतरिक वृत्त की परिधि का आधा है। पी बड़े वृत्त पर और क्यू छोटे वृत्त पर दौड़ता है और दोनों एक ही समय में एक चक्कर पूरा करते हैं। यदि दोनों बड़े वृत्त पर दौड़ते हैं, तो पी क्यू को एक ही दिशा में दौड़ते समय 75 मीटर से हरा देगा, तो बड़े वृत्त की परिधि क्या है?- a)145 मीटर
- b)165 मीटर
- c)110 मीटर
- d)225 मीटर
Correct answer is option 'C'. Can you explain this answer?
पी और क्यू दो समवृत्त वृत्तों की परिधि पर दौड़ रहे हैं, जिसमें बड़े वृत्त की त्रिज्या आंतरिक वृत्त की परिधि का आधा है। पी बड़े वृत्त पर और क्यू छोटे वृत्त पर दौड़ता है और दोनों एक ही समय में एक चक्कर पूरा करते हैं। यदि दोनों बड़े वृत्त पर दौड़ते हैं, तो पी क्यू को एक ही दिशा में दौड़ते समय 75 मीटर से हरा देगा, तो बड़े वृत्त की परिधि क्या है?
a)
145 मीटर
b)
165 मीटर
c)
110 मीटर
d)
225 मीटर

|
Target Study Academy answered |
आइए आंतरिक वृत्त का त्रिज्या = R मान लें।
आंतरिक वृत्त का परिधि = 2πR
बड़े वृत्त का त्रिज्या = πR
बड़े वृत्त का परिधि = 2π (πR)
चूंकि दोनों एक ही समय में 1 चक्कर पूरा करते हैं, उनके गति का अनुपात उनके द्वारा तय की गई दूरी के अनुपात के बराबर होगा।
आंतरिक वृत्त का परिधि = 2πR
बड़े वृत्त का त्रिज्या = πR
बड़े वृत्त का परिधि = 2π (πR)
चूंकि दोनों एक ही समय में 1 चक्कर पूरा करते हैं, उनके गति का अनुपात उनके द्वारा तय की गई दूरी के अनुपात के बराबर होगा।

जब दोनों बड़े ट्रैक पर दौड़ते हैं तो उनके द्वारा तय की गई दूरी का अंतर (22 – 7) =
15 इकाई होगी।
15 इकाई = 75 मीटर
1 इकाई = 5 मीटर
P एक चक्कर पूरा करता है। तो 1 चक्कर = 22 इकाई
कुल दूरी = 22 × 5 = 110 मीटर
इसलिए, विकल्प C सही है।
15 इकाई होगी।
15 इकाई = 75 मीटर
1 इकाई = 5 मीटर
P एक चक्कर पूरा करता है। तो 1 चक्कर = 22 इकाई
कुल दूरी = 22 × 5 = 110 मीटर
इसलिए, विकल्प C सही है।
यदि एक वृत्त का क्षेत्रफल 346.50 सेमी2 है, तो उस वृत्त की परिधि क्या होगी?- a)50 सेमी
- b)56 सेंटीमीटर
- c)62 सेमी
- d)66 सेमी
Correct answer is option 'D'. Can you explain this answer?
यदि एक वृत्त का क्षेत्रफल 346.50 सेमी2 है, तो उस वृत्त की परिधि क्या होगी?
a)
50 सेमी
b)
56 सेंटीमीटर
c)
62 सेमी
d)
66 सेमी

|
Learning Education answered |
πr2 = 346.50
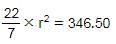
r2 = 110.25
r = 10.50
इसलिए उत्तर = 2πr
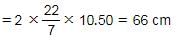
इसलिए, विकल्प D सही है।
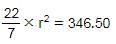
r2 = 110.25
r = 10.50
इसलिए उत्तर = 2πr
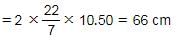
इसलिए, विकल्प D सही है।
Chapter doubts & questions for मापन: आयतन, सतही क्षेत्र और ठोस आकृतियाँ - CSAT की तैयारी (हिंदी) 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of मापन: आयतन, सतही क्षेत्र और ठोस आकृतियाँ - CSAT की तैयारी (हिंदी) in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily