All Exams >
Class 10 >
Mathematics Class 10 ICSE >
All Questions
All questions of Mensuration: Cylinder, Cone and Sphere for Class 10 Exam
A pole has to be erected on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. The distance of the pole from one of the gates is:(2011)- a)8 metres
- b)8.25 metres
- c)5 metres
- d)None these
Correct answer is option 'C'. Can you explain this answer?
A pole has to be erected on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. The distance of the pole from one of the gates is:
(2011)
a)
8 metres
b)
8.25 metres
c)
5 metres
d)
None these
|
Krishna Iyer answered |
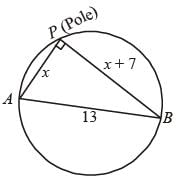
In right ΔAPB,
x2 + (x + 7)2 = 132
⇒ x = 5 ∴ x + 7 = 12.
A rectangle with perimeter 88 m is partitioned into 5 congruent rectangles, as shown in the diagram given below. The perimeter of each of the congruent rectangles is
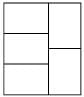(2012)- a)20 m
- b)32 m
- c)48 m
- d)40 m
Correct answer is option 'D'. Can you explain this answer?
A rectangle with perimeter 88 m is partitioned into 5 congruent rectangles, as shown in the diagram given below. The perimeter of each of the congruent rectangles is
(2012)
a)
20 m
b)
32 m
c)
48 m
d)
40 m
|
Vikas Kapoor answered |
Let the lengths and breaths of each,
Small rectangles be 'x' meter and 'y' meter respectively.
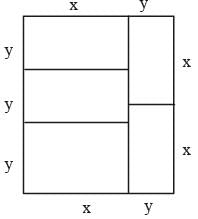
∵ Perimeter = 88 m
∴ 5y + 4x = 88 and 3y = 2x
∴ 5y + 3y × 2 = 88
5y + 6y = 88 ⇒ 11y = 88
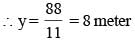
∴ 5 × 8 + 4x = 88
4x = 88 – 40 = 48
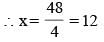
∴ Perimeter of each small rectangle = 2 (x + y)
= 2 (12 + 8) = 40 meter.
Small rectangles be 'x' meter and 'y' meter respectively.
∵ Perimeter = 88 m
∴ 5y + 4x = 88 and 3y = 2x
∴ 5y + 3y × 2 = 88
5y + 6y = 88 ⇒ 11y = 88
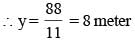
∴ 5 × 8 + 4x = 88
4x = 88 – 40 = 48
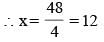
∴ Perimeter of each small rectangle = 2 (x + y)
= 2 (12 + 8) = 40 meter.
ABCD is an isosceles trapezium with BC = AD = 10 units, AB = 2 units and CD = 14 units. The mid-points of the sides of the trapezium are joined to form a quadrilateral PQRS. Find the ratio of the area of the circle inscribed in the quadrilateral PQRS to the area of trapezium ABCD.(2015)- a)
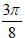
- b)
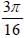
- c)
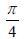
- d)
Correct answer is option 'D'. Can you explain this answer?
ABCD is an isosceles trapezium with BC = AD = 10 units, AB = 2 units and CD = 14 units. The mid-points of the sides of the trapezium are joined to form a quadrilateral PQRS. Find the ratio of the area of the circle inscribed in the quadrilateral PQRS to the area of trapezium ABCD.
(2015)
a)
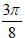
b)
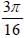
c)
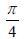
d)
|
Lavanya Menon answered |
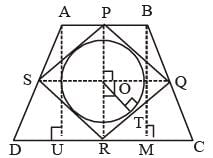
PQRS is a rhombus, so the centre of the inscribed circle will be the center of the rhombus PQRS
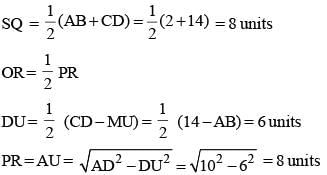
PR = SQ = 8 units
⇒ PQRS is a square
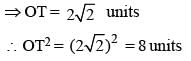
Area of trapezium =
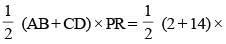8 = 64 sq. unit.Required ratio =
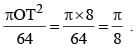
The smallest possible circle touching two opposite sides of a rectangle is cut-out from a rectangle of area 60 sq. units. If the area of this circle is 3/2 times the area left out in the rectangle, find the length of the smaller side of the rectangle.(2015)- a)
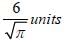
- b)
- c)
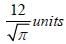
- d)
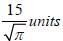
Correct answer is option 'C'. Can you explain this answer?
The smallest possible circle touching two opposite sides of a rectangle is cut-out from a rectangle of area 60 sq. units. If the area of this circle is 3/2 times the area left out in the rectangle, find the length of the smaller side of the rectangle.
(2015)
a)
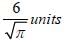
b)
c)
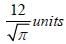
d)
|
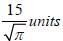
BT Educators answered |
Let length of smaller side of rectangle = a
∴ Radius = a/2 of circle
According to question,
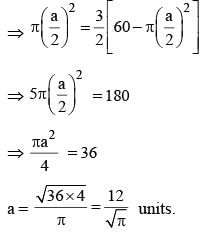
So, length of smaller side of rectangle =
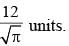
A regular polygon has an even number of sides. If the product of the length of its side and the distance between two opposite sides is 1/4 th of its area, find number of sides it has(2016)- a)6
- b)8
- c)20
- d)16
Correct answer is option 'D'. Can you explain this answer?
A regular polygon has an even number of sides. If the product of the length of its side and the distance between two opposite sides is 1/4 th of its area, find number of sides it has
(2016)
a)
6
b)
8
c)
20
d)
16
|
Arun Sharma answered |
Let the number of sides be 2n. Let the length of the side of S and the length of the perpendicular from the centre to each side be P. Since the number of sides is even, the opposite sides will be parallel and the distance between any two opposite sides is equal to 2P.
Also, area of the polygon (A) =
...(i)
According to question,
S(2P) = A/4 or SP = A/8
∴ (1) ⇒ A = n (A/8)
⇒ n = 8 or 2n = 16
∴ number of sides = 16.
Also, area of the polygon (A) =
...(i)According to question,
S(2P) = A/4 or SP = A/8
∴ (1) ⇒ A = n (A/8)
⇒ n = 8 or 2n = 16
∴ number of sides = 16.
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to(2017)- a)10
- b)50
- c)60
- d)20
Correct answer is option 'B'. Can you explain this answer?
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
(2017)
a)
10
b)
50
c)
60
d)
20
|
Meera Rana answered |
Volume ratio of 5 smaller and original cube = 1:1 : 8 : 27 : 27 : 64
Side ratio of 5 smaller and original cube = 1 : 1 : 2 : 3 : 3 : 4
Surface area ratio of 5 smaller and original cube = 1 : 1 : 4 : 9 : 9 : 16
Sum of smaller cube (surface area) = 24 parts.
Big cube = 16 parts.
The sum is 50% greater.
Side ratio of 5 smaller and original cube = 1 : 1 : 2 : 3 : 3 : 4
Surface area ratio of 5 smaller and original cube = 1 : 1 : 4 : 9 : 9 : 16
Sum of smaller cube (surface area) = 24 parts.
Big cube = 16 parts.
The sum is 50% greater.
How many triangles can be drawn by joining any three vertices of a pentagon?(2013)- a)8
- b)9
- c)11
- d)10
Correct answer is option 'D'. Can you explain this answer?
How many triangles can be drawn by joining any three vertices of a pentagon?
(2013)
a)
8
b)
9
c)
11
d)
10
|
Saanvi Pillai answered |
Number of Triangles in a Pentagon
There are a total of 5 vertices in a pentagon. To form a triangle, we need to select any 3 vertices out of these 5 vertices.
Calculating the Number of Triangles
- If we select 3 vertices that are not adjacent to each other, we can form 1 triangle.
- If we select 2 adjacent vertices and 1 non-adjacent vertex, we can form 2 triangles.
- If we select 2 non-adjacent vertices and 1 adjacent vertex, we can form 2 triangles.
- If we select 3 adjacent vertices, we can form 1 triangle.
Therefore, the total number of triangles that can be formed by joining any three vertices of a pentagon is 1 + 2 + 2 + 1 = 6.
Additional Triangles
However, we need to consider the triangles formed by the diagonals of the pentagon as well. Each diagonal forms a triangle with one side of the pentagon.
- There are 5 diagonals in a pentagon.
- Each diagonal forms 1 triangle with one side of the pentagon.
- Therefore, the number of additional triangles formed by the diagonals is 5.
Total Number of Triangles
Adding the triangles formed by selecting vertices and the triangles formed by the diagonals, we get a total of 6 + 5 = 11 triangles that can be drawn by joining any three vertices of a pentagon.
Therefore, the correct answer is option D) 11.
There are a total of 5 vertices in a pentagon. To form a triangle, we need to select any 3 vertices out of these 5 vertices.
Calculating the Number of Triangles
- If we select 3 vertices that are not adjacent to each other, we can form 1 triangle.
- If we select 2 adjacent vertices and 1 non-adjacent vertex, we can form 2 triangles.
- If we select 2 non-adjacent vertices and 1 adjacent vertex, we can form 2 triangles.
- If we select 3 adjacent vertices, we can form 1 triangle.
Therefore, the total number of triangles that can be formed by joining any three vertices of a pentagon is 1 + 2 + 2 + 1 = 6.
Additional Triangles
However, we need to consider the triangles formed by the diagonals of the pentagon as well. Each diagonal forms a triangle with one side of the pentagon.
- There are 5 diagonals in a pentagon.
- Each diagonal forms 1 triangle with one side of the pentagon.
- Therefore, the number of additional triangles formed by the diagonals is 5.
Total Number of Triangles
Adding the triangles formed by selecting vertices and the triangles formed by the diagonals, we get a total of 6 + 5 = 11 triangles that can be drawn by joining any three vertices of a pentagon.
Therefore, the correct answer is option D) 11.
The top and bottom radii of a frustrum of a solid cone are 3 cm and 6 cm respectively. Its height is 8 cm. There is a conical cavity of height 3 cm and radius 6 cm at the bottom. The amount of material in the solid is(2014)- a)132 π cm3
- b)168 π cm3
- c)159 π cm3
- d)Data Insufficient
Correct answer is option 'A'. Can you explain this answer?
The top and bottom radii of a frustrum of a solid cone are 3 cm and 6 cm respectively. Its height is 8 cm. There is a conical cavity of height 3 cm and radius 6 cm at the bottom. The amount of material in the solid is
(2014)
a)
132 π cm3
b)
168 π cm3
c)
159 π cm3
d)
Data Insufficient
|
|
Alok Verma answered |
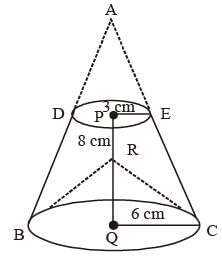
Here, ABC represents cone; DEBC represents frustum which was made by cone and BRC represents conical cavity.
So, Volume of material = cone ABC – (cone ADE + conical cavity of BRC).
Now, ΔAPE and ΔAQC are similary,
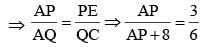
⇒ So, AP = 8 cm.
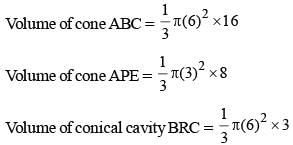
Required volume of solid =
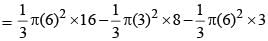
= 132π cm3.
A circle of radius 6.5 cm is circumscribed around a right-angled triangle with the sides a, b and c cm where a, b and c are natural numbers. What is the perimeter of the triangle?(2012)- a)30 cm
- b)26 cm
- c)28 cm
- d)32 cm
Correct answer is option 'A'. Can you explain this answer?
A circle of radius 6.5 cm is circumscribed around a right-angled triangle with the sides a, b and c cm where a, b and c are natural numbers. What is the perimeter of the triangle?
(2012)
a)
30 cm
b)
26 cm
c)
28 cm
d)
32 cm
|
|
Avinash Sharma answered |
Centre of the circle will be mid-point of the hypotenuse of the triangle.
So, hypotenuse = 2 × 6.5 = 13 cm.
According to Pythagorean triples.
other sides are 5 cm and 12 cm because all sides are natural number.
∴ So perimeter = 5 + 12 + 13 = 30 cm
So, hypotenuse = 2 × 6.5 = 13 cm.
According to Pythagorean triples.
other sides are 5 cm and 12 cm because all sides are natural number.
∴ So perimeter = 5 + 12 + 13 = 30 cm
A field is in the form of a rectangle of dimension 24 m × 56 m. There is 2700 m of fencing that is available. The field has to be divided into many identical smaller square plots, having integral sides (in metres), each of which is to be fenced. Find the side of each of the square plots such that the fencing material that is left out is minimum.(2015)- a)1 m
- b)2 m
- c)4 m
- d)8 m
Correct answer is option 'B'. Can you explain this answer?
A field is in the form of a rectangle of dimension 24 m × 56 m. There is 2700 m of fencing that is available. The field has to be divided into many identical smaller square plots, having integral sides (in metres), each of which is to be fenced. Find the side of each of the square plots such that the fencing material that is left out is minimum.
(2015)
a)
1 m
b)
2 m
c)
4 m
d)
8 m
|
Dia Mehta answered |
Here, HCF of 24 and 56 = 8 then, the side of the identical square plots = factors of 8.
The factors of 8 are 1, 2, 4 and 8
If side of the square plot is 1 m. the length of fencing material required is (25 × 56 + 57 × 24) = 2768 m
But 2768 m > 2700 m. (So, It is not possible)
If side of the square plot is 2 m. the length of fencing material required is
(29 × 24+13 × 56) =1464m < 2700 m
∴ minimum fencing material to be left the side of identical square plot = 2m.
The factors of 8 are 1, 2, 4 and 8
If side of the square plot is 1 m. the length of fencing material required is (25 × 56 + 57 × 24) = 2768 m
But 2768 m > 2700 m. (So, It is not possible)
If side of the square plot is 2 m. the length of fencing material required is
(29 × 24+13 × 56) =1464m < 2700 m
∴ minimum fencing material to be left the side of identical square plot = 2m.
A spherical ball of the maximum possible volume is placed inside a right-circular cone of height ‘h’ units. If the radius of the base of the cone is equal to h/ √3 units, then the ratio of the volume of the sphere to that of the cone is(2013)- a)4 : 9
- b)5 : 9
- c)1 : √3
- d)2 : 3√3
Correct answer is option 'A'. Can you explain this answer?
A spherical ball of the maximum possible volume is placed inside a right-circular cone of height ‘h’ units. If the radius of the base of the cone is equal to h/ √3 units, then the ratio of the volume of the sphere to that of the cone is
(2013)
a)
4 : 9
b)
5 : 9
c)
1 : √3
d)
2 : 3√3
|
Rohit Jain answered |
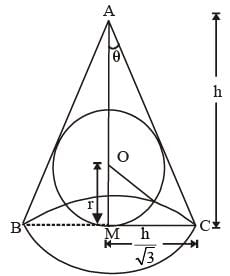
Let the semi vertical angle of the cone be θ.
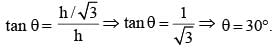
The vertical angle of the cone = 60°
Therefore, the triangle ABC is an equilateral triangle.
Therefore, the center (O) of the circle will coincide with the centroid of the triangle ABC.
In triangle ACM, OC is angle bisector of ∠ACM.
∴ ∠OCM = 30°
In ΔOCM,
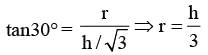
Hence, the ratio of the volume of the sphere to that of
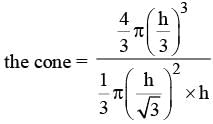
∴ Required ratio = 4 : 9
How many rectangles with integral sides are possible where the area of the rectangle equals the perimeter of the rectangle?(2014)- a)One
- b)Three
- c)Two
- d)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
How many rectangles with integral sides are possible where the area of the rectangle equals the perimeter of the rectangle?
(2014)
a)
One
b)
Three
c)
Two
d)
Infinitely many
|
Ananya Kaur answered |
There are two key pieces of information given in the question:
1. The area of the rectangle equals the perimeter of the rectangle.
2. The sides of the rectangle are integers.
To solve this question, we need to find the number of rectangles that satisfy both conditions.
Let's consider a rectangle with length L and width W. According to the given information, the area of the rectangle is LW, and the perimeter is 2(L + W).
From the first condition, we have LW = 2(L + W).
Rearranging this equation, we get LW - 2L - 2W = 0.
Using the Simon's Favorite Factoring Trick, we can rewrite this equation as (L - 2)(W - 2) = 4.
Now, we need to find all possible pairs of integers (L, W) such that their product is 4. These pairs are (1, 4), (2, 2), and (4, 1).
Let's analyze each pair separately:
1. For (1, 4): If L = 1 and W = 4, the perimeter is 2(1 + 4) = 10, which does not equal the area of the rectangle (1 * 4 = 4). Therefore, this pair does not satisfy the conditions.
2. For (2, 2): If L = 2 and W = 2, the perimeter is 2(2 + 2) = 8, which does equal the area of the rectangle (2 * 2 = 4). Therefore, this pair satisfies the conditions.
3. For (4, 1): If L = 4 and W = 1, the perimeter is 2(4 + 1) = 10, which does not equal the area of the rectangle (4 * 1 = 4). Therefore, this pair does not satisfy the conditions.
Therefore, there are two rectangles that satisfy the conditions: one with sides 2 and 2, and one with sides 2 and 2 (since it is a rectangle, the order of the sides does not matter).
Hence, the correct answer is option C: Two.
1. The area of the rectangle equals the perimeter of the rectangle.
2. The sides of the rectangle are integers.
To solve this question, we need to find the number of rectangles that satisfy both conditions.
Let's consider a rectangle with length L and width W. According to the given information, the area of the rectangle is LW, and the perimeter is 2(L + W).
From the first condition, we have LW = 2(L + W).
Rearranging this equation, we get LW - 2L - 2W = 0.
Using the Simon's Favorite Factoring Trick, we can rewrite this equation as (L - 2)(W - 2) = 4.
Now, we need to find all possible pairs of integers (L, W) such that their product is 4. These pairs are (1, 4), (2, 2), and (4, 1).
Let's analyze each pair separately:
1. For (1, 4): If L = 1 and W = 4, the perimeter is 2(1 + 4) = 10, which does not equal the area of the rectangle (1 * 4 = 4). Therefore, this pair does not satisfy the conditions.
2. For (2, 2): If L = 2 and W = 2, the perimeter is 2(2 + 2) = 8, which does equal the area of the rectangle (2 * 2 = 4). Therefore, this pair satisfies the conditions.
3. For (4, 1): If L = 4 and W = 1, the perimeter is 2(4 + 1) = 10, which does not equal the area of the rectangle (4 * 1 = 4). Therefore, this pair does not satisfy the conditions.
Therefore, there are two rectangles that satisfy the conditions: one with sides 2 and 2, and one with sides 2 and 2 (since it is a rectangle, the order of the sides does not matter).
Hence, the correct answer is option C: Two.
If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15 , then the ratio of the length of the shortest edge of the brick to that of its longest edge is(2019)- a)1 : √3
- b)√3 : 2
- c)√2 : √3
- d)2 : √5
Correct answer is option 'A'. Can you explain this answer?
If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15 , then the ratio of the length of the shortest edge of the brick to that of its longest edge is
(2019)
a)
1 : √3
b)
√3 : 2
c)
√2 : √3
d)
2 : √5
|
|
Rohit Jain answered |
Let the edges of the brick be a, b, and c such that
a < b < c
a2 + b2 = 32 = 9 ...(i)
a2 + c2 = ( 2√3 )2 = 12 ...(ii)
b2 + c2 = ( √15 )2 = 15 ...(iii)
Adding all three equations. We get
2(a2 + b2 + c2) = 9 + 12 + 15 = 36
a2 + b2 + c2 = 18 ...(iv)
From (i) and (iv), c2 = 18 – 9 ⇒ c = 3
From (iii) and (iv) a2 = 18 – 15 ⇒ a = 3
Therefore, required ratio =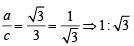
a < b < c
a2 + b2 = 32 = 9 ...(i)
a2 + c2 = ( 2√3 )2 = 12 ...(ii)
b2 + c2 = ( √15 )2 = 15 ...(iii)
Adding all three equations. We get
2(a2 + b2 + c2) = 9 + 12 + 15 = 36
a2 + b2 + c2 = 18 ...(iv)
From (i) and (iv), c2 = 18 – 9 ⇒ c = 3
From (iii) and (iv) a2 = 18 – 15 ⇒ a = 3
Therefore, required ratio =
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is(2018)- a)198
- b)200
- c)298
- d)100
Correct answer is option 'A'. Can you explain this answer?
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is
(2018)
a)
198
b)
200
c)
298
d)
100
|
|
Rajiv Reddy answered |
The radius of the cone is 4 feet.
The tip of the cone is a cone of height 3 feet.
By similarity, its radius is 1 foot.
The volume of the remaining part of the cone
= Volume of the cone – Volume of the tip of the cone
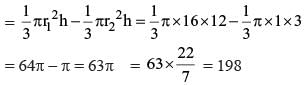
The tip of the cone is a cone of height 3 feet.
By similarity, its radius is 1 foot.
The volume of the remaining part of the cone
= Volume of the cone – Volume of the tip of the cone
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be(2018)- a)248√3
- b)192√3
- c)188√3
- d)1164√3
Correct answer is option 'B'. Can you explain this answer?
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be
(2018)
a)
248√3
b)
192√3
c)
188√3
d)
1164√3
|
|
Rohit Jain answered |
An equilateral triangle formed by joining the midpoints of the sides of a given equilateral triangle will have its side equal to half the side of the given equilateral triangle.
Now, side of T1 = 24 cm
Side of T2 = 12 cm
Side of T3 = 6 cm
and so on.
Sum of the areas of all the triangles =
Now, side of T1 = 24 cm
Side of T2 = 12 cm
Side of T3 = 6 cm
and so on.
Sum of the areas of all the triangles =
From a square piece of card-board measuring 2a on each side of a box with no top is to be formed by cutting out from each corner a square with sides b and bending up the flaps. The value of b for which the box has the greatest volume is(2011)- a)
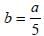
- b)
- c)
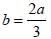
- d)
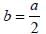
Correct answer is option 'C'. Can you explain this answer?
From a square piece of card-board measuring 2a on each side of a box with no top is to be formed by cutting out from each corner a square with sides b and bending up the flaps. The value of b for which the box has the greatest volume is
(2011)
a)
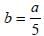
b)
c)
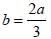
d)
|
|
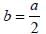
Rohit Jain answered |
Since cubic shape will be the greatest volume (as volume = side3)
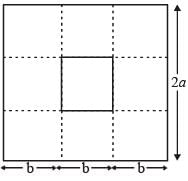
Hence, 3b = 2a
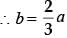
Hence, 3b = 2a
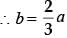
A trapezium DEFG is circumscribed about a circle that has centre at C. If DM = 1 cm, GN = 4 cm and the measure of ∠DEF = ∠EFG = 90°, then find the radius of the circle.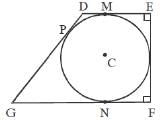
(2012)- a)2 cm
- b)2.5 cm
- c)2.25 cm
- d)4 cm
Correct answer is option 'A'. Can you explain this answer?
A trapezium DEFG is circumscribed about a circle that has centre at C. If DM = 1 cm, GN = 4 cm and the measure of ∠DEF = ∠EFG = 90°, then find the radius of the circle.
(2012)
a)
2 cm
b)
2.5 cm
c)
2.25 cm
d)
4 cm
|
|
Lavanya Menon answered |
Let, the radius of circle be 'x' cm.
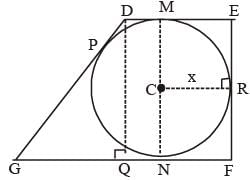
∴ CM = CN = CR = x
Given that GN = 4 cm
∴ GP = 4 cm
Also, DP = DM = QN = 1 cm
∴ GD = 5 cm
GQ = GN – QN = 4 – 1 = 3 cm
In ΔDGQ : DQ =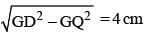
⇒ 2x = 4 cm (∵ DQ = MN)
∴ x = 2 cm
∴ radius or circle = 2 cm
∴ CM = CN = CR = x
Given that GN = 4 cm
∴ GP = 4 cm
Also, DP = DM = QN = 1 cm
∴ GD = 5 cm
GQ = GN – QN = 4 – 1 = 3 cm
In ΔDGQ : DQ =
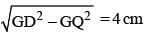
⇒ 2x = 4 cm (∵ DQ = MN)
∴ x = 2 cm
∴ radius or circle = 2 cm
The length of the hypotenuse of a right-angled triangle is 240 units. The perimeter of the given triangle is a perfect square. If the perimeter of the given triangle is greater than 550 units, then which of the following can be the length of a side of the given right-angled triangle?(2014)- a)192 units
- b)168 units
- c)144 units
- d)Both (a) and (c)
Correct answer is option 'D'. Can you explain this answer?
The length of the hypotenuse of a right-angled triangle is 240 units. The perimeter of the given triangle is a perfect square. If the perimeter of the given triangle is greater than 550 units, then which of the following can be the length of a side of the given right-angled triangle?
(2014)
a)
192 units
b)
168 units
c)
144 units
d)
Both (a) and (c)
|
|
Lavanya Menon answered |
Let the length of the other two sides of the triangle be 'x' and 'y' respectively. then,
x2 + y2 = (240)2 (hypotenuse of triangle = 240)
Also, x + y + 240 must be perfect square (because perimeter of triangle is perfect square).
When the two sides other than hypotenuse are equal length than perimeter of right angled triangle is maximized.
Therefore,
The maximum perimeter of right angled triangle
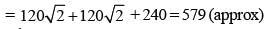
Also,
The perimeter of triangle should be greater than twice the length of hypotenuse of triangle.
Then, the perimeter of triangle should be greater than 480 and less than 579. according to question.
Perimeter of triangle should be 484, 529 and 576
(because perimeter is perfect square)
Again, according to question, Perimeter of triangle is greater than 550, So perimeter = 576.
Here, perimeter of triangle = 576.
According to pythogorean triples.
The value of x and y will be 192 and 144 units.
x2 + y2 = (240)2 (hypotenuse of triangle = 240)
Also, x + y + 240 must be perfect square (because perimeter of triangle is perfect square).
When the two sides other than hypotenuse are equal length than perimeter of right angled triangle is maximized.
Therefore,
The maximum perimeter of right angled triangle
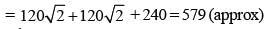
Also,
The perimeter of triangle should be greater than twice the length of hypotenuse of triangle.
Then, the perimeter of triangle should be greater than 480 and less than 579. according to question.
Perimeter of triangle should be 484, 529 and 576
(because perimeter is perfect square)
Again, according to question, Perimeter of triangle is greater than 550, So perimeter = 576.
Here, perimeter of triangle = 576.
According to pythogorean triples.
The value of x and y will be 192 and 144 units.
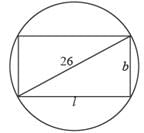
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?(2018)- a)25, 9
- b)24, 12
- c)24, 10
- d)25, 10
Correct answer is option 'C'. Can you explain this answer?
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
(2018)
a)
25, 9
b)
24, 12
c)
24, 10
d)
25, 10
|
|
Amit Kumar answered |
Let the length and the breadth of the rectangle be l and b respectively.
Diameter of the circle = Diagonal of the rectangle
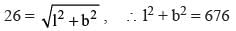
Hence, possible values of l and b are 24 and 10 respectively.
Diameter of the circle = Diagonal of the rectangle
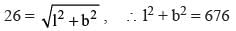
Hence, possible values of l and b are 24 and 10 respectively.
In the regular hexagon shown below, what is the ratio of the area of the smaller circle to that of the bigger circle?
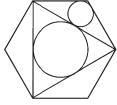(2012)- a)3 : 7 + 2√3
- b)3 : 7 + √3
- c)3 : 16 + 4√3
- d)3 : 7 + 4√3
Correct answer is option 'D'. Can you explain this answer?
In the regular hexagon shown below, what is the ratio of the area of the smaller circle to that of the bigger circle?
(2012)
a)
3 : 7 + 2√3
b)
3 : 7 + √3
c)
3 : 16 + 4√3
d)
3 : 7 + 4√3
|
|
Rishika Sengupta answered |
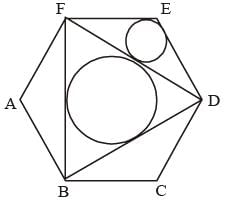
Let EF = s unit
In Δ DEF : DF = 2EF cos30° = √3s
Semi perimeter of D DEF (in units) = S
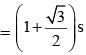
Area of Δ DEF (in unit2 = Δ
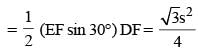
Inradius of Δ DEF (in units) = r2
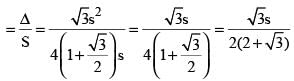
In radius of triangle DEF (in units) = r2
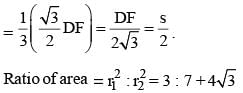
Chapter doubts & questions for Mensuration: Cylinder, Cone and Sphere - Mathematics Class 10 ICSE 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration: Cylinder, Cone and Sphere - Mathematics Class 10 ICSE in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics Class 10 ICSE
74 videos|198 docs|30 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily