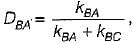All Exams >
Civil Engineering (CE) >
Structural Analysis >
All Questions
All questions of Determinacy & Indeterminacy of Structures for Civil Engineering (CE) Exam
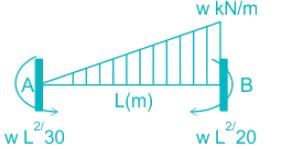
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is
- a)12
- b)14
- c)20
- d)22
Correct answer is option 'B'. Can you explain this answer?
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is


a)
12
b)
14
c)
20
d)
22

|
Engineers Adda answered |
j = 11; r=8; m=11
Dk = 3j-r-no. of inextensible members = 3(11) – 8 -11 = 14
Dk = 3j-r-no. of inextensible members = 3(11) – 8 -11 = 14
Which one of the following statements is correct? The principle of superposition is applicable to- a)nonlinear behaviour of material and small displacement theory.
- b)nonlinear behaviour of material and large displacement theory.
- c)linear elastic behaviour of material and small displacement theory.
- d)linear elastic behaviour of material and large displacement theory.
Correct answer is option 'C'. Can you explain this answer?
Which one of the following statements is correct? The principle of superposition is applicable to
a)
nonlinear behaviour of material and small displacement theory.
b)
nonlinear behaviour of material and large displacement theory.
c)
linear elastic behaviour of material and small displacement theory.
d)
linear elastic behaviour of material and large displacement theory.
|
|
Lavanya Menon answered |
The principle of superposition states that the displacements resulting from each of a number of forces may be added to obtain the displacements resulting from the sum of forces. This method depends upon the linearity of the governing relations between the load and deflection, The linearity depends upon two factors.
(i) the linearity between bending moment and curvature which depends upon the linear elastic materials In non-linear material superposition of curvatures is not possible.
(ii) the linearity between curvatures and deflection depends upon the assumption that the deflections are so small that the approximate curvature can be used in place of true curvature.
(i) the linearity between bending moment and curvature which depends upon the linear elastic materials In non-linear material superposition of curvatures is not possible.
(ii) the linearity between curvatures and deflection depends upon the assumption that the deflections are so small that the approximate curvature can be used in place of true curvature.
Roller support is same as _____- a)Hinged support
- b)Fixed support
- c)Simply support
- d)Roller support
Correct answer is option 'C'. Can you explain this answer?
Roller support is same as _____
a)
Hinged support
b)
Fixed support
c)
Simply support
d)
Roller support

|
Subham Unni answered |
Simply supported
A roller support is the same as a simply supported beam in structural engineering. This type of support allows for vertical movement at the point of contact, similar to a roller moving along a surface.
Characteristics of roller support:
- It only restricts vertical movement, allowing for horizontal movement and rotation.
- It provides a reaction force that is perpendicular to the surface.
- It is commonly used in situations where thermal expansion or contraction needs to be accommodated.
Comparison with other types of supports:
- Unlike a hinged support, a roller support does not restrict rotational movement.
- Unlike a fixed support, a roller support does not restrict horizontal movement.
Applications of roller support:
- Roller supports are commonly used in bridges, where expansion and contraction due to temperature changes need to be accommodated.
- They are also used in conveyor systems and other structures where movement is required.
In conclusion, a roller support is similar to a simply supported beam in that it allows for vertical movement while providing a reaction force perpendicular to the surface. It is a versatile type of support that is used in various engineering applications.
A simple support offers only _______ reaction normal to the axis of the beam.- a)Horizontal
- b)Vertical
- c)Inclined
- d)Moment
Correct answer is option 'B'. Can you explain this answer?
A simple support offers only _______ reaction normal to the axis of the beam.
a)
Horizontal
b)
Vertical
c)
Inclined
d)
Moment
|
|
Sudhir Patel answered |
In a simple support there will not be any resistance to horizontal loads, moment or rotation. In fact, it only offers a vertical reaction normal to the axis of the beam.
For a simply supported beam, the moment at the support is always __________- a)Maximum
- b)Zero
- c)Minimum
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
For a simply supported beam, the moment at the support is always __________
a)
Maximum
b)
Zero
c)
Minimum
d)
Cannot be determined
|
|
Sudhir Patel answered |
As the moment is a product of force and perpendicular distance, the flexural moment at the support is zero because there is no distance at the support.
The degree of freedom of a joint for the rigid jointed joint plane frame is _____- a)0
- b)2
- c)3
- d)6
Correct answer is option 'C'. Can you explain this answer?
The degree of freedom of a joint for the rigid jointed joint plane frame is _____
a)
0
b)
2
c)
3
d)
6

|
Alok Iyer answered |
The degree of freedom of a joint refers to the number of independent motions or directions in which the joint can move. In the case of a rigid jointed joint plane frame, the degree of freedom can be determined by considering the constraints and restrictions imposed by the joint connections.
Rigid Jointed Joint Plane Frame:
A rigid jointed joint plane frame consists of a series of members connected at their ends by joints. These joints are assumed to be perfectly rigid, meaning that they do not allow any relative movement between the connected members. The frame is typically constructed by welding or bolting the members together at the joints.
Degree of Freedom:
The degree of freedom of a joint in a rigid jointed joint plane frame can be determined using the equation:
DOF = 6 - R - 2J
Where:
DOF = Degree of Freedom
R = Number of reactions or constraints at the joint
J = Number of members meeting at the joint
Explanation:
1. Reactions (R):
The number of reactions at a joint depends on the support conditions. A joint may have both translational and rotational reactions. In a two-dimensional plane frame, each joint can have a maximum of three reactions: two translations (horizontal and vertical) and one rotation. However, the number of reactions can be less if the joint is fully restrained or partially restrained.
2. Members (J):
The number of members meeting at a joint represents the connections between the members. Each member provides two degrees of freedom at the joint, one for each end. Therefore, the total number of degrees of freedom contributed by the members meeting at a joint is equal to twice the number of members.
By subtracting the number of reactions (R) and twice the number of members (2J) from 6, we can determine the degree of freedom (DOF) at the joint.
In the case of a rigid jointed joint plane frame, the joints are assumed to be fully restrained, meaning that all three reactions (R) are present at each joint. Additionally, each joint is connected to two members (J). Substituting these values into the equation, we have:
DOF = 6 - R - 2J
DOF = 6 - 3 - 2(2)
DOF = 6 - 3 - 4
DOF = 3
Therefore, the degree of freedom of a joint for a rigid jointed joint plane frame is 3 (option C).
Rigid Jointed Joint Plane Frame:
A rigid jointed joint plane frame consists of a series of members connected at their ends by joints. These joints are assumed to be perfectly rigid, meaning that they do not allow any relative movement between the connected members. The frame is typically constructed by welding or bolting the members together at the joints.
Degree of Freedom:
The degree of freedom of a joint in a rigid jointed joint plane frame can be determined using the equation:
DOF = 6 - R - 2J
Where:
DOF = Degree of Freedom
R = Number of reactions or constraints at the joint
J = Number of members meeting at the joint
Explanation:
1. Reactions (R):
The number of reactions at a joint depends on the support conditions. A joint may have both translational and rotational reactions. In a two-dimensional plane frame, each joint can have a maximum of three reactions: two translations (horizontal and vertical) and one rotation. However, the number of reactions can be less if the joint is fully restrained or partially restrained.
2. Members (J):
The number of members meeting at a joint represents the connections between the members. Each member provides two degrees of freedom at the joint, one for each end. Therefore, the total number of degrees of freedom contributed by the members meeting at a joint is equal to twice the number of members.
By subtracting the number of reactions (R) and twice the number of members (2J) from 6, we can determine the degree of freedom (DOF) at the joint.
In the case of a rigid jointed joint plane frame, the joints are assumed to be fully restrained, meaning that all three reactions (R) are present at each joint. Additionally, each joint is connected to two members (J). Substituting these values into the equation, we have:
DOF = 6 - R - 2J
DOF = 6 - 3 - 2(2)
DOF = 6 - 3 - 4
DOF = 3
Therefore, the degree of freedom of a joint for a rigid jointed joint plane frame is 3 (option C).
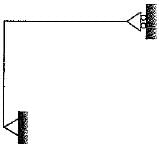
The rigid-jointed frame shown in the figure is
- a)unstable
- b)stable and statically determinate
- c)stable and statically indeterminate by one degree
- d)stable and statically indeterminate by two degree
Correct answer is option 'B'. Can you explain this answer?
The rigid-jointed frame shown in the figure is


a)
unstable
b)
stable and statically determinate
c)
stable and statically indeterminate by one degree
d)
stable and statically indeterminate by two degree

|
Sanjay Gp answered |
For a rigid joined 2D frame structure. Degree of static indeterminacy
Ds=3m+r-3j
here
Ds=3x2+3-3x3=0.
Hence it is statically determinate.
And since reactions are not parallel or concurrent it is a stable member.
Ds=3m+r-3j
here
Ds=3x2+3-3x3=0.
Hence it is statically determinate.
And since reactions are not parallel or concurrent it is a stable member.
A uniform simply supported beam is subjected to a clockwise moment M at the left end. What is the moment required at the right end so that rotation of the right end is zero?- a)2M
- b)M
- c)M/2
- d)M/3
Correct answer is option 'C'. Can you explain this answer?
A uniform simply supported beam is subjected to a clockwise moment M at the left end. What is the moment required at the right end so that rotation of the right end is zero?
a)
2M
b)
M
c)
M/2
d)
M/3

|
Garima Kulkarni answered |
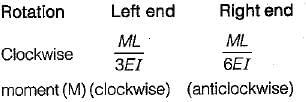
at left end
To keep rotation at right and zero a moment should be applied in anticlockwise direction. Let the moment in M'

“Hinged support offers resistance against rotation”.- a)True
- b)False
- c)Cannot be determined
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
“Hinged support offers resistance against rotation”.
a)
True
b)
False
c)
Cannot be determined
d)
None of the above
|
|
Sudhir Patel answered |
A hinged support offers resistance against horizontal and vertical movement but not against rotation. It support offers a vertical and horizontal reaction only.
________ support develops support moment.- a)Hinged
- b)Simple
- c)Fixed
- d)Joint
Correct answer is option 'C'. Can you explain this answer?
________ support develops support moment.
a)
Hinged
b)
Simple
c)
Fixed
d)
Joint
|
|
Sudhir Patel answered |
A fixed support offers resistance against horizontal and vertical movement and against the rotation of the member and that in turn developers support moment.
A single-bay, single-storeyed portal frame ABCD has its column ends fixed. If axial deformation is neglected, the kinematic indeterminacy is- a)3
- b)2
- c)6
- d)4
Correct answer is option 'A'. Can you explain this answer?
A single-bay, single-storeyed portal frame ABCD has its column ends fixed. If axial deformation is neglected, the kinematic indeterminacy is
a)
3
b)
2
c)
6
d)
4

|
Sreemoyee Joshi answered |
Problem Analysis
We are given a single-bay, single-storeyed portal frame ABCD with fixed column ends. We need to determine the kinematic indeterminacy of the frame.
Solution
The kinematic indeterminacy of a structure refers to the number of redundant members or joints that can be removed without causing any change in the stability or equilibrium of the structure.
In the given portal frame, the column ends are fixed, which means they are fully restrained against rotation and translation. This implies that there is no relative rotation or displacement between the column ends and the foundation.
Analysis of the Frame
To determine the kinematic indeterminacy, we need to analyze the frame and identify the degrees of freedom.
1. Number of Joints (J): In the given frame, there are four joints: A, B, C, and D.
2. Number of Members (M): There are three members: AB, BC, and CD.
Degree of Freedom Analysis
Next, we analyze the degrees of freedom at each joint to determine the kinematic indeterminacy.
1. Joint A:
- Vertical Displacement (V): Since the column end is fixed, there is no vertical displacement at joint A.
- Horizontal Displacement (H): Since the column end is fixed, there is no horizontal displacement at joint A.
- Rotation (R): Since the column end is fixed, there is no rotation at joint A.
- Total Degrees of Freedom (DOF) at Joint A: 0
2. Joint B:
- Vertical Displacement (V): The vertical displacement at joint B is not restricted as it is connected to the member AB.
- Horizontal Displacement (H): The horizontal displacement at joint B is not restricted as it is connected to the member AB.
- Rotation (R): The rotation at joint B is not restricted as it is connected to the member AB.
- Total Degrees of Freedom (DOF) at Joint B: 3
3. Joint C:
- Vertical Displacement (V): The vertical displacement at joint C is not restricted as it is connected to the member BC.
- Horizontal Displacement (H): The horizontal displacement at joint C is not restricted as it is connected to the member BC.
- Rotation (R): The rotation at joint C is not restricted as it is connected to the member BC.
- Total Degrees of Freedom (DOF) at Joint C: 3
4. Joint D:
- Vertical Displacement (V): Since the column end is fixed, there is no vertical displacement at joint D.
- Horizontal Displacement (H): Since the column end is fixed, there is no horizontal displacement at joint D.
- Rotation (R): Since the column end is fixed, there is no rotation at joint D.
- Total Degrees of Freedom (DOF) at Joint D: 0
Kinematic Indeterminacy Calculation
The kinematic indeterminacy is given by the formula:
I = 3J - 2M - R
where I is the kinematic indeterminacy, J is the number of joints, M is the number of members, and R is the number of support reactions.
In this case, there are no support reactions (R = 0) as the column ends are fixed.
Substituting the values, we have:
I = 3(4)
We are given a single-bay, single-storeyed portal frame ABCD with fixed column ends. We need to determine the kinematic indeterminacy of the frame.
Solution
The kinematic indeterminacy of a structure refers to the number of redundant members or joints that can be removed without causing any change in the stability or equilibrium of the structure.
In the given portal frame, the column ends are fixed, which means they are fully restrained against rotation and translation. This implies that there is no relative rotation or displacement between the column ends and the foundation.
Analysis of the Frame
To determine the kinematic indeterminacy, we need to analyze the frame and identify the degrees of freedom.
1. Number of Joints (J): In the given frame, there are four joints: A, B, C, and D.
2. Number of Members (M): There are three members: AB, BC, and CD.
Degree of Freedom Analysis
Next, we analyze the degrees of freedom at each joint to determine the kinematic indeterminacy.
1. Joint A:
- Vertical Displacement (V): Since the column end is fixed, there is no vertical displacement at joint A.
- Horizontal Displacement (H): Since the column end is fixed, there is no horizontal displacement at joint A.
- Rotation (R): Since the column end is fixed, there is no rotation at joint A.
- Total Degrees of Freedom (DOF) at Joint A: 0
2. Joint B:
- Vertical Displacement (V): The vertical displacement at joint B is not restricted as it is connected to the member AB.
- Horizontal Displacement (H): The horizontal displacement at joint B is not restricted as it is connected to the member AB.
- Rotation (R): The rotation at joint B is not restricted as it is connected to the member AB.
- Total Degrees of Freedom (DOF) at Joint B: 3
3. Joint C:
- Vertical Displacement (V): The vertical displacement at joint C is not restricted as it is connected to the member BC.
- Horizontal Displacement (H): The horizontal displacement at joint C is not restricted as it is connected to the member BC.
- Rotation (R): The rotation at joint C is not restricted as it is connected to the member BC.
- Total Degrees of Freedom (DOF) at Joint C: 3
4. Joint D:
- Vertical Displacement (V): Since the column end is fixed, there is no vertical displacement at joint D.
- Horizontal Displacement (H): Since the column end is fixed, there is no horizontal displacement at joint D.
- Rotation (R): Since the column end is fixed, there is no rotation at joint D.
- Total Degrees of Freedom (DOF) at Joint D: 0
Kinematic Indeterminacy Calculation
The kinematic indeterminacy is given by the formula:
I = 3J - 2M - R
where I is the kinematic indeterminacy, J is the number of joints, M is the number of members, and R is the number of support reactions.
In this case, there are no support reactions (R = 0) as the column ends are fixed.
Substituting the values, we have:
I = 3(4)
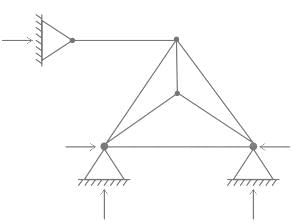
Find the degree of static indeterminacy, for a two dimensional truss (or frame) shown in the figure above.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?

Find the degree of static indeterminacy, for a two dimensional truss (or frame) shown in the figure above.
a)
1
b)
2
c)
3
d)
4

|
Pioneer Academy answered |
Concept:
If the number of unknown reaction are more than the number of equilibrium equation available then structure is called indeterminate structure and degree of indeterminacy is given by static indeterminacy.
Some important cases are:
If the number of unknown reaction are more than the number of equilibrium equation available then structure is called indeterminate structure and degree of indeterminacy is given by static indeterminacy.
Some important cases are:
- Pin jointed plane frame, Ds = m + r - 2j
- Pin joined space frame, Ds = m + r - 3j
- Rigid jointed plane frame, Ds = 3m + r - 3j
- Rigid jointed space frame, Ds = 6m + r - 6j
Where,
m = number of members
r = number of external reactions
j = number of joints.
Data Given by the figure,
m = 7
r = 6
J = 5
We know that,
For pin jointed plane frame: Ds = m + r - 2J
Ds = 7 + 6 - 2 x 5
Ds = 3
m = number of members
r = number of external reactions
j = number of joints.
Data Given by the figure,
m = 7
r = 6
J = 5
We know that,
For pin jointed plane frame: Ds = m + r - 2J
Ds = 7 + 6 - 2 x 5
Ds = 3
A pin-jointed plane frame is unstable if where m is number of members r is reaction components and j is number of joints- a)(m + r) < 2j
- b)m + r = 2j
- c)(m + r)> 2j
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A pin-jointed plane frame is unstable if where m is number of members r is reaction components and j is number of joints
a)
(m + r) < 2j
b)
m + r = 2j
c)
(m + r)> 2j
d)
None of these

|
Sparsh Unni answered |
>j+2
Explanation:
For a pin-jointed plane frame to be stable, it must satisfy the condition of static equilibrium, which is that the sum of all forces and moments acting on the frame is zero. In other words, the number of unknown forces and moments must be equal to the number of equations of static equilibrium (i.e. three equations for a 2D frame).
In a pin-jointed plane frame, each joint can provide two equilibrium equations (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of equations of equilibrium is 2j.
On the other hand, each member can carry one unknown force (either tension or compression). Therefore, the total number of unknown forces is m.
Finally, the reaction components at the supports can be expressed using two equations of equilibrium (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of unknown reaction components is r.
So, by applying the principle of statics, we can write the following equation for stability of a pin-jointed plane frame:
m + r = 2j
Simplifying this equation, we get:
m - 2j + r = 0
Therefore, for a pin-jointed plane frame to be stable, the expression (m - 2j + r) must be equal to zero. However, for instability, this expression must be greater than zero.
Hence, the condition for instability can be expressed as:
m - 2j + r > 0
or equivalently,
m > 2j - r
Adding 2 to both sides, we get:
m + 2 > 2j - r + 2
which can be rewritten as:
(m + r) > 2(j + 1)
or simply:
(m + r) > 2j + 2
Therefore, the condition for instability in a pin-jointed plane frame is:
(m + r) > 2j + 2.
Explanation:
For a pin-jointed plane frame to be stable, it must satisfy the condition of static equilibrium, which is that the sum of all forces and moments acting on the frame is zero. In other words, the number of unknown forces and moments must be equal to the number of equations of static equilibrium (i.e. three equations for a 2D frame).
In a pin-jointed plane frame, each joint can provide two equilibrium equations (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of equations of equilibrium is 2j.
On the other hand, each member can carry one unknown force (either tension or compression). Therefore, the total number of unknown forces is m.
Finally, the reaction components at the supports can be expressed using two equations of equilibrium (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of unknown reaction components is r.
So, by applying the principle of statics, we can write the following equation for stability of a pin-jointed plane frame:
m + r = 2j
Simplifying this equation, we get:
m - 2j + r = 0
Therefore, for a pin-jointed plane frame to be stable, the expression (m - 2j + r) must be equal to zero. However, for instability, this expression must be greater than zero.
Hence, the condition for instability can be expressed as:
m - 2j + r > 0
or equivalently,
m > 2j - r
Adding 2 to both sides, we get:
m + 2 > 2j - r + 2
which can be rewritten as:
(m + r) > 2(j + 1)
or simply:
(m + r) > 2j + 2
Therefore, the condition for instability in a pin-jointed plane frame is:
(m + r) > 2j + 2.
Degree of kinematic indeterminacy of a pin jointed plane frame is given by- a)2j – r
- b)j – 2r
- c)3j – r
- d)2j + r
Correct answer is option 'A'. Can you explain this answer?
Degree of kinematic indeterminacy of a pin jointed plane frame is given by
a)
2j – r
b)
j – 2r
c)
3j – r
d)
2j + r

|
Akanksha Mehta answered |
The degree of kinematic indeterminacy of a pin-jointed plane frame can be calculated using the formula:
Degree of Kinematic Indeterminacy = 3j - 2m
Where j is the total number of joints in the frame and m is the total number of members in the frame.
Since a pin-jointed plane frame is a 2D structure, we can assume that there are 3 reactions at each support (2 vertical and 1 horizontal). Therefore, the total number of reactions (m) is equal to 3 times the number of supports.
Hence, the formula for the degree of kinematic indeterminacy of a pin-jointed plane frame is:
Degree of Kinematic Indeterminacy = 3j - 6
Therefore, the given statement "Degree of kinematic indeterminacy of a pin jointed plane frame is given by 2j" is incorrect.
Degree of Kinematic Indeterminacy = 3j - 2m
Where j is the total number of joints in the frame and m is the total number of members in the frame.
Since a pin-jointed plane frame is a 2D structure, we can assume that there are 3 reactions at each support (2 vertical and 1 horizontal). Therefore, the total number of reactions (m) is equal to 3 times the number of supports.
Hence, the formula for the degree of kinematic indeterminacy of a pin-jointed plane frame is:
Degree of Kinematic Indeterminacy = 3j - 6
Therefore, the given statement "Degree of kinematic indeterminacy of a pin jointed plane frame is given by 2j" is incorrect.
The degree of freedom for the vertical guided roller is ________- a)0
- b)1
- c)2
- d)3
Correct answer is option 'B'. Can you explain this answer?
The degree of freedom for the vertical guided roller is ________
a)
0
b)
1
c)
2
d)
3
|
|
Anjana Singh answered |
Vertical guided roller resists horizontal/axial force and bending moment. However, it cannot resist vertical forces as it slides down along the plane. Hence it has 1 degree of freedom.

The degree of static indeterminacy of a pin- jointed space frame is given by- a)m + r - 2j
- b)m + r - 3j
- c)3m + r - 3j
- d)m + r + 3j
Correct answer is option 'B'. Can you explain this answer?
The degree of static indeterminacy of a pin- jointed space frame is given by
a)
m + r - 2j
b)
m + r - 3j
c)
3m + r - 3j
d)
m + r + 3j
|
|
Aditya Deshmukh answered |
Concept:
Static indeterminacy is the difference between a total number of unknowns (Total member forces+ reactions) and the total number of available equations from equilibrium conditions.
So for a pin-jointed frame total number of equations available at a joint = 2
So for j number of joints, equations available = 2j
So the degree of static indeterminacy of pin-jointed plane frame = m + r - 2j
Similarly, the DSI for pin jointed space frame = m + r - 3j
If the degree of static indeterminacy = 0, it is known as a statically determinate structure.
If the degree of static indeterminacy > 0, it is known as a statically indeterminate structure.
Degree of kinematic indeterminacy of a pin jointed plane frame is given by where j is number of joints and r is reaction components.- a)2j - r
- b)j - 2 r
- c)3j - r
- d)2j + r
Correct answer is option 'A'. Can you explain this answer?
Degree of kinematic indeterminacy of a pin jointed plane frame is given by where j is number of joints and r is reaction components.
a)
2j - r
b)
j - 2 r
c)
3j - r
d)
2j + r

|
Shilpa Pillai answered |
Dk = 2j –r for a pin jointed frame
Dk = 3j –r for a rigid jointed frame
j number of joints and r number of reactions.
Dk = 3j –r for a rigid jointed frame
j number of joints and r number of reactions.
If there are m unknown member forces, r unknown reaction components and j number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by- a)m + r + 2j
- b)m - r + 2j
- c)m + r-2'j
- d)m + r- 3j
Correct answer is option 'C'. Can you explain this answer?
If there are m unknown member forces, r unknown reaction components and j number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by
a)
m + r + 2j
b)
m - r + 2j
c)
m + r-2'j
d)
m + r- 3j

|
Anand Mehta answered |
Ds for a pin jointed frame = m+r-2j
Ds for a rigid jointed frame = 3m+r -3j
m- No. of members, r- no. of reactions, j- no. of joints
Ds for a rigid jointed frame = 3m+r -3j
m- No. of members, r- no. of reactions, j- no. of joints
Consider the following statements:
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacyWhich of these statements is correct?- a)1 and 3
- b)2 and 3
- c)1 and 4
- d)2 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements:
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacy
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacy
Which of these statements is correct?
a)
1 and 3
b)
2 and 3
c)
1 and 4
d)
2 and 4

|
Anagha Mehta answered |
Force method is useful when,
Ds < Dk
Displacement method is useful when,
Dk < Ds
Ds < Dk
Displacement method is useful when,
Dk < Ds
The degree of freedom for a rigid jointed plane frame without axial deformation is given by 3j – m – r.- a)True
- b)False
- c)Cannot be determined
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The degree of freedom for a rigid jointed plane frame without axial deformation is given by 3j – m – r.
a)
True
b)
False
c)
Cannot be determined
d)
None of the above

|
Gitanjali Chauhan answered |
The degree of freedom for a rigid jointed plane frame without axial deformation is given by 3j, where "j" represents the number of joints in the frame.
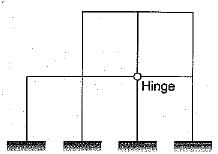
Total degree of indeterminacy (both internal and external) of the plane frame shown in the given figure is
- a)10
- b)11
- c)12
- d)15
Correct answer is option 'C'. Can you explain this answer?
Total degree of indeterminacy (both internal and external) of the plane frame shown in the given figure is


a)
10
b)
11
c)
12
d)
15

|
Swati Gupta answered |
The degree of indeterminacy,
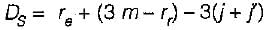
Number of external reactions = re
= 3 + 3 + 3 + 3 = 12
Number of rigid joints,
j= 10
Number of joints at which releases are located,
j= 1
Number of members,
m = 12
As the hinge is located at a point where 4 members meet. Hence it is equivalent to three hinges.
Therefore number of releases, rr = 3.
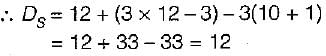
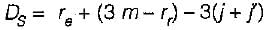
Number of external reactions = re
= 3 + 3 + 3 + 3 = 12
Number of rigid joints,
j= 10
Number of joints at which releases are located,
j= 1
Number of members,
m = 12
As the hinge is located at a point where 4 members meet. Hence it is equivalent to three hinges.
Therefore number of releases, rr = 3.
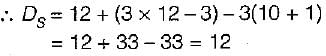
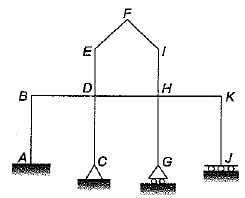
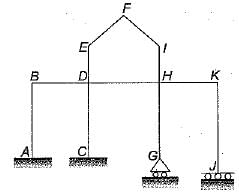
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is:
- a)12
- b)14
- c)20
- d)22
Correct answer is option 'B'. Can you explain this answer?
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is:


a)
12
b)
14
c)
20
d)
22

|
Shilpa Pillai answered |
Kinematic indeterminacy means degree of freedom of structure at various joints.
No rotation or translation is possible at A so degree of freedom at A is zero. There is a possibility of rotation at C but no translation so degree of freedom is one. At G both rotation and translation is possible so. degree of freedom is 2. At J no rotation but translation so d.o.f. is 1 . At B, D, H and K there are 4 rotations and 1 translation so d.o.f. is 5. At E, F and I three rotations and two translations so d.o.f., is 5.
So kinematic indeterminacy,
= 0 + 1 + 2 + 1 + 5 + 5 = 14
Alternate:
From direct formula
External reactions re = 3 + 2 + 1 + 2 = 8
Number of members (m) = 11
Number of rigid joints (j) = 9
Number of hinged joints (j') = 2
There are no internal hinges so number of releases is zero.
rr = 0
Degree of kinematic indeterminacy,
Dk = 3(j + j') - re + rr - m
= 3 x (9 + 2) - 8 - 11
= 33 - 19 = 14
No rotation or translation is possible at A so degree of freedom at A is zero. There is a possibility of rotation at C but no translation so degree of freedom is one. At G both rotation and translation is possible so. degree of freedom is 2. At J no rotation but translation so d.o.f. is 1 . At B, D, H and K there are 4 rotations and 1 translation so d.o.f. is 5. At E, F and I three rotations and two translations so d.o.f., is 5.
So kinematic indeterminacy,
= 0 + 1 + 2 + 1 + 5 + 5 = 14
Alternate:
From direct formula
External reactions re = 3 + 2 + 1 + 2 = 8
Number of members (m) = 11
Number of rigid joints (j) = 9
Number of hinged joints (j') = 2
There are no internal hinges so number of releases is zero.
rr = 0
Degree of kinematic indeterminacy,
Dk = 3(j + j') - re + rr - m
= 3 x (9 + 2) - 8 - 11
= 33 - 19 = 14
Hinge support is called as __________- a)Socket joint
- b)Swivel joint
- c)Ball joint
- d)Pin joint
Correct answer is option 'D'. Can you explain this answer?
Hinge support is called as __________
a)
Socket joint
b)
Swivel joint
c)
Ball joint
d)
Pin joint
|
|
Sudhir Patel answered |
Hinge support is one, in which the position is fixed but not the direction. In their words hinged support offers resistance against vertical and horizontal moments.it is fixed in such a way that it resembles like a pin joint.
What is the degree of kinematic indeterminacy of the beam shown in figure above- a)2
- b)3
- c)5
- d)9
Correct answer is option 'C'. Can you explain this answer?

What is the degree of kinematic indeterminacy of the beam shown in figure above
a)
2
b)
3
c)
5
d)
9
|
|
Anjana Singh answered |
Concept:
Degree of Kinematic Indeterminacy:
Degree of kinematic indeterminacy (Dk) refers to the total number of independent available degree of freedom of all joints. The degree of kinematic indeterminacy may be defined as the total number of unrestrained displacement component of all joints.
Degree of kinematic indeterminacy for rigid jointed plane frame and beam is given by,
Dk = 3j - re
Where, j = Number of joint, re = Number of external recation
Degree of Kinematic Indeterminacy:
Degree of kinematic indeterminacy (Dk) refers to the total number of independent available degree of freedom of all joints. The degree of kinematic indeterminacy may be defined as the total number of unrestrained displacement component of all joints.
Degree of kinematic indeterminacy for rigid jointed plane frame and beam is given by,
Dk = 3j - re
Where, j = Number of joint, re = Number of external recation
Calculation:
Degree of kinematic indeterminacy (Dk) = 3j - re
Here, j = 3 and re = 4
Dk = 3 × 3 - 4 = 5
Degree of kinematic indeterminacy (Dk) = 3j - re
Here, j = 3 and re = 4
Dk = 3 × 3 - 4 = 5
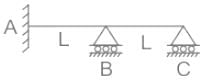
A continuous beam ABC with span AB = BC = L is shown in the figure. Supports A is fixed type, and supports B and C are roller type. The kinematic indeterminacy of the beam is:
- a)5
- b)3
- c)2
- d)4
Correct answer is option 'D'. Can you explain this answer?
A continuous beam ABC with span AB = BC = L is shown in the figure. Supports A is fixed type, and supports B and C are roller type. The kinematic indeterminacy of the beam is:


a)
5
b)
3
c)
2
d)
4

|
Pioneer Academy answered |
Concepts:
The kinematic indeterminacy is given as
Dk = 3j-r-m
j = no of joints
r = no of support reactions
m = no of axially rigid members
The kinematic indeterminacy is given as
Dk = 3j-r-m
j = no of joints
r = no of support reactions
m = no of axially rigid members
Calculation:
No of Joints, j = 3
No of support reactions, r = 5 (3 at support A, 1 at each support B and C)
No of axially rigid members, m = 0 (assumed as not given in Question )
Dk = 3j-r-m
Dk = 3 × 3 – 5 – 0
∴ Dk = 4
No of Joints, j = 3
No of support reactions, r = 5 (3 at support A, 1 at each support B and C)
No of axially rigid members, m = 0 (assumed as not given in Question )
Dk = 3j-r-m
Dk = 3 × 3 – 5 – 0
∴ Dk = 4
The following methods are used for structural analysis:
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sectionsThose used for indeterminate structural analysis would include- a)1 and 2
- b)1 and 3
- c)2 and 3
- d)2, 3 and 4
Correct answer is option 'C'. Can you explain this answer?
The following methods are used for structural analysis:
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sections
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sections
Those used for indeterminate structural analysis would include
a)
1 and 2
b)
1 and 3
c)
2 and 3
d)
2, 3 and 4

|
Rounak Mehta answered |
Macaulay's method is used for deflection and slope calculation due to point loads in prismatic beams. Method of sections is used for statically determinate trusses.
Hinged supports offers vertical and ________ reaction.- a)Horizontal
- b)Moment
- c)Rotation
- d)Couple
Correct answer is option 'A'. Can you explain this answer?
Hinged supports offers vertical and ________ reaction.
a)
Horizontal
b)
Moment
c)
Rotation
d)
Couple
|
|
Sudhir Patel answered |
A hinged support offers a vertical and horizontal reaction. The pin jointed support offers resistance against horizontal and vertical movements but not against rotation movement.
A horizontal fixed beam AB of span 6 m has uniform flexural rigidity of 4200 kN m2. During loading, the support B sinks downwards by 25 mm. The moment induced at the end A is- a)105 kN m (Anticlockwise)
- b)17.5 kN m (Clockwise)
- c)17.5 kN m (Anticlockwise)
- d)105 kN m (Clockwise)
Correct answer is option 'C'. Can you explain this answer?
A horizontal fixed beam AB of span 6 m has uniform flexural rigidity of 4200 kN m2. During loading, the support B sinks downwards by 25 mm. The moment induced at the end A is
a)
105 kN m (Anticlockwise)
b)
17.5 kN m (Clockwise)
c)
17.5 kN m (Anticlockwise)
d)
105 kN m (Clockwise)

|
Mehul Choudhury answered |
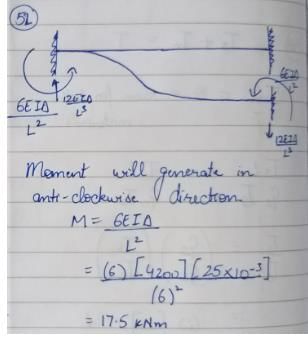
The kinematic indeterminacy of the following beam after imposing the boundary
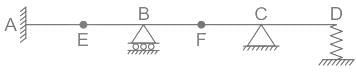
- a)6
- b)8
- c)10
- d)12
Correct answer is option 'C'. Can you explain this answer?
The kinematic indeterminacy of the following beam after imposing the boundary


a)
6
b)
8
c)
10
d)
12

|
Pioneer Academy answered |
Kinematic Indeterminacy (DK):
- Also known as the degree of freedom (DOF)
- It refers to the number of independent components of joint displacement with the specified set of axes.
- If the plane frame is extensible, the degree of kinematic indeterminacy = (3j - r)
- If plane frame is inextensible & unbraced, Degree of kinematic indeterminacy = 3j - (r + m)
- Here j = no. of Joints, r = No. of Unknown Equations, m = no. of Plastic hinges equation (m'-1), m' = No. of member meeting at hinges
Calculation:
As per the above diagram:
No. of joints (j) = 7
No. of unknown Equation (r) = 3(Fixed end) +1 (Roller Support ) +2 (Hinged Support ) +1 (Spring as prop) = 7
No. of member meeting at hinges = 5
m = 5 - 1 = 4
Putting in formula Dk = 3j - (r + m)
Dk = 3 × 7 - (7 + 4)
Dk = 21 - 11
Dk = 10
So the Dk of the following beam is 10.
As per the above diagram:
No. of joints (j) = 7
No. of unknown Equation (r) = 3(Fixed end) +1 (Roller Support ) +2 (Hinged Support ) +1 (Spring as prop) = 7
No. of member meeting at hinges = 5
m = 5 - 1 = 4
Putting in formula Dk = 3j - (r + m)
Dk = 3 × 7 - (7 + 4)
Dk = 21 - 11
Dk = 10
So the Dk of the following beam is 10.
For the plane frame as shown in the figure
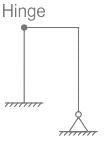
The degree of kinematic indeterminacy, neglecting axial deformation, is- a)3
- b)5
- c)7
- d)9
Correct answer is option 'B'. Can you explain this answer?
For the plane frame as shown in the figure

The degree of kinematic indeterminacy, neglecting axial deformation, is

The degree of kinematic indeterminacy, neglecting axial deformation, is
a)
3
b)
5
c)
7
d)
9

|
Pioneer Academy answered |
Concept:
Static Indeterminacy: If the equilibrium equations are enough to analyze for unknown reactions, the structure is said to be statically indeterminate.
Ds = Dse + Dsi
Dse = r – S
Dsi = 3 × Number of closed loop (For portal frame)
Dsi = m- 2j+ 3 (For truss structure)
Kinematic Indeterminacy: It is the total number of possible degree of freedom of all the joints.
Dk = 3J - r (For beam & portal frame)
Dk = 2J - r (For truss structure)
where, Dse = External Indeterminacy, Dsi = Internal Indeterminacy, Dk = Kinematic Indeterminacy, r = No. of unknown reactions, S = No. of equilibrium equation, m = No. of mombers & J = No. of joints
Dk = 3J - r + H = 3 × 4 – 5 + 1 = 8
Dk = 8 - 3 = 5
Static Indeterminacy: If the equilibrium equations are enough to analyze for unknown reactions, the structure is said to be statically indeterminate.
Ds = Dse + Dsi
Dse = r – S
Dsi = 3 × Number of closed loop (For portal frame)
Dsi = m- 2j+ 3 (For truss structure)
Kinematic Indeterminacy: It is the total number of possible degree of freedom of all the joints.
Dk = 3J - r (For beam & portal frame)
Dk = 2J - r (For truss structure)
where, Dse = External Indeterminacy, Dsi = Internal Indeterminacy, Dk = Kinematic Indeterminacy, r = No. of unknown reactions, S = No. of equilibrium equation, m = No. of mombers & J = No. of joints
Dk = 3J - r + H = 3 × 4 – 5 + 1 = 8
Dk = 8 - 3 = 5
Find the reaction at simple support A?
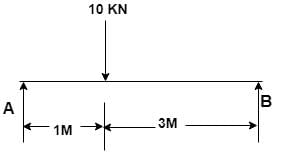
- a)6.5 kN
- b)9 kN
- c)10 kN
- d)7.5 kN
Correct answer is option 'D'. Can you explain this answer?
Find the reaction at simple support A?


a)
6.5 kN
b)
9 kN
c)
10 kN
d)
7.5 kN

|
Vertex Academy answered |
Total load = 10 kN
Taking moment at A = 0
4 × R @ B – 10 = 0
R @ B = 2.5 kN
Reaction at A = 10 – 2.5 = 7.5kN.
Taking moment at A = 0
4 × R @ B – 10 = 0
R @ B = 2.5 kN
Reaction at A = 10 – 2.5 = 7.5kN.
If 4 reactions are acting on a beam, then the system is:-- a)Unstable & indeterminate
- b)Can’t say
- c)Stable & indeterminate
- d)Stable & determinate
Correct answer is option 'B'. Can you explain this answer?
If 4 reactions are acting on a beam, then the system is:-
a)
Unstable & indeterminate
b)
Can’t say
c)
Stable & indeterminate
d)
Stable & determinate
|
|
Kabir Verma answered |
4 reactions mean that the system is definitely indeterminate. But stability would depend upon the nature of forces acting on the planar structure.
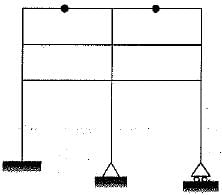
The total degree of kinematic indeterminacy of the plane frame shown in the given figure considering columns to be axially rigid is
- a)20
- b)37
- c)44
- d)28
Correct answer is option 'D'. Can you explain this answer?
The total degree of kinematic indeterminacy of the plane frame shown in the given figure considering columns to be axially rigid is


a)
20
b)
37
c)
44
d)
28

|
Moumita Rane answered |
Dk = [3(j + j) - re] + rr - m
where,
j = total number of rigid joints = 12
j' = total number of hybrid joints = 2
re = total number of external reactions
= 3+ 2 + 2 = 7
rr =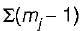 = (2 - 1) + (2 - 1) = 2
= (2 - 1) + (2 - 1) = 2
m = total number of axially rigid member = 9
∴ Dk = [3(12 + 2) - 7] + 2 - 9 = 35 - 7 = 28
where,
j = total number of rigid joints = 12
j' = total number of hybrid joints = 2
re = total number of external reactions
= 3+ 2 + 2 = 7
rr =
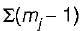 = (2 - 1) + (2 - 1) = 2
= (2 - 1) + (2 - 1) = 2m = total number of axially rigid member = 9
∴ Dk = [3(12 + 2) - 7] + 2 - 9 = 35 - 7 = 28
The kinematics indeterminacy of the beam as shown in figure is

- a)5
- b)9
- c)14
- d)15
Correct answer is option 'B'. Can you explain this answer?
The kinematics indeterminacy of the beam as shown in figure is


a)
5
b)
9
c)
14
d)
15

|
Sravya Tiwari answered |
The kinematic indeterminacy of the beam is given by,
Dk = 3j - re + rr
Now, j = 5
re = 7
rr = 1
∴ Dk = 3 x 5 - 7 + 1 = 9
Dk = 3j - re + rr
Now, j = 5
re = 7
rr = 1
∴ Dk = 3 x 5 - 7 + 1 = 9
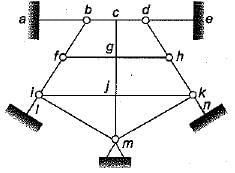
The degree of static indeterminacy of the hybrid plane frame as shown in figure is
- a)10
- b)11
- c)12
- d)13
Correct answer is option 'D'. Can you explain this answer?
The degree of static indeterminacy of the hybrid plane frame as shown in figure is


a)
10
b)
11
c)
12
d)
13

|
Pallabi Kulkarni answered |
Ds = Dse + Dsi
Dse = re - 3 = 14 - 3 = 11
Dsi = 3c - rr
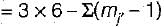
= 18 - ( 2 + 2 + 3 + 2 + 3 + 2 + 2)
= 18 - (16) = 2
∴ Ds = 11 + 2 = 13
Dse = re - 3 = 14 - 3 = 11
Dsi = 3c - rr
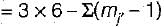
= 18 - ( 2 + 2 + 3 + 2 + 3 + 2 + 2)
= 18 - (16) = 2
∴ Ds = 11 + 2 = 13
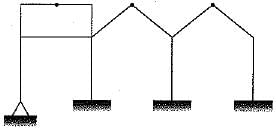
The statical indeterminacy for the given 2D frame is
- a)8
- b)6
- c)9
- d)11
Correct answer is option 'D'. Can you explain this answer?
The statical indeterminacy for the given 2D frame is


a)
8
b)
6
c)
9
d)
11

|
Samridhi Choudhary answered |
Ds = Dse + Dsi
Dse = rE - 3
rE = 2 + 3 + 3 + 3 = 11
Dse = 8
Dsi = 3C - rR
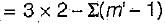
= 6 - (2 - 1) + (2 - 1) + (2 - 1) = 3
∴ Ds = 8 + 3 = 11
Dse = rE - 3
rE = 2 + 3 + 3 + 3 = 11
Dse = 8
Dsi = 3C - rR
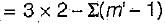
= 6 - (2 - 1) + (2 - 1) + (2 - 1) = 3
∴ Ds = 8 + 3 = 11
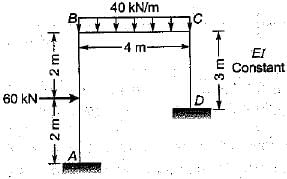
The figure given above shows a rigid frame. If D . is lateral translation of the joints, slope deflection equation for the member BA be written as:
- a)
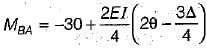
- b)
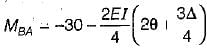
- c)
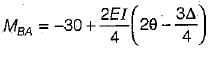
- d)
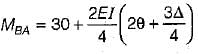
Correct answer is option 'B'. Can you explain this answer?
The figure given above shows a rigid frame. If D . is lateral translation of the joints, slope deflection equation for the member BA be written as:


a)
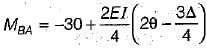
b)
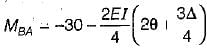
c)
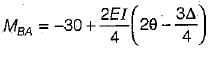
d)
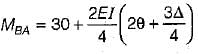

|
Ameya Sen answered |
Taking;
- anticlockwise end moment positive
- anticlockwise rotation at member end positive
- anticlockwise chord rotation positive
FEMba = 30 kN-m
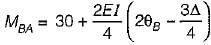
- anticlockwise end moment positive
- anticlockwise rotation at member end positive
- anticlockwise chord rotation positive
FEMba = 30 kN-m
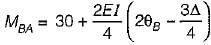
What is kinematic indeterminacy for the given figure without considering axial deformation?

- a)0
- b)2
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
What is kinematic indeterminacy for the given figure without considering axial deformation?


a)
0
b)
2
c)
4
d)
6
|
|
Anjana Singh answered |
The given beam is supported by roller support at both of its ends. Roller support, if not considering axial deformation has one degree of freedom i.e. Rotation. Therefore, the degree of freedom of the beam is 2.
What is kinematic indeterminacy for the given figure without considering axial deformation?
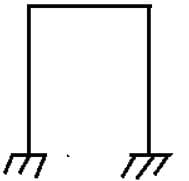
- a)0
- b)2
- c)3
- d)6
Correct answer is option 'C'. Can you explain this answer?
What is kinematic indeterminacy for the given figure without considering axial deformation?


a)
0
b)
2
c)
3
d)
6
|
|
Sudhir Patel answered |
The given set of frame consists of fixed end supports with two intermediate rigid joints. Each rigid joint allows horizontal sway, vertical sway, and rotation. But since the axial deformation is to be neglected. Therefore, vertical sway of the joints and either horizontal sway of a joint is neglected. Hence, degree of freedom is three.
A portal frame is shown in the given figure. If θB - θc = 400/EI radian, then the value of moment at B will be
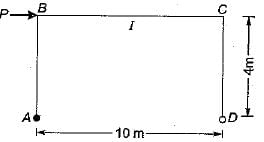
- a)120 kNm
- b)240 kNm
- c)360 kNm
- d)480 kNm
Correct answer is option 'B'. Can you explain this answer?
A portal frame is shown in the given figure. If θB - θc = 400/EI radian, then the value of moment at B will be


a)
120 kNm
b)
240 kNm
c)
360 kNm
d)
480 kNm

|
Sakshi Basak answered |
The deformed shape of structure will have translation at B and C,
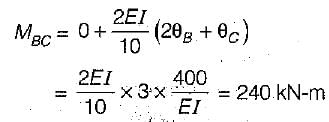
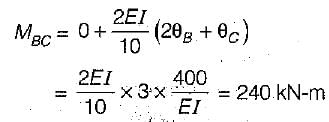
What is the degree of static indeterminacy of the plane structure as shown in the figure below?
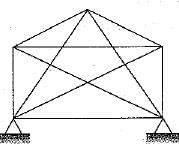
- a)3
- b)4
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
What is the degree of static indeterminacy of the plane structure as shown in the figure below?


a)
3
b)
4
c)
5
d)
6

|
Raghav Mukherjee answered |
For plane truss degree of indeterminacy,
Ds = m + re - 2j
re = 4; m= 10; j = 5
Ds = 4 + 10 - 2 x 5 = 4
Ds = m + re - 2j
re = 4; m= 10; j = 5
Ds = 4 + 10 - 2 x 5 = 4
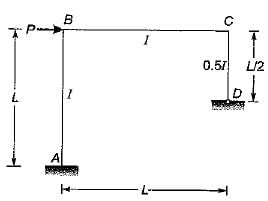
The given figure shows a portal frame with one end fixed and other hinged. The ratio of the fixed end moments MBA/MCD due to side sway will be
- a)1.0
- b)2.0
- c)2.5
- d)3.0
Correct answer is option 'A'. Can you explain this answer?
The given figure shows a portal frame with one end fixed and other hinged. The ratio of the fixed end moments MBA/MCD due to side sway will be


a)
1.0
b)
2.0
c)
2.5
d)
3.0

|
Harshad Iyer answered |
Due to sway, the deflection of point B will be equal to that of point C.
How is a truss, which undergoes rigid body translation for an arbitrary load, classified as?- a)Determinate structure
- b)Geometrically unstable structure
- c)Statically unstable structure
- d)Structurally unstable structure
Correct answer is option 'B'. Can you explain this answer?
How is a truss, which undergoes rigid body translation for an arbitrary load, classified as?
a)
Determinate structure
b)
Geometrically unstable structure
c)
Statically unstable structure
d)
Structurally unstable structure
|
|
Maheshwar Das answered |
Geometrically unstable structure
A truss is a structural framework composed of straight members connected at joints. It is used to support loads and distribute them evenly throughout the structure. Trusses are commonly used in bridges, roofs, and other load-bearing structures.
Classification of trusses
Trusses can be classified into several categories based on their characteristics. One classification is based on the behavior of the truss under external loads. Trusses can be categorized as determinate or indeterminate structures.
Determinate structures
Determinate structures are those in which the reactions and internal forces can be determined solely using the equations of static equilibrium. These structures have a unique solution for all the unknowns. In other words, the reactions and forces in each member can be determined by solving a set of simultaneous equations.
Statically unstable structures
Statically unstable structures are those that cannot be analyzed using the equations of static equilibrium alone. These structures have more unknowns than the number of equations available, making it impossible to determine the reactions and internal forces without additional information or assumptions.
Structurally unstable structures
Structurally unstable structures are those that fail to maintain their shape or stability when subjected to external loads. They are unable to resist the applied loads and may collapse or deform significantly. These structures generally have insufficient stiffness or strength to support the applied loads.
Geometrically unstable structures
Geometrically unstable structures are those that undergo rigid body translation under an arbitrary load. Rigid body translation refers to the movement of the entire structure as a whole, without any deformation or change in shape of individual members. In such structures, the joints are not rigid enough to maintain the shape of the truss, causing it to move as a unit.
Explanation of the correct answer
Based on the given options, the correct answer is option 'B' - Geometrically unstable structure. This is because a truss that undergoes rigid body translation for an arbitrary load does not maintain its shape and exhibits movement as a whole. The joints in the truss are not rigid enough to resist the translation, resulting in a geometrically unstable structure.
A truss is a structural framework composed of straight members connected at joints. It is used to support loads and distribute them evenly throughout the structure. Trusses are commonly used in bridges, roofs, and other load-bearing structures.
Classification of trusses
Trusses can be classified into several categories based on their characteristics. One classification is based on the behavior of the truss under external loads. Trusses can be categorized as determinate or indeterminate structures.
Determinate structures
Determinate structures are those in which the reactions and internal forces can be determined solely using the equations of static equilibrium. These structures have a unique solution for all the unknowns. In other words, the reactions and forces in each member can be determined by solving a set of simultaneous equations.
Statically unstable structures
Statically unstable structures are those that cannot be analyzed using the equations of static equilibrium alone. These structures have more unknowns than the number of equations available, making it impossible to determine the reactions and internal forces without additional information or assumptions.
Structurally unstable structures
Structurally unstable structures are those that fail to maintain their shape or stability when subjected to external loads. They are unable to resist the applied loads and may collapse or deform significantly. These structures generally have insufficient stiffness or strength to support the applied loads.
Geometrically unstable structures
Geometrically unstable structures are those that undergo rigid body translation under an arbitrary load. Rigid body translation refers to the movement of the entire structure as a whole, without any deformation or change in shape of individual members. In such structures, the joints are not rigid enough to maintain the shape of the truss, causing it to move as a unit.
Explanation of the correct answer
Based on the given options, the correct answer is option 'B' - Geometrically unstable structure. This is because a truss that undergoes rigid body translation for an arbitrary load does not maintain its shape and exhibits movement as a whole. The joints in the truss are not rigid enough to resist the translation, resulting in a geometrically unstable structure.
Chapter doubts & questions for Determinacy & Indeterminacy of Structures - Structural Analysis 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Determinacy & Indeterminacy of Structures - Structural Analysis in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Structural Analysis
34 videos|164 docs|31 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup