JEE Exam > JEE Questions > The combined equation to two parabolas, both ...
Start Learning for Free
The combined equation to two parabolas, both have their axis along x-axis, is given by y4 - y2 (4x + 4 - 2 sin22α) + sin22α (4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°
is
is
- a)another parabola
- b)circle
- c)a line midway between the tangents at vertices
- d)a line midway between their directrices
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The combined equation to two parabolas, both have their axis along x-a...
The parabolas are y2 = 4sin2 α(x + sin2α) and y2 = 4cos2 α(x + cos2α), hence the locus is x + cos2α + sin2α = 0 ⇒ x + 1 = 0
Assume the point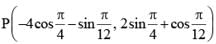
as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
Similarly A3(-2, 0), A4 (0, -2√2) etc.
Assume the point
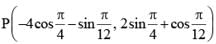as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)Similarly A3(-2, 0), A4 (0, -2√2) etc.
Most Upvoted Answer
The combined equation to two parabolas, both have their axis along x-a...
Understanding the Problem
The problem deals with the intersection of tangents to two parabolas that open along the x-axis. The given equation represents a combined form of these parabolas, and we need to analyze the conditions under which the tangents intersect at a right angle.
Key Concepts
- Parabolas Orientation: Both parabolas are oriented along the x-axis, meaning their equations can be expressed in a standard form with respect to y.
- Tangents to Parabolas: The tangents to a parabola can be determined using the properties of quadratic equations.
- Intersection of Tangents: When two tangents intersect at a right angle, their slopes must be negative reciprocals of each other.
Angle Between Tangents
When tangents are drawn to both parabolas and they enclose an angle of 90 degrees, the locus of the point where they intersect can be derived from the properties of the parabolas.
Locus of Intersection
- The locus of the intersection points of tangents drawn to the parabolas will lead to a specific geometric figure.
- For parabolas, it is established that if tangents intersect at right angles, the locus is not another parabola or a circle, but rather a line.
Correct Answer Explanation
The correct answer is option 'D': a line midway between their directrices. This conclusion is based on:
- Directrices of Parabolas: The directrix of a parabola is a fixed line used in its definition.
- Midway Line: The line that is midway between the directrices will serve as the locus for the intersection of tangents that are at right angles to each other.
In summary, the analysis of the tangents and their intersection leads to a linear locus, specifically a line that is equidistant from the directrices of the two parabolas. This aligns with the properties of geometric configurations involving parabolas.
The problem deals with the intersection of tangents to two parabolas that open along the x-axis. The given equation represents a combined form of these parabolas, and we need to analyze the conditions under which the tangents intersect at a right angle.
Key Concepts
- Parabolas Orientation: Both parabolas are oriented along the x-axis, meaning their equations can be expressed in a standard form with respect to y.
- Tangents to Parabolas: The tangents to a parabola can be determined using the properties of quadratic equations.
- Intersection of Tangents: When two tangents intersect at a right angle, their slopes must be negative reciprocals of each other.
Angle Between Tangents
When tangents are drawn to both parabolas and they enclose an angle of 90 degrees, the locus of the point where they intersect can be derived from the properties of the parabolas.
Locus of Intersection
- The locus of the intersection points of tangents drawn to the parabolas will lead to a specific geometric figure.
- For parabolas, it is established that if tangents intersect at right angles, the locus is not another parabola or a circle, but rather a line.
Correct Answer Explanation
The correct answer is option 'D': a line midway between their directrices. This conclusion is based on:
- Directrices of Parabolas: The directrix of a parabola is a fixed line used in its definition.
- Midway Line: The line that is midway between the directrices will serve as the locus for the intersection of tangents that are at right angles to each other.
In summary, the analysis of the tangents and their intersection leads to a linear locus, specifically a line that is equidistant from the directrices of the two parabolas. This aligns with the properties of geometric configurations involving parabolas.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.
|
Explore Courses for JEE exam
|
|
Similar JEE Doubts
Top Courses for JEEView all
The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer?
Question Description
The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer?.
The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The combined equation to two parabolas, both have their axis along x-axis, is given byy4 - y2(4x + 4 - 2 sin22α) + sin22α(4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°isa)another parabolab)circlec)a line midway between the tangents at verticesd)a line midway between their directricesCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup