Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The ratio of crippling loads of a column havi...
Start Learning for Free
The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, is
- a)4
- b)2
- c)1
- d)3
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
The ratio of crippling loads of a column having both the ends fixed to...
Crippling load is given by:
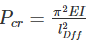
For both ends fixed, 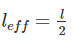
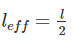
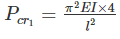
For both ends hinged, leff = l
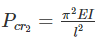
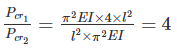
Most Upvoted Answer
The ratio of crippling loads of a column having both the ends fixed to...
Ratio of Crippling Loads of a Column with Fixed Ends to Hinged Ends
Introduction:
In structural engineering, the crippling load refers to the maximum load that a column can sustain before it undergoes buckling or failure. The behavior of a column under load depends on its end conditions, which can be either fixed or hinged. The ratio of crippling loads for columns with fixed ends to those with hinged ends can be determined using theoretical analysis.
Explanation:
To understand the ratio of crippling loads for columns with different end conditions, let's consider the following points:
1. Fixed Ends:
A column with fixed ends is one that is rigidly connected to its supports. It is fully restrained against both translation and rotation at both ends. The fixed ends prevent any lateral movement or rotation of the column.
2. Hinged Ends:
A column with hinged ends is one that is free to rotate at its supports. It is restrained against translation but allows rotation at both ends. The hinged ends allow the column to rotate and deflect under load.
3. Buckling and Crippling:
When a compressive load is applied to a column, it tends to buckle or deflect laterally. Buckling occurs when the critical load is reached, causing the column to fail. Crippling refers specifically to the failure of a column under compressive load due to local buckling.
4. Euler's Buckling Formula:
Euler's buckling formula is commonly used to determine the critical load for buckling of columns. According to this formula, the critical load (P) for a column with length (L), effective length factor (K), and modulus of elasticity (E) can be calculated using the following equation:
P = (π² * E * I) / (K * L)²
Where I is the moment of inertia of the column cross-section.
5. Ratio of Crippling Loads:
To determine the ratio of crippling loads for columns with fixed ends to those with hinged ends, we can compare the critical loads calculated using Euler's buckling formula for both cases.
Let's assume the lengths of the columns with fixed ends and hinged ends are the same (L). The effective length factor (K) for a column with fixed ends is 1, while for a column with hinged ends, it is 2.
Using the formula for critical load, we can calculate the critical loads for both cases:
P_fixed = (π² * E * I) / L²
P_hinged = (π² * E * I) / (2 * L)²
By dividing the critical load for the column with fixed ends by the critical load for the column with hinged ends, we get:
P_fixed / P_hinged = (L/2)² / L² = 1/4
Therefore, the ratio of crippling loads for a column with fixed ends to a column with hinged ends is 1:4 or 1/4.
Conclusion:
The correct answer is option A, which states that the ratio of crippling loads for a column with fixed ends to a column with hinged ends is 4. This ratio is derived from Euler's buckling formula and the respective effective length factors for both end conditions.
Introduction:
In structural engineering, the crippling load refers to the maximum load that a column can sustain before it undergoes buckling or failure. The behavior of a column under load depends on its end conditions, which can be either fixed or hinged. The ratio of crippling loads for columns with fixed ends to those with hinged ends can be determined using theoretical analysis.
Explanation:
To understand the ratio of crippling loads for columns with different end conditions, let's consider the following points:
1. Fixed Ends:
A column with fixed ends is one that is rigidly connected to its supports. It is fully restrained against both translation and rotation at both ends. The fixed ends prevent any lateral movement or rotation of the column.
2. Hinged Ends:
A column with hinged ends is one that is free to rotate at its supports. It is restrained against translation but allows rotation at both ends. The hinged ends allow the column to rotate and deflect under load.
3. Buckling and Crippling:
When a compressive load is applied to a column, it tends to buckle or deflect laterally. Buckling occurs when the critical load is reached, causing the column to fail. Crippling refers specifically to the failure of a column under compressive load due to local buckling.
4. Euler's Buckling Formula:
Euler's buckling formula is commonly used to determine the critical load for buckling of columns. According to this formula, the critical load (P) for a column with length (L), effective length factor (K), and modulus of elasticity (E) can be calculated using the following equation:
P = (π² * E * I) / (K * L)²
Where I is the moment of inertia of the column cross-section.
5. Ratio of Crippling Loads:
To determine the ratio of crippling loads for columns with fixed ends to those with hinged ends, we can compare the critical loads calculated using Euler's buckling formula for both cases.
Let's assume the lengths of the columns with fixed ends and hinged ends are the same (L). The effective length factor (K) for a column with fixed ends is 1, while for a column with hinged ends, it is 2.
Using the formula for critical load, we can calculate the critical loads for both cases:
P_fixed = (π² * E * I) / L²
P_hinged = (π² * E * I) / (2 * L)²
By dividing the critical load for the column with fixed ends by the critical load for the column with hinged ends, we get:
P_fixed / P_hinged = (L/2)² / L² = 1/4
Therefore, the ratio of crippling loads for a column with fixed ends to a column with hinged ends is 1:4 or 1/4.
Conclusion:
The correct answer is option A, which states that the ratio of crippling loads for a column with fixed ends to a column with hinged ends is 4. This ratio is derived from Euler's buckling formula and the respective effective length factors for both end conditions.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer?.
The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer?.
Solutions for The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer?, a detailed solution for The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, isa)4b)2c)1d)3Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























