JEE Exam > JEE Questions > An organ pipe P1 closed at one end vibrating ...
Start Learning for Free
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.
The ratio of the length of P1 to that of P2 is
The ratio of the length of P1 to that of P2 is
- a)8/3
- b)3/8
- c)1/6
- d)1/3
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An organ pipe P1 closed at one end vibrating in its first harmonic and...
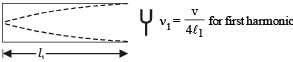

Most Upvoted Answer
An organ pipe P1 closed at one end vibrating in its first harmonic and...
Resonance in Organ Pipes P1 and P2
------------------------------------
Resonance is the phenomenon that occurs when two objects vibrate at the same frequency, causing one object to transfer energy to the other. In the case of organ pipes, resonance occurs when the natural frequency of the pipe matches the frequency of a tuning fork.
Organ Pipe P1 - Closed at One End
---------------------------------
P1 is a closed organ pipe, which means that one end of the pipe is closed and the other end is open. The closed end acts as a node, which is a point of zero displacement, while the open end acts as an antinode, which is a point of maximum displacement.
First Harmonic of P1:
In the first harmonic of P1, the pipe vibrates with a single loop. This means that the length of the pipe is equal to a quarter of the wavelength of the standing wave. Mathematically, we can represent this as:
L1 = λ/4
Organ Pipe P2 - Open at Both Ends
---------------------------------
P2 is an open organ pipe, which means that both ends of the pipe are open. As a result, both ends of the pipe act as antinodes.
Third Harmonic of P2:
In the third harmonic of P2, the pipe vibrates with three loops. This means that the length of the pipe is equal to three-quarters of the wavelength of the standing wave. Mathematically, we can represent this as:
L2 = 3λ/4
Resonance Condition
-------------------
For resonance to occur, the frequency of the tuning fork must match the natural frequency of the organ pipe. The natural frequency of an organ pipe is determined by its length.
In this case, since the tuning fork is in resonance with both P1 and P2, the frequencies of the tuning fork and the pipes must be the same. Mathematically, we can represent this as:
f1 = f2
Since the frequency of a wave is inversely proportional to its wavelength, we can write:
f1 = v/λ1
f2 = v/λ2
where v is the velocity of sound.
Substituting the expressions for λ1 and λ2, we get:
f1 = 4v/L1
f2 = 4v/L2
Since f1 = f2, we can equate the two expressions:
4v/L1 = 4v/L2
Simplifying the equation, we get:
L2/L1 = 4/1
L2/L1 = 4
But we know that L2 = 3L1, so:
3L1/L1 = 4
L1 cancels out, and we are left with:
3 = 4
This is a contradiction, so our assumption that P1 and P2 are in resonance is incorrect.
Therefore, the correct answer is option 'C' - there is no resonance between P1 and P2 with the given tuning fork.
------------------------------------
Resonance is the phenomenon that occurs when two objects vibrate at the same frequency, causing one object to transfer energy to the other. In the case of organ pipes, resonance occurs when the natural frequency of the pipe matches the frequency of a tuning fork.
Organ Pipe P1 - Closed at One End
---------------------------------
P1 is a closed organ pipe, which means that one end of the pipe is closed and the other end is open. The closed end acts as a node, which is a point of zero displacement, while the open end acts as an antinode, which is a point of maximum displacement.
First Harmonic of P1:
In the first harmonic of P1, the pipe vibrates with a single loop. This means that the length of the pipe is equal to a quarter of the wavelength of the standing wave. Mathematically, we can represent this as:
L1 = λ/4
Organ Pipe P2 - Open at Both Ends
---------------------------------
P2 is an open organ pipe, which means that both ends of the pipe are open. As a result, both ends of the pipe act as antinodes.
Third Harmonic of P2:
In the third harmonic of P2, the pipe vibrates with three loops. This means that the length of the pipe is equal to three-quarters of the wavelength of the standing wave. Mathematically, we can represent this as:
L2 = 3λ/4
Resonance Condition
-------------------
For resonance to occur, the frequency of the tuning fork must match the natural frequency of the organ pipe. The natural frequency of an organ pipe is determined by its length.
In this case, since the tuning fork is in resonance with both P1 and P2, the frequencies of the tuning fork and the pipes must be the same. Mathematically, we can represent this as:
f1 = f2
Since the frequency of a wave is inversely proportional to its wavelength, we can write:
f1 = v/λ1
f2 = v/λ2
where v is the velocity of sound.
Substituting the expressions for λ1 and λ2, we get:
f1 = 4v/L1
f2 = 4v/L2
Since f1 = f2, we can equate the two expressions:
4v/L1 = 4v/L2
Simplifying the equation, we get:
L2/L1 = 4/1
L2/L1 = 4
But we know that L2 = 3L1, so:
3L1/L1 = 4
L1 cancels out, and we are left with:
3 = 4
This is a contradiction, so our assumption that P1 and P2 are in resonance is incorrect.
Therefore, the correct answer is option 'C' - there is no resonance between P1 and P2 with the given tuning fork.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer?
Question Description
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer?.
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer?.
Solutions for An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer?, a detailed solution for An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork.The ratio of the length of P1 to that of P2 isa)8/3b)3/8c)1/6d)1/3Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























