Class 11 Exam > Class 11 Questions > A heavy block of mass M is slowly placed on a...
Start Learning for Free
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v. The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?
- a)v/ug
- b)v2/ug
- c)v/2ug
- d)v2/2ug
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A heavy block of mass M is slowly placed on a conveyor belt moving wit...
Frictional force on the block = μMg
It will be causing acceleration a =μMg/M = μg
The block slide on the ball till its velocity becomes ‘v’ given by the equation
Most Upvoted Answer
A heavy block of mass M is slowly placed on a conveyor belt moving wit...
To solve this problem, we can use the concept of friction and Newton's second law of motion.
1. Understanding the problem:
A heavy block of mass M is placed on a conveyor belt moving with a speed v. The coefficient of friction between the block and the belt is μ. We need to find the distance the block will slide on the belt before coming to rest.
2. Analyzing the forces acting on the block:
- The weight of the block acts vertically downwards with a force of mg (where g is the acceleration due to gravity).
- The normal force acts perpendicular to the surface of the belt and is equal to the weight of the block, which is mg.
- The frictional force acts horizontally opposite to the direction of motion and is given by f = μN.
3. Applying Newton's second law of motion:
The net force acting on the block is the difference between the applied force (friction) and the opposing force (weight). Therefore, we can write:
ma = f - mg
4. Solving for acceleration:
Substituting the values of f and N, we get:
ma = μmg - mg
a = μg - g
a = g(μ - 1)
5. Calculating the time taken to stop:
The block will come to rest when its final velocity becomes zero. Using the equation of motion v = u + at, where u is the initial velocity (which is the speed of the conveyor belt), we can write:
0 = v + a(t)
t = -v/a
t = -v/(g(μ - 1))
6. Calculating the distance traveled:
The distance traveled by the block can be calculated using the equation of motion s = ut + (1/2)at^2. Since the initial velocity u is equal to v, we have:
s = vt + (1/2)at^2
s = v(-v/(g(μ - 1))) + (1/2)(g(μ - 1))^2(-v/(g(μ - 1)))^2
s = -v^2/(g(μ - 1)) - v^2/(2g(μ - 1))
s = -2v^2/(2g(μ - 1)) - v^2/(2g(μ - 1))
s = -3v^2/(2g(μ - 1))
s = v^2/(2g(1 - μ))
7. Simplifying the expression:
Since the coefficient of friction (μ) is less than 1, the denominator (1 - μ) will be positive. Therefore, we can simplify the expression as follows:
s = v^2/(2g(1 - μ))
s = v^2/(2g - 2gμ)
s = v^2/(2g(1 - μ))
s = v^2/2gμ
8. Comparing the answer choices:
The correct answer is option 'D', which matches the derived expression for the distance traveled by the block: v^2/(2gμ).
1. Understanding the problem:
A heavy block of mass M is placed on a conveyor belt moving with a speed v. The coefficient of friction between the block and the belt is μ. We need to find the distance the block will slide on the belt before coming to rest.
2. Analyzing the forces acting on the block:
- The weight of the block acts vertically downwards with a force of mg (where g is the acceleration due to gravity).
- The normal force acts perpendicular to the surface of the belt and is equal to the weight of the block, which is mg.
- The frictional force acts horizontally opposite to the direction of motion and is given by f = μN.
3. Applying Newton's second law of motion:
The net force acting on the block is the difference between the applied force (friction) and the opposing force (weight). Therefore, we can write:
ma = f - mg
4. Solving for acceleration:
Substituting the values of f and N, we get:
ma = μmg - mg
a = μg - g
a = g(μ - 1)
5. Calculating the time taken to stop:
The block will come to rest when its final velocity becomes zero. Using the equation of motion v = u + at, where u is the initial velocity (which is the speed of the conveyor belt), we can write:
0 = v + a(t)
t = -v/a
t = -v/(g(μ - 1))
6. Calculating the distance traveled:
The distance traveled by the block can be calculated using the equation of motion s = ut + (1/2)at^2. Since the initial velocity u is equal to v, we have:
s = vt + (1/2)at^2
s = v(-v/(g(μ - 1))) + (1/2)(g(μ - 1))^2(-v/(g(μ - 1)))^2
s = -v^2/(g(μ - 1)) - v^2/(2g(μ - 1))
s = -2v^2/(2g(μ - 1)) - v^2/(2g(μ - 1))
s = -3v^2/(2g(μ - 1))
s = v^2/(2g(1 - μ))
7. Simplifying the expression:
Since the coefficient of friction (μ) is less than 1, the denominator (1 - μ) will be positive. Therefore, we can simplify the expression as follows:
s = v^2/(2g(1 - μ))
s = v^2/(2g - 2gμ)
s = v^2/(2g(1 - μ))
s = v^2/2gμ
8. Comparing the answer choices:
The correct answer is option 'D', which matches the derived expression for the distance traveled by the block: v^2/(2gμ).
Free Test
FREE
| Start Free Test |
Community Answer
A heavy block of mass M is slowly placed on a conveyor belt moving wit...
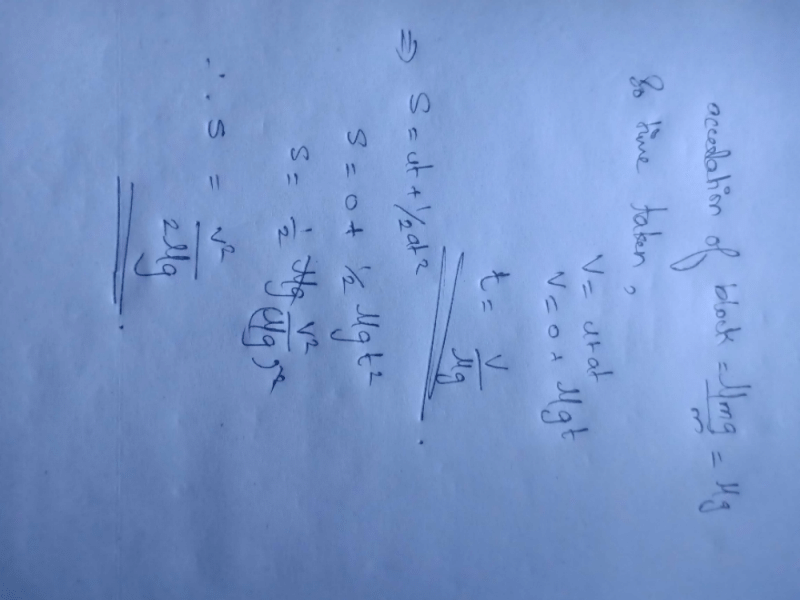

|
Explore Courses for Class 11 exam
|

|
Question Description
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer?.
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v.The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?a)v/ugb)v2/ugc)v/2ugd)v2/2ugCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















