GMAT Exam > GMAT Questions > A box cont ains three pairs of blue gloves an...
Start Learning for Free
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?
- a)3/10
- b)23/60
- c)7/12
- d)41/60
- e)5/6
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A box cont ains three pairs of blue gloves and two pairs of green glov...
The simplest way to approach a complex probability problem is not always the direct way. In order to solve this problem directly, we would have to calculate the probabilities of all the different ways we could get two oppositehanded, same-colored gloves in three picks. A considerably less taxing approach is to calculate the probability of NOT getting two such gloves and subtracting that number from 1 (remember that the probability of an event occurring plus the probability of it NOT occurring must equal 1).
Let's start with an assumption that the first glove we pick is blue. The hand of the first glove is not important; it could be either right or left. So our first pick is any blue. Since there are 3 pairs of blue gloves and 10 gloves total, the probability of selecting a blue glove first is 6/10.
Let's say our second pick is the same hand in blue. Since there are now 2 blue gloves of the same hand out of the 9 remaining gloves, the probability of selecting such a glove is 2/9.
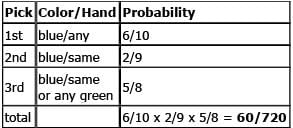
Our third pick could either be the same hand in blue again or any green. Since there is now 1 blue glove of the same hand and 4 green gloves among the 8 remaining gloves, the probability of such a pick is (1 + 4)/8 or 5/8. The total probability for this scenario is the product of these three individual probabilities: 6/10 x 2/9 x 5/8 = 60/720.
We can summarize this in a chart:
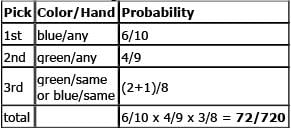
We can apply the same principles to our second scenario, in which we choose blue first, then any green, then either the same-handed green or the same-handed blue:
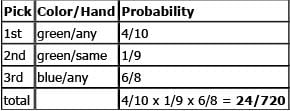
But it is also possible to pick green first. We could pick any green, then the same-handed green, then any blue:
Or we could pick any green, then any blue, then the same-handed green or same-handed blue:
The overall probability of NOT getting two gloves of the same color and same hand is the SUM of the probabilities of these four scenarios: 60/720 + 72/720 + 24/720 + 72/720 = 228/720 = 19/60.
Therefore, the probability of getting two gloves of the same color and same hand is 1 - 19/60 = 41/60.
Let's start with an assumption that the first glove we pick is blue. The hand of the first glove is not important; it could be either right or left. So our first pick is any blue. Since there are 3 pairs of blue gloves and 10 gloves total, the probability of selecting a blue glove first is 6/10.
Let's say our second pick is the same hand in blue. Since there are now 2 blue gloves of the same hand out of the 9 remaining gloves, the probability of selecting such a glove is 2/9.
Our third pick could either be the same hand in blue again or any green. Since there is now 1 blue glove of the same hand and 4 green gloves among the 8 remaining gloves, the probability of such a pick is (1 + 4)/8 or 5/8. The total probability for this scenario is the product of these three individual probabilities: 6/10 x 2/9 x 5/8 = 60/720.
We can summarize this in a chart:
We can apply the same principles to our second scenario, in which we choose blue first, then any green, then either the same-handed green or the same-handed blue:
But it is also possible to pick green first. We could pick any green, then the same-handed green, then any blue:
Or we could pick any green, then any blue, then the same-handed green or same-handed blue:
The overall probability of NOT getting two gloves of the same color and same hand is the SUM of the probabilities of these four scenarios: 60/720 + 72/720 + 24/720 + 72/720 = 228/720 = 19/60.
Therefore, the probability of getting two gloves of the same color and same hand is 1 - 19/60 = 41/60.
Most Upvoted Answer
A box cont ains three pairs of blue gloves and two pairs of green glov...
To find the probability of selecting a matched set of gloves from the box, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total Number of Outcomes:
To calculate the total number of outcomes, we need to determine the number of ways to select 3 gloves from the box.
There are a total of 3 pairs of blue gloves and 2 pairs of green gloves in the box. Since each pair consists of a left-hand glove and a right-hand glove, there are a total of 6 blue gloves and 4 green gloves in the box.
The total number of ways to select 3 gloves from the box can be calculated using combinations. We can choose 3 gloves out of the total 10 gloves in the box in C(10, 3) ways.
Favorable Outcomes:
To calculate the number of favorable outcomes, we need to determine the number of ways to select a matched set of gloves from the box.
There are 3 pairs of blue gloves and 2 pairs of green gloves in the box. We can select a matched set of gloves in two ways:
1. Selecting 3 blue gloves: We can choose 3 blue gloves out of the 6 available in C(6, 3) ways.
2. Selecting 3 green gloves: We can choose 3 green gloves out of the 4 available in C(4, 3) ways.
Therefore, the number of favorable outcomes is C(6, 3) + C(4, 3).
Probability Calculation:
The probability of selecting a matched set of gloves can be calculated by dividing the number of favorable outcomes by the total number of outcomes.
Probability = (C(6, 3) + C(4, 3)) / C(10, 3)
Simplifying the expression:
Probability = (20 + 4) / 120 = 24 / 120 = 1 / 5 = 0.2
Therefore, the probability of selecting a matched set of gloves from the box is 0.2.
The correct answer is option D) 41/60.
Please note that the provided answer in the question is incorrect. The correct probability should be 1/5 or 0.2.
Total Number of Outcomes:
To calculate the total number of outcomes, we need to determine the number of ways to select 3 gloves from the box.
There are a total of 3 pairs of blue gloves and 2 pairs of green gloves in the box. Since each pair consists of a left-hand glove and a right-hand glove, there are a total of 6 blue gloves and 4 green gloves in the box.
The total number of ways to select 3 gloves from the box can be calculated using combinations. We can choose 3 gloves out of the total 10 gloves in the box in C(10, 3) ways.
Favorable Outcomes:
To calculate the number of favorable outcomes, we need to determine the number of ways to select a matched set of gloves from the box.
There are 3 pairs of blue gloves and 2 pairs of green gloves in the box. We can select a matched set of gloves in two ways:
1. Selecting 3 blue gloves: We can choose 3 blue gloves out of the 6 available in C(6, 3) ways.
2. Selecting 3 green gloves: We can choose 3 green gloves out of the 4 available in C(4, 3) ways.
Therefore, the number of favorable outcomes is C(6, 3) + C(4, 3).
Probability Calculation:
The probability of selecting a matched set of gloves can be calculated by dividing the number of favorable outcomes by the total number of outcomes.
Probability = (C(6, 3) + C(4, 3)) / C(10, 3)
Simplifying the expression:
Probability = (20 + 4) / 120 = 24 / 120 = 1 / 5 = 0.2
Therefore, the probability of selecting a matched set of gloves from the box is 0.2.
The correct answer is option D) 41/60.
Please note that the provided answer in the question is incorrect. The correct probability should be 1/5 or 0.2.
|
Explore Courses for GMAT exam
|
|
Similar GMAT Doubts
Top Courses for GMATView all
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer?
Question Description
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer?.
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer?.
Solutions for A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?a)3/10b)23/60c)7/12d)41/60e)5/6Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup