GMAT Exam > GMAT Questions > When the integer x is divided by the integer ...
Start Learning for Free
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possible
value of the quotient x/y?
I. 15.15
II. 18.16
III. 17.17
value of the quotient x/y?
I. 15.15
II. 18.16
III. 17.17
- a)I only
- b)II only
- c)III only
- d)I and II only
- e)I and III only
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
When the integer x is divided by the integer y, the remainder is 60. W...
If the integer x divided by y has a remainder of 60, then x can be expressed as:
x = ky + 60, where k is an integer (i.e. y goes into x k times with a remainder of 60)
x = ky + 60, where k is an integer (i.e. y goes into x k times with a remainder of 60)
We could also write an expression for the quotient x/y:
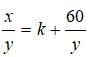
Notice that k is still the number of times that y goes into x evenly. 60/y is the decimal portion of the quotient, i.e. the remainder over the divisor y.
The first step to solving this problem is realizing that k, the number of times that y goes into x evenly, can be anything for this question since we are only given a value for the remainder. The integer values before the decimal point in answers I, II and III are irrelevant.
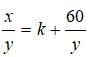
Notice that k is still the number of times that y goes into x evenly. 60/y is the decimal portion of the quotient, i.e. the remainder over the divisor y.
The first step to solving this problem is realizing that k, the number of times that y goes into x evenly, can be anything for this question since we are only given a value for the remainder. The integer values before the decimal point in answers I, II and III are irrelevant.
The decimal portion of the possible quotients in I, II and III are another story. From the equation we have above, for a decimal to be possible, it must be something that can be expressed as 60/y, since that is the portion of the quotient that corresponds to the decimal. But couldn't any decimal be expressed as 60 over some y? The answer is NO because we are told in the question that y is an integer.
Let's look at answer choice I first. Is 60 / y = 0.15, where y is an integer? This question is tantamount to asking if 60 is divisible by 0.15 or if 6000 is divisible by 15? 6000 IS divisible by 15 because it is divisible by 5 (ends in a 0) and by 3 (sum of digits, 6, is divisible by 3) Therefore, answer choice I is CORRECT. Using the same logic for answer choice II, we must check to see if 6000 is divisible by 16. 6000 IS divisible by 16 because it is can be divided by 2 four times: 3000, 1500, 750, 375. Therefore, answer choice II is CORRECT. 6000 IS NOT divisible by 17 because 17 is prime and not part of the prime make-up of 6000. Therefore answer choice III is NOT CORRECT. Therefore the correct answer is D, I and II only
Most Upvoted Answer
When the integer x is divided by the integer y, the remainder is 60. W...
|
Explore Courses for GMAT exam
|
|
Similar GMAT Doubts
Top Courses for GMATView all
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer?
Question Description
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer?.
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer?.
Solutions for When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possiblevalue of the quotient x/y?I. 15.15II. 18.16III. 17.17a)I onlyb)II onlyc)III onlyd)I and II onlye)I and III onlyCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup