GMAT Exam > GMAT Questions > S is the infinite sequence S1 = 2, S2 = 22, S...
Start Learning for Free
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?
- a)1
- b)2
- c)4
- d)6
- e)9
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–...
The first few terms of the sequence are 2, 22, and 222 and each subsequent term has an additional 2 added on. The 30th term then is a string of 30 2’s. If we line up the first 30 terms of the sequence to add them up, we will get rows in the following pattern:
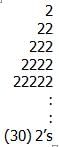
To find p, the sum of the first 30 terms of S, we would simply be adding columns of 2’s. The key here is to see a pattern in the addition process. Starting with the units digit column, all 30 of the terms have a 2 in that position so the sum of the units column would be 30 x 2 = 60. A zero would be written as the units digit of the sum and a six would be carried over to the tens column.
In the tens column, 29 of the 30 terms would have a 2 because the first term has no tens digit. The sum of the tens digits would be 29 x 2 = 58, to which we must add the 6 for a total of 64. The 4 gets written down as the second digit of p and the 6 is carried over to the hundreds column.
In the hundreds column, 28 of the 30 terms would have a 2, the sum of the hundreds digits would be 28 x 2 = 56, to which we must add the 6 again for a total of 62. The 2 gets written down as the third digit of p and the 6 is carried over to the thousands column.
There are two ways to finish this problem. We can do out the remaining 8 columns and find that the 11th digit (i.e. the 10 billions column) will have a sum of 2(20) + 4 = 44 (where the 4 was carried over from the 10th column). 4 then will be the 11th digit (from the right) of p (and a 4 will be carried over into the 12th column).
We could also have seen that each column has one less 2 than the previous, so if we started out with 30 2’s in the first column, the 11th column must have 11 – 1 = 10 less 2’s, for a total of 20 2’s. The amount that is carried over from the previous column could be calculated by realizing that the 10th column had 21 2’s for a total of 42. Since there is no way that the 10th column inherited more than 8 from the 9th column, the total must be forty-something and the amount that is carried over to the 11th column MUST BE 4. This makes the total for the 11th column 40 + 4 = 44 and the 11th digit of p4.
The correct answer is C.
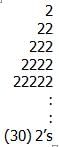
To find p, the sum of the first 30 terms of S, we would simply be adding columns of 2’s. The key here is to see a pattern in the addition process. Starting with the units digit column, all 30 of the terms have a 2 in that position so the sum of the units column would be 30 x 2 = 60. A zero would be written as the units digit of the sum and a six would be carried over to the tens column.
In the tens column, 29 of the 30 terms would have a 2 because the first term has no tens digit. The sum of the tens digits would be 29 x 2 = 58, to which we must add the 6 for a total of 64. The 4 gets written down as the second digit of p and the 6 is carried over to the hundreds column.
In the hundreds column, 28 of the 30 terms would have a 2, the sum of the hundreds digits would be 28 x 2 = 56, to which we must add the 6 again for a total of 62. The 2 gets written down as the third digit of p and the 6 is carried over to the thousands column.
There are two ways to finish this problem. We can do out the remaining 8 columns and find that the 11th digit (i.e. the 10 billions column) will have a sum of 2(20) + 4 = 44 (where the 4 was carried over from the 10th column). 4 then will be the 11th digit (from the right) of p (and a 4 will be carried over into the 12th column).
We could also have seen that each column has one less 2 than the previous, so if we started out with 30 2’s in the first column, the 11th column must have 11 – 1 = 10 less 2’s, for a total of 20 2’s. The amount that is carried over from the previous column could be calculated by realizing that the 10th column had 21 2’s for a total of 42. Since there is no way that the 10th column inherited more than 8 from the 9th column, the total must be forty-something and the amount that is carried over to the 11th column MUST BE 4. This makes the total for the 11th column 40 + 4 = 44 and the 11th digit of p4.
The correct answer is C.
Most Upvoted Answer
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–...
To find the value of Sk, let's look for a pattern in the sequence.
S1 = 2
S2 = 22
S3 = 222
...
From the given examples, we can see that each term Sk is formed by concatenating the number 2 a total of k times.
So, the pattern is that Sk is the number 2 repeated k times.
Therefore, Sk = 2 repeated k times.
For example:
S4 = 2222
S5 = 22222
and so on.
So, S is an infinite sequence where Sk = 2 repeated k times.
S1 = 2
S2 = 22
S3 = 222
...
From the given examples, we can see that each term Sk is formed by concatenating the number 2 a total of k times.
So, the pattern is that Sk is the number 2 repeated k times.
Therefore, Sk = 2 repeated k times.
For example:
S4 = 2222
S5 = 22222
and so on.
So, S is an infinite sequence where Sk = 2 repeated k times.

|
Explore Courses for GMAT exam
|

|
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer?
Question Description
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer?.
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer?.
Solutions for S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer?, a detailed solution for S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?a)1b)2c)4d)6e)9Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























