JEE Exam > JEE Questions > On dissolving 0.5 g of a non-volatile non-ion...
Start Learning for Free
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreases
from 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of the
solute is
(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)
from 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of the
solute is
(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)
Correct answer is '1.02'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benz...
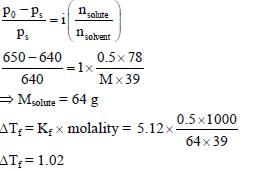
Most Upvoted Answer
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benz...
-1
, respectively)
We can use the equation for the depression of freezing point:
ΔTf = Kf · m
where ΔTf is the change in freezing point, Kf is the molal freezing point depression constant, and m is the molality of the solute.
First, we need to find the molality of the solute:
molality = moles of solute / mass of solvent (in kg)
The mass of benzene is 39 g, which is 0.039 kg. The molar mass of the solute is not given, so we cannot find the moles directly. However, we are given the mass of the solute, which is 0.5 g. We can assume that the solute is non-ionic and non-volatile, which means that it does not affect the vapor pressure of benzene. Therefore, we can use Raoult's law to find the moles of benzene:
Ptotal = Pbenzene + Psolute
where Ptotal is the total vapor pressure, Pbenzene is the vapor pressure of pure benzene, and Psolute is the vapor pressure of the solute (which is assumed to be zero). We are given that Pbenzene decreases from 650 mm Hg to 640 mm Hg, so the change in vapor pressure is:
ΔPbenzene = Pbenzene - Pbenzene,pure = 650 mm Hg - 760 mm Hg = -110 mm Hg
We can use the following equation to find the moles of benzene:
nbenzene = (Pbenzene / Patm) · V / RT
where Patm is the atmospheric pressure (which we assume to be 1 atm), V is the volume of benzene (which we assume to be equal to its mass divided by its density, 0.879 g/mL), R is the gas constant, and T is the temperature (which is not given, but we assume to be room temperature, around 25°C or 298 K).
Plugging in the values, we get:
nbenzene = (650 mm Hg / 760 mm Hg) · (0.039 kg / 0.879 g/mL) / (0.0821 L·atm/mol·K · 298 K) ≈ 0.0014 mol
Since the solute is non-volatile, its mass will not affect the vapor pressure of benzene. Therefore, we can assume that the new mass of benzene is still 39 g. The mass of the solute is 0.5 g, so the total mass of the solution is 39.5 g. The molality of the solute is:
molality = moles of solute / mass of solvent (in kg) = 0.5 g / 0.039 kg ≈ 12.8 mol/kg
Now we can use the equation for the depression of freezing point:
ΔTf = Kf · m
Plugging in the values, we get:
ΔTf = 5.12 K kg/mol · 12.8 mol/kg ≈ 65.5 K
Therefore, the depression of freezing point of benzene upon addition of the solute is approximately 65.5 K.
, respectively)
We can use the equation for the depression of freezing point:
ΔTf = Kf · m
where ΔTf is the change in freezing point, Kf is the molal freezing point depression constant, and m is the molality of the solute.
First, we need to find the molality of the solute:
molality = moles of solute / mass of solvent (in kg)
The mass of benzene is 39 g, which is 0.039 kg. The molar mass of the solute is not given, so we cannot find the moles directly. However, we are given the mass of the solute, which is 0.5 g. We can assume that the solute is non-ionic and non-volatile, which means that it does not affect the vapor pressure of benzene. Therefore, we can use Raoult's law to find the moles of benzene:
Ptotal = Pbenzene + Psolute
where Ptotal is the total vapor pressure, Pbenzene is the vapor pressure of pure benzene, and Psolute is the vapor pressure of the solute (which is assumed to be zero). We are given that Pbenzene decreases from 650 mm Hg to 640 mm Hg, so the change in vapor pressure is:
ΔPbenzene = Pbenzene - Pbenzene,pure = 650 mm Hg - 760 mm Hg = -110 mm Hg
We can use the following equation to find the moles of benzene:
nbenzene = (Pbenzene / Patm) · V / RT
where Patm is the atmospheric pressure (which we assume to be 1 atm), V is the volume of benzene (which we assume to be equal to its mass divided by its density, 0.879 g/mL), R is the gas constant, and T is the temperature (which is not given, but we assume to be room temperature, around 25°C or 298 K).
Plugging in the values, we get:
nbenzene = (650 mm Hg / 760 mm Hg) · (0.039 kg / 0.879 g/mL) / (0.0821 L·atm/mol·K · 298 K) ≈ 0.0014 mol
Since the solute is non-volatile, its mass will not affect the vapor pressure of benzene. Therefore, we can assume that the new mass of benzene is still 39 g. The mass of the solute is 0.5 g, so the total mass of the solution is 39.5 g. The molality of the solute is:
molality = moles of solute / mass of solvent (in kg) = 0.5 g / 0.039 kg ≈ 12.8 mol/kg
Now we can use the equation for the depression of freezing point:
ΔTf = Kf · m
Plugging in the values, we get:
ΔTf = 5.12 K kg/mol · 12.8 mol/kg ≈ 65.5 K
Therefore, the depression of freezing point of benzene upon addition of the solute is approximately 65.5 K.
Free Test
FREE
| Start Free Test |
Community Answer
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benz...
Yes, 1.02 is correct...
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.
|
Explore Courses for JEE exam
|
|
Top Courses for JEEView all
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer?
Question Description
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer?.
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer?.
Solutions for On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer?, a detailed solution for On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? has been provided alongside types of On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreasesfrom 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of thesolute is(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol-1 and 5.12 K kg mol–1, respectively)Correct answer is '1.02'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup