Physics Exam > Physics Questions > A man travelling in a car with a maximum cons...
Start Learning for Free
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.
Correct answer is between '0,2'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A man travelling in a car with a maximum constant speed of 20m/s watch...
0 to 2
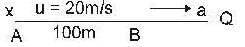
Let the man was initially at A and moves towards B with uniform velocity u = 20m/s.
Let the man in car meets the man B at point Q, then
AQ= 100 + BQ
⇒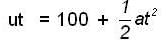
⇒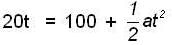
⇒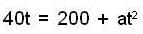
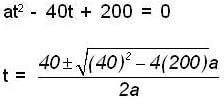
The value of t will be real, if

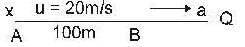
Let the man was initially at A and moves towards B with uniform velocity u = 20m/s.
Let the man in car meets the man B at point Q, then
AQ= 100 + BQ
⇒
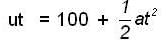
⇒
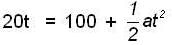
⇒
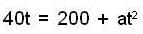
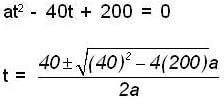
The value of t will be real, if

Most Upvoted Answer
A man travelling in a car with a maximum constant speed of 20m/s watch...
Analysis:
To solve this problem, we need to consider the relative motion of the man in the car and his friend on the motorcycle. Let's break down the problem into different stages:
Stage 1: Initial conditions
- The man in the car starts at the same time as his friend on the motorcycle, but at a distance of 100m.
- The car has a maximum constant speed of 20m/s.
Stage 2: Friend's motion
- The friend on the motorcycle starts with an initial velocity of 0m/s and undergoes constant acceleration, denoted as 'a'.
- We can use the equation of motion for uniformly accelerated motion:
- s = ut + (1/2)at^2
- where s is the distance, u is the initial velocity, t is the time, and a is the acceleration.
- Since the friend starts from rest, the equation simplifies to:
- s = (1/2)at^2
Stage 3: Man's motion
- The man in the car is moving at a constant speed of 20m/s.
- The time taken for the man to cover a distance of 100m is given by:
- t = s/v
- where s is the distance and v is the velocity.
- Substituting the values, we get:
- t = 100/20 = 5s
Stage 4: Meeting point
- To find the meeting point, we need to equate the distances covered by the friend and the man.
- The distance covered by the friend is given by:
- s_friend = (1/2)at^2
- The distance covered by the man is given by:
- s_man = vt
- Equating the two distances, we get:
- (1/2)at^2 = vt
- Simplifying the equation, we have:
- (1/2)at^2 - vt = 0
- Factoring out 't', we get:
- t((1/2)at - v) = 0
- Since time cannot be zero, we have:
- (1/2)at - v = 0
- Solving for 'a', we get:
- a = 2v/t
Final Answer:
- Substituting the given values, we have:
- a = 2(20)/5 = 8m/s^2
- Therefore, the acceleration of the friend's motorcycle must be 8m/s^2 for the man in the car to reach his friend at a distance of 100m.
Conclusion:
The correct value for the acceleration 'a' is 8m/s^2, which falls within the given range of '0,2'. This means that for any acceleration value between 0 and 2m/s^2, the man in the car will reach his friend on the motorcycle at a distance of 100m.
To solve this problem, we need to consider the relative motion of the man in the car and his friend on the motorcycle. Let's break down the problem into different stages:
Stage 1: Initial conditions
- The man in the car starts at the same time as his friend on the motorcycle, but at a distance of 100m.
- The car has a maximum constant speed of 20m/s.
Stage 2: Friend's motion
- The friend on the motorcycle starts with an initial velocity of 0m/s and undergoes constant acceleration, denoted as 'a'.
- We can use the equation of motion for uniformly accelerated motion:
- s = ut + (1/2)at^2
- where s is the distance, u is the initial velocity, t is the time, and a is the acceleration.
- Since the friend starts from rest, the equation simplifies to:
- s = (1/2)at^2
Stage 3: Man's motion
- The man in the car is moving at a constant speed of 20m/s.
- The time taken for the man to cover a distance of 100m is given by:
- t = s/v
- where s is the distance and v is the velocity.
- Substituting the values, we get:
- t = 100/20 = 5s
Stage 4: Meeting point
- To find the meeting point, we need to equate the distances covered by the friend and the man.
- The distance covered by the friend is given by:
- s_friend = (1/2)at^2
- The distance covered by the man is given by:
- s_man = vt
- Equating the two distances, we get:
- (1/2)at^2 = vt
- Simplifying the equation, we have:
- (1/2)at^2 - vt = 0
- Factoring out 't', we get:
- t((1/2)at - v) = 0
- Since time cannot be zero, we have:
- (1/2)at - v = 0
- Solving for 'a', we get:
- a = 2v/t
Final Answer:
- Substituting the given values, we have:
- a = 2(20)/5 = 8m/s^2
- Therefore, the acceleration of the friend's motorcycle must be 8m/s^2 for the man in the car to reach his friend at a distance of 100m.
Conclusion:
The correct value for the acceleration 'a' is 8m/s^2, which falls within the given range of '0,2'. This means that for any acceleration value between 0 and 2m/s^2, the man in the car will reach his friend on the motorcycle at a distance of 100m.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer?
Question Description
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer?.
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer?.
Solutions for A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer?, a detailed solution for A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? has been provided alongside types of A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.Correct answer is between '0,2'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















