Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A completely mixed dilute suspension of sand ...
Start Learning for Free
A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.
Correct answer is '0.35'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A completely mixed dilute suspension of sand particles having diameter...
As we know that settling velocity for discrete particles is given by stokes law as-
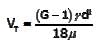
⇒ Vτ ∞ dt
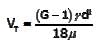
⇒ Vτ ∞ dt
For 30 second duration if 0.35 mm particle size settles completely then % removal of particle size 0.45 mm and 0.50 mm will be 100% respectively for each. As settling velocity of particle size 0.45 mm and 0.50 mm will be greater than settling velocity of size 0.35
mm (Vτ ∞ dt).
mm (Vτ ∞ dt).
Most Upvoted Answer
A completely mixed dilute suspension of sand particles having diameter...
Given information:
- Diameter of the glass column = 10 cm
- Height of the glass column = 2.50 m
- Diameters of sand particles in the suspension = 0.25, 0.35, 0.40, 0.45, and 0.50 mm
Objective:
To determine the percentage removal of particles with diameters 0.45 mm and 0.50 mm after 30 seconds of settling.
The volume of the glass column can be calculated using the formula for the volume of a cylinder:
Volume = π * (radius)^2 * height
Given that the diameter of the column is 10 cm, the radius (r) can be calculated as:
radius = diameter / 2 = 10 cm / 2 = 5 cm = 0.05 m
Substituting the values into the formula, we get:
Volume = π * (0.05 m)^2 * 2.50 m = 0.01963 m^3
The settling velocity of a particle can be calculated using Stokes' law:
V = (2/9) * (d^2) * (ρp - ρf) / η
Where:
V = Settling velocity of the particle (m/s)
d = Diameter of the particle (m)
ρp = Density of the particle (kg/m^3)
ρf = Density of the fluid (kg/m^3)
η = Dynamic viscosity of the fluid (Pa.s)
Given that the density of sand particles is approximately 2650 kg/m^3 and the dynamic viscosity of water is approximately 0.001 Pa.s, we can calculate the settling velocity of the 0.35 mm particles:
V_0.35 = (2/9) * (0.00035 m)^2 * (2650 kg/m^3 - 1000 kg/m^3) / 0.001 Pa.s ≈ 0.0069 m/s
The settling distance can be calculated using the formula:
Distance = Velocity * Time
Given that the settling time is 30 seconds, we can calculate the settling distance of the 0.35 mm particles:
Distance_0.35 = 0.0069 m/s * 30 s = 0.207 m
To calculate the percentage removal of particles with diameters 0.45 mm and 0.50 mm, we need to determine the settling distance for these particles as well.
Using the settling velocity formula, we can calculate the settling velocities for the 0.45 mm and 0.50 mm particles:
V_0.45 = (2/9) * (0.00045 m)^2 * (2650 kg/m^3 - 1000 kg/m^3) / 0.001 Pa.s ≈ 0.013 m/s
V_0.50 = (2/9) * (0.0005 m)^2 * (2650 kg/m^3 - 1000 kg
- Diameter of the glass column = 10 cm
- Height of the glass column = 2.50 m
- Diameters of sand particles in the suspension = 0.25, 0.35, 0.40, 0.45, and 0.50 mm
Objective:
To determine the percentage removal of particles with diameters 0.45 mm and 0.50 mm after 30 seconds of settling.
Calculation:
1. Calculation of the volume of the glass column:
The volume of the glass column can be calculated using the formula for the volume of a cylinder:
Volume = π * (radius)^2 * height
Given that the diameter of the column is 10 cm, the radius (r) can be calculated as:
radius = diameter / 2 = 10 cm / 2 = 5 cm = 0.05 m
Substituting the values into the formula, we get:
Volume = π * (0.05 m)^2 * 2.50 m = 0.01963 m^3
2. Calculation of the settling velocity:
The settling velocity of a particle can be calculated using Stokes' law:
V = (2/9) * (d^2) * (ρp - ρf) / η
Where:
V = Settling velocity of the particle (m/s)
d = Diameter of the particle (m)
ρp = Density of the particle (kg/m^3)
ρf = Density of the fluid (kg/m^3)
η = Dynamic viscosity of the fluid (Pa.s)
Given that the density of sand particles is approximately 2650 kg/m^3 and the dynamic viscosity of water is approximately 0.001 Pa.s, we can calculate the settling velocity of the 0.35 mm particles:
V_0.35 = (2/9) * (0.00035 m)^2 * (2650 kg/m^3 - 1000 kg/m^3) / 0.001 Pa.s ≈ 0.0069 m/s
3. Calculation of the settling distance:
The settling distance can be calculated using the formula:
Distance = Velocity * Time
Given that the settling time is 30 seconds, we can calculate the settling distance of the 0.35 mm particles:
Distance_0.35 = 0.0069 m/s * 30 s = 0.207 m
4. Calculation of the percentage removal:
To calculate the percentage removal of particles with diameters 0.45 mm and 0.50 mm, we need to determine the settling distance for these particles as well.
Using the settling velocity formula, we can calculate the settling velocities for the 0.45 mm and 0.50 mm particles:
V_0.45 = (2/9) * (0.00045 m)^2 * (2650 kg/m^3 - 1000 kg/m^3) / 0.001 Pa.s ≈ 0.013 m/s
V_0.50 = (2/9) * (0.0005 m)^2 * (2650 kg/m^3 - 1000 kg
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer?
Question Description
A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer?.
A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer?.
Solutions for A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer?, a detailed solution for A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? has been provided alongside types of A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A completely mixed dilute suspension of sand particles having diameters 0.25, 0.35, 0.40, 0.45 and 0.50mm are filled in a transparent glass column of diameter 10 cm and height 2.50 m. The suspension is allowed to settle without any disturbance. It is observed that all particles of diameter 0.35 mm settle to the bottom of the column in 30 s. For the same period of 30s, the percentage removal (round off to integer value) of particles of diameters 0.45 and 0.50 mm from the suspension is _____________.Correct answer is '0.35'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup