Physics Exam > Physics Questions > Find the rank of the matrix for the following...
Start Learning for Free
Find the rank of the matrix for the following equations :
4x + 2y + z + 3u = 0
6x + 3y + 4z + 7u = 0
2x + y + u = 0
4x + 2y + z + 3u = 0
6x + 3y + 4z + 7u = 0
2x + y + u = 0
Correct answer is '2'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Find the rank of the matrix for the following equations :4x + 2y + z +...
Consider the augmented matrix, [A : O] where A the coefficient matrix,

interchanging the variables x and z
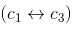
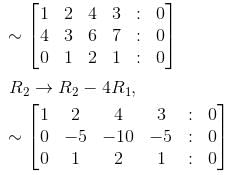

∴ The rank of the matrix is 2.
The correct answer is: 2
Most Upvoted Answer
Find the rank of the matrix for the following equations :4x + 2y + z +...
< b="" />Rank of a matrix:
The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix. It represents the dimension of the vector space spanned by the rows or columns of the matrix.
< b="" />Solution:
To find the rank of the given matrix, we need to perform row operations to reduce the matrix to its row echelon form or reduced row echelon form.
< b="" />Step 1: Write the augmented matrix:
We write the given system of equations as an augmented matrix. The augmented matrix is obtained by writing the coefficients of the variables in the system of equations.
The augmented matrix for the given system of equations is:
[ 4 2 1 3 | 0 ]
[ 6 3 4 7 | 0 ]
[ 2 1 0 1 | 0 ]
< b="" />Step 2: Perform row operations:
We perform row operations to reduce the augmented matrix to its row echelon form or reduced row echelon form.
- Row 2 = Row 2 - 3/2 * Row 1
- Row 3 = Row 3 - 1/2 * Row 1
The updated augmented matrix is:
[ 4 2 1 3 | 0 ]
[ 0 0 7/2 7/2 | 0 ]
[ 0 0 -1/2 -1/2 | 0 ]
< b="" />Step 3: Continue row operations:
We continue performing row operations to further reduce the augmented matrix.
- Row 2 = Row 2 * 2/7
- Row 3 = Row 3 * (-2)
The updated augmented matrix is:
[ 4 2 1 3 | 0 ]
[ 0 0 1 1 | 0 ]
[ 0 0 1 1 | 0 ]
< b="" />Step 4: Final row operations:
We perform final row operations to obtain the row echelon form or reduced row echelon form.
- Row 1 = Row 1 - Row 3
- Row 2 = Row 2 - Row 3
The final augmented matrix is:
[ 4 2 0 2 | 0 ]
[ 0 0 0 0 | 0 ]
[ 0 0 1 1 | 0 ]
< b="" />Step 5: Count the number of non-zero rows:
We count the number of non-zero rows in the row echelon form or reduced row echelon form of the augmented matrix.
In this case, there are 2 non-zero rows.
< b="" />Step 6: Conclusion:
The rank of the matrix is the number of non-zero rows in the row echelon form or reduced row echelon form of the augmented matrix.
Therefore, the rank of the given matrix is 2.
The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix. It represents the dimension of the vector space spanned by the rows or columns of the matrix.
< b="" />Solution:
To find the rank of the given matrix, we need to perform row operations to reduce the matrix to its row echelon form or reduced row echelon form.
< b="" />Step 1: Write the augmented matrix:
We write the given system of equations as an augmented matrix. The augmented matrix is obtained by writing the coefficients of the variables in the system of equations.
The augmented matrix for the given system of equations is:
[ 4 2 1 3 | 0 ]
[ 6 3 4 7 | 0 ]
[ 2 1 0 1 | 0 ]
< b="" />Step 2: Perform row operations:
We perform row operations to reduce the augmented matrix to its row echelon form or reduced row echelon form.
- Row 2 = Row 2 - 3/2 * Row 1
- Row 3 = Row 3 - 1/2 * Row 1
The updated augmented matrix is:
[ 4 2 1 3 | 0 ]
[ 0 0 7/2 7/2 | 0 ]
[ 0 0 -1/2 -1/2 | 0 ]
< b="" />Step 3: Continue row operations:
We continue performing row operations to further reduce the augmented matrix.
- Row 2 = Row 2 * 2/7
- Row 3 = Row 3 * (-2)
The updated augmented matrix is:
[ 4 2 1 3 | 0 ]
[ 0 0 1 1 | 0 ]
[ 0 0 1 1 | 0 ]
< b="" />Step 4: Final row operations:
We perform final row operations to obtain the row echelon form or reduced row echelon form.
- Row 1 = Row 1 - Row 3
- Row 2 = Row 2 - Row 3
The final augmented matrix is:
[ 4 2 0 2 | 0 ]
[ 0 0 0 0 | 0 ]
[ 0 0 1 1 | 0 ]
< b="" />Step 5: Count the number of non-zero rows:
We count the number of non-zero rows in the row echelon form or reduced row echelon form of the augmented matrix.
In this case, there are 2 non-zero rows.
< b="" />Step 6: Conclusion:
The rank of the matrix is the number of non-zero rows in the row echelon form or reduced row echelon form of the augmented matrix.
Therefore, the rank of the given matrix is 2.
Free Test
FREE
| Start Free Test |
Community Answer
Find the rank of the matrix for the following equations :4x + 2y + z +...
When we chagen matrix in eclane form or normal form then we can find rank 2 of given matrix

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer?
Question Description
Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer?.
Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer?.
Solutions for Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer?, a detailed solution for Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? has been provided alongside types of Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Find the rank of the matrix for the following equations :4x + 2y + z + 3u = 06x + 3y + 4z + 7u = 02x + y + u = 0Correct answer is '2'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















