Physics Exam > Physics Questions > Trigonometric Fourier series of a periodic ti...
Start Learning for Free
Trigonometric Fourier series of a periodic time function can have only
Select one:
Select one:
- a)Cosine and sine terms
- b)dc and cosine terms
- c)Cosine terms
- d)Sine terms
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Trigonometric Fourier series of a periodic time function can have only...
The Fourier series of a periodic function x(t) is given by the form
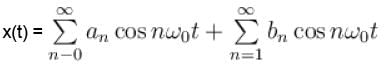
Thus the series has cosine terms of all harmonics :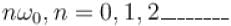
The correct answer is: Cosine terms
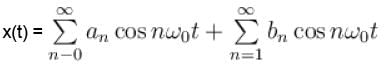
Thus the series has cosine terms of all harmonics :
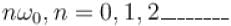
The correct answer is: Cosine terms
 This question is part of UPSC exam. View all Physics courses
This question is part of UPSC exam. View all Physics courses
Most Upvoted Answer
Trigonometric Fourier series of a periodic time function can have only...
Trigonometric Fourier series
The trigonometric Fourier series is a mathematical representation of a periodic time function using cosine and sine terms. It allows us to express any periodic function as a sum of sinusoidal functions with different frequencies and amplitudes. The general form of a trigonometric Fourier series is given by:
f(t) = a0 + Σ(an * cos(nωt) + bn * sin(nωt))
where f(t) is the periodic function, t is the time, a0 is the DC (direct current) term, an and bn are the Fourier coefficients, n is the harmonic number, and ω is the angular frequency.
DC term
The DC term represents the average value of the periodic function over one period. It is a constant term that is unaffected by the frequency components of the function. In the trigonometric Fourier series, the DC term is represented by a0.
Cosine terms
The cosine terms in the series represent the even components of the periodic function. They have frequencies that are integer multiples of the fundamental frequency, ω. The coefficients an determine the amplitudes of the cosine terms.
Sine terms
The sine terms in the series represent the odd components of the periodic function. They also have frequencies that are integer multiples of the fundamental frequency, ω. The coefficients bn determine the amplitudes of the sine terms.
Explanation of the answer
The correct answer is option 'C', which states that the trigonometric Fourier series of a periodic time function can have only cosine terms. This means that the function being represented does not have any odd components or sine terms in its Fourier series.
The absence of sine terms implies that the function is symmetric about the vertical axis or has an even symmetry. In such cases, the Fourier coefficients bn representing the amplitudes of the sine terms will be zero.
Therefore, the trigonometric Fourier series will only contain cosine terms, which represent the even components of the function. This is consistent with the even symmetry of the function.
It is important to note that the absence of sine terms does not mean that there are no odd components in the function. It simply means that these odd components can be expressed as combinations of the cosine terms using trigonometric identities.
In summary, the trigonometric Fourier series of a periodic time function can have only cosine terms when the function has an even symmetry or is symmetric about the vertical axis.
The trigonometric Fourier series is a mathematical representation of a periodic time function using cosine and sine terms. It allows us to express any periodic function as a sum of sinusoidal functions with different frequencies and amplitudes. The general form of a trigonometric Fourier series is given by:
f(t) = a0 + Σ(an * cos(nωt) + bn * sin(nωt))
where f(t) is the periodic function, t is the time, a0 is the DC (direct current) term, an and bn are the Fourier coefficients, n is the harmonic number, and ω is the angular frequency.
DC term
The DC term represents the average value of the periodic function over one period. It is a constant term that is unaffected by the frequency components of the function. In the trigonometric Fourier series, the DC term is represented by a0.
Cosine terms
The cosine terms in the series represent the even components of the periodic function. They have frequencies that are integer multiples of the fundamental frequency, ω. The coefficients an determine the amplitudes of the cosine terms.
Sine terms
The sine terms in the series represent the odd components of the periodic function. They also have frequencies that are integer multiples of the fundamental frequency, ω. The coefficients bn determine the amplitudes of the sine terms.
Explanation of the answer
The correct answer is option 'C', which states that the trigonometric Fourier series of a periodic time function can have only cosine terms. This means that the function being represented does not have any odd components or sine terms in its Fourier series.
The absence of sine terms implies that the function is symmetric about the vertical axis or has an even symmetry. In such cases, the Fourier coefficients bn representing the amplitudes of the sine terms will be zero.
Therefore, the trigonometric Fourier series will only contain cosine terms, which represent the even components of the function. This is consistent with the even symmetry of the function.
It is important to note that the absence of sine terms does not mean that there are no odd components in the function. It simply means that these odd components can be expressed as combinations of the cosine terms using trigonometric identities.
In summary, the trigonometric Fourier series of a periodic time function can have only cosine terms when the function has an even symmetry or is symmetric about the vertical axis.
Community Answer
Trigonometric Fourier series of a periodic time function can have only...
I think it ans is first because fourier series is any periodic is given by
and it contain cosine and sin term both so how could c is correct i don't know here we don't talk about any even or odd function in it .just simply ask

|
Explore Courses for Physics exam
|

|
Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer?
Question Description
Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer?.
Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Trigonometric Fourier series of a periodic time function can have onlySelect one:a)Cosine and sine termsb)dc and cosine termsc)Cosine termsd)Sine termsCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


 and it contain cosine and sin term both so how could c is correct i don't know here we don't talk about any even or odd function in it .just simply ask
and it contain cosine and sin term both so how could c is correct i don't know here we don't talk about any even or odd function in it .just simply ask 














