Physics Exam > Physics Questions > At standard temperature and pressure, the den...
Start Learning for Free
At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?
Correct answer is '5'. Can you explain this answer?
Verified Answer
At standard temperature and pressure, the density of a gas is 1.3 kg/m...
Velocity of sound vs = 330 m/s
Density of gas ρ = 1.5kg/m3
Atmosphere Pressure p = 1.01 × 105 N/m2
Substituting these values in
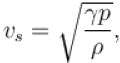 we get
we get
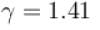
Now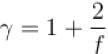
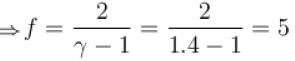
The correct answer is: 5
Density of gas ρ = 1.5kg/m3
Atmosphere Pressure p = 1.01 × 105 N/m2
Substituting these values in
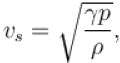 we get
we get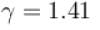
Now
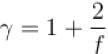
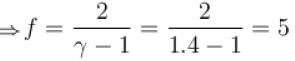
The correct answer is: 5
Most Upvoted Answer
At standard temperature and pressure, the density of a gas is 1.3 kg/m...
Density of the gas:
At standard temperature and pressure (STP), the density of the gas is given as 1.3 kg/m3. This means that for every cubic meter of the gas, there is a mass of 1.3 kg present.
Speed of sound in the gas:
The speed of sound in the gas is given as 330 m/s. This represents the velocity at which sound waves propagate through the gas.
Degree of freedom:
The degree of freedom of a gas refers to the number of independent ways in which the gas molecules can move or store energy. It is closely related to the number of translational, rotational, and vibrational motions available to the gas molecules.
To determine the degree of freedom of the gas, we can use the relationship between the speed of sound, the density, and the degree of freedom. The formula is given as:
v = sqrt((gamma * R * T) / M)
where:
v = speed of sound
gamma = ratio of specific heat capacities
R = gas constant
T = temperature
M = molar mass of the gas
Derivation:
1. First, we rearrange the formula to solve for the degree of freedom:
degree of freedom = (v^2 * M) / (gamma * R * T)
2. Next, we substitute the given values into the formula:
v = 330 m/s
M = ? (molar mass of the gas is not given)
gamma = ? (ratio of specific heat capacities is not given)
R = ? (gas constant is not given)
T = ? (temperature is not given)
Since the molar mass, ratio of specific heat capacities, gas constant, and temperature are not given, we cannot directly calculate the degree of freedom using the given information.
At standard temperature and pressure (STP), the density of the gas is given as 1.3 kg/m3. This means that for every cubic meter of the gas, there is a mass of 1.3 kg present.
Speed of sound in the gas:
The speed of sound in the gas is given as 330 m/s. This represents the velocity at which sound waves propagate through the gas.
Degree of freedom:
The degree of freedom of a gas refers to the number of independent ways in which the gas molecules can move or store energy. It is closely related to the number of translational, rotational, and vibrational motions available to the gas molecules.
To determine the degree of freedom of the gas, we can use the relationship between the speed of sound, the density, and the degree of freedom. The formula is given as:
v = sqrt((gamma * R * T) / M)
where:
v = speed of sound
gamma = ratio of specific heat capacities
R = gas constant
T = temperature
M = molar mass of the gas
Derivation:
1. First, we rearrange the formula to solve for the degree of freedom:
degree of freedom = (v^2 * M) / (gamma * R * T)
2. Next, we substitute the given values into the formula:
v = 330 m/s
M = ? (molar mass of the gas is not given)
gamma = ? (ratio of specific heat capacities is not given)
R = ? (gas constant is not given)
T = ? (temperature is not given)
Since the molar mass, ratio of specific heat capacities, gas constant, and temperature are not given, we cannot directly calculate the degree of freedom using the given information.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer?
Question Description
At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer?.
At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer?.
Solutions for At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer?, a detailed solution for At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? has been provided alongside types of At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice At standard temperature and pressure, the density of a gas is 1.3 kg/m3 and the speed of the sound and the speed of the sound in gas is 330 m/s. Then the degree of freedom of the gas will be?Correct answer is '5'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















