Physics Exam > Physics Questions > The mean internal energy of a one-dimensional...
Start Learning for Free
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.
Correct answer is '1'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The mean internal energy of a one-dimensional harmonic oscillator in e...
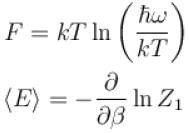
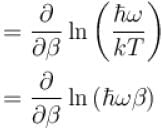

The correct answer is: 1
Most Upvoted Answer
The mean internal energy of a one-dimensional harmonic oscillator in e...
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is indeed equal to 1 in the units of kBT. Let's understand this concept in detail:
Harmonic Oscillator:
A harmonic oscillator is a system that exhibits simple harmonic motion, which is characterized by a restoring force that is directly proportional to the displacement from the equilibrium position. In the case of a one-dimensional harmonic oscillator, the potential energy is given by the equation U(x) = 1/2 kx^2, where k is the spring constant and x is the displacement from the equilibrium position.
Internal Energy:
The internal energy of a system refers to the total energy associated with the microscopic motion and interactions of particles within the system. In the case of a harmonic oscillator, the internal energy is directly related to the potential energy of the system.
Equilibrium with a Heat Bath:
When a harmonic oscillator is in equilibrium with a heat bath, it means that the system is in thermal equilibrium with its surroundings and exchanging energy in the form of heat. The heat bath provides a constant temperature T to the harmonic oscillator.
Mean Internal Energy:
The mean internal energy, denoted by, represents the average value of the internal energy over a large number of oscillations. It is given by the formula = (1/2) kBT, where kB is the Boltzmann constant.
Explanation:
The mean internal energy of the harmonic oscillator in equilibrium with a heat bath of temperature T is 1 in the units of kBT. This means that on average, the internal energy of the system is equal to kBT/2.
The factor of 1/2 arises from the equipartition theorem, which states that each degree of freedom of a system in thermal equilibrium contributes an average energy of (1/2) kBT. In the case of a one-dimensional harmonic oscillator, there is only one degree of freedom associated with its motion along the x-axis.
Since the potential energy of a one-dimensional harmonic oscillator is given by U(x) = 1/2 kx^2, the average potential energy is (1/2) k, where represents the mean square displacement. This mean square displacement is directly related to the temperature T and is equal to kB T / k.
Substituting this value into the average potential energy equation, we get (1/2) k = (1/2) kBT.
Thus, the mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is 1 in the units of kBT.
Harmonic Oscillator:
A harmonic oscillator is a system that exhibits simple harmonic motion, which is characterized by a restoring force that is directly proportional to the displacement from the equilibrium position. In the case of a one-dimensional harmonic oscillator, the potential energy is given by the equation U(x) = 1/2 kx^2, where k is the spring constant and x is the displacement from the equilibrium position.
Internal Energy:
The internal energy of a system refers to the total energy associated with the microscopic motion and interactions of particles within the system. In the case of a harmonic oscillator, the internal energy is directly related to the potential energy of the system.
Equilibrium with a Heat Bath:
When a harmonic oscillator is in equilibrium with a heat bath, it means that the system is in thermal equilibrium with its surroundings and exchanging energy in the form of heat. The heat bath provides a constant temperature T to the harmonic oscillator.
Mean Internal Energy:
The mean internal energy, denoted by
Explanation:
The mean internal energy of the harmonic oscillator in equilibrium with a heat bath of temperature T is 1 in the units of kBT. This means that on average, the internal energy of the system is equal to kBT/2.
The factor of 1/2 arises from the equipartition theorem, which states that each degree of freedom of a system in thermal equilibrium contributes an average energy of (1/2) kBT. In the case of a one-dimensional harmonic oscillator, there is only one degree of freedom associated with its motion along the x-axis.
Since the potential energy of a one-dimensional harmonic oscillator is given by U(x) = 1/2 kx^2, the average potential energy is (1/2) k
Substituting this value into the average potential energy equation, we get (1/2) k
Thus, the mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is 1 in the units of kBT.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer?
Question Description
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer?.
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer?.
Solutions for The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer?, a detailed solution for The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? has been provided alongside types of The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The mean internal energy of a one-dimensional harmonic oscillator in equilibrium with a heat bath of temperature T is in the units of kBT.Correct answer is '1'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















