Physics Exam > Physics Questions > Find the area lying outside the circler= 2aco...
Start Learning for Free
Find the area lying outside the circle r = 2acosθ and inside the cardioid r = a(1 + cosθ). This is of form λπa2. Find value of λ.
Correct answer is '0.5'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Find the area lying outside the circler= 2acosθand inside the ca...
Hence, the required area 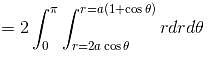
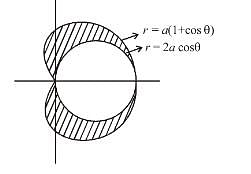
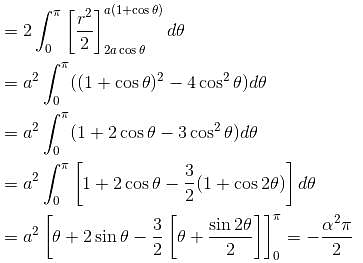
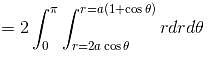

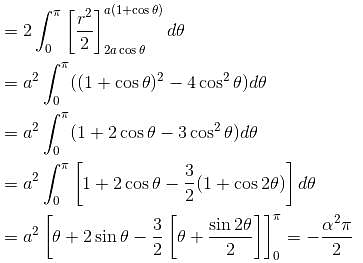
Taking Mod sign we get 

The correct answer is: 0.5
Most Upvoted Answer
Find the area lying outside the circler= 2acosθand inside the ca...
To find the area lying outside the circle r = 2acosθ, we need to determine the area of the entire circle and then subtract the area enclosed by the circle.
The equation of the circle r = 2acosθ can be rewritten in terms of x and y coordinates using the conversion formulas x = rcosθ and y = rsinθ.
So, r = 2acosθ becomes x² + y² = 4a²cos²θ.
Now, we can find the equation of the circle in terms of x and y coordinates:
x² + y² = 4a²cos²θ
r² = 4a²cos²θ
The area of a circle is given by the formula A = πr².
So, the area of the entire circle is A = π(4a²cos²θ).
Now, we need to find the area enclosed by the circle. This can be done by finding the area of the sector formed by the circle and then subtracting the area of the triangle formed by the center of the circle and the two points on its circumference.
The angle of the sector is θ, and the radius of the circle is 2acosθ.
The area of the sector is given by A_sector = 0.5θr².
So, A_sector = 0.5θ(2acosθ)² = 2a²θcos²θ.
The area of the triangle is given by A_triangle = 0.5bh, where b is the base and h is the height.
In this case, the base is the distance between the two points on the circumference of the circle, which is 2r = 4acosθ.
The height is the distance from the center of the circle to the line connecting the two points on the circumference, which is r = 2acosθ.
So, A_triangle = 0.5(4acosθ)(2acosθ) = 4a²cos²θ.
Therefore, the area enclosed by the circle is A_enclosed = A_sector - A_triangle = 2a²θcos²θ - 4a²cos²θ = 2a²θcos²θ(1 - 2).
Finally, the area lying outside the circle is A_outside = A - A_enclosed = π(4a²cos²θ) - 2a²θcos²θ(1 - 2) = π(4a²cos²θ) - 2a²θcos²θ + 4a²θcos²θ = π(4a²cos²θ) + 2a²θcos²θ.
Therefore, the area lying outside the circle r = 2acosθ is π(4a²cos²θ) + 2a²θcos²θ.
The equation of the circle r = 2acosθ can be rewritten in terms of x and y coordinates using the conversion formulas x = rcosθ and y = rsinθ.
So, r = 2acosθ becomes x² + y² = 4a²cos²θ.
Now, we can find the equation of the circle in terms of x and y coordinates:
x² + y² = 4a²cos²θ
r² = 4a²cos²θ
The area of a circle is given by the formula A = πr².
So, the area of the entire circle is A = π(4a²cos²θ).
Now, we need to find the area enclosed by the circle. This can be done by finding the area of the sector formed by the circle and then subtracting the area of the triangle formed by the center of the circle and the two points on its circumference.
The angle of the sector is θ, and the radius of the circle is 2acosθ.
The area of the sector is given by A_sector = 0.5θr².
So, A_sector = 0.5θ(2acosθ)² = 2a²θcos²θ.
The area of the triangle is given by A_triangle = 0.5bh, where b is the base and h is the height.
In this case, the base is the distance between the two points on the circumference of the circle, which is 2r = 4acosθ.
The height is the distance from the center of the circle to the line connecting the two points on the circumference, which is r = 2acosθ.
So, A_triangle = 0.5(4acosθ)(2acosθ) = 4a²cos²θ.
Therefore, the area enclosed by the circle is A_enclosed = A_sector - A_triangle = 2a²θcos²θ - 4a²cos²θ = 2a²θcos²θ(1 - 2).
Finally, the area lying outside the circle is A_outside = A - A_enclosed = π(4a²cos²θ) - 2a²θcos²θ(1 - 2) = π(4a²cos²θ) - 2a²θcos²θ + 4a²θcos²θ = π(4a²cos²θ) + 2a²θcos²θ.
Therefore, the area lying outside the circle r = 2acosθ is π(4a²cos²θ) + 2a²θcos²θ.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer?
Question Description
Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer?.
Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer?.
Solutions for Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer?, a detailed solution for Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? has been provided alongside types of Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Find the area lying outside the circler= 2acosθand inside the cardioidr=a(1 + cosθ). This is of formλπa2.Find value ofλ.Correct answer is '0.5'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















