Physics Exam > Physics Questions > The efficiency of the Carnot cycle may be inc...
Start Learning for Free
The efficiency of the Carnot cycle may be increased by.
Select one:
Select one:
- a)increasing the lowest temperature
- b)decreasing the highest temperature
- c)Keeping the lowest temperature constant
- d)decreasing the lowest temperature
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The efficiency of the Carnot cycle may be increased by.Select one:a)in...
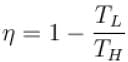
if TL is reduced, η can be increased.
The correct answer is: decreasing the lowest temperature
Most Upvoted Answer
The efficiency of the Carnot cycle may be increased by.Select one:a)in...
The Efficiency of the Carnot Cycle may be increased by decreasing the lowest temperature.
Introduction:
The Carnot cycle is a theoretical thermodynamic cycle that provides the maximum possible efficiency for a heat engine operating between two temperatures. It consists of four reversible processes: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression. The efficiency of the Carnot cycle is given by the expression:
Efficiency = 1 - (Tc/Th)
Where Tc is the absolute temperature of the cold reservoir and Th is the absolute temperature of the hot reservoir.
Explanation:
To understand why decreasing the lowest temperature (Tc) increases the efficiency of the Carnot cycle, let's consider the expression for efficiency:
Efficiency = 1 - (Tc/Th)
Effect of decreasing the lowest temperature:
When the lowest temperature (Tc) is decreased while keeping the highest temperature (Th) constant, the value of the term (Tc/Th) decreases. As a result, the efficiency of the Carnot cycle increases.
Reasoning:
There are two main reasons why decreasing the lowest temperature increases the efficiency of the Carnot cycle:
1. Increased temperature difference:
The efficiency of a heat engine is directly proportional to the temperature difference between the hot and cold reservoirs. By decreasing the lowest temperature (Tc), the temperature difference (Th - Tc) increases. This larger temperature difference allows for a greater conversion of heat into work, resulting in a higher efficiency.
2. Reduced heat loss:
Heat engines operate by extracting heat from the hot reservoir and rejecting heat to the cold reservoir. However, some heat is inevitably lost to the surroundings during this process. By decreasing the lowest temperature (Tc), the temperature difference between the heat engine and the surroundings also decreases, reducing the amount of heat lost. This reduction in heat loss contributes to an increase in efficiency.
Conclusion:
In conclusion, the efficiency of the Carnot cycle can be increased by decreasing the lowest temperature (Tc). This decrease results in a larger temperature difference between the hot and cold reservoirs, allowing for a greater conversion of heat into work. Additionally, reducing the lowest temperature helps to minimize heat loss to the surroundings, further improving the efficiency of the cycle.
Introduction:
The Carnot cycle is a theoretical thermodynamic cycle that provides the maximum possible efficiency for a heat engine operating between two temperatures. It consists of four reversible processes: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression. The efficiency of the Carnot cycle is given by the expression:
Efficiency = 1 - (Tc/Th)
Where Tc is the absolute temperature of the cold reservoir and Th is the absolute temperature of the hot reservoir.
Explanation:
To understand why decreasing the lowest temperature (Tc) increases the efficiency of the Carnot cycle, let's consider the expression for efficiency:
Efficiency = 1 - (Tc/Th)
Effect of decreasing the lowest temperature:
When the lowest temperature (Tc) is decreased while keeping the highest temperature (Th) constant, the value of the term (Tc/Th) decreases. As a result, the efficiency of the Carnot cycle increases.
Reasoning:
There are two main reasons why decreasing the lowest temperature increases the efficiency of the Carnot cycle:
1. Increased temperature difference:
The efficiency of a heat engine is directly proportional to the temperature difference between the hot and cold reservoirs. By decreasing the lowest temperature (Tc), the temperature difference (Th - Tc) increases. This larger temperature difference allows for a greater conversion of heat into work, resulting in a higher efficiency.
2. Reduced heat loss:
Heat engines operate by extracting heat from the hot reservoir and rejecting heat to the cold reservoir. However, some heat is inevitably lost to the surroundings during this process. By decreasing the lowest temperature (Tc), the temperature difference between the heat engine and the surroundings also decreases, reducing the amount of heat lost. This reduction in heat loss contributes to an increase in efficiency.
Conclusion:
In conclusion, the efficiency of the Carnot cycle can be increased by decreasing the lowest temperature (Tc). This decrease results in a larger temperature difference between the hot and cold reservoirs, allowing for a greater conversion of heat into work. Additionally, reducing the lowest temperature helps to minimize heat loss to the surroundings, further improving the efficiency of the cycle.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer?
Question Description
The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer?.
The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The efficiency of the Carnot cycle may be increased by.Select one:a)increasing the lowest temperatureb)decreasing the highest temperaturec)Keeping the lowest temperature constantd)decreasing the lowest temperatureCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.













