Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Consider the sequence S0,S1,S2,....defined as...
Start Learning for Free
Consider the sequence S0,S1,S2,.... defined as follows: S0 = 0, S1 = 1 and Sn = 2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?
- a)for every n > 1, S2n is even
- b)for every n > 1, S2n+1 is odd
- c)for every n > 1, S3n is multiple of 3
- d)for every n > 1, S4n is multiple of 6
- e)none of the above
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 ...
Sn = 2Sn−1 + Sn−2
Characterstic polynomial for this recurrence is x2 = 2x + 1
x2 − 2x − 1 = 0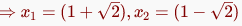 
The solution to the recurrence relation is of the form :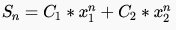
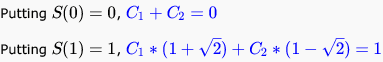
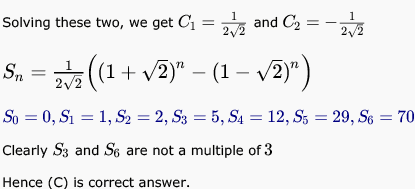
The solution to the recurrence relation is of the form :
Most Upvoted Answer
Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 ...
Explanation:
To determine which statements are true or false, we need to examine the given sequence and analyze the properties of the terms.
Sequence Definition:
The sequence is defined as follows:
- S0 = 0
- S1 = 1
- Sn = 2Sn-1 + Sn-2 for n ≥ 2
Statement a: for every n ≥ 1, S2n is even
To prove this statement, we need to show that S2n is always divisible by 2 for any positive value of n.
Proof by Induction:
Base Case:
For n = 1, S2 = S1 = 1, which is odd.
So, the base case is not divisible by 2.
Inductive Hypothesis:
Assume that for some positive integer k, S2k is divisible by 2.
Inductive Step:
We need to prove that S2(k+1) is divisible by 2.
S2(k+1) = 2S2k + S2(k-1)
Since S2k is divisible by 2 (as per our assumption), and S2(k-1) is also divisible by 2 (as per the inductive hypothesis), the sum of two even numbers is always even.
Therefore, S2(k+1) is divisible by 2.
By the principle of mathematical induction, we can conclude that for every n ≥ 1, S2n is even.
Statement b: for every n ≥ 1, S2n + 1 is odd
To prove this statement, we need to show that S2n + 1 is never divisible by 2 for any positive value of n.
Proof by Contradiction:
Assume that there exists some positive integer k for which S2k + 1 is divisible by 2.
This means S2k + 1 = 2m for some integer m.
Substituting the recursive definition of the sequence:
2S2(k-1) + S2(k-2) + 1 = 2m
2(S2(k-1) + S2(k-2)) + 1 = 2m
2(S2(k-1) + S2(k-2)) = 2m - 1
The left-hand side of the equation is even (as it is a multiple of 2), while the right-hand side is odd (as it is 1 less than a multiple of 2).
This leads to a contradiction, proving that S2k + 1 is never divisible by 2.
Therefore, for every n ≥ 1, S2n + 1 is odd.
Statement c: for every n ≥ 1, S3n is a multiple of 3
To prove this statement, we need to show that S3n is always divisible by 3 for any positive value of n.
Counterexample:
Let's consider n = 1:
S3(1) = S3 = 2S2 + S1 = 2(1) + 1 = 3
3 is not divisible by 3, so the statement is false.
Therefore, statement c is false.
To determine which statements are true or false, we need to examine the given sequence and analyze the properties of the terms.
Sequence Definition:
The sequence is defined as follows:
- S0 = 0
- S1 = 1
- Sn = 2Sn-1 + Sn-2 for n ≥ 2
Statement a: for every n ≥ 1, S2n is even
To prove this statement, we need to show that S2n is always divisible by 2 for any positive value of n.
Proof by Induction:
Base Case:
For n = 1, S2 = S1 = 1, which is odd.
So, the base case is not divisible by 2.
Inductive Hypothesis:
Assume that for some positive integer k, S2k is divisible by 2.
Inductive Step:
We need to prove that S2(k+1) is divisible by 2.
S2(k+1) = 2S2k + S2(k-1)
Since S2k is divisible by 2 (as per our assumption), and S2(k-1) is also divisible by 2 (as per the inductive hypothesis), the sum of two even numbers is always even.
Therefore, S2(k+1) is divisible by 2.
By the principle of mathematical induction, we can conclude that for every n ≥ 1, S2n is even.
Statement b: for every n ≥ 1, S2n + 1 is odd
To prove this statement, we need to show that S2n + 1 is never divisible by 2 for any positive value of n.
Proof by Contradiction:
Assume that there exists some positive integer k for which S2k + 1 is divisible by 2.
This means S2k + 1 = 2m for some integer m.
Substituting the recursive definition of the sequence:
2S2(k-1) + S2(k-2) + 1 = 2m
2(S2(k-1) + S2(k-2)) + 1 = 2m
2(S2(k-1) + S2(k-2)) = 2m - 1
The left-hand side of the equation is even (as it is a multiple of 2), while the right-hand side is odd (as it is 1 less than a multiple of 2).
This leads to a contradiction, proving that S2k + 1 is never divisible by 2.
Therefore, for every n ≥ 1, S2n + 1 is odd.
Statement c: for every n ≥ 1, S3n is a multiple of 3
To prove this statement, we need to show that S3n is always divisible by 3 for any positive value of n.
Counterexample:
Let's consider n = 1:
S3(1) = S3 = 2S2 + S1 = 2(1) + 1 = 3
3 is not divisible by 3, so the statement is false.
Therefore, statement c is false.
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Top Courses for Computer Science Engineering (CSE)View all
Question Description
Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer?.
Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the sequence S0,S1,S2,....defined as follows: S0 = 0, S1 = 1 and Sn =2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?a)for every n > 1, S2nis evenb)for every n > 1, S2n+1is oddc)for every n > 1, S3n is multiple of 3d)for every n > 1, S4n is multiple of 6e)none of the aboveCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.
|
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup