Physics Exam > Physics Questions > A beam of atoms moving in a certain direction...
Start Learning for Free
A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________
- a)1.3 x 105
- b)1.3 x 104
- c)2.1 x 103
- d)2.1 x 104
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A beam of atoms moving in a certain direction can be slowed down if th...
Photon momentum P = h/λ (for one cycle)
P must be equal to mV.
If n is no. of cycles then
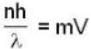
m = 23 x 1.66 x 10-27 kg = 3.818 x 10-26kg
V = 600 m/sec
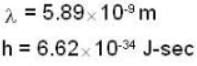
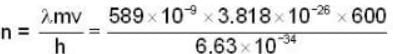
n = 2.1 x 104
P must be equal to mV.
If n is no. of cycles then
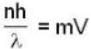
m = 23 x 1.66 x 10-27 kg = 3.818 x 10-26kg
V = 600 m/sec
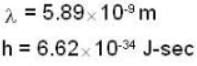
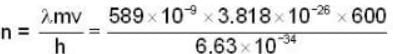
n = 2.1 x 104
Most Upvoted Answer
A beam of atoms moving in a certain direction can be slowed down if th...
Photon momentum P = h/λ (for one cycle)
P must be equal to mV.
If n is no. of cycles then
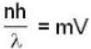
m = 23 x 1.66 x 10-27 kg = 3.818 x 10-26kg
V = 600 m/sec
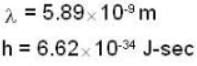
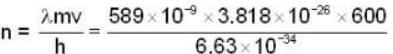
n = 2.1 x 104
P must be equal to mV.
If n is no. of cycles then
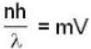
m = 23 x 1.66 x 10-27 kg = 3.818 x 10-26kg
V = 600 m/sec
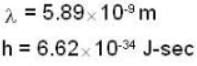
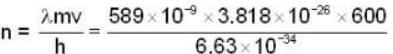
n = 2.1 x 104
Free Test
FREE
| Start Free Test |
Community Answer
A beam of atoms moving in a certain direction can be slowed down if th...
To bring a sodium atom to rest, we need to calculate the number of absorption and emission cycles required. Let's break down the problem step by step:
Given data:
- Mass number of sodium atom, A = 23
- Speed of sodium atom, v = 600 m/s
- Wavelength of laser beam, λ = 589 nm
1. Calculate the kinetic energy of the sodium atom:
The kinetic energy (K.E.) of a moving object is given by the formula:
K.E. = (1/2)mv^2
where m is the mass of the object and v is its velocity.
For a sodium atom with mass number A = 23, the mass (m) can be calculated by dividing the atomic mass by Avogadro's number:
m = (23 g/mol)/(6.022 x 10^23 atoms/mol) = 3.82 x 10^-23 g
Converting mass to kg:
m = 3.82 x 10^-26 kg
Now, substitute the values of m and v into the kinetic energy formula:
K.E. = (1/2)(3.82 x 10^-26 kg)(600 m/s)^2
K.E. = 6.89 x 10^-21 J
2. Calculate the energy of a photon with wavelength λ:
The energy (E) of a photon is given by the equation:
E = hc/λ
where h is Planck's constant (6.626 x 10^-34 J·s) and c is the speed of light (3.00 x 10^8 m/s).
Substitute the values of h, c, and λ into the equation:
E = (6.626 x 10^-34 J·s)(3.00 x 10^8 m/s)/(589 x 10^-9 m)
E = 3.37 x 10^-19 J
3. Calculate the number of absorption and emission cycles:
To bring the sodium atom to rest, the atom needs to absorb and emit photons until it loses all its kinetic energy. Each absorption and emission cycle transfers the energy of one photon (E) to the atom.
The number of cycles required can be calculated by dividing the initial kinetic energy (K.E.) by the energy of each photon (E):
Number of cycles = K.E./E
Number of cycles = (6.89 x 10^-21 J)/(3.37 x 10^-19 J)
Number of cycles ≈ 2.05 x 10^-2
However, the question asks for the approximate number of cycles. Rounding this value to the nearest integer, we get approximately 2.1 x 10^4 cycles.
Therefore, the correct answer is option D) 2.1 x 10^4.
Given data:
- Mass number of sodium atom, A = 23
- Speed of sodium atom, v = 600 m/s
- Wavelength of laser beam, λ = 589 nm
1. Calculate the kinetic energy of the sodium atom:
The kinetic energy (K.E.) of a moving object is given by the formula:
K.E. = (1/2)mv^2
where m is the mass of the object and v is its velocity.
For a sodium atom with mass number A = 23, the mass (m) can be calculated by dividing the atomic mass by Avogadro's number:
m = (23 g/mol)/(6.022 x 10^23 atoms/mol) = 3.82 x 10^-23 g
Converting mass to kg:
m = 3.82 x 10^-26 kg
Now, substitute the values of m and v into the kinetic energy formula:
K.E. = (1/2)(3.82 x 10^-26 kg)(600 m/s)^2
K.E. = 6.89 x 10^-21 J
2. Calculate the energy of a photon with wavelength λ:
The energy (E) of a photon is given by the equation:
E = hc/λ
where h is Planck's constant (6.626 x 10^-34 J·s) and c is the speed of light (3.00 x 10^8 m/s).
Substitute the values of h, c, and λ into the equation:
E = (6.626 x 10^-34 J·s)(3.00 x 10^8 m/s)/(589 x 10^-9 m)
E = 3.37 x 10^-19 J
3. Calculate the number of absorption and emission cycles:
To bring the sodium atom to rest, the atom needs to absorb and emit photons until it loses all its kinetic energy. Each absorption and emission cycle transfers the energy of one photon (E) to the atom.
The number of cycles required can be calculated by dividing the initial kinetic energy (K.E.) by the energy of each photon (E):
Number of cycles = K.E./E
Number of cycles = (6.89 x 10^-21 J)/(3.37 x 10^-19 J)
Number of cycles ≈ 2.05 x 10^-2
However, the question asks for the approximate number of cycles. Rounding this value to the nearest integer, we get approximately 2.1 x 10^4 cycles.
Therefore, the correct answer is option D) 2.1 x 10^4.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer?
Question Description
A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer?.
A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer?.
Solutions for A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A beam of atoms moving in a certain direction can be slowed down if they absorb photons from a laser beam moving in the opposite direction and subsequently spontaneously emit photons isotropically. For a beam of sodium atoms (mass number A = 23) with speed 600 m/sec. If a laser beam of wavelength 589 nm is used the number of such absorption and emission cycles needed to bring a sodium atom to rest would be approximately________a)1.3 x 105b)1.3 x 104c)2.1 x 103d)2.1 x 104Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















