Physics Exam > Physics Questions > A particle is initially in its ground state i...
Start Learning for Free
A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).
Correct answer is '5.7'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A particle is initially in its ground state in an infinite one - dimen...
When particle is initially in ground state. The state of the system is defined by
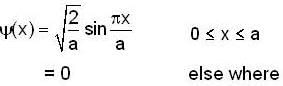
When the wall of the particle is moved to x = 3a the state of the system will remain same but eigenstates of the system will change Now, the eigenstates are defined by eigenfunction

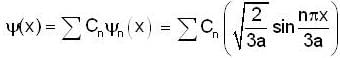
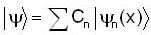
probability of finding the particle in ground state is given by
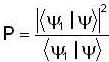
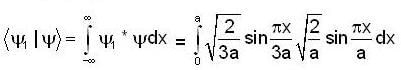
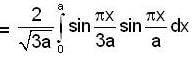
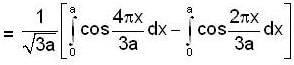
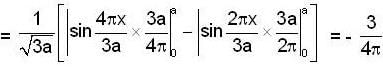
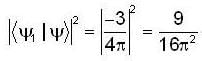
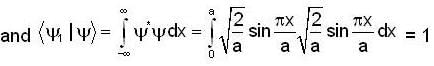
So, probability of finding the system in ground state is given by
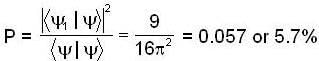
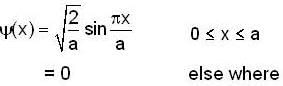
When the wall of the particle is moved to x = 3a the state of the system will remain same but eigenstates of the system will change Now, the eigenstates are defined by eigenfunction

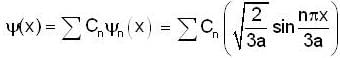
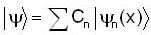
probability of finding the particle in ground state is given by
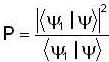
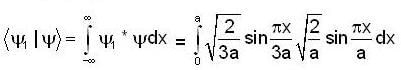
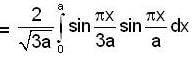
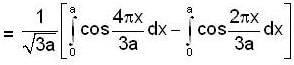
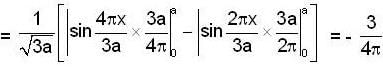
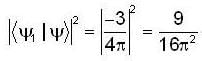
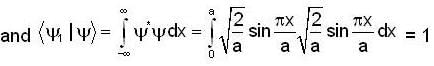
So, probability of finding the system in ground state is given by
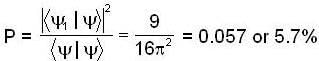
Most Upvoted Answer
A particle is initially in its ground state in an infinite one - dimen...
Introduction:
In this problem, we are given a particle initially in its ground state in an infinite one-dimensional potential box with sides at x = 0 and x = a. We are then asked to calculate the probability of finding the particle in the ground state of the new box when the wall at x = a is suddenly moved to x = 3a.
Understanding the problem:
To solve this problem, we need to calculate the probability of finding the particle in the ground state after the change in the potential box. The ground state wavefunction for an infinite one-dimensional potential box is given by:
ψ(x) = √(2/a) * sin(nπx/a)
Where n is the quantum number for the state of the particle and a is the length of the box.
Calculating the probability:
To calculate the probability of finding the particle in the ground state of the new box, we need to normalize the wavefunction and then find the probability density.
Normalizing the wavefunction:
To normalize the wavefunction, we need to calculate the normalization constant A:
∫|ψ(x)|² dx = 1
Integrating the modulus squared of the wavefunction gives:
∫(2/a) * sin²(nπx/a) dx = 1
Using the trigonometric identity sin²θ = (1/2)(1 - cos(2θ)), we can rewrite the integral as:
(2/a) * ∫(1/2)(1 - cos(2nπx/a)) dx = 1
Simplifying the integral, we have:
(1/a) * [(1/2)x - (a/4nπ)sin(2nπx/a)]|₀ᵃ = 1
Evaluating the integral at the limits of integration, we get:
(1/a) * [(1/2)a - (a/4nπ)sin(2nπa/a)] - (1/a) * [(1/2) * 0 - (a/4nπ)sin(2nπ * 0/a)] = 1
Simplifying further, we have:
(1/2) - (1/2nπ)sin(2nπ) = 1
The term sin(2nπ) is equal to zero since sin(2nπ) = sin(0) = 0. Therefore, the equation becomes:
(1/2) = 1
This implies that the normalization constant A is equal to √2.
Calculating the probability density:
To find the probability density, we need to calculate |ψ(x)|²:
|ψ(x)|² = (2/a) * sin²(nπx/a)
Substituting the value of the normalization constant A, we have:
|ψ(x)|² = (2/a) * sin²(nπx/a)
Since we are interested in the ground state (n = 1), the probability density becomes:
|ψ(x)|² = (2/a) * sin²(πx/a)
Calculating the probability:
To find the probability of finding the particle in the ground state of the new box, we need to integrate the probability density over the range x = a to x = 3
In this problem, we are given a particle initially in its ground state in an infinite one-dimensional potential box with sides at x = 0 and x = a. We are then asked to calculate the probability of finding the particle in the ground state of the new box when the wall at x = a is suddenly moved to x = 3a.
Understanding the problem:
To solve this problem, we need to calculate the probability of finding the particle in the ground state after the change in the potential box. The ground state wavefunction for an infinite one-dimensional potential box is given by:
ψ(x) = √(2/a) * sin(nπx/a)
Where n is the quantum number for the state of the particle and a is the length of the box.
Calculating the probability:
To calculate the probability of finding the particle in the ground state of the new box, we need to normalize the wavefunction and then find the probability density.
Normalizing the wavefunction:
To normalize the wavefunction, we need to calculate the normalization constant A:
∫|ψ(x)|² dx = 1
Integrating the modulus squared of the wavefunction gives:
∫(2/a) * sin²(nπx/a) dx = 1
Using the trigonometric identity sin²θ = (1/2)(1 - cos(2θ)), we can rewrite the integral as:
(2/a) * ∫(1/2)(1 - cos(2nπx/a)) dx = 1
Simplifying the integral, we have:
(1/a) * [(1/2)x - (a/4nπ)sin(2nπx/a)]|₀ᵃ = 1
Evaluating the integral at the limits of integration, we get:
(1/a) * [(1/2)a - (a/4nπ)sin(2nπa/a)] - (1/a) * [(1/2) * 0 - (a/4nπ)sin(2nπ * 0/a)] = 1
Simplifying further, we have:
(1/2) - (1/2nπ)sin(2nπ) = 1
The term sin(2nπ) is equal to zero since sin(2nπ) = sin(0) = 0. Therefore, the equation becomes:
(1/2) = 1
This implies that the normalization constant A is equal to √2.
Calculating the probability density:
To find the probability density, we need to calculate |ψ(x)|²:
|ψ(x)|² = (2/a) * sin²(nπx/a)
Substituting the value of the normalization constant A, we have:
|ψ(x)|² = (2/a) * sin²(nπx/a)
Since we are interested in the ground state (n = 1), the probability density becomes:
|ψ(x)|² = (2/a) * sin²(πx/a)
Calculating the probability:
To find the probability of finding the particle in the ground state of the new box, we need to integrate the probability density over the range x = a to x = 3

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer?
Question Description
A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer?.
A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer?.
Solutions for A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer?, a detailed solution for A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? has been provided alongside types of A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A particle is initially in its ground state in an infinite one - dimensional potential box with sides at x = 0 and x = a. If the wall of box at x = a is suddenly moved to x = 3a, calculate the probability of finding the particle in the ground state of the new box is ________(in percentage).Correct answer is '5.7'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















