Physics Exam > Physics Questions > One mole of an ideal gas whose adiabatic expo...
Start Learning for Free
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.
- a)-R (1 - α )ΔT
- b)-R (1 + α )ΔT
- c)R (1 -α )ΔT
- d)R (1 + α )ΔT
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
One mole of an ideal gas whose adiabatic exponent equals R undergoes a...
p = aTα
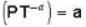


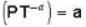


Most Upvoted Answer
One mole of an ideal gas whose adiabatic exponent equals R undergoes a...
To solve this problem, let's start with the ideal gas law:
PV = nRT
where:
P = pressure
V = volume
n = number of moles of gas
R = ideal gas constant
T = temperature
Since we're given that the gas pressure relates to the temperature as P = aT, we can substitute this into the ideal gas law equation:
(aT)V = nRT
Next, let's consider the adiabatic exponent, γ. For an ideal gas, γ is defined as the ratio of specific heat capacities:
γ = Cp/Cv
where:
Cp = specific heat capacity at constant pressure
Cv = specific heat capacity at constant volume
Since the gas is an ideal gas, γ is constant. Given that the adiabatic exponent equals R, we have:
γ = R
Now, let's consider an adiabatic process, where no heat is exchanged with the surroundings. In an adiabatic process, the relationship between pressure and volume is given by:
PV^γ = constant
Substituting the equation relating pressure to temperature, we have:
(aT)V^γ = constant
Since we are given that there is one mole of gas, we can substitute n = 1 into the ideal gas law equation:
(aT)V = RT
Rearranging this equation, we have:
V = RT/aT
Simplifying, we find:
V = R/a
So, in an adiabatic process, the volume of one mole of gas is directly proportional to the ideal gas constant divided by the constant of proportionality, a.
Note: The adiabatic exponent being equal to R is not a typical scenario for an ideal gas. Usually, γ takes on values between 1 and 2, depending on the gas.
PV = nRT
where:
P = pressure
V = volume
n = number of moles of gas
R = ideal gas constant
T = temperature
Since we're given that the gas pressure relates to the temperature as P = aT, we can substitute this into the ideal gas law equation:
(aT)V = nRT
Next, let's consider the adiabatic exponent, γ. For an ideal gas, γ is defined as the ratio of specific heat capacities:
γ = Cp/Cv
where:
Cp = specific heat capacity at constant pressure
Cv = specific heat capacity at constant volume
Since the gas is an ideal gas, γ is constant. Given that the adiabatic exponent equals R, we have:
γ = R
Now, let's consider an adiabatic process, where no heat is exchanged with the surroundings. In an adiabatic process, the relationship between pressure and volume is given by:
PV^γ = constant
Substituting the equation relating pressure to temperature, we have:
(aT)V^γ = constant
Since we are given that there is one mole of gas, we can substitute n = 1 into the ideal gas law equation:
(aT)V = RT
Rearranging this equation, we have:
V = RT/aT
Simplifying, we find:
V = R/a
So, in an adiabatic process, the volume of one mole of gas is directly proportional to the ideal gas constant divided by the constant of proportionality, a.
Note: The adiabatic exponent being equal to R is not a typical scenario for an ideal gas. Usually, γ takes on values between 1 and 2, depending on the gas.
Free Test
FREE
| Start Free Test |
Community Answer
One mole of an ideal gas whose adiabatic exponent equals R undergoes a...
p = aTα







|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer?
Question Description
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer?.
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer?.
Solutions for One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.a)-R (1 - α )ΔTb)-R (1 + α )ΔTc)R (1 -α )ΔTd)R (1 + α )ΔTCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















