Mechanical Engineering Exam > Mechanical Engineering Questions > A cantilever beam is deflected by δ due...
Start Learning for Free
A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:
- a)2
- b)1/2
- c)1/8
- d)8
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A cantilever beam is deflected by δ due to load P. If length of ...
Deflection of cantilever beam having concentrated load at the free end is given by
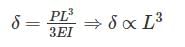
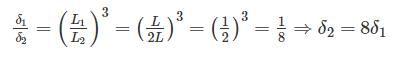
Most Upvoted Answer
A cantilever beam is deflected by δ due to load P. If length of ...
An applied load at the free end of the beam. The deflection of the beam is the displacement of the free end from its original position. The deflection of a cantilever beam can be calculated using various methods such as the double integration method, the moment-area method, or finite element analysis.
The deflection of a cantilever beam depends on several factors including the length of the beam, the material properties of the beam, the cross-sectional shape of the beam, and the magnitude and distribution of the applied load. In general, a longer beam will have a larger deflection than a shorter beam for the same applied load.
The material properties of the beam, such as its modulus of elasticity and moment of inertia, also affect the deflection. A stiffer material will have a smaller deflection than a more flexible material for the same applied load. The moment of inertia, which is a measure of the beam's resistance to bending, also plays a role in determining the deflection.
The cross-sectional shape of the beam can also influence the deflection. A beam with a larger moment of inertia will have a smaller deflection than a beam with a smaller moment of inertia for the same applied load. This is because a larger moment of inertia provides more resistance to bending.
The magnitude and distribution of the applied load on the beam also affect the deflection. A larger applied load will result in a larger deflection, while a more concentrated load will cause a larger deflection at the point of application.
Overall, the deflection of a cantilever beam is a complex problem that depends on several factors. Calculating the deflection requires knowledge of the beam's geometry, material properties, and the applied load.
The deflection of a cantilever beam depends on several factors including the length of the beam, the material properties of the beam, the cross-sectional shape of the beam, and the magnitude and distribution of the applied load. In general, a longer beam will have a larger deflection than a shorter beam for the same applied load.
The material properties of the beam, such as its modulus of elasticity and moment of inertia, also affect the deflection. A stiffer material will have a smaller deflection than a more flexible material for the same applied load. The moment of inertia, which is a measure of the beam's resistance to bending, also plays a role in determining the deflection.
The cross-sectional shape of the beam can also influence the deflection. A beam with a larger moment of inertia will have a smaller deflection than a beam with a smaller moment of inertia for the same applied load. This is because a larger moment of inertia provides more resistance to bending.
The magnitude and distribution of the applied load on the beam also affect the deflection. A larger applied load will result in a larger deflection, while a more concentrated load will cause a larger deflection at the point of application.
Overall, the deflection of a cantilever beam is a complex problem that depends on several factors. Calculating the deflection requires knowledge of the beam's geometry, material properties, and the applied load.

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer?.
A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer?.
Solutions for A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:a)2b)1/2c)1/8d)8Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















