Physics Exam > Physics Questions > Consider a beam of light of wavelength '&...
Start Learning for Free
Consider a beam of light of wavelength 'λ' incident on a system of a polarizer & an analyzer. The analyzer is oriented at 450 to the polarizer. When an optical component is introduced between them, the output intensity becomes zero. (Light is incident normally on all components).The optical component is:-
- a)a full wave plate
- b)a half-wave plate
- c)a quarter-wave plate
- d)an ordinary glass plate.
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider a beam of light of wavelength 'λ' incident on ...
When half-wave plate is introduced, the plane of polarization is rotated by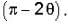 
Since intensity o f light analyzer is zero, plane o f polarization rotates by an angle 450.
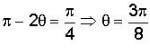
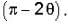Since intensity o f light analyzer is zero, plane o f polarization rotates by an angle 450.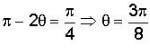Most Upvoted Answer
Consider a beam of light of wavelength 'λ' incident on ...
Λ = 500 nm (nanometers) passing through a narrow slit of width d = 0.1 mm (millimeters). The diffraction pattern produced by the slit can be analyzed using the principles of wave optics.
Diffraction occurs when a wave encounters an obstacle or aperture that is comparable in size to its wavelength. In this case, the wavelength of the light is 500 nm, which is in the visible range of the electromagnetic spectrum. The narrow slit has a width of 0.1 mm, which is larger than the wavelength of the light.
When light passes through a narrow slit, it spreads out and creates a diffraction pattern on a screen or surface placed behind the slit. This pattern consists of alternating bright and dark fringes, known as interference fringes.
The spacing between the fringes in the diffraction pattern can be calculated using the formula:
sin(θ) = mλ / d
Where:
- θ is the angle between the direction of the incident beam and the direction of the m-th order fringe.
- m is the order of the fringe (m = 0 for the central maximum, m = ±1 for the first-order fringes, m = ±2 for the second-order fringes, and so on).
- λ is the wavelength of the light.
- d is the width of the slit.
Using this formula, we can calculate the angle θ for the first-order fringe (m = ±1):
sin(θ) = (±1)(500 nm) / (0.1 mm)
θ = sin^(-1)(±1)(500 nm) / (0.1 mm)
The value of sin^(-1)(x) gives the angle whose sine is x. So we can solve this equation to find the value of θ.
Once we have the angle θ, we can calculate the spacing between the fringes using the formula:
dθ = λ / d
Where:
- dθ is the spacing between the fringes.
- λ is the wavelength of the light.
- d is the width of the slit.
Using the values given, we can substitute them into the formula to find the spacing between the fringes.
It's important to note that this calculation assumes the light is passing through a single narrow slit. If there are multiple slits or other factors affecting the diffraction pattern, the calculations may be more complex.
Diffraction occurs when a wave encounters an obstacle or aperture that is comparable in size to its wavelength. In this case, the wavelength of the light is 500 nm, which is in the visible range of the electromagnetic spectrum. The narrow slit has a width of 0.1 mm, which is larger than the wavelength of the light.
When light passes through a narrow slit, it spreads out and creates a diffraction pattern on a screen or surface placed behind the slit. This pattern consists of alternating bright and dark fringes, known as interference fringes.
The spacing between the fringes in the diffraction pattern can be calculated using the formula:
sin(θ) = mλ / d
Where:
- θ is the angle between the direction of the incident beam and the direction of the m-th order fringe.
- m is the order of the fringe (m = 0 for the central maximum, m = ±1 for the first-order fringes, m = ±2 for the second-order fringes, and so on).
- λ is the wavelength of the light.
- d is the width of the slit.
Using this formula, we can calculate the angle θ for the first-order fringe (m = ±1):
sin(θ) = (±1)(500 nm) / (0.1 mm)
θ = sin^(-1)(±1)(500 nm) / (0.1 mm)
The value of sin^(-1)(x) gives the angle whose sine is x. So we can solve this equation to find the value of θ.
Once we have the angle θ, we can calculate the spacing between the fringes using the formula:
dθ = λ / d
Where:
- dθ is the spacing between the fringes.
- λ is the wavelength of the light.
- d is the width of the slit.
Using the values given, we can substitute them into the formula to find the spacing between the fringes.
It's important to note that this calculation assumes the light is passing through a single narrow slit. If there are multiple slits or other factors affecting the diffraction pattern, the calculations may be more complex.
|
Explore Courses for Physics exam
|
|
Similar Physics Doubts
Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer?
Question Description
Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer?.
Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer?.
Solutions for Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a beam of light of wavelength 'λ' incident on a system of a polarizer &an analyzer. The analyzer is oriented at 450 to the polarizer. When an opticalcomponent is introduced between them, the output intensity becomes zero.(Light is incident normally on all components).The optical component is:-a)a full wave plateb)a half-wave platec)a quarter-wave plated)an ordinary glass plate.Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Physics tests.
|
|
Explore Courses for Physics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup