Mechanical Engineering Exam > Mechanical Engineering Questions > The ratio of long and short unit cell dimensi...
Start Learning for Free
The ratio of long and short unit cell dimensions of ideal HCP crystal structure should be
- a)1.56
- b)1.89
- c)1.633
- d)1.59
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
The ratio of long and short unit cell dimensions of ideal HCP crystal ...
For the ideal HCP packing, the ratio of c/a is 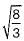 i.e. 1.633. The actual HCP metals deviate from ideal c/a ratio.
i.e. 1.633. The actual HCP metals deviate from ideal c/a ratio.
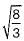 i.e. 1.633. The actual HCP metals deviate from ideal c/a ratio.
i.e. 1.633. The actual HCP metals deviate from ideal c/a ratio.Most Upvoted Answer
The ratio of long and short unit cell dimensions of ideal HCP crystal ...
The ideal crystal structure of a hexagonal close-packed (HCP) crystal consists of layers of atoms arranged in a hexagonal pattern. This crystal structure can be visualized as a stack of close-packed hexagonal layers, with each layer offset from the previous one by half of the interlayer spacing. In an HCP crystal, there are two types of lattice parameters: the long unit cell dimension, denoted as "c", and the short unit cell dimensions, denoted as "a".
Explanation:
1. HCP Crystal Structure:
- The HCP crystal structure is one of the most common crystal structures in nature and is found in many metals and alloys, such as titanium and magnesium.
- In an HCP crystal, the atoms are arranged in a close-packed hexagonal lattice, with each atom surrounded by six nearest neighbors forming an equilateral triangle.
- The layers of atoms in an HCP crystal are stacked in an ABAB... pattern, where each A layer is directly above a B layer. This stacking sequence results in a hexagonal unit cell.
2. Lattice Parameters:
- In an HCP crystal, the long unit cell dimension "c" is the distance between two adjacent layers along the vertical direction. It is also equal to the height of the unit cell.
- The short unit cell dimensions "a" are the distances between neighboring atoms within a layer. These dimensions are equal to the side lengths of the hexagonal unit cell.
3. Relationship between c and a:
- The ratio between the long and short unit cell dimensions of an ideal HCP crystal can be determined using trigonometry.
- In an HCP crystal, the hexagonal unit cell can be visualized as two interpenetrating triangular lattices. The distance between adjacent atoms within a layer (a) can be related to the height of the unit cell (c) using the trigonometric relationship: c = 2 * a * sqrt(6) / 3.
- Solving this equation for the ratio c/a gives: c/a = sqrt(8/3) ≈ 1.633.
4. Determining the Correct Answer:
- Comparing the given options, we can see that the correct answer is option 'C', which is approximately equal to 1.633.
- This ratio represents the ideal relationship between the long and short unit cell dimensions in an HCP crystal structure.
In summary, the ratio of long and short unit cell dimensions in an ideal HCP crystal structure is approximately 1.633. This ratio is derived from the trigonometric relationship between the height of the unit cell and the distance between neighboring atoms within a layer.
Explanation:
1. HCP Crystal Structure:
- The HCP crystal structure is one of the most common crystal structures in nature and is found in many metals and alloys, such as titanium and magnesium.
- In an HCP crystal, the atoms are arranged in a close-packed hexagonal lattice, with each atom surrounded by six nearest neighbors forming an equilateral triangle.
- The layers of atoms in an HCP crystal are stacked in an ABAB... pattern, where each A layer is directly above a B layer. This stacking sequence results in a hexagonal unit cell.
2. Lattice Parameters:
- In an HCP crystal, the long unit cell dimension "c" is the distance between two adjacent layers along the vertical direction. It is also equal to the height of the unit cell.
- The short unit cell dimensions "a" are the distances between neighboring atoms within a layer. These dimensions are equal to the side lengths of the hexagonal unit cell.
3. Relationship between c and a:
- The ratio between the long and short unit cell dimensions of an ideal HCP crystal can be determined using trigonometry.
- In an HCP crystal, the hexagonal unit cell can be visualized as two interpenetrating triangular lattices. The distance between adjacent atoms within a layer (a) can be related to the height of the unit cell (c) using the trigonometric relationship: c = 2 * a * sqrt(6) / 3.
- Solving this equation for the ratio c/a gives: c/a = sqrt(8/3) ≈ 1.633.
4. Determining the Correct Answer:
- Comparing the given options, we can see that the correct answer is option 'C', which is approximately equal to 1.633.
- This ratio represents the ideal relationship between the long and short unit cell dimensions in an HCP crystal structure.
In summary, the ratio of long and short unit cell dimensions in an ideal HCP crystal structure is approximately 1.633. This ratio is derived from the trigonometric relationship between the height of the unit cell and the distance between neighboring atoms within a layer.

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer?.
The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer?.
Solutions for The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The ratio of long and short unit cell dimensions of ideal HCP crystal structure should bea)1.56b)1.89c)1.633d)1.59Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























