Mathematics Exam > Mathematics Questions > How many arbitrary constants are there in the...
Start Learning for Free
How many arbitrary constants are there in the equation of a plane?
- a)2
- b)3
- c)4
- d)any finite number
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
How many arbitrary constants are there in the equation of a plane?a)2b...
The general equation of first degree in x, y, z namely
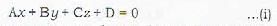
represents a plane, where at least one of A, B and C is non-zero.
Remark: 1. Let A ≠ 0. Then equation (i)
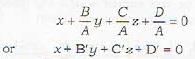
Therefore the general equation of a plane involves three independent (essential) arbitrary constant.
Hence if three independent conditions are given then the plane can be determined completely.
Remark : 2. If D = 0 then the plane will pass through the origin.
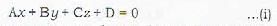
represents a plane, where at least one of A, B and C is non-zero.
Remark: 1. Let A ≠ 0. Then equation (i)
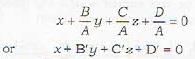
Therefore the general equation of a plane involves three independent (essential) arbitrary constant.
Hence if three independent conditions are given then the plane can be determined completely.
Remark : 2. If D = 0 then the plane will pass through the origin.
Most Upvoted Answer
How many arbitrary constants are there in the equation of a plane?a)2b...
Arbitrary Constants in the Equation of a Plane
In mathematics, the equation of a plane is typically given in the form Ax + By + Cz + D = 0, where A, B, and C are the coefficients of x, y, and z respectively, and D is a constant. The coefficients A, B, and C determine the direction of the plane's normal vector, while the constant D determines the distance of the plane from the origin.
To determine the number of arbitrary constants in the equation of a plane, we need to consider the number of independent variables or parameters involved.
Variables and Parameters
In the equation of a plane, the variables are x, y, and z, which represent the coordinates of any point on the plane. These variables can take any real values.
On the other hand, the parameters or constants A, B, C, and D are fixed values that determine the characteristics of the plane. They are not variables and cannot take arbitrary values.
Degrees of Freedom
The degrees of freedom of a system refer to the number of independent variables or parameters that can be chosen freely. In the case of a plane, the degrees of freedom represent the number of parameters that can be varied without affecting the plane's essential characteristics.
In the equation of a plane, there are four parameters: A, B, C, and D. However, these parameters are not all independent of each other. The equation is homogeneous, meaning that if we scale all the parameters by a constant factor, the equation remains the same. This implies that three out of the four parameters are dependent.
Equation with Arbitrary Constants
We can rewrite the equation of a plane as follows:
Ax + By + Cz + D = 0
Dividing the equation by D, we get:
(A/D)x + (B/D)y + (C/D)z + 1 = 0
Letting p = A/D, q = B/D, and r = C/D, the equation becomes:
px + qy + rz + 1 = 0
In this form, the equation of the plane has three arbitrary constants: p, q, and r. These constants can take any real values, and they determine the direction and distance of the plane.
Therefore, the correct answer is option 'B' - there are three arbitrary constants in the equation of a plane.
In mathematics, the equation of a plane is typically given in the form Ax + By + Cz + D = 0, where A, B, and C are the coefficients of x, y, and z respectively, and D is a constant. The coefficients A, B, and C determine the direction of the plane's normal vector, while the constant D determines the distance of the plane from the origin.
To determine the number of arbitrary constants in the equation of a plane, we need to consider the number of independent variables or parameters involved.
Variables and Parameters
In the equation of a plane, the variables are x, y, and z, which represent the coordinates of any point on the plane. These variables can take any real values.
On the other hand, the parameters or constants A, B, C, and D are fixed values that determine the characteristics of the plane. They are not variables and cannot take arbitrary values.
Degrees of Freedom
The degrees of freedom of a system refer to the number of independent variables or parameters that can be chosen freely. In the case of a plane, the degrees of freedom represent the number of parameters that can be varied without affecting the plane's essential characteristics.
In the equation of a plane, there are four parameters: A, B, C, and D. However, these parameters are not all independent of each other. The equation is homogeneous, meaning that if we scale all the parameters by a constant factor, the equation remains the same. This implies that three out of the four parameters are dependent.
Equation with Arbitrary Constants
We can rewrite the equation of a plane as follows:
Ax + By + Cz + D = 0
Dividing the equation by D, we get:
(A/D)x + (B/D)y + (C/D)z + 1 = 0
Letting p = A/D, q = B/D, and r = C/D, the equation becomes:
px + qy + rz + 1 = 0
In this form, the equation of the plane has three arbitrary constants: p, q, and r. These constants can take any real values, and they determine the direction and distance of the plane.
Therefore, the correct answer is option 'B' - there are three arbitrary constants in the equation of a plane.
|
Explore Courses for Mathematics exam
|
|
Similar Mathematics Doubts
How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer?
Question Description
How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer?.
How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer?.
Solutions for How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice How many arbitrary constants are there in the equation of a plane?a)2b)3c)4d)any finite numberCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Mathematics tests.
|
|
Explore Courses for Mathematics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup