Physics Exam > Physics Questions > A wide cylindrical vessel 50 cm in height is ...
Start Learning for Free
A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.
Correct answer is '25'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A wide cylindrical vessel 50 cm in height is filled with water and res...
Let H be the total height of the water column and the hole is made at a height h from the bottom
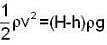
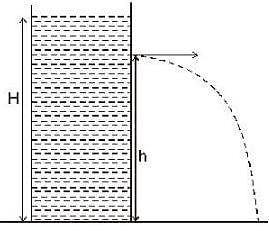
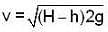
for the horizontal range
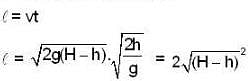
Now for maximum l

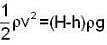

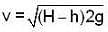
for the horizontal range
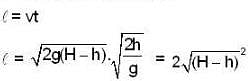
Now for maximum l

Most Upvoted Answer
A wide cylindrical vessel 50 cm in height is filled with water and res...
Problem Analysis
To solve this problem, we need to consider the concept of projectile motion. The water jet coming out of the hole will follow a parabolic trajectory, and we want to find the height at which the hole should be perforated so that the water jet hits the surface of the table at the maximum distance.
Key Information
- Height of the cylindrical vessel: 50 cm
- Viscosity of water: negligible
- Desired maximum distance from the vessel to the point where the water jet hits the table: lmax
Solution
To find the height at which the hole should be perforated, we can use the principles of projectile motion. The key idea is that the horizontal and vertical components of motion are independent of each other.
Step 1: Analyzing the Horizontal Motion
In the absence of air resistance, the horizontal component of the water jet's velocity remains constant throughout its motion. Therefore, the time taken for the water jet to hit the table is the same as the time taken for the water jet to fall vertically from the height of the hole to the table.
Step 2: Analyzing the Vertical Motion
Using the equations of motion, we can determine the time taken for the water jet to fall from the hole to the table. The equation for the vertical displacement is given by:
h = u*t + (1/2)*g*t^2,
where h is the height of the hole from the bottom of the vessel, u is the initial vertical velocity of the water jet (which is zero in this case), g is the acceleration due to gravity (approximately 9.8 m/s^2), and t is the time taken for the water jet to hit the table.
Step 3: Finding the Maximum Distance
To find the height at which the water jet should be perforated for maximum distance, we need to maximize the horizontal displacement. The horizontal displacement is given by:
lmax = v*t,
where v is the horizontal velocity of the water jet. Since the horizontal velocity remains constant, maximizing lmax is equivalent to maximizing t.
Step 4: Maximizing t
To maximize t, we need to find the value of h that maximizes the time taken for the water jet to fall from the hole to the table. This can be done by differentiating the equation for h with respect to t and setting the derivative equal to zero. Solving this equation will give us the value of h at which t is maximized.
Step 5: Calculating the Height
By solving the equation obtained in step 4, we find that the height at which the hole should be perforated for the water jet to hit the table at the maximum distance is h = 25 cm.
Therefore, the correct answer is 25 cm.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer?
Question Description
A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer?.
A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer?.
Solutions for A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer?, a detailed solution for A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? has been provided alongside types of A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A wide cylindrical vessel 50 cm in height is filled with water and rests on a table Assuming the viscosity to be negligible. Find at what height (in cm) from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax Cmaxfrorn the vessel.Correct answer is '25'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















