Mechanical Engineering Exam > Mechanical Engineering Questions > Consider a single server queuing model with P...
Start Learning for Free
Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue is
- a)1/11
- b)1/10
- c)1/9
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Consider a single server queuing model with Poisson arrivals (λ...

Probability that a person who comes in leaves without joining the queue i.e.
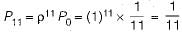
Most Upvoted Answer
Consider a single server queuing model with Poisson arrivals (λ...
Exponentially distributed interarrival times) and exponential service times. In this model, customers arrive at a rate of λ (mean interarrival time 1/λ) and are served at a rate of μ (mean service time 1/μ).
The behavior of this queuing system can be analyzed using the following parameters:
- λ: arrival rate (customers per unit time)
- μ: service rate (customers per unit time)
- ρ: traffic intensity (λ/μ)
- L: average number of customers in the system
- Lq: average number of customers in the queue
- W: average time a customer spends in the system
- Wq: average time a customer spends in the queue
To calculate these parameters, we can use the following formulas:
- ρ = λ/μ
- L = λ/(μ - λ)
- Lq = ρ^2/(1 - ρ)
- W = 1/(μ - λ)
- Wq = ρ/(μ - λ)
Note that these formulas assume that the system is stable, i.e., ρ < 1.="" if="" ρ="" ≥="" 1,="" the="" queue="" will="" become="" infinitely="" long="" and="" the="" system="" will="" not="" be="" able="" to="" handle="" the="" arrival="" />
These formulas provide insights into the behavior of the queuing system. For example, if ρ is high (close to 1), the system is heavily loaded and the queue is likely to be long. Conversely, if ρ is low (close to 0), the system is underutilized and there may be idle time for the server.
It is important to note that these formulas are based on certain assumptions, such as exponential interarrival and service times, and a single server. If these assumptions do not hold, more complex queuing models may be required to accurately analyze the system.
The behavior of this queuing system can be analyzed using the following parameters:
- λ: arrival rate (customers per unit time)
- μ: service rate (customers per unit time)
- ρ: traffic intensity (λ/μ)
- L: average number of customers in the system
- Lq: average number of customers in the queue
- W: average time a customer spends in the system
- Wq: average time a customer spends in the queue
To calculate these parameters, we can use the following formulas:
- ρ = λ/μ
- L = λ/(μ - λ)
- Lq = ρ^2/(1 - ρ)
- W = 1/(μ - λ)
- Wq = ρ/(μ - λ)
Note that these formulas assume that the system is stable, i.e., ρ < 1.="" if="" ρ="" ≥="" 1,="" the="" queue="" will="" become="" infinitely="" long="" and="" the="" system="" will="" not="" be="" able="" to="" handle="" the="" arrival="" />
These formulas provide insights into the behavior of the queuing system. For example, if ρ is high (close to 1), the system is heavily loaded and the queue is likely to be long. Conversely, if ρ is low (close to 0), the system is underutilized and there may be idle time for the server.
It is important to note that these formulas are based on certain assumptions, such as exponential interarrival and service times, and a single server. If these assumptions do not hold, more complex queuing models may be required to accurately analyze the system.

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer?.
Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer?.
Solutions for Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a single server queuing model with Poisson arrivals (λ = 4/hour) and exponential service (μ = 4/hour). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue isa)1/11b)1/10c)1/9d)1/2Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















